改进的基于地层损失概念的地表沉降经验预测方法

阎 飞

(北京京能地质工程有限公司，北京 102300)

0 引言

地层损失概念最早是Peck[1]在预测隧道开挖诱发地表沉降变形的研究中提出，其认为地层变形是由地层损失引起，从而假定地表沉降槽体的体积等于地层损失的体积。基坑开挖过程中，围护结构内外侧土压力平衡被打破，围护结构在内外压力差的作用下向坑内移动，从而引起坑周地表沉降。

如何根据围护结构的变形预测地表沉降一直是工程界的重要研究课题。地层损失的方法是由围护结构变形预测地表沉降的重要方法。目前，诸多学者根据地层损失概念，通过一系列合理假设，借助工程实际经验，由围护结构发生水平变形产生的侧移面积与地表发生下沉产生的沉降面积之间的相关性，计算地表沉降。侯学渊[2]参考盾构隧道施工诱发地表沉降的Peck和Schimidt公式，借鉴三角形沉降计算公式的推导思路，给出了利用地层损失概念计算指数型(即凹槽型)地表沉降曲线的求解过程。唐孟雄等[3，4]以凹槽形地表沉降为研究对象，提出采用正态分布函数描述地表沉降曲线。张尚根等[5-8]假设地表沉降影响范围为1.5倍的围护结构长度，围护结构水平变形最大值与地表沉降最大值之间存在一定关系，在这样假设的基础上进行地表沉降曲线预测。

综合现有的地层损失法的研究成果可以看出[9]，基坑地层损失法在计算地表沉降的过程中主要包含3方面内容：① 地表沉降面积计算；② 围护结构侧移面积计算；③ 地表沉降面积与围护结构侧移面积之间比值的确定。地表沉降面积通常根据假设地表沉降曲线函数(未知参数一般包含地表沉降最大值wmax，地表沉降最大值位置xm，地表沉降影响范围x0)，通过定积分运算得到；围护结构侧移面积可通过对工程实测围护结构水平变形曲线进行积分运算得到；地表沉降面积与围护结构侧移面积之比可由工程经验确定。其中，最主要的工作是确定地表沉降影响范围x0，计算地表沉降最大值wmax和地表沉降最大值位置xm。

确定x0、wmax和xm的值，总体上可以采用两种路径。先确定xm和x0，再计算wmax；或者先确定wmax和x0，再计算xm。然而，无论采用哪种计算路径，均需根据地区工程经验确定地表沉降影响范围x0，但不同地区地表沉降影响范围不同[5，7-8，10-12]，即使同一地区通过统计分析所确定的地表沉降影响范围也可能因为统计样本不同而有所差异[13-15]，因此实际工程中不易确定地表沉降影响范围x0。若地表沉降影响范围x0取值不当，将极易高估或者低估地表沉降，选择与地表沉降最大值位置xm相协调的地表沉降影响范围x0至关重要。

此外，上述计算路径在确定地表沉降最大值位置xm时，一般认为其仅与基坑开挖深度和土体力学参数内摩擦角有关[3-4]，而与其他因素无关，这显然与实际情况是不符的。已有研究表明[9]地表沉降最大值位置与围护结构水平变形曲线形态密切相关，因而地质条件类似，而地表沉降最大值位置不同，可能是由于围护结构水平变形曲线不同所致。选择先确定地表沉降最大值wmax和地表沉降影响范围x0，再计算地表沉降最大值位置xm这条计算路径时，易出现xm多解问题[5]。

为解决沉降最大值位置xm与地表沉降影响范围x0的协调性问题以及xm多解问题，本文基于前人研究成果，通过理论分析提出了一种改进的基于地层损失概念的地表沉降经验预测方法。

1 改进的地表沉降预测方法

在既有研究的基础之上，对凹槽型地表沉降进行分析。首先，视墙后地表沉降曲线服从正态分布；其次，通过分析围护结构的水平变形情况，并借助地表沉降显式解析表达式，进一步求解地表沉降最大值的位置坐标，记为xm；通过借助主、次要影响区分界点并假设沉降函数，进一步求解地表沉降影响范围x0；再次，利用上述步骤中得到的xm和x0，进一步对沉降曲线函数表达式进行积分，求出地表沉降曲线包络面积Av；然后求解出围护结构侧移面积Ah；最终利用Av与Ah计算求出地表沉降最大值wmax。依据wmax，结合假设函数就能对墙后任意处地表沉降进行定量预估。

1.1 地表沉降曲线函数假设

深基坑首道支撑一般采用钢筋混凝土支撑，由于围护结构顶部会承受一定程度的侧向约束，围护结构水平曲线在深基坑开挖完成后变形多呈现鼓胀变形，基坑附近则往往呈现出“凹槽型”的地表沉降曲线。在既有研究[3-7，8，11]的基础之上对该类型地表沉降曲线进行进一步的研究，假设墙后地表沉降曲线服从正态分布，可得：

(1)

相对应的曲线见图1。x为墙后任意位置距基坑边缘的水平距离；wmax为深基坑开挖过程中地表沉降最大值；xm为基坑边缘至地表沉降最大值间的水平距离；r=x0-xm，r为基坑开挖过程中沉降盆的影响半径，x0为基坑开挖过程中地表沉降所影响的范围。

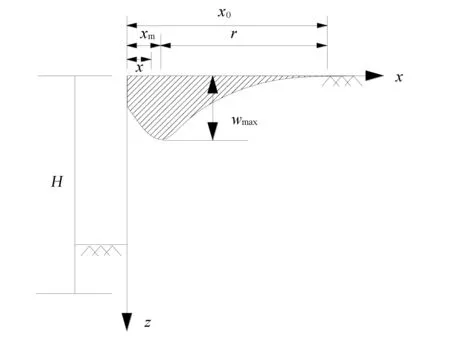
图1 基坑开挖引起的凹槽型地表沉降Fig.1 Fluted surface subsidence caused by foundation pit excavation

1.2 地表沉降最大值位置计算

胡之锋等人基于围护结构平移变形条件下的解析表达式，运用微积分思想，得出了围护结构在任意变形模式下的地表沉降显式解析解，通过与工程实测数据对比发现，该显式解析解得出的地表沉降最大值位置与实测值较为吻合[9]。因此，本文基于该地表沉降显式解析解，根据围护结构水平变形，计算地表沉降最大值位置xm。

胡之锋等人所采用的地表沉降显式解析解为

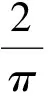
C5x2+C6x+C7)

(2)

其中，系数为

(3a)

(3b)

(3c)

(3d)

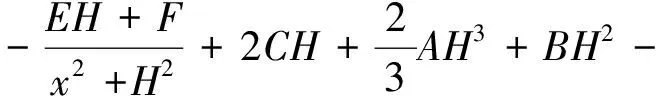
(3e)

(3f)

C7=F

(3g)

其中，H表示围护结构长度，A、B、C、D、E、F为多项式系数，可采用五次多项式表示围护结构水平位移：

f(h)=Ah5+Bh4+Ch3+Dh2+Eh+F

(4)

h表示计算点的深度。在得到式(2)表达式的情况下，以x为变量，对其求导，令其导数为零，可以得出地表沉降最大值位置xm。

1.3 地表沉降影响范围计算

基坑开挖过程中的地表沉降进行计算可借助地层损失理论，但此时x0的取值应处于合理区间，才能对地表沉降进行较为准确地计算。这是因为运用地层损失理论进行相关计算时最重要的两个计算参数为围护结构侧移面积Ah以及基坑开挖过程中的地表沉降面积Av，而这两者之间存在一定的比例关系。因此当Ah一定时，Av也就确定。此时一旦x0取值太小，通过计算后地表沉降曲线就会显著变短，而基坑主要响范围内曲线则会变得很陡，最终导致地表实际沉降值被高估；反之亦然。

在对既有研究[10，14，16]进一步分析后得知，尽管地表沉降影响范围因基坑工程的不同而略显差异，但主、次要影响区分界点的位置则呈现出相对一致的规律：位于墙后两倍基坑开挖深度处，大小约为0.1wmax，见图2。本文为了更准确地预测地表沉降，重点研究主、次要影响区分界点，并结合上节所求出的各特殊点间内在联系来计算地表沉降影响范围x0，使其与待求解的xm协调，最终对坑后地表沉降进行准确的估算。

图2 主次要影响区分界Fig.2 Division of primary and secondary influence areas

首先将主、次要影响区分界点坐标(2He，0.1wmax)代入式(1)可得：

(5)

由图3可见，地表沉降曲线中涉及的位置关系为

xm+xp=2He

(6)

图3 地表沉降影响范围求解示意图Fig.3 Schematic diagram for solution of influence range of surface subsidence

式(6)中xp为地表最大值沉降点距主、次要影响区分界点之间水平方向的距离。借助式(5)、式(6)得出：

xp=0.856r

(7)

根据r=x0-xm，结合式(6)、式(7)可得：

0.144xm+0.856x0=2He

(8)

在式(8)中代入地表沉降最大值位置xm以及基坑开挖深度He就能进一步对基坑开挖过程中的实际影响范围x0进行求解。

1.4 地表沉降曲线包络面积计算

求解出xm以及x0之后，对假设地表沉降曲线函数进行积分，能够得出地表沉降曲线包络面积Av，而Av是仅含wmax一个未知数的表达式。此处为了简化运算将地表沉降最大值位置设为坐标原点，也即假设xd=x-xm，于是求解出Av积分表达式如下所示：

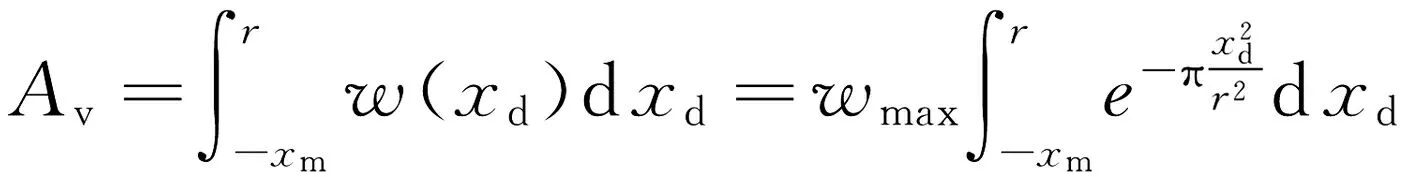
(9a)

经过变换后可得：

(9b)

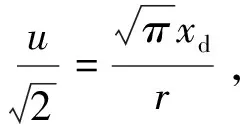
(9c)

Av=wmaxr[Φ(ur)-1+Φ(uxm)]

(9d)

式(9d)中，Φ(u)为标准正态分布函数，把ur代入可得

(10)

则式(9d)转化为

(9e)

根据求解得到的xm和x0，且已知r=x0-xm，r也为已知量，从而wmax为式(9e)中唯一未知数。

1.5 围护结构侧移面积计算

计算围护结构侧移面积Ah。首先，根据实测数据确定围护结构的水平位移，并拟合出水平位移表达式；然后，以围护结构长度范围为积分区间对拟合函数进行积分运算，求解出Ah。采用多项式对围护结构水平位移曲线进行拟合是当前较为常见的处理方式，研究[9]表明采用五次多项式进行拟合效果较好，因此本文对五次多项式进行拟合最终得出Ah。

如图3所示，设维护结构顶端为坐标原点，f(h)为对围护结构水平位移曲线进行拟合的五次多项式函数，可得Ah为

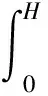
(11)

结合式(4)，对式(11)进行积分可得：

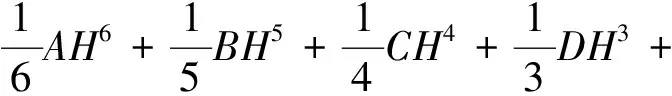
(12)

1.6 地表沉降最大值计算

围护结构侧移面积Ah可由式(12)通过计算得出，并结合Av、Ah以及前文已经推导出的Av表达式(9e)，就能对地表沉降最大值wmax进行求解。其中，Av、Ah的关系由CA给出，CA定义为

(13)

通过上述计算得出地表沉降最大值wmax，然后式(1)中代入wmax、xm和r就能得出地表沉降预测曲线。地表沉降预测曲线确定后就能非常方便地对墙后任意地表位置沉降值进行估算。

2 改进方法计算流程

综上，采用改进方法计算地表沉降的基本流程见图4，具体如下：

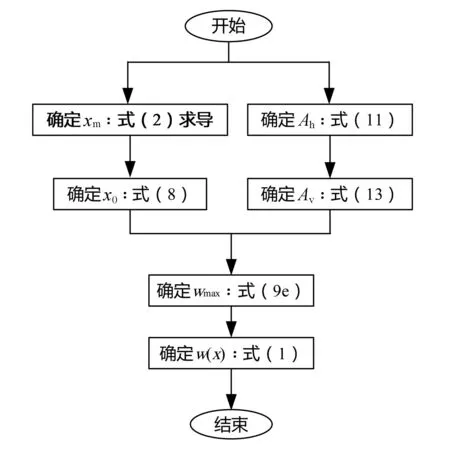
图4 改进方法计算地表沉降的流程Fig.4 The procedure of improved method to calculate surface subsidence

1)根据地表沉降的显式解析式(2)求导，令其导数为零，得出地表沉降最大值位置xm。

2)根据假设沉降曲线，基于相对较为稳定的主次要影响区分界点，根据式(8)利用地表沉降最大值位置xm计算地表沉降影响范围x0。

3)依据Av与Ah之间的关系式、围护结构水平位移的实测数据，并由式(11)求解出Ah，最终对地表沉降曲线包络面积Av进行求解。

4)借助式(9e)对地表沉降最大值wmax进行求解，然后在假设函数式(1)中代入wmax，就能对墙后任意地表位置的沉降值进行估算。

3 工程实例验证及分析

3.1 工程实例

本文主要选取台北软土TNEC基坑[17]、伦敦软土基坑[18-19]加以分析。具体的基坑的地层资料及开挖情况可以参考相应文献。这两个工程实测的围护结构水平位移及五次函数拟合曲线见图5a。

得出水平位移拟合曲线后，按照图4所示的流程可以得到地表沉降曲线(图5b)，计算的主要计算结果见表1。由图5中的地表沉降预测结果和实测结果对比可以看出，改进后的沉降计算方法具有较强的预测能力，完全可以满足工程实践要求。

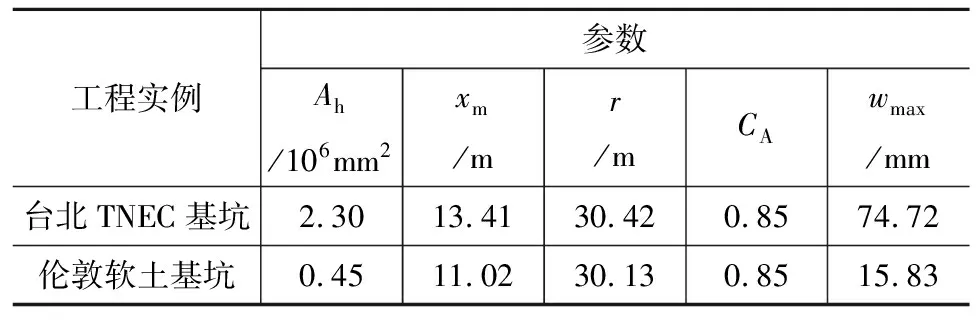
表1 主要计算结果Table 1 List of the main calculation result

图5 改进方法的工程实例应用

4 地表沉降影响范围的大小对地表沉降的影响分析

不同学者根据经验所得的地表沉降影响范围x0会有所不同。当先确定地表沉降最大值位置xm和地表沉降影响范围x0，再计算地表沉降最大值wmax时，如地表沉降影响范围x0取值不当，将极易高估或者低

估地表沉降。因此选择与地表沉降最大值位置xm相协调的地表沉降影响范围x0至关重要。

为了说明本文计算地表沉降影响范围x0方法的合理性，基于上述2个工程实例，分别计算x0为4He，2.5He，1.5He时的地表沉降预测曲线，并将其与采用改进方法得到的地表沉降曲线和实测数据进行对比。

图6给出了实测地表沉降曲线，以及取地表沉降影响范围x0分别为4He，2.5He，1.5He时采用改进方法得到的沉降曲线。由图6可见，xm不变的情况下，影响范围x0的取值越大，相应得出的曲线越平，总体沉降偏小；反之，曲线越陡，计算所得主要影响区内的地表沉降值偏大，这与前文分析一致，说明地表沉降影响范围x0取值不当会对地表沉降的计算结果产生重要影响。

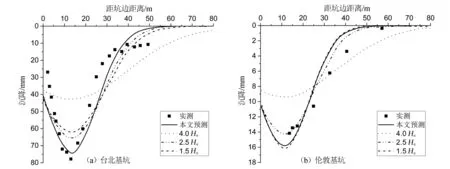
图6 地表沉降影响范围大小分析图Fig.6 Analysis chart of influence range of surface subsidence

改进的计算方法得到的地表沉降曲线与x0分别取4He，2.5He，1.5He时算得的地表沉降曲线相比，前者与实测数据更为吻合。这说明本文所采用的基于主次影响区分界计算x0较为合理，可避免传统经验法确定x0的不足，保证x0与xm之间的协调。

5 地表沉降最大值位置多解对地表沉降的影响分析

如前所述，传统方法中xm存在多解问题，为了避免该问题，基于上述两个工程实例，假设地表沉降最大值为围护结构水平位移最大值的62.5%[12，20]，从而根据围护结构水平位移最大值确定地表沉降最大值wmax。假设地表沉降影响范围x0为2.5He，便可反求地表沉降最大值位置xm。这两个工程实例最终计算的地表沉降最大值位置xm见表2。

表2 依据地表沉降最大值计算地表沉降Table 2 The surface settlement is calculated according to the maximum value of surface settlement

根据表2中的参数，图7给出了两个工程实例在不同地表沉降最大值位置xm时的地表沉降曲线，同时绘制出了采用本文方法计算得到的地表沉降曲线，以及实测地表沉降曲线。由图7可见，先算wmax与x0，再算xm时得到的地表沉降曲线与实测值相差较大，这是由于地表沉降影响范围x0，地表沉降最大值与围护结构水平变形最大值之间的数量关系都是根据工程经验确定，存在一定的不确定性。

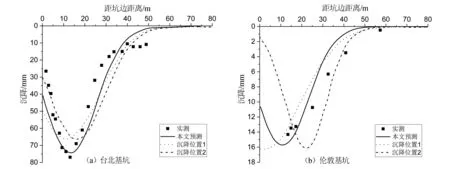
图7 地表沉降最大值位置多解分析图Fig.7 Multi-solution analysis diagram of the location of maximum surface subsidence

此外，当地表沉降最大值wmax，地表沉降影响范围x0确定时，存在多条地表沉降曲线，使得其曲线包络面积等于确定的地表沉降面积Av，从而造成地表沉降最大值位置xm存在多个解，不易取舍。说明本文采用先确定xm与x0，然后计算wmax这条计算路径具有一定的优越性。

6 结论

本文基于地表沉降曲线正态分布假设，提出了一种与围护结构水平变形曲线相适应的地表沉降最大值位置的计算方法，给出了一种与地表沉降最大值位置相协调的地表沉降影响范围x0的计算方法，在此基础上提出了一种改进的基于地层损失概念的地表沉降的预测方法。主要的结论：

1)先确定地表沉降最大值位置xm和地表沉降影响范围x0，再计算地表沉降最大值wmax这条计算路径可以避免出现多解问题。

2)地表沉降影响范围x0取值对地表沉降曲线的计算结果具有重要影响，本文所采用的基于主次影响分界求x0的方法是有效的，可以确保影响范围与最大值位置相互协调。

3)此改进方法整体预测效果较好，具有较强的工程实用性。