A Combined Shape and Topology Optimization Based on Isogeometric Boundary Element Method for 3D Acoustics

Jie Wang,Fuhang Jiang,Wenchang Zhao and Haibo Chen

CAS Key Laboratory of Mechanical Behavior and Design of Materials,Department of Modern Mechanics,University of Science and Technology of China,Hefei,230026,China

ABSTRACT A combined shape and topology optimization algorithm based on isogeometric boundary element method for 3D acoustics is developed in this study.The key treatment involves using adjoint variable method in shape sensitivity analysis with respect to non-uniform rational basis splines control points,and in topology sensitivity analysis with respect to the artificial densities of sound absorption material.OpenMP tool in Fortran code is adopted to improve the efficiency of analysis.To consider the features and efficiencies of the two types of optimization methods,this study adopts a combined iteration scheme for the optimization process to investigate the simultaneous change of geometry shape and distribution of material to achieve better noise control.Numerical examples,such as sound barrier,simple tank,and BeTSSi submarine,are performed to validate the advantage of combined optimization in noise reduction,and to demonstrate the potential of the proposed method for engineering problems.

KEYWORDS Combined shape and topology optimization;isogeometric boundary element method;shape sensitivity analysis;topology sensitivity analysis;adjoint variable method;sound absorption material

1 Introduction

Isogeometric analysis(IGA)[1]has been proposed to eliminate the gap between computeraided design(CAD)and computer-aided engineering(CAE),where non-uniform rational basis splines(NURBS)are widely used to represent geometry and approximate physical field variables,due to its advantages such as accurate description of geometry,high-order continuous fields,and flexible refinement.Compared with the finite element method(FEM)[2],boundary element method(BEM)[3]has exhibited superior performance in problems like exterior acoustics[4]because of its advantages including discretizing in boundary and fitting for infinite domain problems.The fully coupled FEM–BEM algorithm[5]was also proposed for acoustic-structural optimization design[6]to exploit the benefits of the two methods.Besides,various accelerated techniques such as adaptive cross approximation(ACA)[7],fast multipole method(FMM)[8–11],and wideband FMM[4,12,13],have also been adopted to improve BEM’s computational efficiency for large-scale problems.Considering that complex structures are usually described by NURBS patch in CAD software,which means that the geometry model are boundary-represented,the isogeometric boundary element method has also been successfully applied to potential problems[14–17],elastic problem[18–20],and acoustics[21–24].FEM–BEM coupled analysis method was also combined with IGA in elasticity[25].As the NURBS control points play a critical role in geometry construction,it is highly flexible to change the structural geometric shape.Refinement operators[1]such as h-refinement,p-refinement,and k-refinement have also been proposed to perfect IGA.Thus,conducting optimization design via IGA BEM is convenient.

The problem of sound emission of structures has attracted much attention in engineering practice.Structures such as sound barriers have also been investigated for their acoustic performance[26,27]in noise control.Baulac et al.[28]performed an optimization design of a sound barrier via BEM.Chen et al.[29]studied the distribution of absorbing material on a noise barrier by optimization design.Zhao et al.[30]applied topology optimization to the distribution of sound absorption material(SAM)that covers the structural surface with FMM BEM.Zhao et al.[31]also investigated the topology optimization of two different materials based on FEM–BEM coupled method.Liu et al.[32]and Chen et al.[33]conducted the sound barrier’s shape optimization by IGA BEM in 2D acoustics.Among these approaches,shape optimization and topology optimization are mainly used for designing structures to change their acoustic performance.

Shape optimization plays a great role in engineering problems to obtain the optimal shape under certain constraints with objectives.In this rational and automatic process,the geometry shape needs to be regenerated in each step,which causes limitation in conventional numerical analysis.In IGA,the structure surface is constructed by NURBS control points with weights and knot vectors;thus,the surface is easy to change by defining the control points as design parameters.Although IGA FEM has been firstly combined with shape optimization in fluid mechanics[34]and electromagnetism[35],IGA BEM is more suitable for the surface shape change in shape optimization,due to NURBS’and BEM’s features.Shape optimization has also been conducted through IGA BEM in heat conduction[36],wave resistance[37],elasticity[38–40],and acoustics[13,32,41].In engineering problems,sound structures may be covered with SAM or other materials.Different from design structure surface shape,the topology optimization focuses on finding the best topological distribution of SAM on the surface.Chen et al.[33]firstly conducted the topology optimization of the distribution of SAM on the sound barrier surface by IGA BEM with NURBS.Chen et al.[42]also studied the distribution of SAM via IGA BEM with subdivision surface method for 3D acoustics.Their findings demonstrated the frequency-dependent phenomenon in acoustic optimization design.

The previous works mainly conduct one type of optimization method to improve acoustic performance of structures.The present study focuses on combining the shape and topology optimization together efficiently to ensure better noise control for 3D acoustic problems.For combined optimization,researchers have done many works with the level set method(LSM)to conduct shape and topology update simultaneously by a uniform manner[43–45].Matsumoto et al.[44]adopted the LSM in the acoustic scatter problem to design the shape and topology of the structure.In this work,the topology optimization we considered is the distribution of SAM on structural surface.The solid isotropic material with penalization(SIMP)[46]method is applied to the initialization of design variables by converting the discrete density values of artificial material into continuous variables and enabling the intermediate density to approach 0 or 1,where 0 means that no material is on the design area.Thus,we select another type of combined optimization,where the shape and topology of structure should be changed by constructing a connection between them.Researchers have applied the deformable simplicial complex(DSC)method to combine shape and topology optimization in elasticity problems[47–49],where the topology design variables were updated first,and then the shape update was implemented subsequently.This process was called total iteration step of the combined optimization.Lin et al.[50]performed shape and topology optimizations through a time-dependent adjoint approach for sensitivity analysis in 2D acoustic metamaterials and phononic crystals,where shape optimization followed the topology optimization subsequently to modify the structural geometries.Jiang et al.[51]compared four iteration schemes by the second kind of combined optimization and successfully applied them to the noise reduction on sound barriers based on IGA BEM in 2D acoustics.In this paper,we mainly expand the best iteration scheme proposed by Jiang et al.[51]to 3D acoustics and applied it to complicated structures,where the NURBS control points coordinates are set as design parameters for shape design,and the artificial densities on NURBS integral elements are selected as the design variables for topology analysis.As both the two types of parameters are related to IGA BEM,a bridge is constructed between the structural shape and the distribution of SAM on the surface,which helps the shape and topology change in each iteration step.Meanwhile,using IGA BEM also avoids mesh regeneration,which improves the efficiency in the optimization process.

To implement combined optimization,the gradient-based optimizer is generally used due to its high efficiency,for example,the method of moving asymptotes(MMA)[52].This condition leads to the requirement of gradient information,which means additional step,i.e.,sensitivity analysis.The present study consists of two parts:shape sensitivity analysis with respect to the control points,and topology sensitivity analysis with respect to the artificial densities.Finite difference method(FDM),direct differentiation method(DDM)[4,12,53],and adjoint variable method(AVM)[30,54,55]are the three main methods for both the two types of sensitivity analysis.The DDM and AVM provide the analytical expression of sensitivity,and the AVM shows higher efficiency for multiple design variables.As the shape design parameters and topology design variables may be large in engineering,AVM is more suitable for ordinary optimization problems to achieve high efficiency.Here,we adopt the AVM for both the two types of sensitivity analysis.Another difficulty in IGA BEM for 3D acoustics is the non-uniqueness problem[56,57],especially for exterior acoustics.The Burton–Miller method[56,58]is adopted to overcome this problem,where Marburg[59]has investigated the influence of different coupling parameters on the analysis result.However,using this method also results in the problem of hyper singular integrals[41].Thus,the method based on subtraction of singularity technique[41,60]is also adopted to compute the singular integrals to achieve high accuracy.Moreover,to improve the efficiency of analysis conveniently,OpenMP tool in Fortran code is exploited in the matrix computation without changing the formulation of IGA BEM.

The present work is devoted to extending the combined optimization algorithm to 3D acoustics.The rest of this paper is organized as follows.In Section 2,the IGA BEM for 3D acoustics with the impedance boundary conditions are reviewed.Section 3 discusses the sensitivity analysis via AVM with respect to the NURBS control points and the artificial densities of SAM,respectively.Section 4 describes the three optimization procedure:shape optimization,topology optimization,and combined optimization.Section 5 introduces several numerical examples to validate the proposed approach.Finally,Section 6 provides the conclusions of this work.

2 Isogeometric BEM for 3D Acoustics

2.1 NURBS Surface for IGA

In IGA,we can define the knot vectorwhereis thei-th knot,nis the number of basis functions,andpgis the polynomial order.Then,B-spline basis functions can be defined as follows:

Forpg>1,we have the following basis functions:

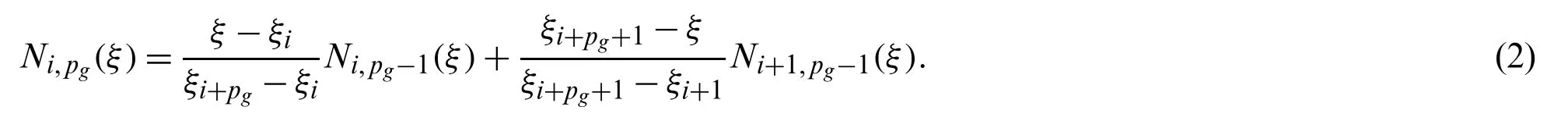
Then,a B-spline curve’s formulation can be described by

where x(ξ)is the point located on the curve,and Piis thei-th control point that corresponds to the knot.

For B-spline surface,we need two knot vectorsΞ1= {ξ1,ξ2,...,ξn+pg1+1} andΞ2={η1,η2,...,ηm+pg2+1},wherenandmare the numbers of basis functions for each parametric dimension.The formulation of B-spline surfaces can be described as follows:

By introducing a weightwi,jwith each control point,NURBS basis functions for two dimensions can be obtained as

Similarly,the NURBS surface formulation can be described as follows:

where the number of control points is represented byNg=n×m.The derivative of the NURBS basis function was discussed by Simpson et al.[18].

2.2 Isogeometric BEM for Acoustics

Considering a domainΩwith a boundaryΓ,the Helmholtz equation that governs the acoustic field can be described as

wherepdenotes the sound pressure,k=ω/cdenotes the wave number,ωis the angular frequency,andcis the wave velocity in the acoustic medium.Here,we selecte−iωtas the harmonic time dependence,wheretdenotes time.

For boundary element method,by applying Green’s second theorem and letting point x approach the boundary,we can obtain the conventional boundary integral equation(BIE),referred to as CBIE,and its outward normal BIE,referred to as HBIE.The formulations can be described as follows:

where s and x are the source point and field point,respectively;∂p(x)/∂n(x)=q(x)denotes the flux of sound pressure;pin(s)indicates the sound pressure of the incident wave at point s;n(x)denotes the outward normal vector at point x,and jump termc(s)is equal to 1/2 if the boundaryΓis smooth around the source point s.

The Green’s function for 3D acoustics is given as follows[41]:

wherer=|s −x|denotes the Euclidean distance between points s and x.

In this study,we consider the impedance boundary condition

whereβ(x)denotes the normalized surface admittance at field point x.

In IGA BEM,the NURBS interpolations are applied to both the geometry and physical fields.In this study,we adopt different NURBS interpolation formulations to suit physical analysis,which means that the physical field is separated from the geometry.The knot vectors of the physical space can be represented asΞd1andΞd2.Thus,the physical field variables can be expressed as follows:

whereplandqldenote the sound pressure and flux coefficients associated with thel-th physical control point,respectively;Ndis the total number of physical control points;andβxrepresents the acoustic admittance at point x(ξ,η).

The location of collocation points in parametric space can be obtained by the Greville abscissa as follows:

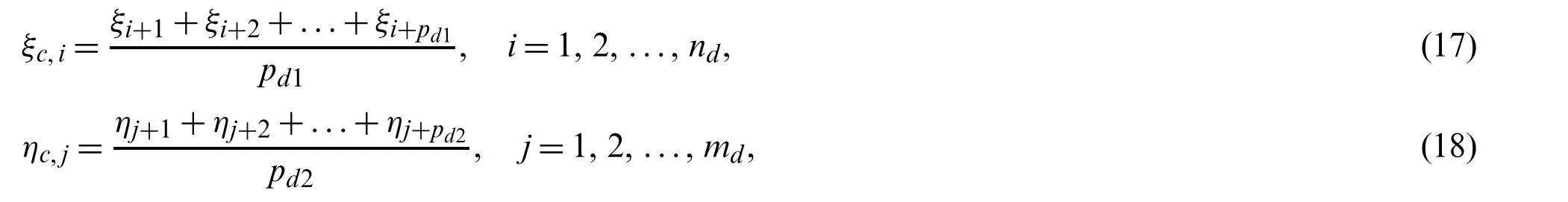
wherepd1andpd2denote the orders of basis function of each dimension,respectively;ndandmdare the number of collocation parameters in each dimension,andmd×nd=Nd.

Similarly,after discretizing the boundary intoNe1×Ne2=Neintegral elements,Eqs.(8)and(9)can be rewritten as

where[ξa,ξa+1]×[ηb,ηb+1]denotes the parameter space of an integral element;J(ξ,η)represents the Jacobian;(ξc,i,ηc,j)and(ξ,η)denote the two parameters of the source point s and field point x,respectively;βsdenotes the acoustic admittance at the source point s(ξc,i,ηc,j),and we assume that the admittance keeps the same value over each element.The local support of NURBS basis functions,where a maximum of(pd1+1)×(pd2+1)basis functions are nonzero for values,can reduce the computation effort for the integral coefficient.

When the parameter(ξc,i,ηc,j)of the source point lies within the element parametric space[ξa,ξa+1]×[ηb,ηb+1],weak and hyper singularities appear in the kernel functions of Eqs.(19)and(20),respectively.Here,the detailed treatment of singular integrals is referenced in the use of Guiggiani method[60]by Chen et al.[41].

By adopting the Burton–Miller formulation[58]with coefficient[59],Eqs.(19)and(20)can be combined and formulated as the matrix equation

where p is the complex vector of the physical values at the physical control points;and pinand qindenote the incident wave vectors of sound pressure and flux,respectively.

After Eq.(21)is solved,the sound pressure of points lying in the domain can be obtained by

where the computations of matrices Gf,Hf,and vector pinfare similar to those in Eq.(21).

3 Sensitivity Analysis through IGA BEM

Sensitivity analysis can obtain the derivatives of objection function with respect to different kinds of design variables.Thus,this type of analysis plays a critical role in the optimization process.The shape sensitivity and topology sensitivity analyses are presented in this section.

3.1 Shape Sensitivity Analysis

Control points usually control the configuration of structure surface in IGA,which means that they can be naturally set as the design parameters in shape optimization.In this study,we set certain control points of the NURBS surface as design parameters to change the shape,and the AVM proposed by Zheng et al.[54]is adopted for shape sensitivity analysis.

In DDM,Eqs.(8)and(9)can be differentiated with respect to the design parameterγe(usually represents thex,y,orzcoordinate of a certain control point)as

where the sensitivities of the kernel function are presented as

The sensitivity interpolation by NURBS basis functions are presented as

Similarly,using the same discretization as in Eq.(19),we can express Eqs.(23)and(24)as

Subsequently,still based on the Burton–Miller formulation,Eqs.(32)and(33)can be combined and expressed by matrix form as

where matrices H and G have been computed by Eq.(21).anddenote the vector ofandrespectively.andare the derivatives of G and H.The detailed formulation of singular integrals in Eqs.(32)and(33)is presented in the work of Chen et al.[41].

For sensitivity analysis via DDM,after Eq.(34)is solved,the source point s is placed at the acoustic domainΩ,and their sensitivities can be calculated by

However,some engineering problems may require more design parameters to guarantee the complexity of the structure,and the objective function in the optimization process may be merely related to physical values at field points.Thus,the AVM is adopted for ordinary optimization design.In accordance with Eqs.(34)and(35),the formulation can be rewritten as

where the calculation of(H −G)−1usually requires extensive effort.To avoid this process,we introduce the following adjoint equation:

and thus,the value of adjoint matrix U can be obtained by

Finally,by substituting Eq.(38)into Eq.(36),we can calculate the new formulation for the shape sensitivities at field points as follows:

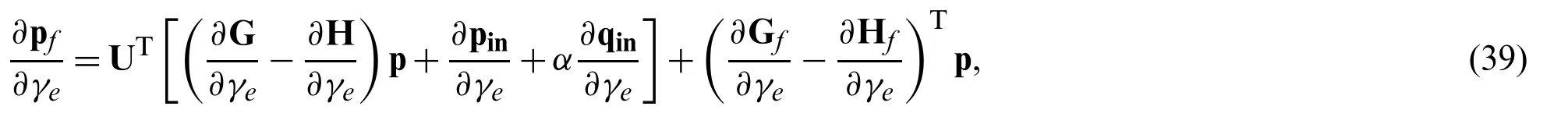
Evidently,the adjoint matrix U is independent of all the design parameters,which means that Eq.(37)needs be solved once even if a large number of design parameters exist.Thus,the AVM can significantly improve the efficiency of shape sensitivity analysis.

3.2 Topology Sensitivity Analysis

In this study,we investigated the topology optimization of the distribution of SAM on structural surface,which is a problem with discrete values of 0 or 1,so that the mathematical computation in sensitivity analysis can be conducted.The SIMP method[46]is adopted to transform the discrete values into continuous values.The artificial densityρeof thee-th element is set as the design variable to conduct the topology optimization process.The formulation of admittance can be expressed as

whereμdenotes the penalization factor,and we defineμ=3 in the analysis.β0represents the normalized surface acoustic admittance.Here,we set its value as 0.1 for simplicity.

As the artificial density of the material of each element is set as a design variable,the AVM is also implemented for higher efficiency in topology sensitivity analysis.Usually,the objective function is related to the sound pressure of the field points asΠ(pf),and in accordance with Eqs.(21)and(22),it can be rewritten as

The derivatives of objective functionΠ(pf)can also be expressed as

where the termu3does not contain any term aboutand.

Combining Eq.(42)with Eq.(43)yields

As bothλ1andλ2are arbitrary,they can satisfy the following adjoint equations

and by solving Eq.(45),the derivative of objective function can be obtained by

Evidently,both the adjoint operatorsλ1andλ2should be computed only once for all the design variables.This feature significantly improves the efficiency of topology sensitivity analysis,which plays a significant role in the subsequent topology optimization process.The values of,andu3are determined by objective function.The objective functionΠin optimization design is usually defined as the sound pressure related to the local evaluation or sound power[61–63]related to the global estimation.This topic is discussed in Section 4.

4 Combined Shape and Topology Optimization

In this work,we present the combined shape and topology optimization to change the geometric shape and distribution of SAM on structural surface simultaneously.IGA BEM is applied to gradient-based optimization algorithm to construct a bridge between these two types of optimization process.After obtaining the two types of sensitivities in Section 3,we select the method of moving asymptotes(MMA)developed by Svanberg[52]as the optimization solver to update the design variables in each iteration step.

4.1 Shape Optimization

The optimization model of shape optimization can be described as follows:

where the objective functionΠis set as the average sound pressure level(SPL)ofnfobserved points.pHfis the conjugate transpose of pf.The design parameterγevaries between the lower boundand the upper boundandnsis the number of design parameters.

V(γe)denotes the volume of the structure that should not be larger than the initial structure volumeV0,where we called the maximum volume constraint.The formulations of volume constraint and its sensitivity are expressed as

where x and n denote the point on NURBS surface and its external unit normal vector,respectively.

In each iteration step,the design parameters are updated until the objective functionΠis converged,whereτis the given value that determines whether the iteration has to be stopped.

4.2 Topology Optimization

As mentioned in Section 3.2,we change the distribution of SAM to minimize the average SPL of observed points.The optimization model is expressed as

In the topology optimization,we select the same objective function and its sensitivity as those in shape optimization,where the values ofandu3in Eq.(43)can be obtained as

4.3 Combined Optimization

According to Chen et al.[33],both shape optimization and topology optimization exhibit good acoustic performance.For single shape optimization or topology optimization,the main process shown in Figs.1a and 1b mainly includes the input of the NURBS model,initialization of the optimization model,acoustic analysis based on IGA BEM,shape or topology sensitivity analysis,and optimization solver through MMA to update the design parameters/variables.

In this study,the target is to combine the geometry shape change and distribution of SAM simultaneously to achieve better acoustic performance than the single type of optimization.Thus,the key is to select a suitable iteration scheme to combine these two types of optimization process.Considering the computational efficiency and their features in the optimization process,the presented scheme is shown in Fig.1c,where each outer iteration step includes an inner iteration process that consists of a converged topology optimization and a one-step shape optimization.Although we have used the SIMP method,some elements may still exhibit intermediate densities between 0 and 1,which are the so-called gray elements.Here,the density operator based on a smoothed Heaviside function is adopted to eliminate these elements,and the detailed formulation was discussed by Zhao et al.[30].

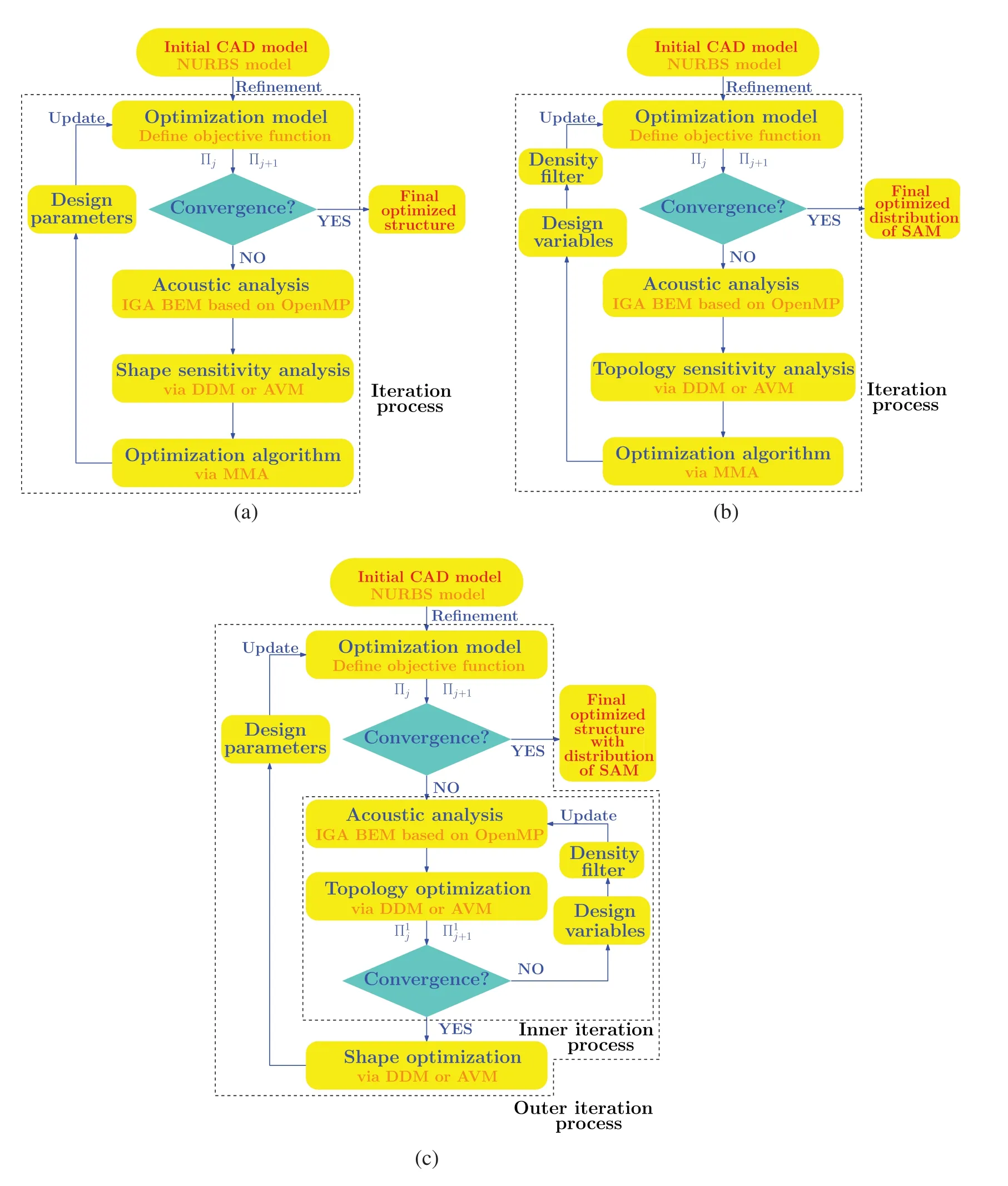
Figure 1:Flow chart of three optimization processes based on IGA BEM(a)Shape optimization process(b)Topology optimization process(c)Combined optimization process

5 Numerical Examples

Several numerical examples are presented to validate the applicability of the proposed approach and show its potential in engineering problems.Here,all the examples are exterior acoustic problems,and the parameterτfor the optimization process is set to 10−4.The code is parallelized by using the OpenMP tool in Fortran to improve the computational efficiency.

5.1 Scattering Sphere

A scattering sphere model is considered to verify the shape sensitivity analysis and topology sensitivity analysis of the present approach.The sphere center is located at point(0,0,0)with a radiusr0=1.0 m as shown in Fig.2a,where an incident plane wave with a unit amplitude is traveling along thez-axis as an excitation.The wave velocity isc=340 m/s.Figs.2b and 2c show the 26 NURBS control points and their weights for the spherical surface,where the coordinates are(1,0,0)for P14,(0,1 ,0)for P22,and(0,0,1)for P11.Here,we consider that all the discretized elements are covered with SAM,which means an initial artificial density ofρe=1.0.The observed point is set as(0,2,0).

Figure 2:Scattering sphere(a)Physical model(b)NURBS model with control points(c)Weights for control points

Fig.3 shows the computation time of IGA BEM on acoustic analysis accelerated by OpenMP tool,where the more threads used in computation,the less time is needed.As the figure shows,the efficiency of OpenMP tool using 56 threads can be 20 times faster than the ordinary code.Moreover,compared with the FMM[32],adopting OpenMP tool only needs to change a few for the code,which becomes more convenient for the analysis.

Figure 3:Computing times of IGA BEM accelerated via OpenMP tool on acoustic analysis

For the computation of sound sensitivities with respect to shape parameters,they-coordinate of the control point P22is selected as the design parameter,which varies from 0.5 m to 1.5 m.The computation frequency is 100 Hz.To validate the AVM,we compare it with the DDM and FDM,where the step size of the design parameter in FDM is set as 0.0001 to ensure sufficient accuracy.As Fig.4 shows,all results of the three methods are in good agreement in the real and imaginary parts of the sensitivities,which validates the correctness of the DDM and AVM.Furthermore,the time to obtain the observed point’s shape sensitivity through the DDM and AVM is illustrated in Fig.5.Obviously,with the increase of the number of design parameters,the AVM takes less time than the DDM,which demonstrates its advantage in accelerating shape sensitivity analysis with multiple design parameters.

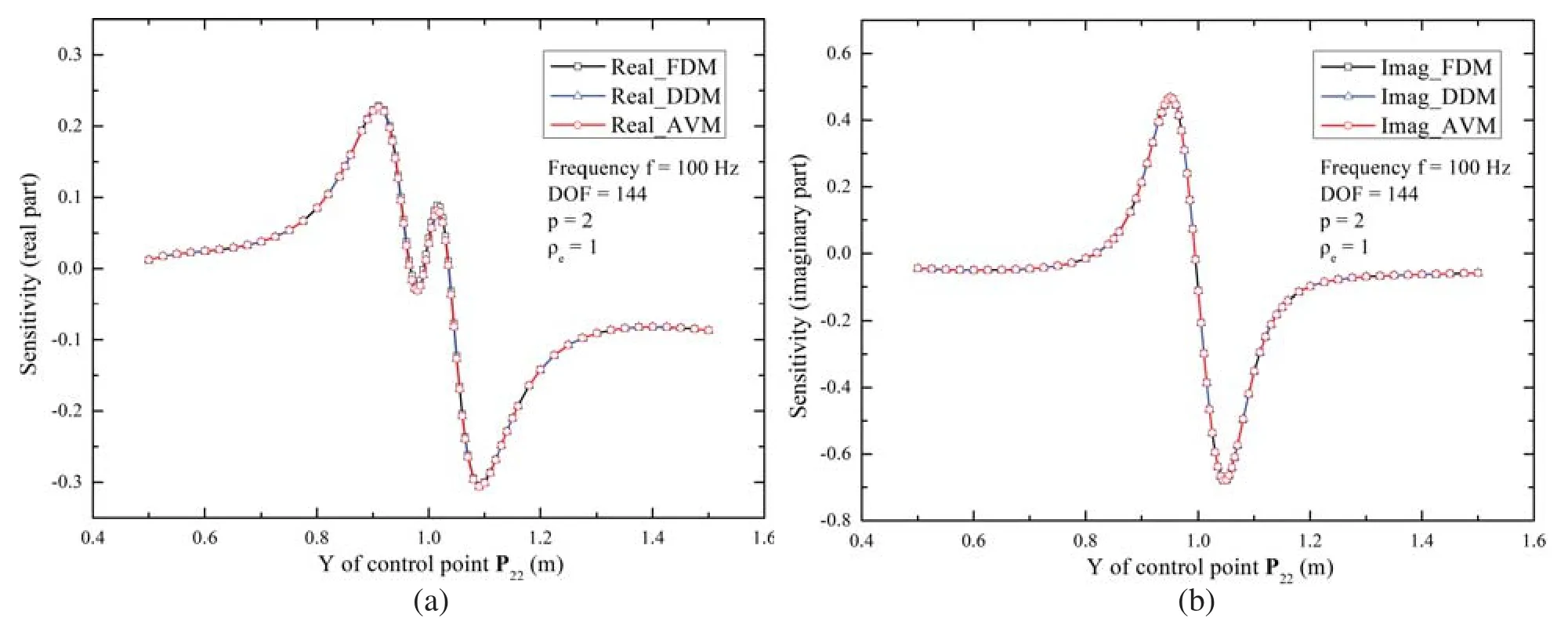
Figure 4:Sound pressure sensitivities at point(0,2,0)with respect to y-coordinate of control point P22(a)Real part(b)Imaginary part

Figure 5:Computing times of DDM and AVM in obtaining sensitivities of the observed point

The verification of topology sensitivity analysis is also shown in Fig.6,where we set the objective function as the SPL at the observed point.The result of AVM is also compared with those of DDM and FDM.As the figure shows,the three methods provide the same results in sensitivities of the objective function,which validates the correctness of the analytical algorithms,i.e.,DDM and AVM.Fig.7 reveals the efficiency of the DDM and AVM in topology sensitivity analysis.When the number of design variables is less than 256,the DDM takes less time than the AVM,while the AVM shows higher efficiency when the number of design variables is larger than 256.Furthermore,the results of efficiency in Figs.5 and 7 also demonstrate that topology sensitivity analysis usually takes less time than shape sensitivity analysis,even if we set more design variables for topology analysis.The reason is that the computation of shape sensitivity in matrices H and G with respect toγetakes much time when the geometry shape changes,whereas the geometry remains the same in topology optimization.Thus,topology optimization presents higher computation efficiency than shape optimization.

Figure 6:Sensitivities of SPL at point(0,2,0)with respect to artificial density ρe

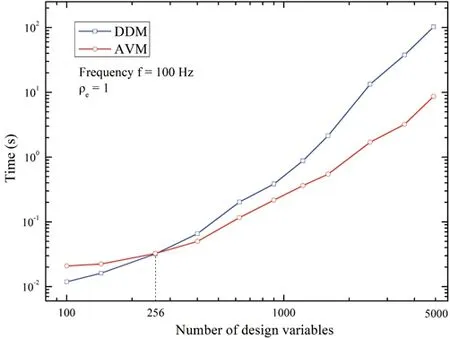
Figure 7:Computing times of topology sensitivity evaluation via DDM and AVM

5.2 Sound Barrier

Although sound barriers have been simplified as 2D problems for optimization design by using the IGA BEM in the work of Liu et al.[32]and Chen et al.[33],we conduct a more practical 3D model forΓ-shaped sound barrier in this study.Generally,the sound barrier is considered as a half-space acoustic problem in engineering practice,and thus,the kernel function and its sensitivities in Eqs.(10)and(25)need to be substituted by the following formulations:

As shown in Fig.8,a mono-pole source is located at point(0,1,1),and the initial state of the barrier is that all the surfaces are covered with SAM.The NURBS model is discretized by 1156 integral elements.After the IGA discretization,the maximum element size is about 0.25 m.The initial filter radius in topology optimization is set as 0.1 m.The design parameters for shape optimization are the x-coordinates of the control points from points 1 to 12 on the left surface as depicted in Fig.8c.The initial values of shape design parameters are exhibited in Tab.1,and their lower and upper bounds are ±0.1 m based on the initial values.For the observed points,we select 27 points that are evenly distributed in the reference domain within the coordinates x ∈[7,9],y ∈[−1.4,1.4]and z ∈[0.2,2.6].

Figure 8:Initial sound barrier model(a)Physical model(b)NURBS model(c)Size of sound barrier(d)Cross section

Table 1:Design parameters in sound barrier model for shape optimization

Fig.9 shows the iteration histories of the objective function by using the three optimization methods.Compared with the other two methods,the shape optimization is only reduced slightly for the average SPL at the lower frequency of 200 Hz.These results are contrary to those reported by Liu et al.[32],where the sound barrier has been set as a rigid boundary condition and defined as a 2D model.Thus,this finding also demonstrates that all the surfaces covered with SAM may not be a good choice for the initial model state before shape optimization.For the shape optimization,the purpose is usually to let the scatter waves and incident waves interfere with each other more by shape change.However,most sound waves have been absorbed if all the surfaces are covered with SAM.Nevertheless,the combined optimization in this example still obtains a better noise reduction than a single type of optimization.Furthermore,as shown in Fig.9,the proposed method for combined optimization can achieve better results at higher frequency of 500 Hz.Fig.10 shows the iteration histories of the volume constraint for the two types of optimization.As we can see,all the results satisfy the volume constraints in the optimization models,which means that the optimization models are fit for this problem.

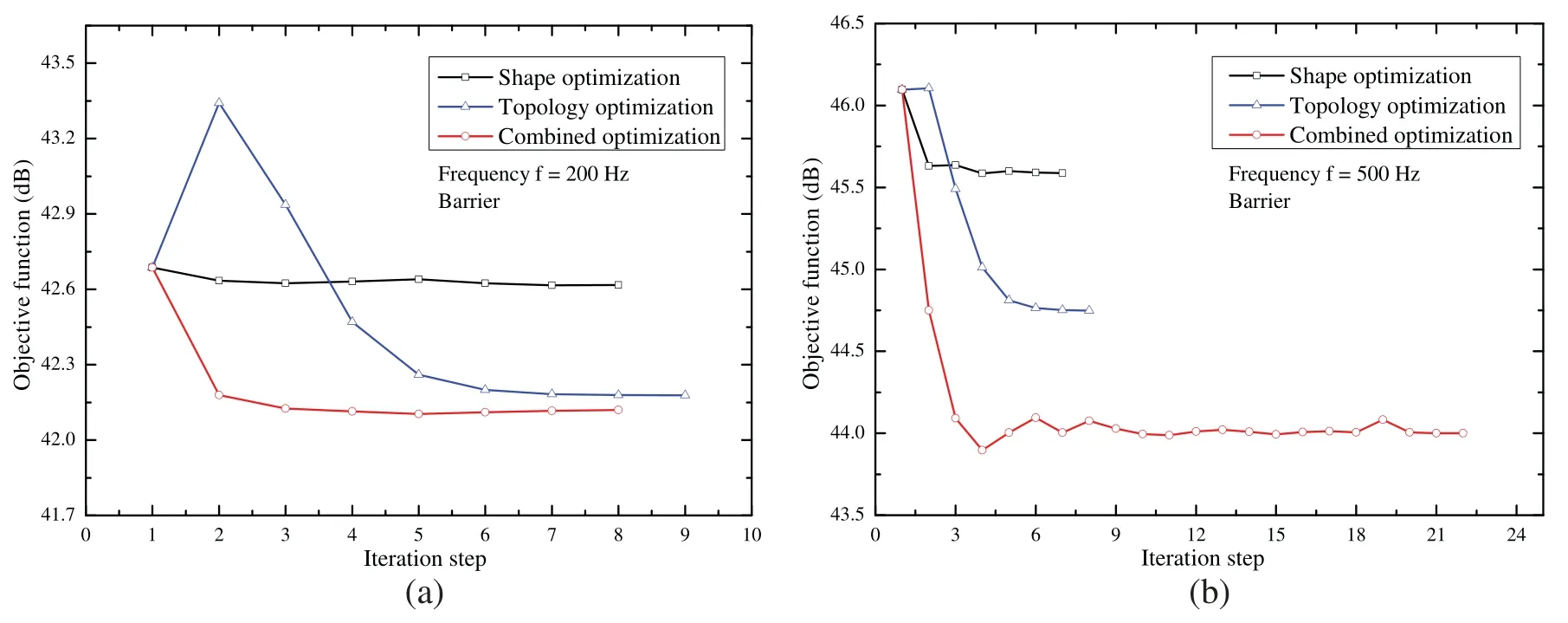
Figure 9:Iteration histories of sound barrier’s objective function by using three optimization methods(a)Frequency f =200 Hz(b)Frequency f =500 Hz

Figure 10:Iteration histories of sound barrier’s volume constraint for shape optimization and topology optimization(a)Shape optimization(b)Topology optimization

Figs.11 and 12 show the optimization results of the sound barrier by using the three optimization methods.As Tab.1 shows,the final optimized shape changes slightly compared with the initial structure in the shape optimization process,which means that the range of shape design parameters may not be large,while a larger range of lower and upper bounds usually offers more values for design parameters to be chosen in each optimization iteration step.For the results of topology optimization,the distribution layout of SAM tends to occupy many smaller areas at a higher frequency of 500 Hz.The reason is that the higher the frequency,the shorter the wavelength,the more sensitive the shape of the structure surface and the distribution of the material to the wavelength.For the combined optimization,the results’trend is consistent with the single type of optimization in shape or topology,but some details have changed.Overall,the results of the three optimizations are frequency dependent,which shows different surface shapes and distributions of SAM with the increase in computation frequency.

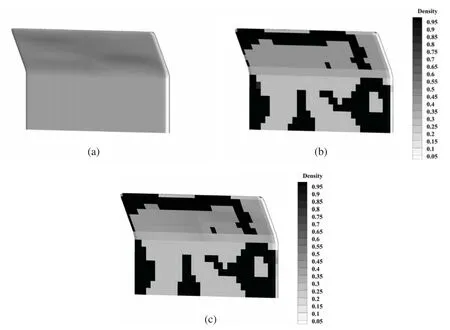
Figure 11:Optimization results of sound barrier by using three optimization methods at frequency f =200 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

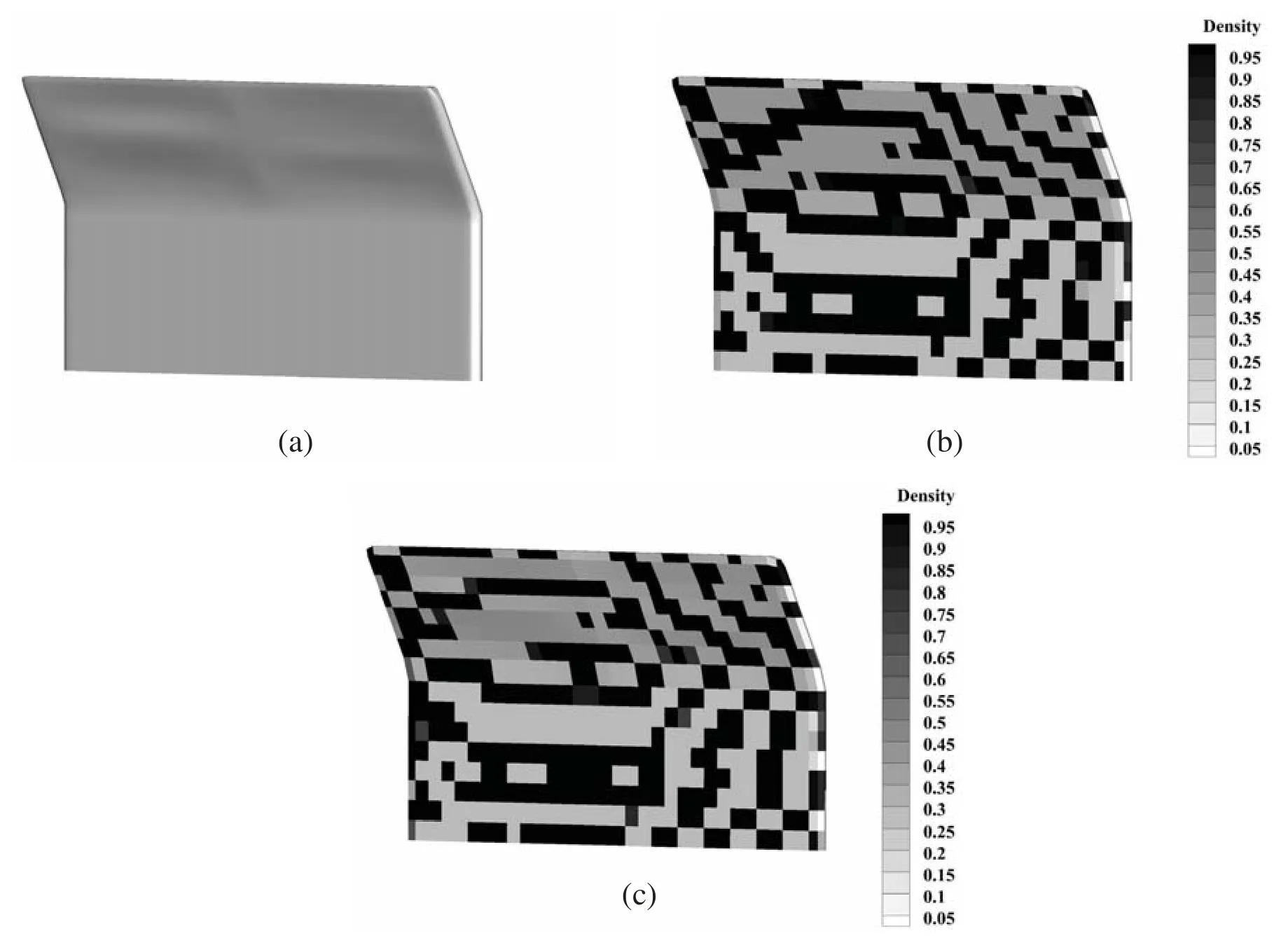
Figure 12:Optimization results of sound barrier by using three optimization methods at frequency f =500 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

For the topology optimization at a higher frequency off=500 Hz,as shown in Fig.12b,the result encounters checker-board problem.This phenomenon is mainly caused by the setting of small filter radius forrmin=0.1 m in the sensitivity filter operator.By increasing the value ofrmin,as Fig.13 shows,checker-board phenomenon will be weakened.However,for the noise reduction by topology optimization,as Fig.14 shows,the larger the value ofrminis,the less decreases the objective function after optimization.Besides,the topology optimization model in this study is based on the distribution of SAM on the structure surface,so the checker-board problem actually have little influence on the physical meaning and application to engineering practice,where every element of the structure surface can be covered with a piece of SAM flexibly.Overall,to achieve better noise reduction,we still select 0.1 m as the filter radius.

Figure 13:Optimization results of sound barrier with filter radius rmin = 0.6 m at frequency f =500 Hz

Figure 14:The impact of filter radius on objective function for sound barrier’s topology optimization at frequency f =500 Hz

5.3 Simple Tank

The example of a underwater simple tank presented by Chen et al.[41]is analyzed in this section.Fig.15 shows the model in physics and geometry.Herein,the wave velocity is 1500 m/s.An incident wave with a unit amplitude travels along the negativey-axis to the model.The model is discretized by 1600 integral elements for IGA BEM.The maximum element size along the direction that is parallel toz-axis is about 1.1 m,and the maximum size of circumferential element is about 2 m.The initial filter radius is set as 0.1 m.The parameters for shape design are the y-coordinates of control points from points 1 to 6 on the right surface,as shown in Fig.15b.The initial values and side constraints of design parameters for shape optimization are exhibited in Tab.2.We select the observed point as point(10,10,0).Furthermore,different from the usual rigid boundary condition,all the surfaces of the structure are covered with SAM in this simulation.

Figure 15:Initial simple tank model(a)Physical model(b)NURBS model with control points(c)Weights for control points

Table 2:Design parameters in simple tank model for shape optimization

Fig.16 shows the iteration histories of objective function for the three optimization methods on the simple tank.We have expanded the range of parameters for shape design,as depicted in Tab.2;thus,this time the shape optimization achieves a good noise reduction,even better than the topology optimization at 200 Hz.Again,the combined optimization achieves the best results compared with the other two single optimization methods,with the trend of more reduction for the objective function at higher frequency.The iteration histories of volume constraints are shown in Fig.17.The volumes of optimized structures are less than those of the initial structures,and the final volume fractions of SAM are also less than 0.5.

Figure 16:Iteration histories of objective function of simple tank using three optimization methods(a)Frequency f =200 Hz(b)Frequency f =500 Hz

Figure 17:Iteration histories of simple tank’s volume constraint for shape optimization and topology optimization(a)Shape optimization(b)Topology optimization

Figs.18 and 19 show the optimization results of simple tank by using the three optimization methods.Compared with the initial structure,the optimized shapes have changed obviously after shape optimization and combined optimization.This is mainly due to the expanded side range of the shape design parameters.For topology optimization,the SAM tends to be more spread at higher frequency.However,few gray elements still appear after the optimization,although we have conducted a density filter operator.Finally,the combined optimization also shows a detailed change in shape or distribution of material compared with the single type of optimization.These figures also demonstrate that the phenomenon of frequency dependence for optimized shape and distribution of material is clear.

Figure 18:Optimization results of simple tank by using three optimization methods at frequency f =200 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

Figure 19:Optimization results of simple tank by using three optimization methods at frequency f =500 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

An obvious checker-board phenomenon is also indicated by Fig.19b,and thus,we also test the mesh-dependency problem.As exhibited in Fig.20,the checker-board phenomenon still appears if we only keep the filter radiusrminas a small value 0.1 m.By increasing the value ofrmin,this phenomenon will also be weakened,as shown in Fig.21.Finally,to achieve better noise reduction,we still adopt the initial filter radiusrmin=0.1 m.

Figure 20:Topology optimization result of simple tank with 6400 NURBS elements and filter radius rmin=0.1 m at frequency f =500 Hz

Figure 21:Topology optimization result of simple tank with filter radius rmin=1.6 m at frequency f =500 Hz

5.4 BeTSSi Submarine

To exhibit the capability of the proposed algorithm in optimization design of complicated geometry,the BeTSSi submarine model described by Venås et al.[22]is considered in this section.Now we adopt a half size scale of this model for analysis.Moreover,we have reconstructed the submarine by NURBS,where the submarine consists of 7 NURBS patches;thus,the optimization based on IGA BEM for 3D acoustics is extended to the problem of multi-patch structures[64].The discontinuous element method[64,65]is also applied to IGA BEM for 3D acoustics.Figs.22a and 22b show the submarine’s NURBS model,control points,and weights.Shape design parameters are set as thez-coordinates of 8 control points depicted in Fig.22c.The model is immersed in water.A plane wave with a unit amplitude propagates along the negativez-axis direction.The target of optimization is to minimize the SPL at an observed point(3,0.3,4).The initial values and side constraints of shape design parameters are listed in Tab.3.The number of NURBS integral elements for computation is 2172.

Figure 22:BeTSSi submarine via NURBS(a)NURBS model and control points(b)Weights for control points(c)Shape design parameters

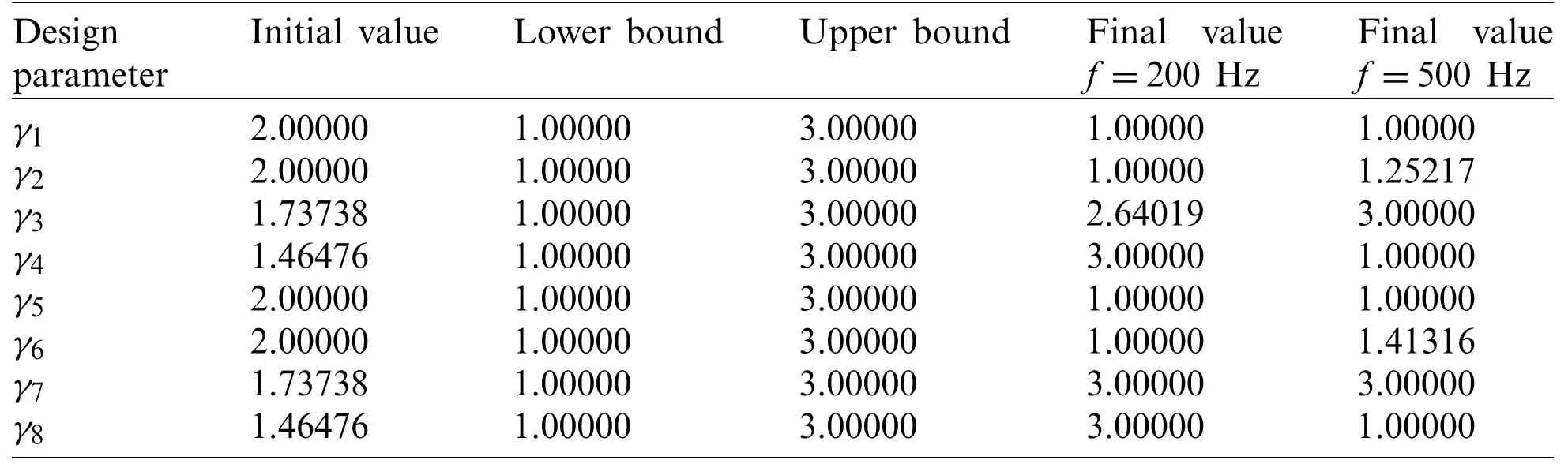
Table 3:Design parameters in BeTSSi submarine for shape optimization

The iteration histories of objective function through the three optimization methods at different frequencies are shown in Fig.23.Similar to the results of the simple tank model in Section 5.3,the combined optimization method achieves the best SPL reduction at the observed point,and the value of the objective function decreases rapidly in the initial optimization steps.It finally reduces even for 20 dB at a higher frequency of 500 Hz.For the volume constraint,as Fig.24 shows,the volumes of geometry shape and SAM also satisfy the constraints in the two types of optimization models.

Figure 23:Iteration histories of objective function of BeTSSi submarine using three optimization methods(a)Frequency f =200 Hz(b)Frequency f =500 Hz

Figure 24:Iteration histories of BeTSSi submarine’s volume constraint for shape optimization and topology optimization(a)Shape optimization(b)Topology optimization

Figs.25–28 show the optimization results for the submarine through the three optimization methods at frequencyf=200 Hz andf=500 Hz.For shape optimization,the optimized shape appears two peaks near the end of the design domain,which may result in a slight increase of the surface area on the design domain.The two peaks tend to be smaller at a higher frequency of 500 Hz.For topology optimization,a few intermediate density elements still exist in the final results.The total distribution trend of SAM after optimization is similar to the propagation of a water wave,and is also more spread at a higher frequency of 500 Hz.The final shape and distribution of material for the combined optimization still shows detailed differences compared with the single type of optimization.All the results have shown the valid application of the proposed method on complex structures.

Figure 25:Surface SPL of optimized structure via three optimization methods at frequency f =200 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

Figure 26:Distribution of SAM after optimization at frequency f =200 Hz(a)Topology optimization(b)Combined optimization

Figure 27:Surface SPL of optimized structure via three optimization methods at frequency f =500 Hz(a)Shape optimization(b)Topology optimization(c)Combined optimization

Figure 28:Distribution of SAM after optimization at frequency f =500 Hz(a)Topology optimization(b)Combined optimization

6 Conclusion

In this study,we developed a combined shape and topology optimization algorithm for 3D structures based on IGA BEM.Different from the past shape optimization method on rigid structures,the impedance boundary condition is applied to the optimization process,where the structure surfaces are covered with SAM with artificial densities.The NURBS model constructs a bridge between geometry and physics,when surface shapes and the distribution of material change in each optimization iteration step.The control points are selected as the design parameters for shape optimization on account of their convenience and flexibility in shape control.With the application of SIMP method,the artificial densities of SAM located in integral elements are set as the design variables for topology optimization.The AVM is applied to the sensitivity analysis with respect to shape design parameters and topology design variables.Considering the computational efficiency and features of the two types of optimization,an iteration scheme for combined optimization,including a convergent topology optimization and a one-step shape optimization,is investigated in this study.Several numerical examples,including a complex submarine scattering model,are performed to demonstrate the potential of the proposed combined optimization in achieving improved noise reduction,compared with the single type of shape optimization or topology optimization.All the optimization processes obtain frequency-dependent results,where the optimized shape and distribution of material at higher frequency tend to show a better noise reduction.

In the future,we aim to apply the fast multipole method to the acoustic analysis and sensitivity analysis to expand the developed method to larger-scale engineering problems.The level set method is also considered replacing the SIMP method in topology optimization to eliminate the medium densities in the distribution of SAM.

Funding Statement:This study was financially supported by the National Natural Science Foundation of China(NSFC)under Grant No.11772322,and the Strategic Priority Research Program of the Chinese Academy of Sciences under Grant No.XDB22040502.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.

Appendix A

The reconstructed BeTSSi submarine model consists of 7 NURBS patches,which are shown in Fig.29.

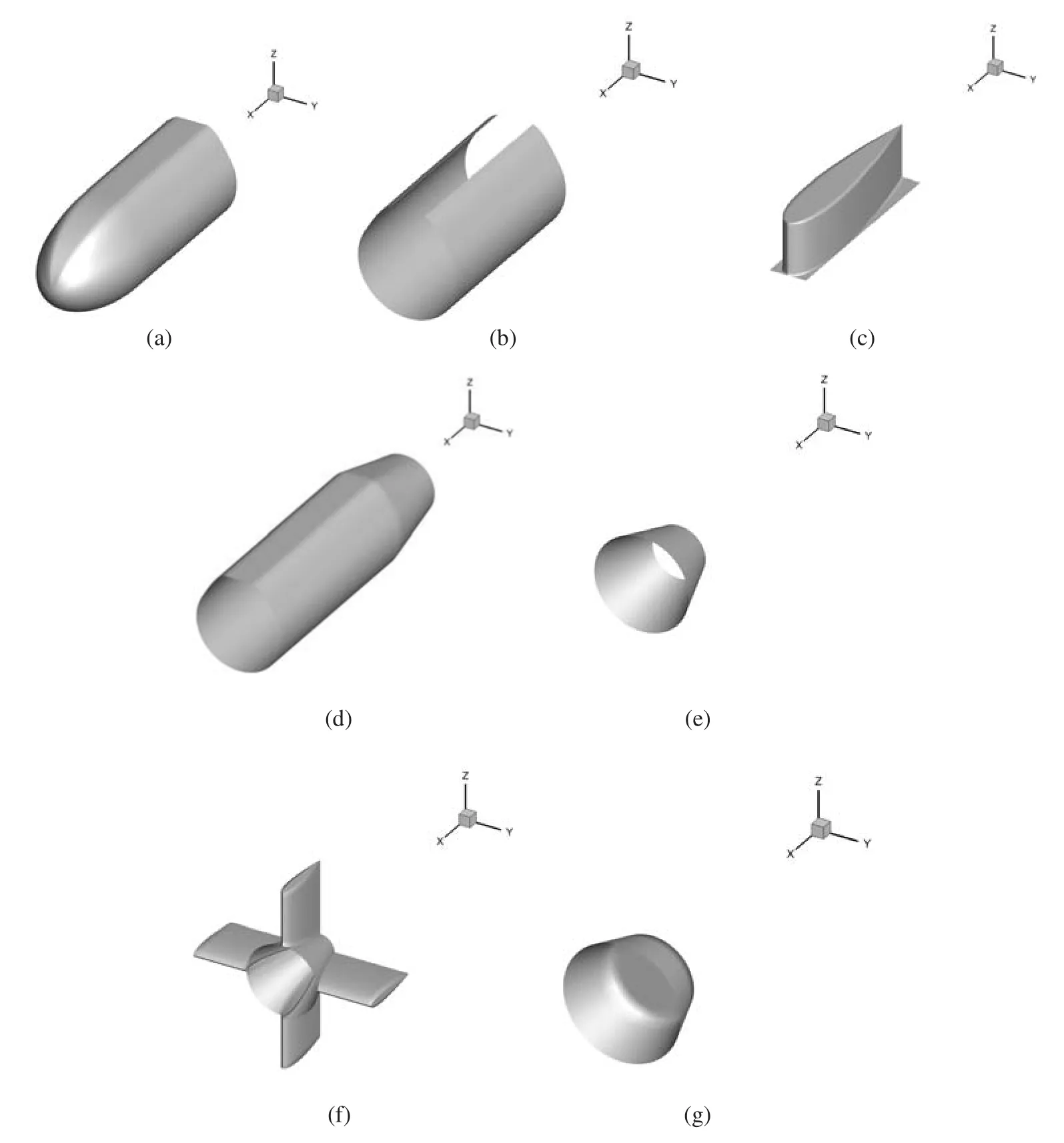
Figure 29:7 NURBS patches of submarine model.(a)Patch 1.(b)Patch 2.(c)Patch 3.(d)Patch 4.(e)Patch 5.(f)Patch 6.(g)Patch 7