A New Modified Inverse Lomax Distribution:Properties,Estimation and Applications to Engineering and Medical Data
2021-07-30AbdullahAlmarashi
Abdullah M.Almarashi
Department of Statistics,Faculty of Science,King Abdulaziz University,Jeddah,21589,Saudi Arabia
ABSTRACT In this paper,a modified form of the traditional inverse Lomax distribution is proposed and its characteristics are studied.The new distribution which called modified logarithmic transformed inverse Lomax distribution is generated by adding a new shape parameter based on logarithmic transformed method.It contains two shape and one scale parameters and has different shapes of probability density and hazard rate functions.The new shape parameter increases the flexibility of the statistical properties of the traditional inverse Lomax distribution including mean,variance,skewness and kurtosis.The moments,entropies,order statistics and other properties are discussed.Six methods of estimation are considered to estimate the distribution parameters.To compare the performance of the different estimators,a simulation study is performed.To show the flexibility and applicability of the proposed distribution two real data sets to engineering and medical fields are analyzed.The simulation results and real data analysis showed that the Anderson-Darling estimates have the smallest mean square errors among all other estimates.Also,the analysis of the real data sets showed that the traditional inverse Lomax distribution and some of its generalizations have shortcomings in modeling engineering and medical data.Our proposed distribution overcomes this shortage and provides a good fit which makes it a suitable choice to model such data sets.
KEYWORDS Inverse lomax distribution;logarithmic transformed method;order statistics;maximum likelihood estimation;maximum product of spacing;manuscript;preparation;typeset;format
1 Introduction
Inverse Lomax(IL)distribution is a very important lifetime distribution which can be used as a good alternative to the well known distributions such as gamma,inverse Weibull,Weibull and Lomax distributions.It can be considered as a member of generalized beta family of distributions.It has different applications in modelling various types of data including economics and actuarial sciences data because its hazard rate can be decreasing and upside down bathtub shaped.The random variableXis said to have an IL distribution if its probability density function(PDF)is

The cumulative distribution function(CDF)of(1)is

whereαis the shape parameter andθis the scale parameter.For more details about the inverse distributions one can refers to[1–4].The traditional IL distribution does not give a good fit for modeling many real life data such as in reliability and biological studies.Recently,many generalizations of IL distribution have been developed.Hassan et al.[5]introduced Weibull IL distribution and studied some of its statistical properties.Maxwell et al.[6]proposed the Marshall-Olkin IL distribution by adding a new shape parameter for more flexibility.ZeinEldin et al.[7]used the alpha power method to add a new shape parameter to the IL distribution and proposed a new distribution which called alpha power IL(APIL)distribution.In spite of these generalizations,still a new generalization of IL is needed because these distributions are not able to model various types of data.
The main objective of this paper is to propose a new form of the IL distribution by adding a new shape parameter to the CDF in(2)using the same approach of[8].They introduced a new method to add an extra shape parameter to an existing distributions which called the logarithmic transformed(LT)method.The LT method has the following CDF and PDF

and

respectively,withλ>0,λ/=1.By takingin(3)of the IL distribution CDF in(2)we obtain a modified logarithmic transformed IL(MLTIL)distribution.Many researchers used the LT method to propose a new continuous distributions by taking the baselineH(x)of any known distribution.[9,10]introduced a generalizations for modified Weibull extension and generalized exponential distributions,respectively.[11]introduced a logarithmic inverse Lindley distribution by taking theH(x)in(3)of the inverse Lindley distribution.Also,the logarithm transformed Fréchet distribution by[12].The overall motivations to propose the MLTIL distribution are
1.To develop different shapes for the PDF and hazard rate function.
2.To increase the flexibility of the traditional IL distribution in modelling different phenomenons.
3.To model skewed data which can not be modeled by other traditional models.
4.To increase the flexibility of the traditional IL distribution properties like mean,variance,skewness and kurtosis.
5.Two applications showed that the MLTIL distribution provides a better fit than the traditional IL distribution and some of its generalizations.
6.Another motivation to this article is to use six classical estimation methods to estimate the parameters in order to recommend which method provide the best estimates based on mean square error criteria and via a simulation study.
The hazard rate function of the MLTIL distribution can has decreasing or upside-down shapes depending on its shape parameters which makes the distribution is quite effectively in modelling lifetime data.It can be used as an alternative to IL and inverse Weibull distributions.Simulation results reveal that the Anderson-Darling(AD)estimators perform better than other estimators in terms of minimum mean-squared errors.Finally,the analysis of engineering and medical data sets show the ability of the MLTIL distribution to provide a better fit than some other competitive models.The rest of the paper is organized as follows:In the next Section we describe the MLTIL distribution and a mixture representation of its density.Some of its statistical properties are discussed in Section 3.Six classical estimation methods are considered in Section 4.A simulation study is conducted in Section 5.Two applications are considered in Section 6.In Section 7,the paper is concluded.
2 Model Description
In this section we introduce the MLTIL distribution.Let the random variableXfollows the IL distribution with PDF and CDF,respectively,given by(1),(2),then from(1)–(3)the PDF of the MLTIL distribution is given by
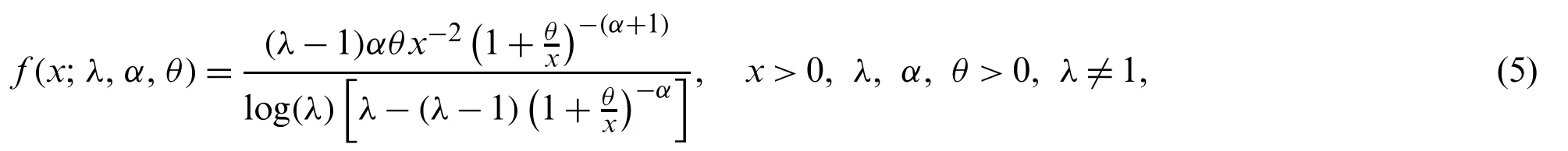
and its CDF is

The survival function(SF)is given by

and the hazard rate functions is
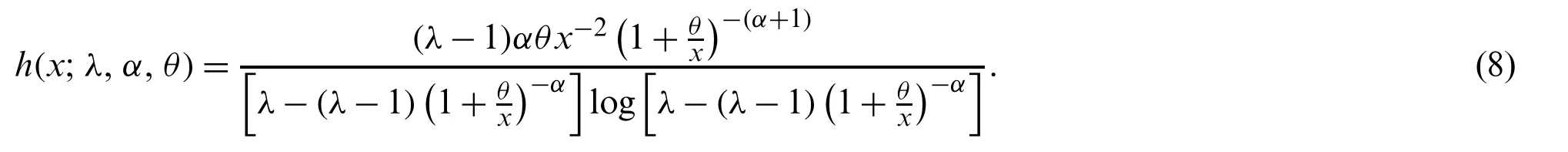
For some selected values of the parametersλ,αandθ,Fig.1 indicates the various shapes of the PDF of the MLTIL distribution,while Fig.2 shows the different shapes of the hazard rate function.These Figure indicate the flexibility of the MLTIL distribution to model right skewed data as well as the data with decreasing and upside down bathtub shaped.

Figure 1:Plots of the MLTIL density for different values of λ, α and θ
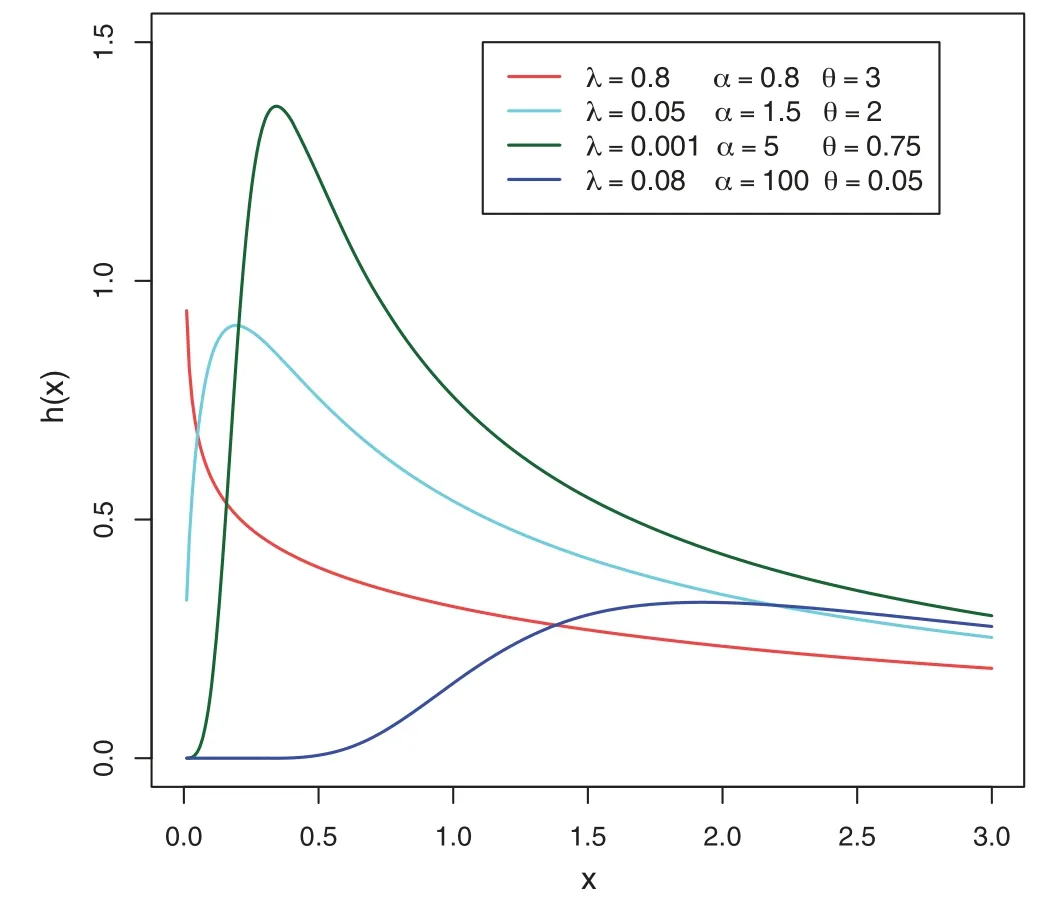
Figure 2:Plots of the MLTIL hazard rate function for different values of λ, α and θ
Now,we can obtain an useful representation for the PDF and CDF of the MLTIL distribution.Using the series representation in the form

Applying(9)for the PDF in(1),we can obtain

whereh(x;α(k+1),θ)denotes the PDF of the IL distribution with scale parameterθand shape parameterα(k+1)and

Different structural properties of the MLTIL distribution can be determined using this representation.By integrating(10),the CDF ofXis given by

whereH(.)is the CDF of the IL distribution with scale and shape parametersθand shape parameterα(k+1),respectively.
3 Properties of the MLTIL Distribution
In this section some statistical properties of t he MLTIL distribution are obtained including quintile function,moments,incomplete moments,conditional moments and entropies.
3.1 Quantile Function
For the MLTIL distribution the quantile function,sayx=QMLTIL(q),can be obtained by inverting(6)as

We can easily generateXby takingqas a uniform random variable in(0,1).Based on(12),one can compute the measures of skewness(Sk)and kurtosis(Ku)as follows:

and

respectively,whereQ(·)refers to the quantile function.
3.2 Moments
Thenth moment of MLTIL distribution can be derives as


whereB(a,b)is the beta function,Γ(0)=−γanddenotes Euler’s constant andFor more details see[13].Similarly,for the MLTIL distribution we can obtain thenth inverse moment as follows:

In particular,

whereγdenotes Euler’s constant.

and

Therth central momentμrofXis derived as

The Sk and Ku measures can be computed using the following expressions:

The following propositions are a description of three different types of moments such as incomplete moments,moment generating function(mgf)and conditional moment.
prop 3.1.IfX~MLTIL,then the incomplete moments ofXis given as follows:

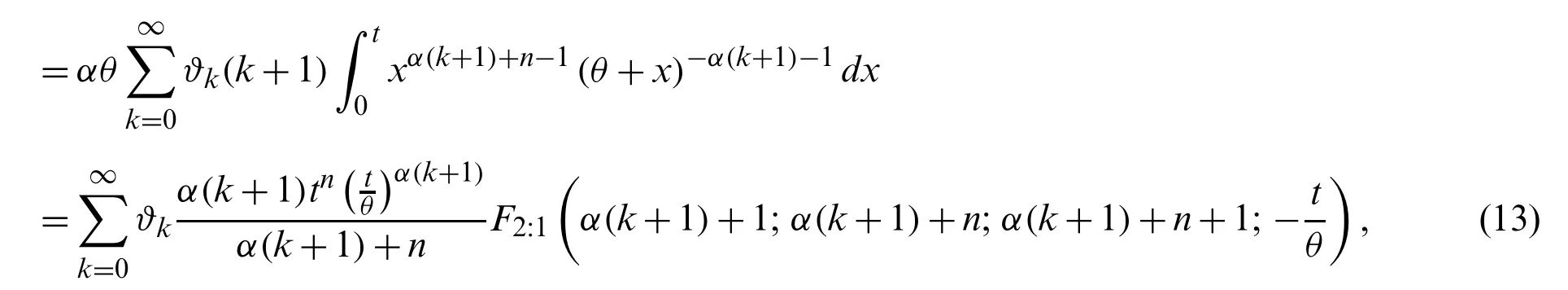
The first incomplete moment,I1(t),follows from Eq.(13)withn=1.
prop 3.2.IfX~MLTIL,then the mgf ofXis

prop 3.3.IfX~MLTIL,then the characteristic generating function(cgf)ofXis

prop 3.4.IfX~MLTIL,then the conditional moment ofXis

where

3.3 Entropies
Entropy has been used in areas like in physics(sparse kernel density estimation),medicin(molecular imaging of tumors)and engineering(measure the randomness of systems).The entropy is a measure of variation of the uncertainty.The R´enyi entropy(RE)of orderρis defined as

For the MLTIL distribution in(1),we can write

Theρ-entropy,Hρ−R(x),can be written as

Shannon’s entropy(SE)is defined asE[−logf(X)]and it is a special case of(15)forρ↑1.Limitingρ↑1 in(15)and using L´Hospital´s rule,one obtains

3.4 Distribution of Order Statistics
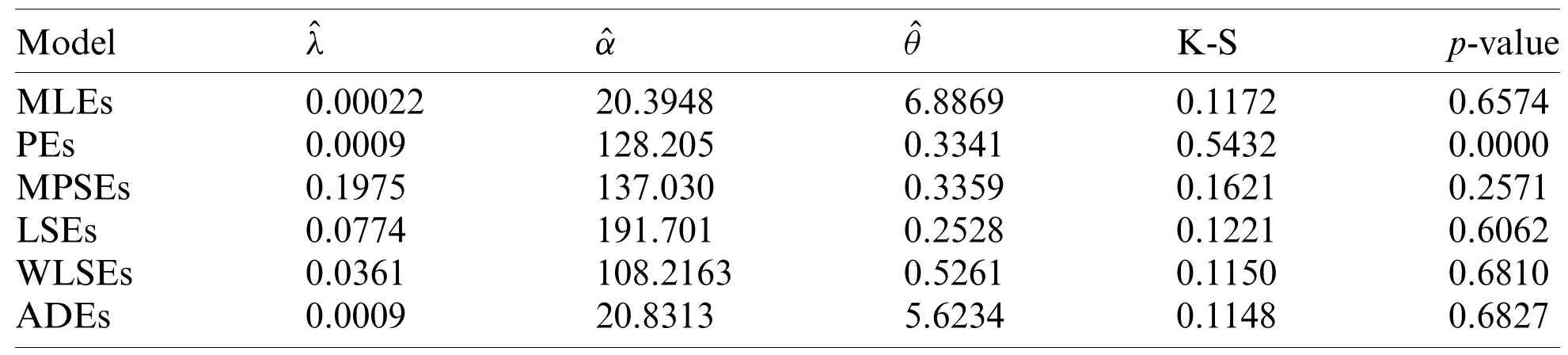
LetX(1) whereB(.,.)is the beta function.Using(1),(6)and a power series expansion,we obtain From(17)and(16),we can write Particularly,we can obtain the PDF of the first and last order statistics from(18),respectively,as and The(u,v)th probability weighted moments of the random variableXis defined by Based on Eq.(21),we can obtain the probability weighted moments of the MLTIL distribution as where Thenth moment of the residual life(RL)of the random variableXis defined as follows Based on Eq.(1)and applying the binomial expansion of(x−t)n,we have Thenth moment of the reversed RL can be derived using the general formula Based on Eq.(1)and applying the binomial expansion of(t−x)n,we can write LetY1~MLTIL(λ1,α1,θ1)andY2~MLTIL(λ2,α2,θ2).IfY1represents stress andY2represents strength,then the stress-strength parameter,denoted byR,for the MLTIL distribution is given by Using series expansion in the last equation,we obtain In this section,six estimation methods are considered to estimate the MLIIL distribution parameters. Using a random sample of sizemtaken from the MLTIL distribution,then based on(5)the log-likelihood function can be written as whereϖ=(λ,α,θ)T.The maximum likelihood estimates(MLEs)ofλ,α,andθ,denoted byare the solution of the following three equations It is observed that these equations cannot be solved analytically forλ,α,andθ,therefore to obtainandθMLone can use any numerical technique for this purpose. Kao et al.[18,19]originally proposed the percentile method of estimation and recently used by many authors to obtain the parameters of some proposed distributions,see for example[20,21].It is very useful when the distribution has a closed form quantile function.Since the MLTIL distribution has an explicit quantile function as in(12),then we can obtain the percentile estimates(PEs)ofλ,α,andθ,denoted byandby minimizing wherex(j)is the ordered observation ofxj,j=1,...,nandqj=j/(m+1).Instead of minimizing(25)with respect toλ,α,andθ,we can obtainandby solving and where and Cheng et al.[22,23]introduced the method of maximum product of spacing(MPS)to obtain the estimates of the continuous univariate distributions parameters as an alternative to the method of maximum likelihood.LetΨi(ϖ)is the uniform spacing defined as follows: To obtain the MPS estimates(MPSEs)ofλ,α,andθ,denoted byandwe can maximize the following function with respect toλ,α,andθ.Instead of maximizing(26)to obtainandwe can solve the following three equations to obtain these estimates where and Swain et al.[24]considered the least squares(LS)and weighted least squares(WLS)methods to estimate the beta distribution parameters.The LS estimates(LSEs)ofλ,α,andθ,denoted byandcan be obtained by minimizing with respect toλ,α,andθ,whereηj=1−j/(m+1).The estimatesandcan be also obtained by solving and whereδ1j(x(j)|ϖ),δ2j(x(j)|ϖ)andδ3j(x(j)|ϖ)are given by(27),(28).Similarly,the WLS estimates(WLSEs)ofλ,α,andθ,denoted byandcan be computed by minimizing with respect toλ,α,andθ,whereAnother way to obtain these estimates is to solve the following equations: and whereδ1j(x(j)|ϖ),δ2j(x(j)|ϖ)andδ3j(x(j)|ϖ)are given by(27),(28). The AD method of estimation is a type of minimum distance estimator which obtained by minimizing an AD statistic.The AD estimates(ADEs)ofλ,α,andθ,denoted byandcan be obtained by minimizing with respect toλ,α,andθ.Another way to obtain these estimates is to solve the following equations: whereδ1j(x(j)|ϖ),δ2j(x(j)|ϖ)andδ3j(x(j)|ϖ)are given by(27),(28). We cannot compare the performance of the different proposed estimators theoretically,therefore a simulation study is done in order to show the behavior of the various estimators in terms of mean square error(MSE)criteria.To conduct the simulation study,we choose two sets of the parameters values;Set I:(λ,α,θ)=(1.5,0.5,0.5)and Set II:(λ,α,θ)=(0.5,2,2).Also,different sample sizes are chosen,wherem=20,50,100,150,200 and 250.These values are selected to indicate the affect of the small,moderate and large sample sizes in the accuracy of the estimates.Each setting is replicated 1000 times and the average estimates and average MSEs are obtained.These values are tabulated for Sets I and II in Tabs.1 and 2,respectively.The results in these Tables show that the MSEs decrease as the sample size increases in all the cases,which means hat these estimators are consistent.It is also observed that the MSEs tend to zero except the PEs especially in the small and moderate sample sizes.Comparing the performance of the different estimates in terms of minimum MSEe,we can conclude that the ADEs perform better than other estimates in most of the cases.Based on these results,we recommend to use the Anderson-Darling method to estimate the MLTIL distribution parameters. Table 1:Estimates and MSEs for different estimates of λ=1.5 and α=θ=0.5 Table 2:Estimates and MSEs for different estimates of λ=0.5 and α=θ=2 Table 3:Real data sets To show the applicability of the proposed distribution and the different estimators derived in the previous sections two real data sets are analyzed.The first data set considered by[25]which represent life times(in days)of 39 liver cancers patients taken from Elminia cancer center Ministry of Health in Egypt.The second data set consists of 29 time between failures of a piece of construction equipment in chronological studied by[26].These data are displayed in Tab.3. We compare the results of the MLTIL distribution with IL distribution,inverse Weibull(IW)distribution,APIL distribution by[7]and alpha power inverse Weibull(APIW)distribution by[27].The density functions of these distributions(forx>0)are as follow and We first obtain the MLEs of the competitive distributions.These estimates are presented in Tabs.4 and 5 for datas 1 and 2,respectively.To compare the performance of the difference distributions to fit the data set,we use Kolmogorov-Smirnov(K-S)distance and the correspondingp-value.These statistics are also presented in Tabs.4 and 5 for datas 1 and 2,respectively.From the results in these Tables it is observed that the MLTIL distribution has the smallest K-S distance with the highestp-value among other competitive distributions,therefore we conclude that the MLTIL distribution is the suitable model to fit these data.The fitted PDF,CDF,SF and P-P plot of the MLTIL distribution are presented in Figs.3 and 4 for datas 1 and 2,respectively.These Figures support the results discussed before that the MLTIL distribution provides a close fit to these data sets. Figure 5:Histogram and the fitted MLTIL density using different estimation methods for(a)data 1 and(b)data 2 Table 6:Various estimates,K-S and p-value of real data 1 Table 7:Various estimates,K-S and p-value of real data 2 Figure 3:Fitted density,estimated CDF and SF,and P-P plots for real data 1 Figure 4:Fitted density,estimated CDF and SF,and P-P plots for real data 2 Table 4:MLEs,K-S and p-value of real data 1 Table 5:MLEs,K-S and p-value of real data 2 To see which estimation method provide a good fit to these data we compare the other estimation methods with the maximum likelihood methods based on K-S distance and itsp-value.For the two data sets,the various estimates,K-S distance and itsp-value are obtained in Tabs.6 and 7,respectively.Comparing the fitting of the different methods we can observe that the ADEs provides a good fit based on minimum K-S distance with highestp-value.Therefore,we can recommend to use the AD method to estimate the MLTIL distribution parameters from these real data sets.Also,the histogram and the fitted MLTIL distribution based on the different methods are presented in Fig.5 for the two data sets. In this paper,we have considered and studied a new generalization of the traditional inverse Lomax distribution by adding a new shape parameter.We have used the logarithmic transformed method for this purpose and a new three parameters inverse Lomax distribution which called modified logarithmic transformed inverse Lomax distribution is introduced.The new distribution has different failure rate shapes,so it can be used in analyzing lifetime data.Some statistical properties of the new distribution are derived including quantiles,moments,probability weighted moments,entropies,residual life,stress-strength parameter and order statistics.To estimate the parameters of the proposed distribution,six classical methods are considered.To compare the efficiency of these methods a simulation study is performed and the performance of the different estimators is compared.To show the applicability of the new distribution,two real data sets are analyzed which indicate that our new distribution perform better than some other competitive distributions.Also,the numerical illustration revealed that the Anderson Darling estimation method is the best method to estimate the proposed distribution parameters.In this study,the proposed distribution shows its ability in modelling engineering and medical data sets where traditional and some recently proposed models cannot be used for this purpose.We hope that this model attract wider sets of applications in the other different fields. Acknowledgement:The author would like to thank the editor and the two reviewers for their constructive comments which improve the quality of the paper. Funding Statement:This project was funded by the Deanship Scientific Research(DSR),King Abdulaziz University,Jeddah under Grant No.(RG-14-130-41).The author,therefore,acknowledge with thanks DSR for technical and financial support. Conflict of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.




3.5 Probability Weighted Moments



3.6 Residual Life and Reversed Failure Rate Function

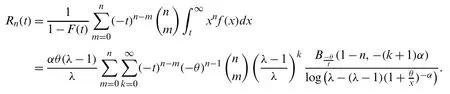
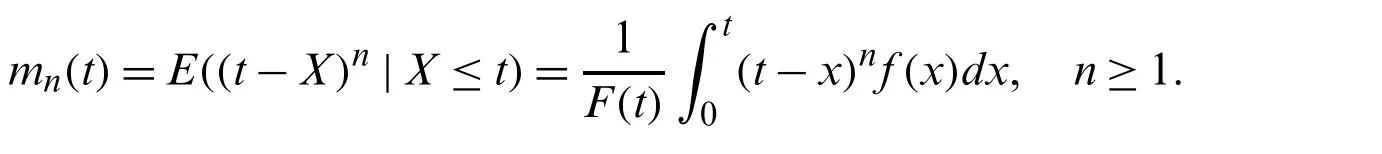
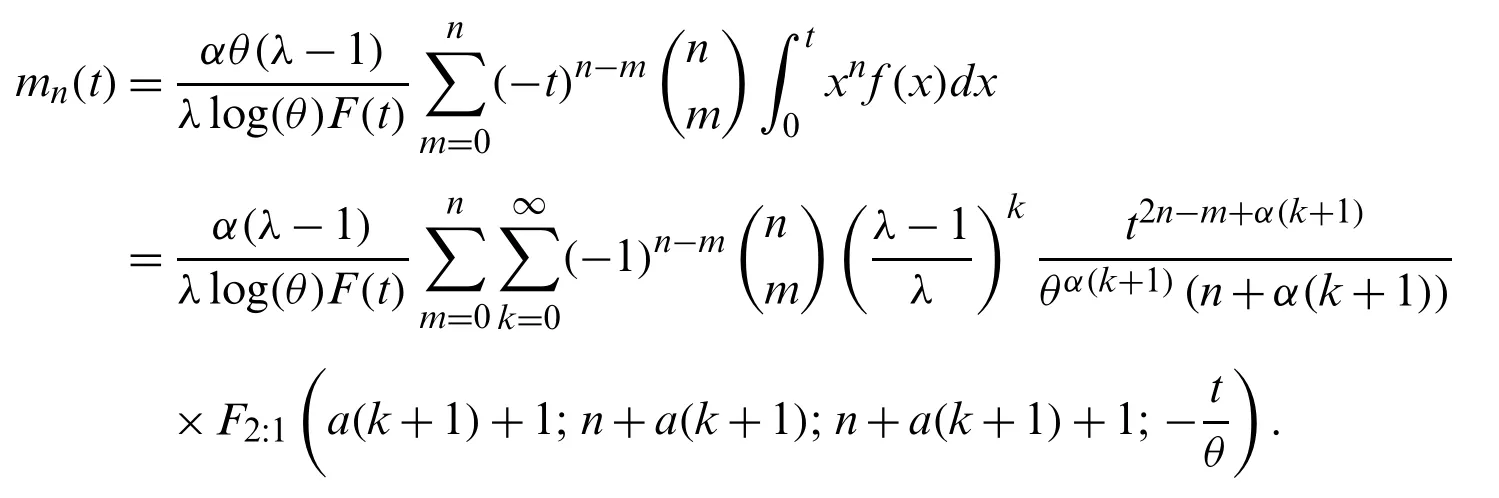
3.7 Stress-Strength Model
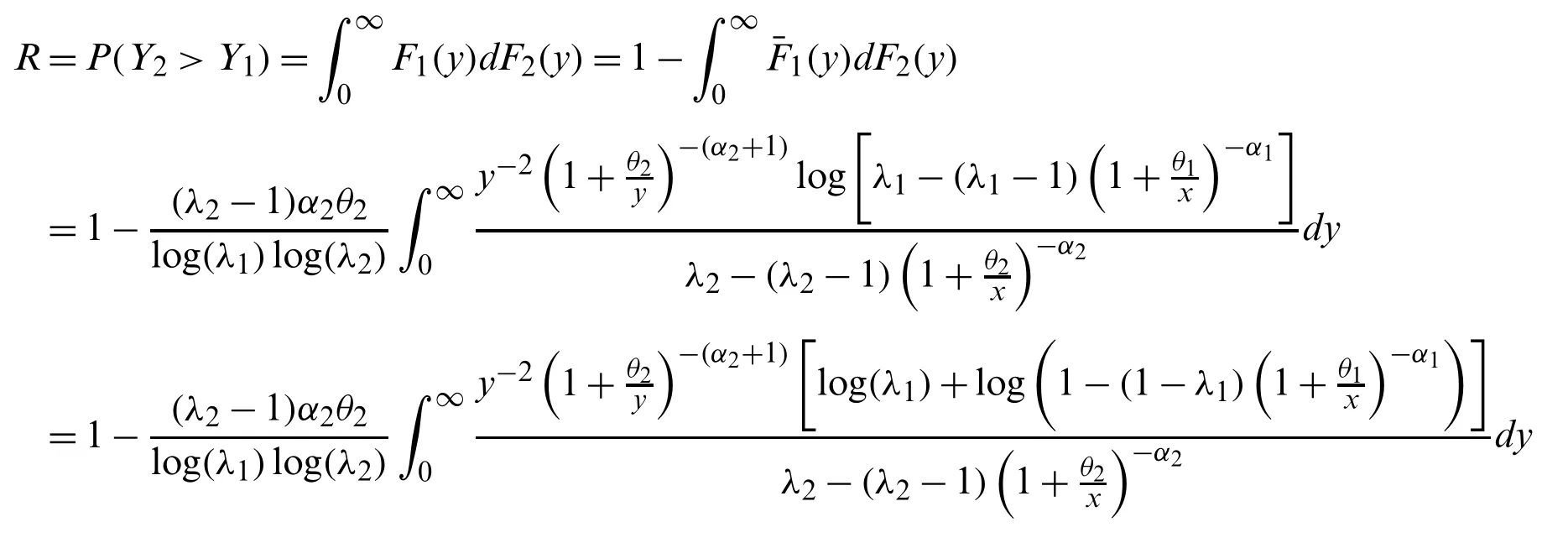


4 Estimation
4.1 Maximum Likelihood Estimation
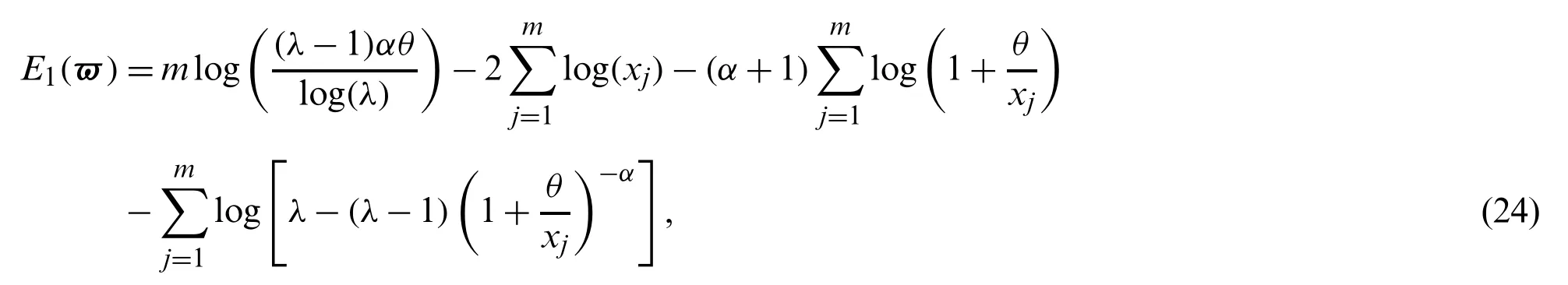

4.2 Percentile Estimation





4.3 Maximum Product of Spacing Estimation
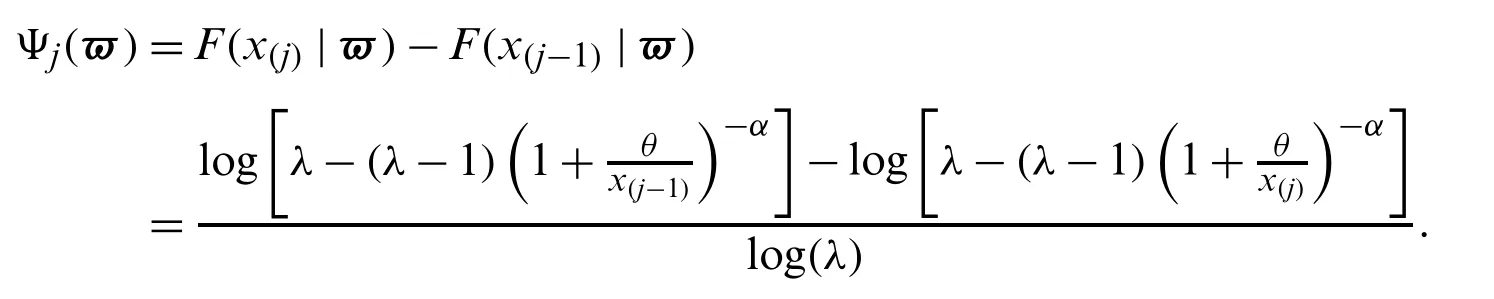


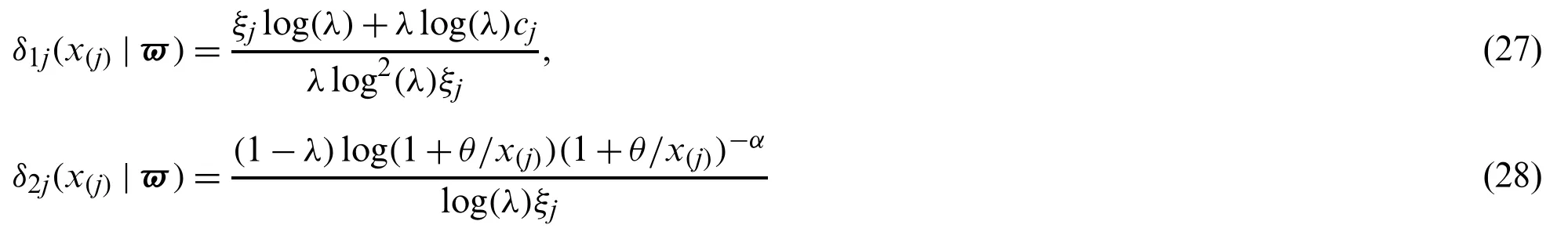

4.4 Least and Weighted Least Squares Estimation
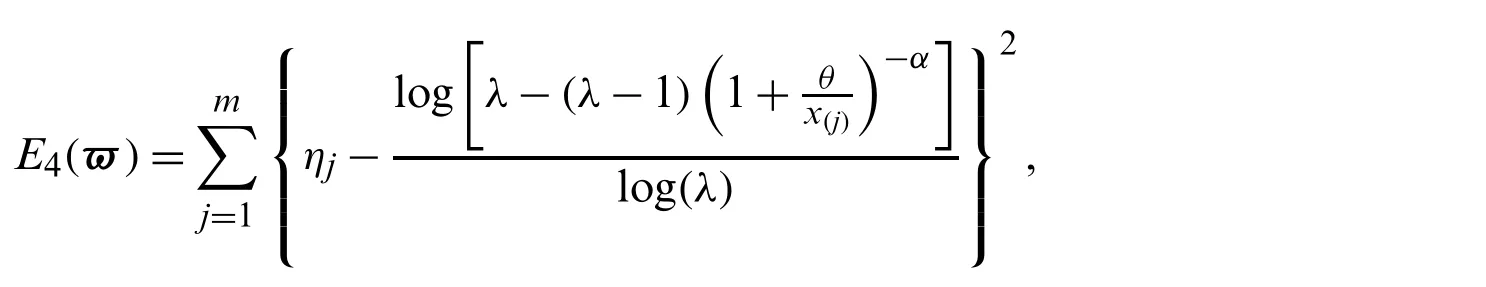






4.5 Anderson-Darling Estimation

5 Simulation Study



6 Applications
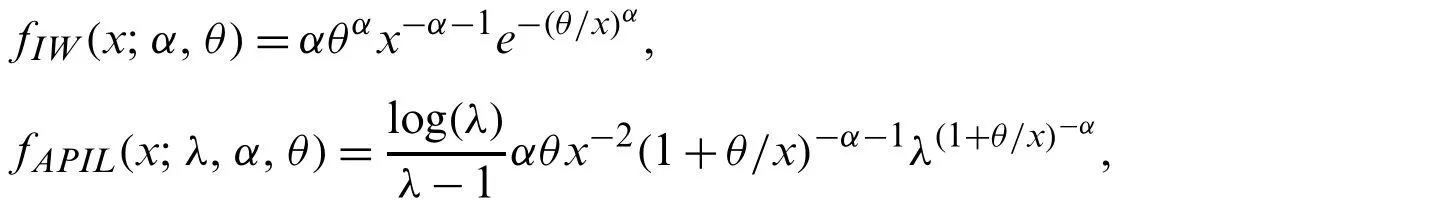

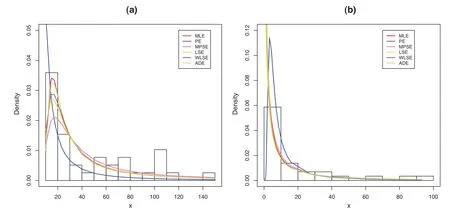





7 Conclusion
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Real-Time Integrated Face Mask Detector to Curtail Spread of Coronavirus
- Introduction to the Special Issue on Computer Modelling of Transmission,Spread,Control and Diagnosis of COVID-19
- Bubble-Enriched Smoothed Finite Element Methods for Nearly-Incompressible Solids
- Laminar and Turbulent Characteristics of the Acoustic/Fluid Dynamics Interactions in a Slender Simulated Solid Rocket Motor Chamber
- A Double-Phase High-Frequency Traveling Magnetic Field Developed for Contactless Stirring of Low-Conducting Liquid Materials
- Quadratic Finite Volume Element Schemes over Triangular Meshes for a Nonlinear Time-Fractional Rayleigh-Stokes Problem
