基于六维力传感器的机器人本体碰撞点检测研究

王志军 刘 璐 李占贤

(1.华北理工大学机械工程学院， 唐山 063210； 2.河北省工业机器人产业技术研究院， 唐山 063210)

0 引言

共融机器人是下一代机器人的发展目标，实现人机共融的首要问题是安全[1-4]。在机器人作业过程中，为了保证人、机、物的安全，需要对作业环境信息进行感知，而力信息和机器人碰撞点的位置检测是其中的重要部分。为此，越来越多的传感器被集成到机器人系统中[5-9]；这些传感器可协助机器人获取环境信息，有助于机器人作出正确判定[10-14]。视觉传感器协助机器人获取环境的外观信息，用于实现目标跟踪和物体捕获等[15-17]。碰撞感测也是一种重要的环境感测方法，通过该方法机器人感测碰撞点和碰撞方向，以免再次发生碰撞，并实现对机器人的反馈控制。在包含人和机器人的环境中，碰撞感知对避免严重碰撞至关重要[18-21]。贴在机器人整个表面上的皮肤力传感器(如人体皮肤系统)可以感应力作用点、方向和大小。麻省理工学院研究了一种称为QTC(量子隧道复合材料)的特殊复合材料，该材料受到金属和非金属的挤压时[22-23]，传感器可通过电阻变化测量力信息。与之相类似的还有由并五苯分子和电子皮肤组成的有机薄膜等。皮肤力传感器价格昂贵、易损坏、设计复杂、对环境要求较高、采样率低、通用性较差[24-26]，难以在现实中使用。皮肤传感器的灵敏度系统无法获得碰撞方向信息，并会受到许多因素的影响，例如温度和湿度等。在利用力传感器进行碰撞点检测方面，文献[27]基于力/力矩传感器和结构化的探针建立一种物体轮廓探测方法，文献[28]基于力/力矩传感器数据和机械手指端几何模型提出求解触点位置的方法。已有研究主要针对结构化碰撞过程中没有形变产生的碰撞点进行识别，若碰撞体表面为非规则形状或建模较难，则已有的方法应用较为受限。

按照碰撞点和碰撞外力的不同，机器人本体碰撞大体可以分为单点单外力碰撞、单点外力/外力矩混合碰撞、多点外力碰撞、多点外力/外力矩混合碰撞等。多点多外力/外力矩的碰撞可以视为单点单外力的特殊组合形式。

针对皮肤力传感器对机器人碰撞点检测的不足，本文提出一种利用基座处六维力传感器采集信息进行自约束，从而对机器人本体碰撞点进行检测的方法。在对基座处六维力传感器进行动态力补偿后，运动过程中机器人数值在零点附近波动，当传感器数值超过一定阈值后即可认为机器人与外界发生碰撞，对经过补偿后的传感器每帧数据进行自约束，可计算出机器人本体碰撞点坐标。

1 碰撞点检测模型

与传统的应用六维力传感器不同，为了实现对机器人本体的碰撞位置检测将机器人安装在基座处。传感器的安装位置示意图如图1所示。

六维力传感器可以测得力和力矩在3个轴上的分量信息，假设基座处传感器采集了F(Fx,Fy,Fz)和M(Mx,My,Mz)，则碰撞点的位置信息表示为

M=PF

(1)

式中P(Px,Py,Pz)为碰撞点相对于传感器坐标系的位置矢量。式(1)可以改写为

(2)

由于|F|=0，所以碰撞点的位置解并不唯一，这时需要利用其他约束条件来确定碰撞点的位置。

将传感器采集到某一帧的数据代入式(2)可以得到1条外力作用矢量线Lc(p)，其表达式为

(3)

传感器每帧采集的不同参数决定了不同的外力矢量线，在实际中碰撞外力的方向大多数与机器人的运动方向存在一定夹角，因此利用传感器不同帧数计算的外力矢量线在空间中会相交于某点Pc，该点即为碰撞点，具体计算方法为

{P(x,y,z)|(x,y,z)∈Lc1(p)∩Lc2(p)}

(4)

由于传感器存在的测量误差会使得计算的空间力矢量线在空间中不会相交在碰撞点，但在某一平面内的投影会相交于正式的碰撞点在该平面的投影附近。所以可以通过投影法先求得外力矢量线在平面的交点，再将交点坐标代入原始方程求得碰撞点信息，如图2所示。

假设L′XOY是Lc(p)在XOY平面的投影直线，在XOZ平面的投影为L′XOZ，在YOZ平面的投影为L′YOZ，计算式为

(5)

图2中P′(x,y)是2条外力矢量线的投影L′XOY，1和L′XOY，2的交点，P1、P2为投影交点在外力矢量线上的对应点，P1、P2计算式为

(6)

式中η——确定最佳投影平面的选择因子

投水平面选择规则为

(7)

其中

(8)

式中θXOY、θXOZ、θYOZ——外力矢量线在XOY、XOZ、YOZ平面投影L′XOY，1和L′XOY，2的夹角

若XOY平面为最优投影平面，则P1(x1,y1,z1)和P2(x2,y2,z2)计算公式为

(9)

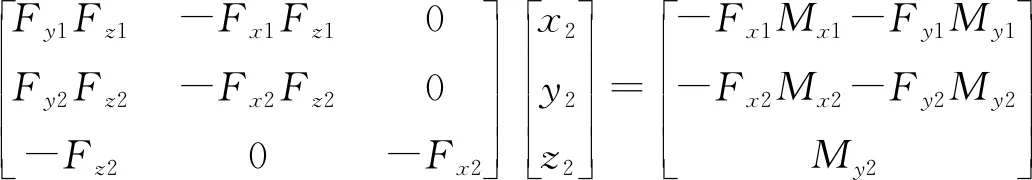
(10)

真实的碰撞点坐标在两点附近，但精确位置无法计算，因此初步判定碰撞点P为两点的中点，即

(11)

在机器人碰撞瞬间传感器可以采集到多组数据，求解的空间外力矢量线示意图如图3所示。为了在多组计算结果中搜索出和真实碰撞点最近的最优解，假设ζ(ζMx,ζMy,ζMz)为误差因子，P″(x″,y″,z″)为初步计算的碰撞点坐标。可得

(12)

2 动态力补偿算法

将六维力传感器安装在机器人基座处时应首先消除机器人本体的重力和运动过程中末端负载对传感器的影响，应对传感器进行动态力补偿。在传感器上执行动态力补偿后，当机器人处于运动状态且不受外力作用时，读数将恒定为零。若传感器读数超过阈值，即认为机器人与外界意外碰撞。 机器人重力补偿如图5所示。

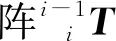
(13)

由式(13)可得

(14)

将机器人各连杆参数代入式(13)中，可依次得到相邻连杆之间的位姿变换矩阵。坐标系{i}相对于坐标系{0}的变换矩阵为

(15)

假设关节i的质心ci相对于关节坐标系i的位置矢量为

ci=[cixciyciz]T

(16)

各连杆质心坐标系{ci}相对于{0}系的齐次变换矩阵为

(17)

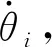
(18)

(19)

(20)

(21)

可以对连杆之间建立动力学方程

(22)

(23)

ri,ci——关节i上附着的坐标系原点Oi到质心ci的矢径

ri+1,ci——关节i+1上附着的坐标系原点Oi+1到质心ci的矢径

Ii——杆i相对于其质心ci的惯性张量

(24)

将基座处的受力信息经过式(24)进行坐标变换即可得到基座处六维力传感器最终所需要的重力补偿数值，即Sf和SM。若机器人处于某一位姿时，基座六维力传感器的力/力矩传感器读数分别为Df和DM，则经过重力补偿后的力/力矩信息F和M为

(25)

经过动态力补偿后，在运动过程中没有外力的情况下，机器人可以使六维力传感器的读数恒定为零。一旦基座处的六维力传感器的读数超过设置的阈值，就可认为机器人与外部发生碰撞。机器人与外界之间的碰撞是一个连续的过程，因此，在动态力补偿后，基座上的传感器读取的每一帧数据都可以用作碰撞点检测算法的输入。

在经过对数据的动态力补偿以后，判断发生碰撞与否的阈值确定与机器人的整体结构参数、末端负载情况、传感器的精度等情况有关。因此增加S作为安全阈值的判断环节，S取值0或1。当S=0时机器人与外界不发生碰撞，机器人正常工作，S=1是继任为机器人与外界发生碰撞[29]。表达式为

(26)

通常情况下结合机器人实际情况进行人为设定，为了提高碰撞识别的精度，选择了每个方向最小的力误差作为识别是否发生碰撞的阈值，即δf=0.492 3 N。

3 仿真实验

为了验证本文提出的动态力补偿算法和碰撞点检测算法的有效性和精度，构建了1个3自由度机器人模型进行仿真实验，如图7所示。

为了减少计算量，机械手的连杆和关节中心对称，每个连杆的重心位于其自身的中心轴上。表1给出了本文3自由度机器人每个连杆的结构参数，材料为合金，ρ=2.7×103kg/m3。图7中，l1=120 mm,l2=150 mm,l3=200 mm,l4=200 mm,h=30 mm。

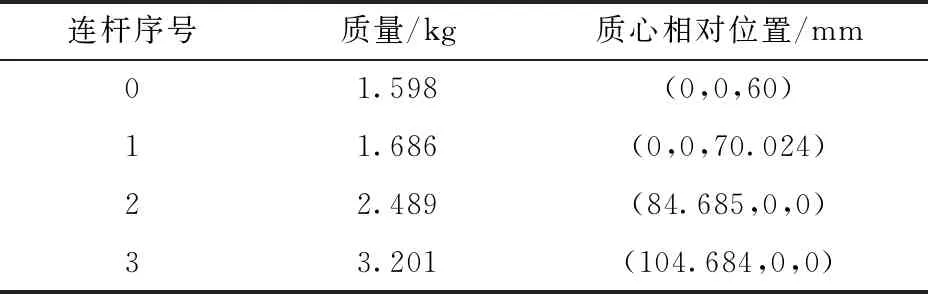
表1 连杆参数

各连杆相对于其质心的惯性张量为

(27)

(28)

(29)

基座处传感器采集的数据随着时间而不断变化，将传感器采集到的数据经过动态补偿处理后作为式(2)的输入进行碰撞点的计算。将机器人模型导入ADAMS，以验证所提出的动态力补偿算法和碰撞点检测算法。实验中模拟施加的碰撞力的大小、方向和位置已知，并且实验结果数据以传感器坐标系为基准。

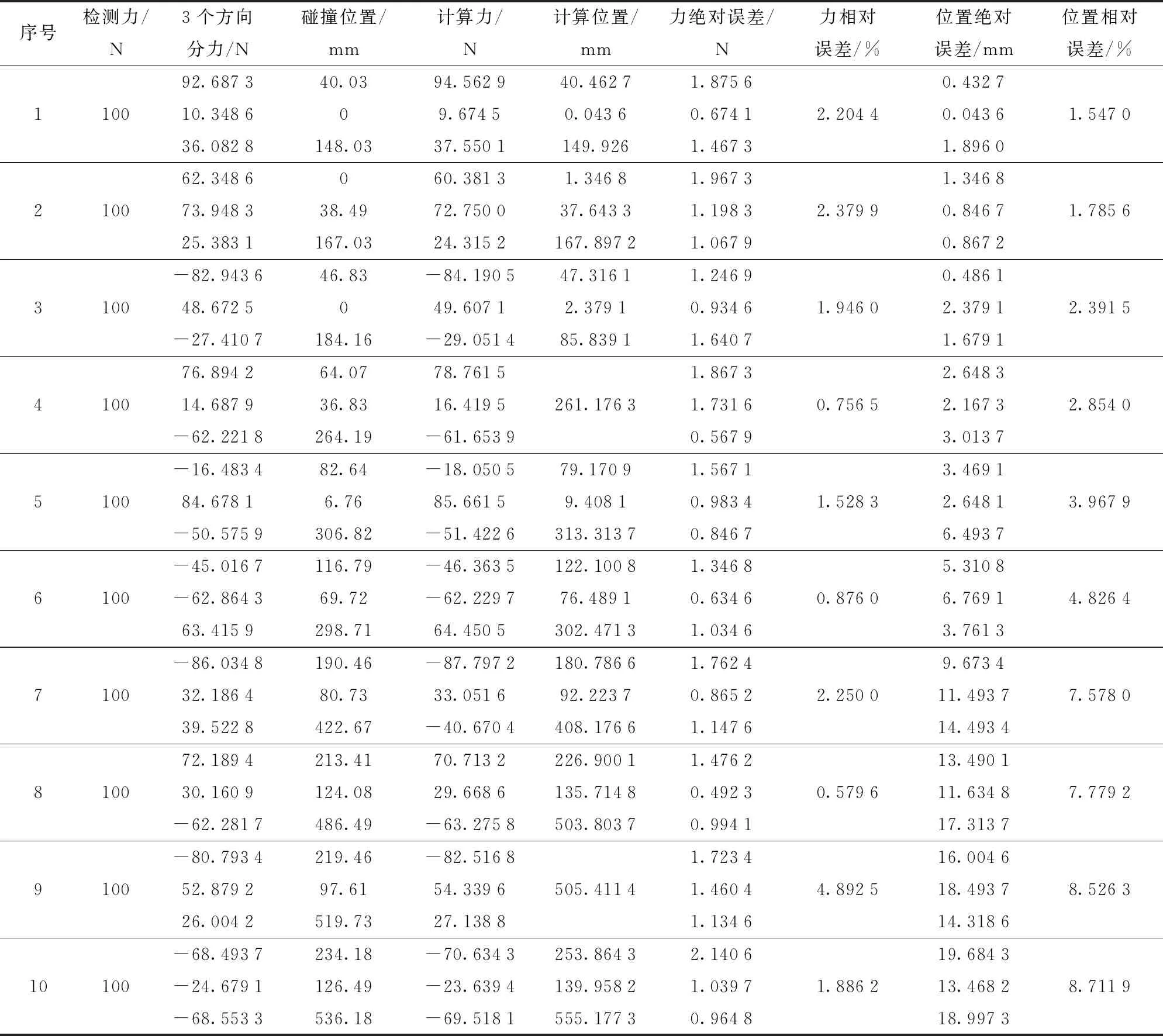
表2 不同碰撞点的实验结果

为了验证提出算法的精度，对实验结果进行了误差分析。

各方向分力的相对误差计算式为

(30)

式中 ΔFn——力在3个方向的绝对误差

|FC|——测量力矢量的模

合力相对误差计算式为

(31)

式中fCx、fCy、fCz——测量力的3个方向分量

fDx、fDy、fDz——计算力的3个方向分量

位置各方向的相对误差计算式为

(32)

位置的相对误差计算式为

(33)

各个方向的分力和位置误差如图8所示。在对数据进行误差计算过程中若分母为0，则计算结果输出为0。

由图8可以看出，当碰撞力恒定时，随着碰撞点距离的变化，各个方向上分力的相对误差在5%以下范围内波动，合力最大相对误差为4.892 5%。但随着碰撞点的距离增加，碰撞位置在各个方向上的绝对误差和相对误差不断增加，在最远处距离力传感器坐标系598.61 mm的位置碰撞点坐标相对误差达到最大值8.711 9%。采用这种方法进行碰撞点检测满足机器人最远点碰撞精度要求。

4 结束语

提出了一种单点单外力机器人碰撞点检测算法，并在此基础上提出了六维力传感器动态力补偿算法。对该算法进行了仿真实验，证明了该算法的有效性，同时表明，动态力补偿算法的精度不会随着碰撞点位置的变化产生明显变化。碰撞点检测算法的准确性受碰撞位置影响，在最远处598.61 mm位置上碰撞点的相对误差最大值为8.711 9%，满足机器人碰撞点检测算法的精度要求。