基于时空特征序列匹配的交通流状态估计方法*

陈佳良 胡钊政 李 飞

（武汉理工大学智能交通系统研究中心 武汉430063）

0 引 言

交通流状态是交通信息服务系统的基础，城市道路实时交通信息是实现交通管理及控制、动态诱导、以及改善道路通行条件的基础。国外对交通流状态的评价主要基于路段速度、道路交通密度、交通量和出行时间等交通运行参数方面；国内北京、上海、广州、深圳、武汉及杭州等地确定了交通运行评价指标,可以归纳为基于拥堵里程比例、出行时间比和综合评价等几种计算方法[1-2]。

为得到交通流状态评价指标值，已有研究提出不同的交通流状态估计方法。根据不同的数据运算方法，将近些年涌现的交通流状态估计方法大致分为3类：①基于数据相关性的方法。如吕北岳[1]通过回归分析，得到了行程时间比与交通运行指数之间的关系曲线；韦伟等[3]利用时空Moran散点图构建了1种基于时空自相关预分类的道路交通状态聚类方法，反映了路网物理结构与交通需求之间的内在匹配关系；张婧[4]、庄广新[5]、Wang Xiangxue等[6]利用时空相关系数将交通流数据的时空相关性引入算法，提高数据参数运算的精度；②基于聚类划分的 方 法 。 如 模 糊 聚 类[7]、Kernel-KNN[8]、谱聚 类[9]、RS-KNN[10]、谱聚类与SVM融合[11]、k-means聚类[12]等；③其他机器学习的方法。如LSTM-RNN[6]、元胞自动机[13]、随机森林[14]、组合最小二乘支持向量机[15]、交互式BP-UKF模型[16]、（SAGA-FCM）-PNN[17]等。

上述研究都对各自城市道路状态估计方法做了详尽描述并有一定程度上的改进与创新，然而数据相关性方法需要根据划分的时段分别对邻接路段的相关性进行训练，相关关系较为复杂；聚类方法与机器学习的方法需要对路网中细粒度时间间隔的交通流数据进行相关运算，对算力的要求较高耗时也较大；同时当面对待估计路段上检测器缺失，没有基础交通参数数据时，以历史交通流动态数据为基础的聚类、机器学习的方法便无法全面应用。对此，Adeyemi J.Fowe等[18]提出了1种求和平均-EMGSS的计算模型，以解决路段数据缺失情况下的流量估计问题。然而该方法根据待估计路段邻接上/下游的流量值进行求和平均后计算，没有考虑到所邻接的路段不同时，其道路参数不同对待估计路段的影响不同。

本文为提高无检测器道路交通流状态估计的准确性，同时保证数据运算的时效性，研究了1种基于时空特征序列匹配的交通流状态估计方法；并在估计过程中引入交通流参数与道路参数、路网拓扑参数等时空多维度参数特征，同时附加时间维度参数，构建城市道路交通流DNA特征进行描述；最后引入WH-KNN的方法对城市道路交通流状态时空特征序列进行匹配。

1 时空特征序列匹配交通流状态估计模型

本研究的技术路线见图1。

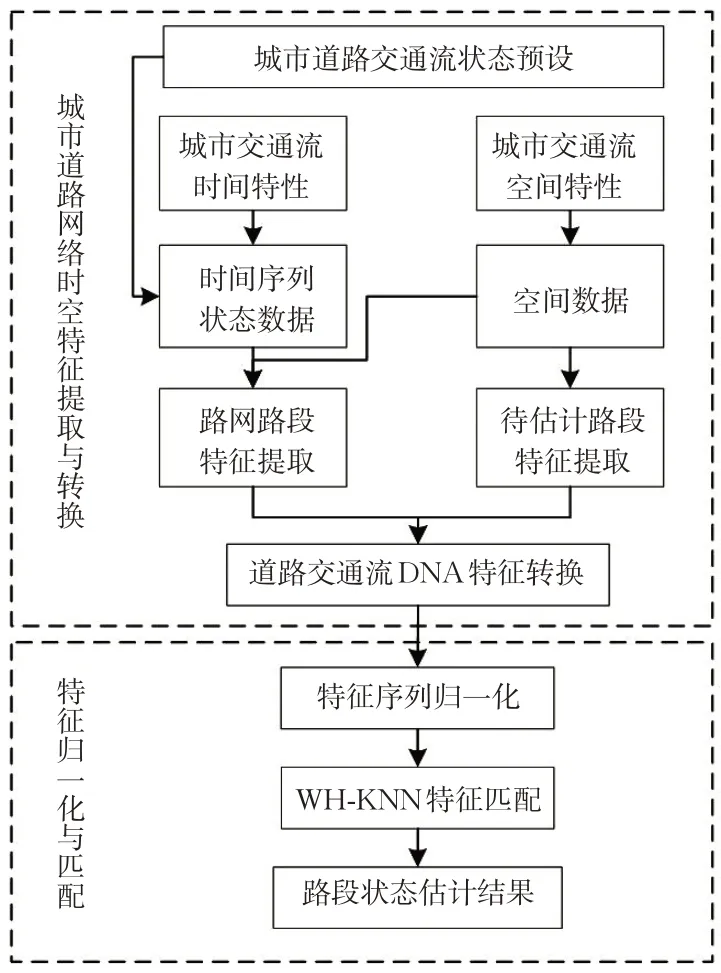
图1 技术路线图Fig.1 Technology roadmap

研究首先进行城市道路交通流状态预设，标定已知数据路段的道路交通流状态；其次，对城市道路网络时空特征进行提取与编码，基于城市道路网络交通流时间与空间特性分析，对待估计路段进行空间拓扑特征的提取，对路网状态预留的路段进行时空特征的提取，并基于所提取的特征，进行道路交通流DNA特征编码，得到路段所独有的道路交通流DNA特征；最后，对道路交通流DNA特征进行归一化与基于WH-KNN的特征匹配，匹配后得到待估计路段状态估计结果。

1.1 城市道路交通流状态预设

交通运行指数（traffic performance index，TPI），是对道路整体运行水平进行量化评估的综合性指标，以0～5评价交通状态的强度，数值越高拥堵越严重。本研究以TPI作为城市路段交通流状态预设指标，其计算方法见式（1）～（3）[1]。

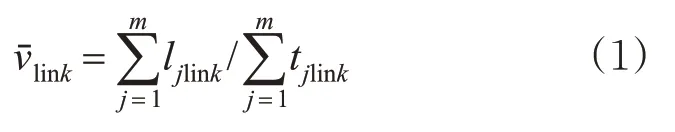
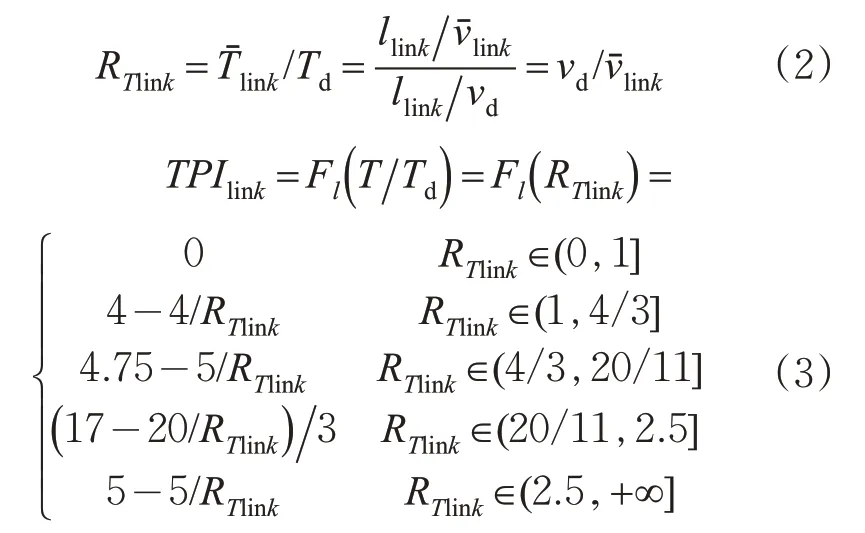
式中：为路段平均车速，km/h；llink为路段长度，m；j为样本车辆编号；m为路段上时间粒度内的样本车辆数，pcu/5min；t jlink为样本车辆通过路段花费的时间，s；RTlink为特定时段内的路段行程时间比；为特定时段内路段上实际出行时间，s；Td为期望车速vd下的出行时间，s；TPIlink为特定时段内路段交通运行指数；Fl(·)为换算关系。其中，一般认为凌晨时段车辆处于期望车速v d状态，应根据城市当地的实际情况界定具体范围。

描述城市道路交通流状态的指标即为TPI所对应的等级，其范围见表1。

表1 道路交通运行指数分级Tab.1 Classification of traffic circulation indices

1.2 基于多维信息的交通流状态特征提取与编码

1.2.1 多维度时空特征提取

针对交通流时空特性分析，不同的文献给出了不同的分析参数。韦伟等[3]、庄广新[5]、Wang Xiangxue等[6]、Xu Dongwei等[8]、商 强 等[10]、Lin Xiaohui[11]、Dai Yihong等[12]、Zhao Shuxu等[14]采用道路流量作为分析参数；吕北岳[1]、韦伟等[3]、张婧[4]、Xu Dongwei等[8]、Yang Senyan等[9]、商 强等[10]、马勇[13]考虑了道路速度的因素；韦伟等[3]、崔 玮[7]、商 强 等[10]、Lin Xiaohui[11]则 考 虑 了占 有 率 ；吕 北 岳[1]、Wang Jingfeng等[2]、Lin Xiaohui[11]采用行程时间作为分析参数；黄振盛等[15]、Adeyemi J.Fowe等[18]及张婧等[19]结合上下游数据进行城市交通流的分析；Ma Shiyong等[20]将不同等级道路列入影响因素。结合上述文献及实际数据情况，本研究以3个维度、8个特征、1个附加维度的方式划分城市道路时空特征，将城市道路网络运行基本参数分为路段参数、交通参数及路网拓扑参数3个维度，其中，路段参数包含道路等级、路段长度、路段车道数3个特征；路网拓扑参数包含邻接层级、邻接路段数2个特征；交通参数包含路段流量、路段平均速度、道路交通流状态3个特征。同时，考虑城市道路交通流随时间变化的特征，故在本研究中共有9个描述特征。路网拓扑时空特征序列划分层次结构见图2。该划分方式基于城市道路网络交通流时空特性分析，在时间维度上，考虑时间序列及其对应的交通流量、速度、状态，属于动态特征；在空间维度上，考虑道路自身属性与路网拓扑属性，属于静态特征。

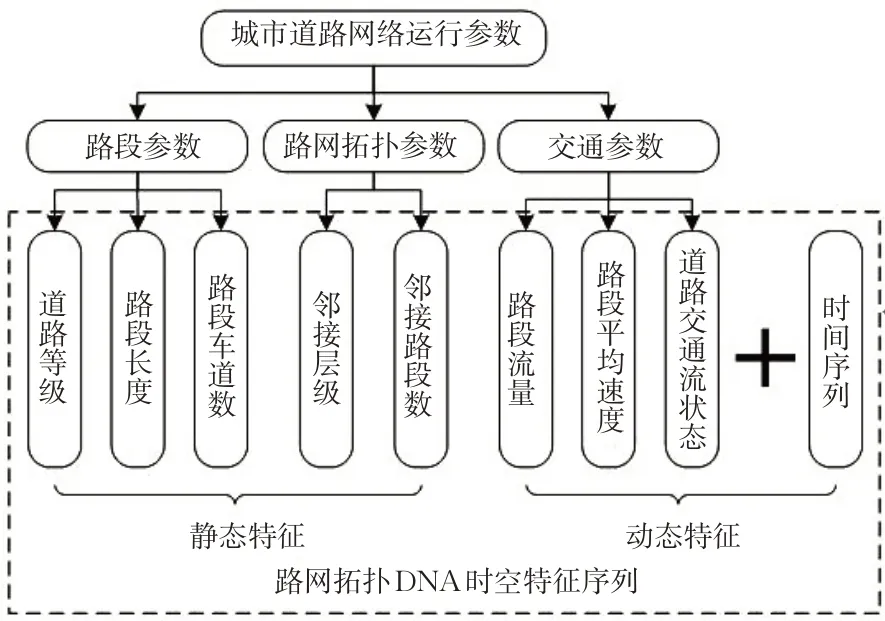
图2 城市道路网络时空特征序列划分Fig.2 Division of temporal-spatial characteristic sequences of urban road network

黄振盛等[15]采用相关系数ri来描述交通流量的相关性，计算公式为

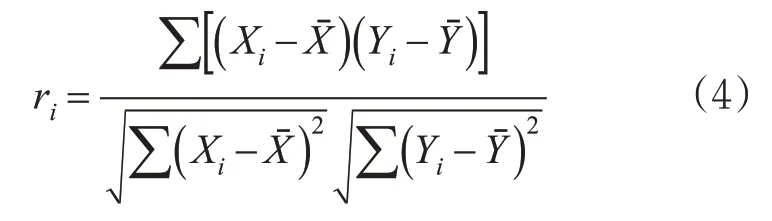
其通过实例证明，空间一级道路参数与预测交通流量数据的相关系数为0.63，具有强相关性。因此，本研究在邻接层级部分采用路网拓扑中一级相邻的路段作为特征，即邻接层级标记为1。其他特征依据相应的时空特性实时计算选取。

1.2.2 道路交通流DNA特征编码

DNA是人体遗传的基本载体，人类的染色体是由DNA构成的，人体约有30亿个碱基对构成整个染色体系统，而且在生殖细胞形成前的互换和组合是随机的，所以世界上没有任何2个人具有完全相同的30亿个核苷酸的组成序列。在城市道路交通运行系统中，由于人们出行行为的随机性，道路上的车辆产生也是随机的，因此在每个时间粒度内，城市道路交通流都会产生各自独特的特征。Liu Zhe等[21]通过此方法描述道路场景图片的特征；本研究参考DNA所具有的能独特描述个体特征的特性，以序列的形式描述城市道路交通流时空特征，即道路交通流DNA特征。

由1.2.1可知，描述道路运行状态的特征共有9个，按照图3的顺序设置序列，以进行详尽描述。

图3所示特征序列以数据时间为序列头指针，对序列进行时间戳标记，后续序列窗格分别描述城市道路运行时的交通流各项特征；最后1个特征窗格标记中游路段交通流状态，以在匹配过程中标定待估计路段最终状态。则在匹配计算过程中各匹配因子分别用式（5）代表。

图3 城市道路交通流DNA序列Fig.3 DNA sequence of urban road traffic flow

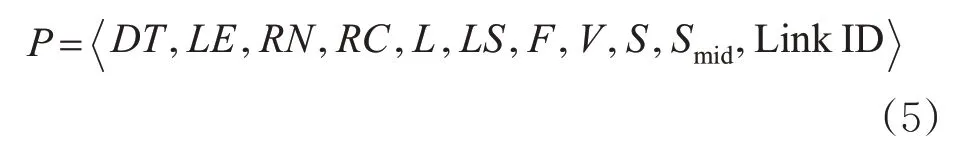
式（5）中，各符号与图3所示特征一一对应；另外，新增字段Link ID标记了该DNA序列产生的路段，以在GIS地图系统中进行路网拓扑搜索。数据时间作为时空特征序列头部、Link ID作为尾部，具有数据定位的作用；中游路段交通流状态作为匹配特征指标之一和结果集，具有双重作用；其他特征指标作为特征匹配的依据，称为“匹配因子集”，见图4。

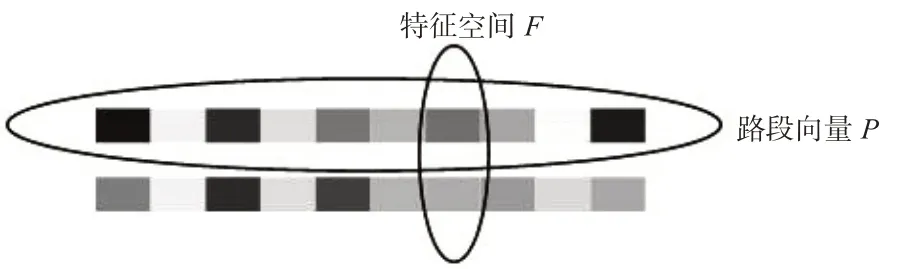
图4 路段向量与特征空间示意图Fig.4 Link vector and feature space

1.3 基于WH-KNN的城市交通流状态匹配

1.3.1 道路交通特征归一化

在城市道路交通网络中，各静态特征的可能性见表2。从表2中可以看出，道路交通流DNA静态特征序列的子结构特征可能性较少，然而组合可能性呈指数级增长；在匹配中静态与动态特征的结合，可能使得匹配数据集指数爆炸，不利于区分不同特征序列状态对匹配结果的影响。在匹配准确度不变的情况下，为提高匹配效率，将各特征数据进行归一化处理，以使得道路交通流DNA特征序列具有可比性。采用线性方法在[0,1]区间内完成归一化映射，各静态特征与动态特征取值、相应区间及归一化值见表3。

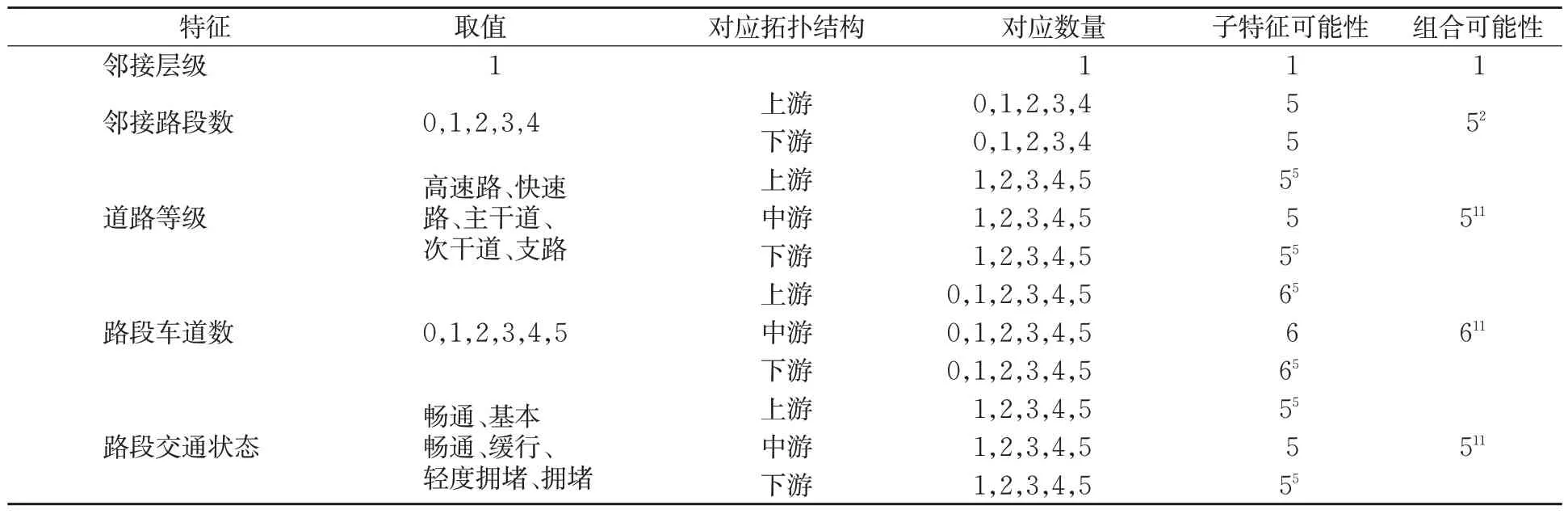
表2 特征结构及可能性数量表Tab.2 Feature structure and possibility

表3 时空特征归一化表Tab.3 Normalization of spatio-temporal features

在对应拓扑结构中，由于多个特征具有上、中、下游等多维度数据，因此采用矩阵的形式表示该特征值，矩阵的行对应拓扑结构，矩阵的列对应拓扑结构下的各特征的归一化值。为排除匹配过程中矩阵元素排序对匹配结果的影响，在数据存储过程中矩阵每行按照式（5）顺序存储；矩阵的列按照上-中-下游顺序进行列存储，每1个相同地理位置的拓扑结构（例如,同1个Link的每个邻接上游数据）按照Link编号大小的顺序排序。

1.3.2 道路交通特征匹配

城市道路时空特征序列匹配为时间粒度内的实时全路网匹配，以得到“距离最近”的路段交通流状态。针对图2中的每种特征，都需要构建1个特征匹配因子集，因此共需构建9个特征匹配因子集。在特征归一化的基础上，本文采用WH-KNN[22]进行特征匹配。在进行城市交通流状态匹配时常用到K近邻（K-Nearest Neighbor,KNN）方法[8，10]。WH-KNN（加权混合K近邻）方法通过引入权值来代替KNN算法中的类标签数目，有效解决2种算法的识别模糊性问题，提高匹配准确率。

采用WH-KNN对道路交通流DNA特征序列进行匹配时主要包括以下3个步骤。

步骤1。城市道路特征序列匹配因子集P F在KNN算法中采用欧氏距离计算各自的K F个近邻，见式（6）。

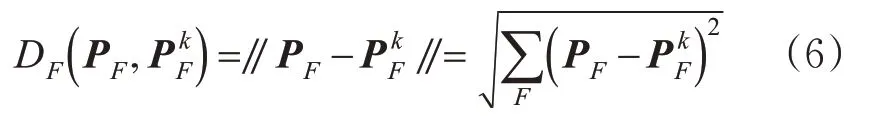
式中：下标F为式（5）中作欧氏距离运算的各特征因子集，构成各自的特征空间，在本研究中取前9个特征的匹配空间，取值[1，9]；P F和分别代表特征空间F中查询路段与第k个路段特征的归一化值，则表示查询路段与特征空间中第k个路段的欧氏距离。

步骤2。重复步骤1，直至所有道路时空特征因子集F中近邻特征的欧氏距离计算完毕。

步骤3。对每个道路时空特征因子集中的近邻赋予权值，其中最近邻权值最小，剩下近邻权值依次增大，见式（7）。

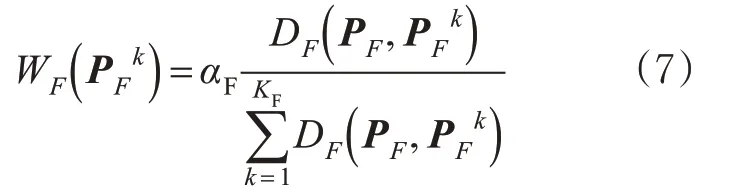
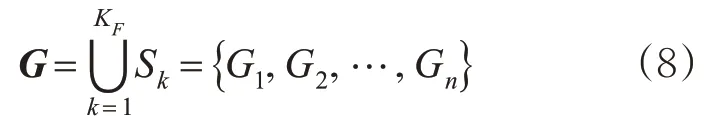
匹配目标就是在集合G中找到与查询路段“最近”的路段状态，即在集合G中找到权值最小的路段标签（“最近”意味着查询路段对应的道路交通流状态与数据库中某1个路段对应的状态最相似）。其中，每个路段标签G n对应的权值可用式（7）～（8）计算。

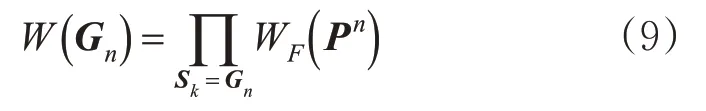
集合G包含了全部S k中的所有匹配结果，对于在多个特征空间计算得到的同1个近邻道路交通流状态，它为“最近”状态的概率更大，因此它的权值为各个特征空间分别计算得到的权值的乘积。最后，选择权值最小的近邻作为待估计道路交通流状态作为最近的状态，见式（10）。

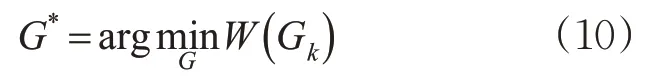
2 实验验证

实验数据来源于武汉市城市道路检测器数据，数据分为动态数据与静态数据。动态数据即随时间动态变化的道路交通流数据，由城市道路交通检测器检测得到，包括交通流量、速度、状态等。静态数据即道路参数和路网拓扑参数数据，包括道路等级、车道数等道路自身属性，以及邻接路段道路等级等拓扑属性。实验所用数据已经过清洗、多源融合等预处理。

2.1 城市道路交通流时空特性分析

为了进行城市道路交通流时空特性分析，选取武汉中环快速路编号为10483的Link路段，及其一级邻接上下游直行路段，路段编号分别为10468和8816。Link 10483为武汉市三环线金银湖路至常青路方向路段，全长3 326.4 m，共有3车道；Link 10468为Link 10483的上游直行路段，全长2 735.8 m，共有3车道；Link 8816为Link 10483的下游直行路段，全长2 087.1 m，共有4车道。

连续获取上述路段时间跨度为2020年10月23日—29日的卡口检测器交通流数据作为实验动态数据。数据时间粒度为5 min。由于卡口检测器检测到的速度数据为瞬时数据，不能反映车辆在路段上行驶时的整体状态，因此选择卡口检测器的流量数据进行处理分析。

2.1.1 时间特性分析

以Link 10483为例，时间粒度集成至1 h绘制1周流量趋势图，见图5。从图5可见：城市道路交通流数据呈现周期性的波动形式，其周期为1 d。交通流按时间序列发展变化，其数据呈现时间波动的特征，1 d交通流数据的波动趋势呈现按周期高峰期与平峰期交替重复的特性，即周期相似性；同时，工作日与非工作日具有不同的交通流变化趋势，典型区别见图5中星期一与星期日的流量-时间曲线。因此，笔者分别典型选取工作日（星期一）与非工作日（星期日）Link 10483的交通流数据作为交通流空间分析的基础数据。

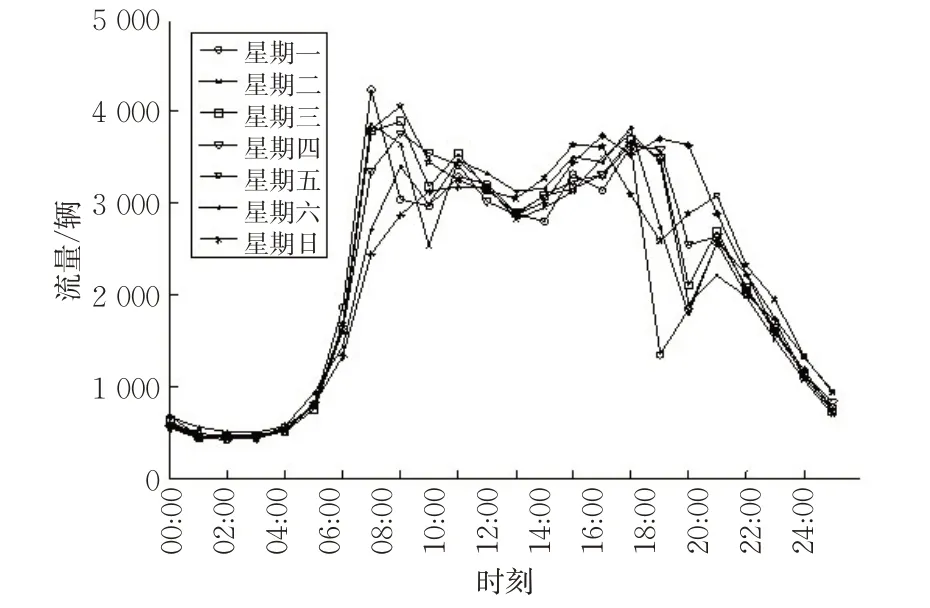
图5 Link 10483流量-时间曲线Fig.5 Flow-time curve of Link10483

2.1.2 空间特性分析

路段之间的连通性是城市道路拓扑网络基本特性之一。城市道路拓扑网络的连通性决定了交通流的流向，具有连通性的道路之间的交通流量变化是相互影响的。以Link 10483及其上下游直行路段工作日（星期一）与非工作日（星期日）的典型数据为例，上-中-下游路段之间1 d的流量变化关系见图6。图6（a）所示，在工作日中，17：00及之前时段Link 10483与上游Link 10468的流量在数值上较为详尽，且流量变化关系较为相关；而在17：00之后则与其下游Link 8816的流量变化较为相关；且其上午高峰时段流量与下午高峰时段流量相当。图6(b)所示在非工作日中，上-中-下游路段在1 d内的变化趋势较为一致，且下午高峰时段流量最大。

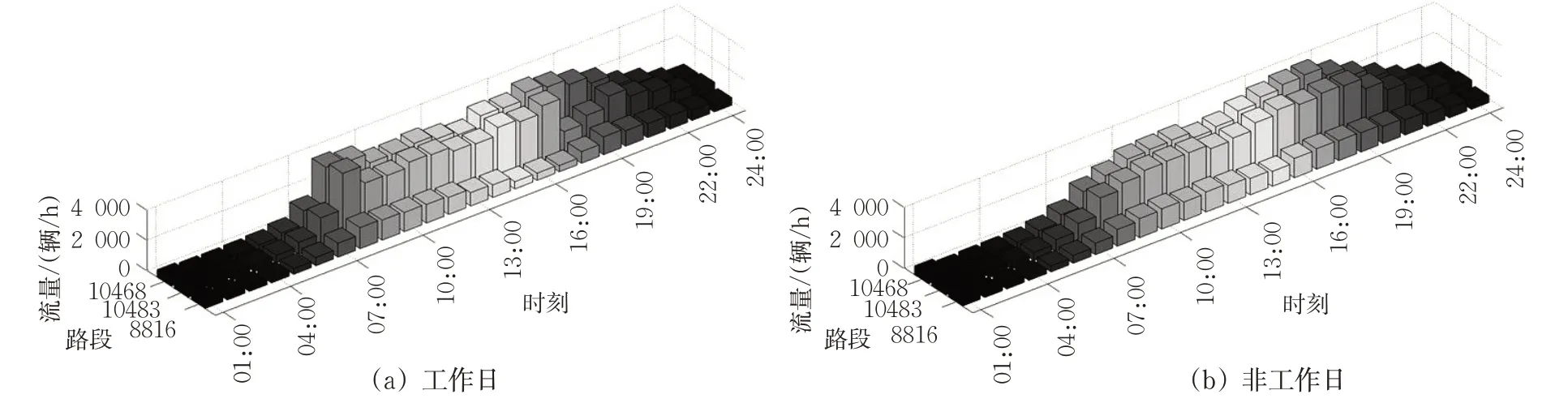
图6 Link 10483及其上下游直行路段典型流量关系Fig.6 Typical-flow relationship between Link10483 and its upstream and downstream straight sections

各个路段在同一时间粒度（描述路段内交通流参数的基本时间单位）内具有不同的流量值，然而将时间窗拉长至1 d后可发现上下游路段在1 d的时间内流量变化具有波动趋势相似性，即上下游路段交通参数变化具有相关性。因此，笔者将上下游道路参数与路网拓扑参数作为影响因素，考虑与待估计路段相连通的上下游路段交通流状态对待估计路段的影响。

2.2 城市道路交通流状态划分

1.1中通过计算行程时间比的方法，将交通流数据分为表1所示的5种交通状态:畅通、基本畅通、缓行、轻度拥堵、拥堵。采用1.1中所述方法对路网各个有数据的城市道路进行交通流状态划分，以建立预设的交通流状态数据库。

1.1中方法输入的基础数据为道路行程车速数据，见式（1）～（3）。本实验的速度数据为点速度数据，不符合速度的应用条件。同时，通过交通流参数的流密速关系可知，道路流量与道路行程车速之间具有相关关系，因此本节利用流量数据进行城市道路交通流状态预设。在此引入美国公路局BPR函数将路段流量转换为行程时间比。BPR函数见式（11）～（12）。

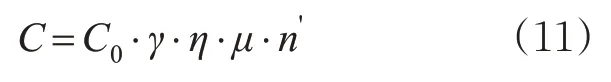
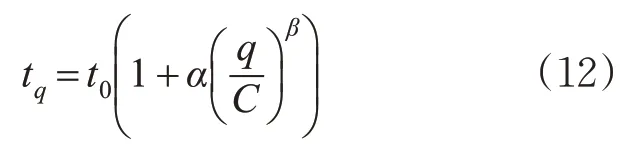
式中：t q为流量为q时路段的实际行程时间，s；t0为路段自由流行程时间，s；C为路段实际通行能力，pcu/h；α和β为回归系数，典型值为α=0.15，β=4；C0为理论通行能力，pcu/h；γ为非机动车影响修正系数；η为车道宽度影响修正系数；μ为交叉口影响修正系数；n'为车道数修正系数，车道数修正系数取值见表4。

表4 车道数修正系数取值表Tab.4 Correction factors of lane numbers

考虑到匹配特征序列包含“道路等级”这一特征，且路段实际通行能力C与道路等级密切相关，因此对于不同等级道路，设定不同的BPR函数参数[23]和道路通行能力值，见表5。

表5 BPR函数参数及道路通行能力值Tab.5 BPR function parameters and road-capacity values

运用上述所设参数进行城市交通流状态预设。以10483为例，预设其典型工作日与非工作日1 d内5 min时间粒度的交通流状态TPI10483。由式（1）～（3）计算后得到相应的TPI值，绘制交通流状态变化图，见图7。在图7中，0～1为“畅通”；1～2为“基本畅通”；2～3为“缓行”；3～4为“轻度拥堵”；4～5为“拥堵”。

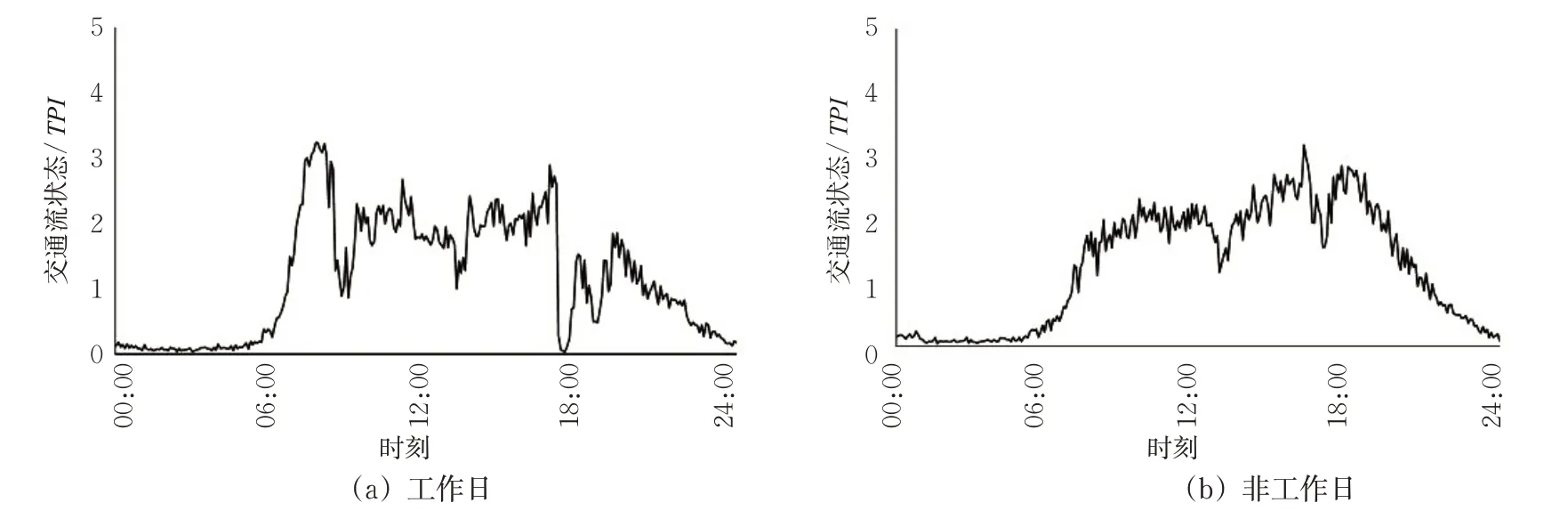
图7 Link 10483典型工作日与非工作日1 d交通流状态Fig.7 One-day traffic flow status in typical working day and non-working day of Link 10483

2.3 基于WH-KNN的交通状态数据匹配

WH-KNN在路网中的匹配示意图见图8。当路段检测器数据缺失时，中游路段状态栏数据为空，对应状态窗格无渲染；当算法根据各个特征值在数据库中搜索到最近的路段时，就能进行交通流状态渲染。图8中点画线为在临近时间粒度内找到了各特征空间内加权距离最近的路段状态；直线所示则为在当前时间粒度内匹配结果。

图8 路网交通流状态匹配示意图Fig.8 Matching of the road-network traffic-flow state

具体的WH-KNN数据匹配实验通过假定Link 10483数据缺失来进行。将路网中的路段构建成图3所示城市道路时空DNA特征序列，并表示成矩阵形式。Link 10483的特征序列为图3所示的流量（中游）、速度（中游）、交通流状态（中游）数据缺失的序列，即交通流参数缺失；利用可获得的3个参数，通过WH-KNN匹配得到Link 10483的交通流状态。刘国忠等[22]通过实验表明当近邻个数为2时，能够在保证准确率的情况下平衡特征提取时间与识别时间，因此本实验选取近邻个数k=2。最后将交通运行指数与表1匹配进行分级，判断查询结果的最近状态与Link 10483的原始状态是否一致，若一致则认为正确，否则错误，并计算实验时间段内运用该方法匹配得到的交通运行指数等级的正确率。

在WH-KNN交通状态匹配中，由于城市道路时空DNA特征序列被表示为矩阵的形式，因此每一特征空间匹配即为城市道路所有特征矩阵的匹配，即计算向量间的欧氏距离，匹配采用的各个特征归一化取值依据表3。

以武汉市卡口检测器1周检测数据作为实验数据，平均每天有数据约5 000万条；将每天数据按照检测器设备编号等信息匹配到Link上后，应用本文所述方法对Link 10483进行城市道路时空特征序列匹配，匹配的时间粒度为5 min。实验结果见图9。其中，虚线表示匹配结果，实线表示原始值。Link 10483的1周时空特征序列匹配结果，观察图9（a）～（g），平峰时段特征匹配的交通运行指数结果较为准确，状态估计在同1个等级的占90.9%；而高峰期存在一定程度的波动，但波动都在1个等级之内；对于交通流状态（交通运行等级）的描述，该方法匹配得到的结果具有一定的误差，但等级匹配准确率达到88%以上，且误判数据相差都在1个等级以内，在实际应用过程中不会给交通管理部门或者驾驶员造成较大的心理落差；星期一与星期五分别为工作日与非工作日的衔接点，在城市路网中都存在较大的车流，路网中路段上车流的不确定性较大，其匹配准确率较低，除此之外1周内其他天的匹配结果则保持在90%及以上。实验验证了本文所提方法的可行性。

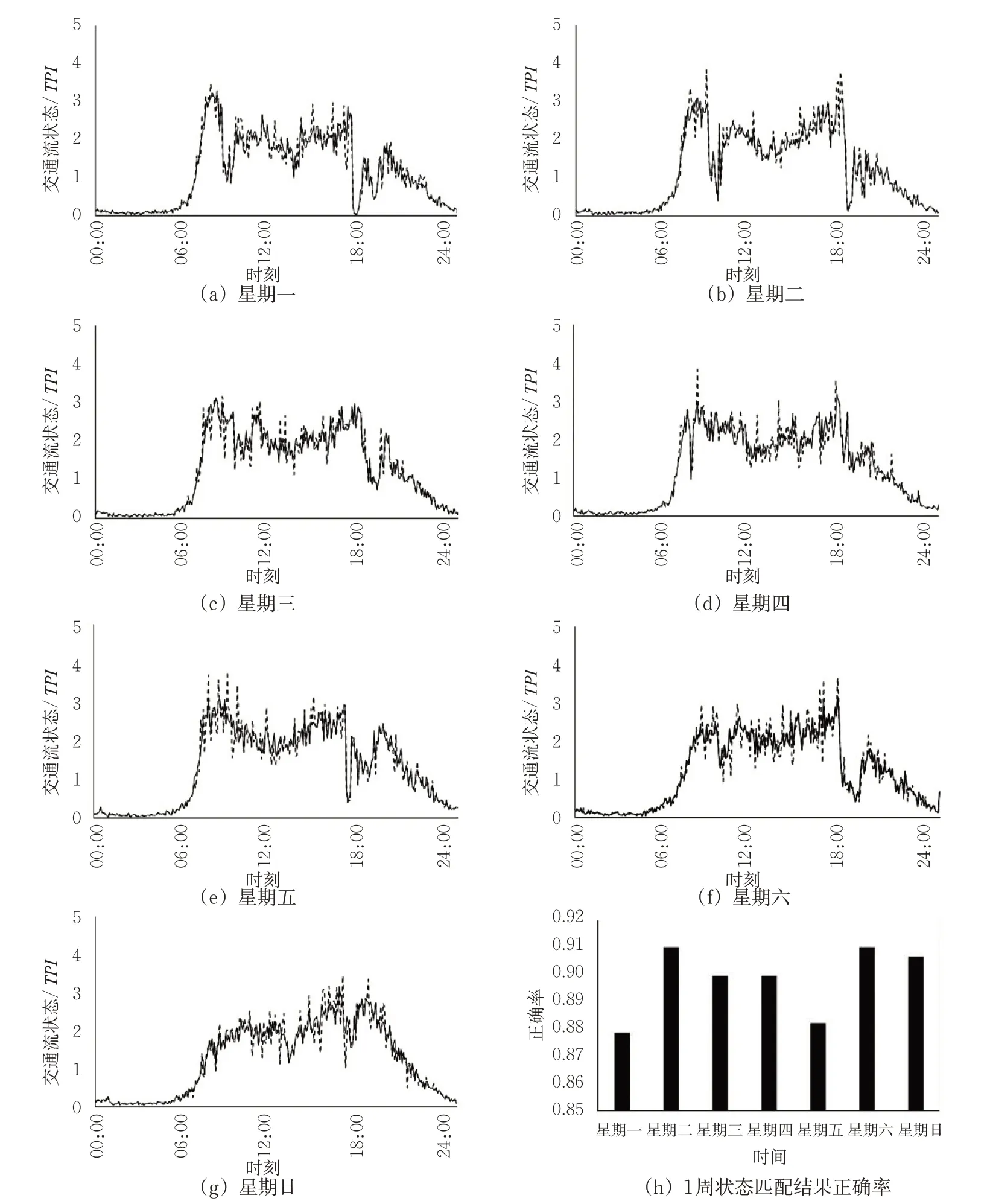
图9 Link 10483的1周匹配结果与正确率对比Fig.9 Comparison of one-week matching result and correct rates of Link 10483

3 结束语

文中通过分析城市道路网络中交通流的影响因素与运行规律，构建了1种基于时空特征序列的城市交通流状态估计模型。首先通过已有的城市道路交通运行指数计算方法预设路网中有动态交通参数数据路段的交通流状态；然后分析城市道路交通流状态的影响因素，提取了3个维度、8个特征、1个附加维度的描述城市道路交通流状态的特征序列，并将其编码为道路交通状态DNA序列，同时转换为定量的匹配因子；最后路网中路段的特征进行归一化处理，并利用WH-KNN的方法对无动态交通参数的路段进行状态匹配。结果表明，该城市道路时空特征序列匹配模型不仅能够得到没有检测器数据路段的交通流状态，提高城市道路网络的智能管控范围，且其性能良好，交通状态的判别率较高，误判的严重程度较低。在进一步研究中，将使用其他道路等级的交通数据验证和分析模型性能。