多目标公交车辆与司机调度问题元启发算法设计*

孔云峰

（河南大学黄河中下游地理信息技术教育部重点实验室 河南 开封475000）

0 引 言

我国城市公共交通事业近年发展快速。①城市道路、公交专道、停车场、充电设施、公交站台等基础设施不断完善；②运营公交车辆数量保持增长，车辆性能和舒适度得到明显提升，且环保清洁的电动车辆占比越来越高；③公交信息化日益普及，大多数公交企业已建成信息化平台，提供车辆与司机管理、车辆跟踪、收银结算、客户服务等，部分城市建成目标更高的智慧公交系统。整体上，城市公交服务水平得到明显提升。

公交线网优化是公交企业提升服务水平和生产效率的关键，也是智慧公交系统的核心功能。A.Ceder等[1]将公交线网优化划分为5个过程：公交网络设计、发车频率设置、时刻表确定、车辆调度和司机排班等过程。K.Kepaptsoglou等[2]详细地归纳了公交线网设计问题的模型定义、主要特征和求解方法。针对发达国家公交企业车辆与司机调度问题，R.Pine等[3]完成的专题报告及后续更新报告[4]提供了1套解决方案，基本步骤如下：①车辆调度（blocking）：根据公交班次任务进行车辆调度，最小化车辆数量及行驶成本，形成若干班次链（block）；②司机调度（runcutting）：划分班次链为若干任务段，分段点作为潜在的司机交接班时间和地点；根据司机工作时间、休息、就餐、报酬制度等，为司机分派任务，目标是降低所需司机数量和薪酬成本；③司机轮班（rostering）：根据司机休假时间规定，按月安排司机轮班工作和休息。其中，司机调度问题最为困难，原因在于任务段组合空间巨大，且司机工作规范及薪酬规定企业间差异很大。通常采用“生成与选择”方法求解司机调度问题：生成是根据调度经验生成数以十万计的班次链，选择是求解1个覆盖集问题模型，从候选班次链中选择1个成本较低的方案。除了使用遗传算法求解覆盖集问题，学者也提出了其他优化方法，如基于禁忌搜索与遗传算法的混合元启发算法［5］、贪婪随机自适应搜索（GRASP）算法［6］、列生成算法［7］等。另外，C.Valouxis等[8]提出使用混合算法进行车辆与司机一体化调度。

我国学者也开展了多样化的研究。针对公交车辆调度问题，魏明等［9］针对跨线车辆调度问题，以车辆数量、车辆等待和空驶时间最少为目标，考虑车场容量、车辆加油等因素，设计了蚁群算法，并使用5条线路上238个公交班次对算法进行了验证；李一凡等［10］构建了多车场多车型公交车调度问题的线性规划模型，使用Gurobi优化器求解，并讨论了电动车辆使用成本的变化对公交运营总成本的影响；姚恩建等［11］针对电动车辆跨线调度问题，设计遗传算法进行求解，并以北京市大兴区4条公交线路进行算法验证；滕靖等［12］采用粒子群算法求解单条线路上纯电动公交车辆运营时刻表设计和车辆调度问题，在上海市的1条公交线路验证了算法的可用性；唐春艳等［13］设计遗传算法求解电动公交车辆调度问题，在灵活调整发车时间的前提下减少所需车辆数量，提升车辆利用率。

针对司机调度问题，刘涛［14］系统地研究了公交司机排班问题的模型，比较了3种算法的求解性能；陈明明等［15］以最小化乘务组成本、停留等待成本和空驶成本为目标，采用禁忌搜索算法优化多车场公交乘务排班问题；陈程［16］探讨了兼顾车辆和司机的多目标公交车辆调度优化算法，力图找到Pareto最优集；陈明明［17］针对多种公交管理模式系统地讨论了相关的问题模型和算法；侯彦娥等［18］针对人车固定管理模式，提出混合元启发算法求解车辆调度与司机排班问题，通过13个案例测试验证了算法的有效性。

国内外学者长期关注城市公交线网优化与运营管理，但针对我国城市公交管理模式的算法研究仍充满挑战：①我国公交企业通常采用单条线路且人车固定的运营管理模式，导致国际上按车辆调度、司机排班和司机轮班顺序进行作业规划的方法难以直接使用；②面向国内公交企业的车辆调度与司机排班问题研究存在若干局限，如问题定义过于简化导致算法适用性差，车辆调度未考虑司机排班，算法功能单一，测试案例偏少且案例规模偏小等，难以为公交企业提供1套较为完整的解决方案。基于此，笔者设计了1个混合元启发算法，用于求解多个公交车辆与司机调度问题，支持燃油车辆或电动车辆、单线或跨线、人车国定或人车分离模式的调度模式。使用62个单线案例和11个跨线案例，从多个角度测试算法的功能和性能，力图为公交企业提供1个功能齐全、性能优良、灵活通用的生产作业计划编制工具。

1 问题定义

令集合R={r1，r2，…，rm}、V={v1，v2，…，v n}、D={d1，d2，…，d p}和S={s1，s2，…，s q}分别表示m条公交线路、n个班次任务、p个停车场q个公交线路起讫点。每条公交线路上具有若干班次的公交任务，任务vi具有以下属性：线路编号、起点站、终点站、起始时间和结束时间。令t ij表示车辆从站点i空驶到站点j的时间（i，j∈D∪S）。

令班次链B k={d k，v k1，v k2，…，v ku，d k}，表示公交车辆k从车场d k（d k∈D）出发，依次完成u个公交任务，最终回到出发车场。当司机固定驾驶某1辆车（人车固定）时，可按司机工作要求为B k配置1～2名司机。当允许司机换驾车辆（人车分离）时，先进行车辆调度，再进行司机调度。车辆运行线路和司机驾驶任务均使用班次链表达。

班次链B k的可行性定义如下：①针对车辆行驶，2个连续任务之间的时间间隔需大于某1个预先给定的数值，如前1个任务运行时间的百分比10%。该值设置较大时，车辆在公交线路起讫点的等待时间偏长，可能导致需要较多的车辆；反之，需要较少的车辆，但当某1辆车出现晚点时，将影响后续班次任务的执行，也会导致司机休息时间得不到保证；②当车辆为电动车辆时，假设车辆在夜间完成充电，在运行过程中，可能需要在合适的时间和地点进行快速充电；③针对司机调度，班次链B k需考虑司机休息和就餐，例如，司机连续驾驶超过4 h，必须休息0.5 h以上；在规定的就餐时间段内，必须有0.5 h以上的就餐时间。

定义如下班次链参数：2个相邻班次的时间间隔为前1个任务时间的某一百分比gap，是车辆到站后执行下1个任务的等待时间，用于司机休息或交接班；司机连续驾驶超过t ltmin必须休息至少t lbmin；司机在11∶00—13∶00和17∶00—20∶00之间必须提供至少t mmin就餐时间；针对电动车辆，给定电池有效电量G，kW·h、平均每分钟耗电g1，kW·h、每分钟可充电g2，kW·h，用于判断电池是否需要充电、是否能够充电及充电时长。基于这些参数判断班次链的可行性。

与班次链B k相关的成本如下：①车辆固定成本cbf，包括车辆的年折旧成本、维护费用和保险费用；②车辆运行成本f1(B k)，包括行驶成本、空驶惩罚成本、充电成本等。给定班次链B k，车辆行驶时间、空驶时间、充电时间和时长均已知，可通过定义单位成本计算运行成本：车辆每分钟行驶成本cbd、车辆空驶每分钟惩罚成本c be、电池充电1次折旧成本c ec及浮动电价c0，c1，…，c23（代表0时，1时，…，23时的电价）；③司机固定成本f2(B k)。为班次链B k分派司机，一般有4种可能：1名正常班司机、1名高峰班司机、1名长班司机或2名正常班司机。考虑司机轮班作业，该班次链B k所需司机数量分别约为1.4，1.5，2.0和2.8。定义司机固定成本为c df，4种司机配置方式的司机固定成本分别为1.4c df，1.5cdf，2.0cdf和2.8cdf；④司机津贴成本f3(B k)，如加班津贴、异地收工津贴、换车惩罚等。企业对于司机的津贴政策可能差异很大，根据实际需要计算司机津贴成本。

基于以上成本定义，构造多成本目标函数。对于“人车固定”问题，采用班次链集合B={B1，B2，…，B K}表示该案例的1个解。其目标函数为：f(B)=∑b∈B(cbf+f1(b)+f2(b)+f3(b))。对于“人车分离”问题，先求解车辆行驶班次链B'，再求解司机班次链B''，其目标函数分别为f(B')=∑b∈B'(cbf+f1(b))和f(B'')=∑b∈B''(f2(b)+f3(b))。若班次链不满足约束条件，赋予其足够大的成本，阻止非可行班次链的出现。

根据实际需要，定义司机工作班制：正常班、高峰班和长班。①正常班司机驾驶车辆时间小于t dn1且上下班时间间隔小于t dn2，如分别取值为7.5，10 h；②高峰班司机驾驶车辆时间小于t dp1，上下班时间间隔小于t dp2，且高峰间休息时间大于t dp3，如三者取值分别为7.5，13，3 h；③长班司机驾驶车辆时间小于t dl1，且上下班时间间隔小于t dl2，如分别取值为10.5，13 h。

2 算法设计

笔者基于迭代局部搜索（ILS）设计了1个混合元启发算法求解车辆调度与司机排班问题。ILS算法从1个初始解开始，迭代地进行扰动和局部搜索。局部搜索能够不断地改进当前解，但容易陷入局部最优；对当前解的扰动能够使算法脱离局部最优，进而提升搜索性能。为进一步提升ILS算法性能，对其进行2个方面的扩展：群解搜索和变邻域下降（VND）搜索。给定参数群大小（psize）和连续未更新最好解循环数（mloops），算法流程步骤见图1。

与基于单解的邻域搜索算法相比，本文算法维护1组精英解。首先，算法步骤1生成1组初始解；其次，在每1次迭代搜索中，从群解中随机选择1个解进行搜索（步骤2）进行扰动（步骤3）和搜索（步骤4）；再次，搜索完成后，使用新解更新群解（步骤5）。群解更新时，优先考虑解的目标值，其次考虑解的差异程度，保持解之间有一定的差异。维护1组具有差异度的精英解，能够扩大解空间搜索范围，有利于改进求解质量。最后，由步骤6判断连续未更新最好解循环次数是否达到阈值（mloops），若是则算法终止，否则继续搜索。

ILS中使用VND搜索能够使每轮搜索达到局部最优。VND方法反复使用邻域搜索算子进行搜索，直到所有算子均不能提升当前解，获得局部最优解。ILS中频繁使用扰动方法，若当前解不是局部最优，下轮搜索中很容易被破坏，减少了到达局部最优的机会。因此，VND搜索用于ILS算法，有利于提成算法求解质量。

算法中，步骤1使用车辆调度问题（VSP）模型产生初始解。车辆调度要求：所有任务必须被执行、车辆在任务间等待时间满足参数Gap要求；调度目标是车辆固定成本和运行成本最低。实验表明，商用CPLEX优化器（https：//www.ibm.com/analytics/cplex-optimizer）或开源CBC优化器（https：//coin-or.Github.io/cbc/）均能够高效地求解VSP模型。对于人车分离模式，VSP模型求解结果即可用于车辆调度。此时，车辆班次链通常不满足司机休息和就餐时间规定，可将其分拆，直到满足要求为止。分拆后的班次链集合作为后续问题的初始解。

班次链操作采用4种方式［18］：①单班次移动，即将1个班次链中的某个班次删除，插入到另1个班次链中；②双班次移动，即将1个班次链中2个相邻的班次删除，插入到另外1个班次链中；③班次链交叉，即将2个班次链分别从某个位置截断，然后再将断开的班次链进行交叉组合；④班次链合并，即将2个班次链合并生成1个新的班次链。以上操作用于步骤4的搜索改进，其中，班次链交叉用于步骤3的扰动操作。

针对不同的调度模式，采用不同的成本目标函数。人车分离模式，分别使用司机固定成本和司机津贴成本。而人车固定模式，使用车辆和司机总成本。

基于以上算法原理，笔者实现了1个通用算法，满足单条线路或多条线路、燃油车辆或电动车辆、人车固定或人车分离等情形下的问题求解。基本模块如下。

1）基础数据管理模块。管理公交车场、线路、首尾车站、班次任务时刻表、站点/站场间距离和空驶时间等基础信息。

2）问题定义模块。使用配置文件，设置问题类型和参数。问题类型包括：燃油车辆人车固定作业、电动车辆人车固定作业、燃油车辆人车分离作业和电动车辆人车分离作业。问题参数较多，包括车辆相关成本、司机相关成本、司机班制定义、司机休息及就餐时间规定等。

3）班次链评价模块。将问题解表达为班次链集合，针对每个班次链，进行可行性判断操作，包括班次间隔时间可行性判断，电动车辆是否需要充电判断，电动车辆需要充电时是否有合适的地点和时段进行充电，司机就餐可行性判断，司机休息可行性判断等。第二类操作包括各类成本的计算，重点是根据班次链匹配最优司机班制，按成本顺序依次判断该班次链是否满足1名正常班司机、1名高峰班司机、1名长班司机或2名正常班司机。

4）初始解构造。依据车辆运行时间间隔设置要求，构造车辆调度问题模型，求解模型获得若干车辆班次链。若某个班次链不满足司机休息及就餐要求，将该班次链分拆，直到班次链具有可行性。

5）班次链搜索算子。包括单班次移动、双班次移动、班次链交叉、班次链合并、班次链拆分等班次链调整算子，循环调用算子改进车辆调度和司机排班方案。

6）参数设置模块。提供算法参数，如解群规模、计算时间限制、目标值未改进的连续循环次数等。

3 案例测试

3.1 案例数据及作业参数设置

笔者收集了62条公交线路数据对本文算法进行测试。数据来源于3个大型城市H、G和Z，多是城市干线公交线路，均为双向发车；线路长度处于8.9～60.4 km之间，平均26.1 km；线路班次行驶时间处于25.8～145.3 min，平均83.0 min，详细情况见表1。表1中，单程时间为所有班次的平均运行时间。大部分案例中，线路起点和终点均设置停车场；个别案例中，停车场与线路起点或终点间需要5～10 min的行驶时间。

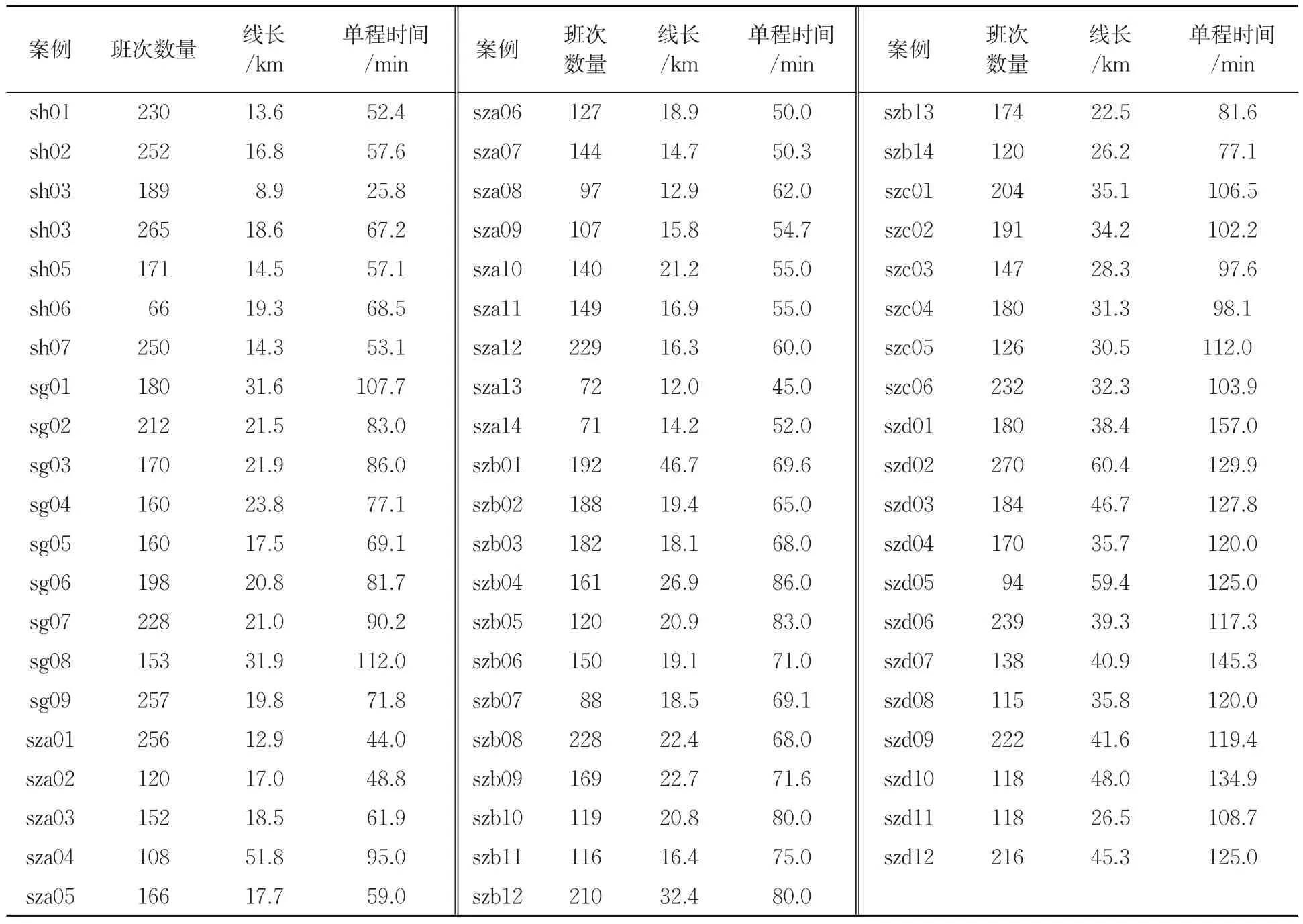
表1 单线案例基本特征Tab.1 Main features of the single-route instances

为测试跨线作业，设计了11条跨线案例，见表2。设计方法如下：在1个城市选择2～4条公交线路，假定其上行方向的起点站相同，作为枢纽站点进行跨线调度。

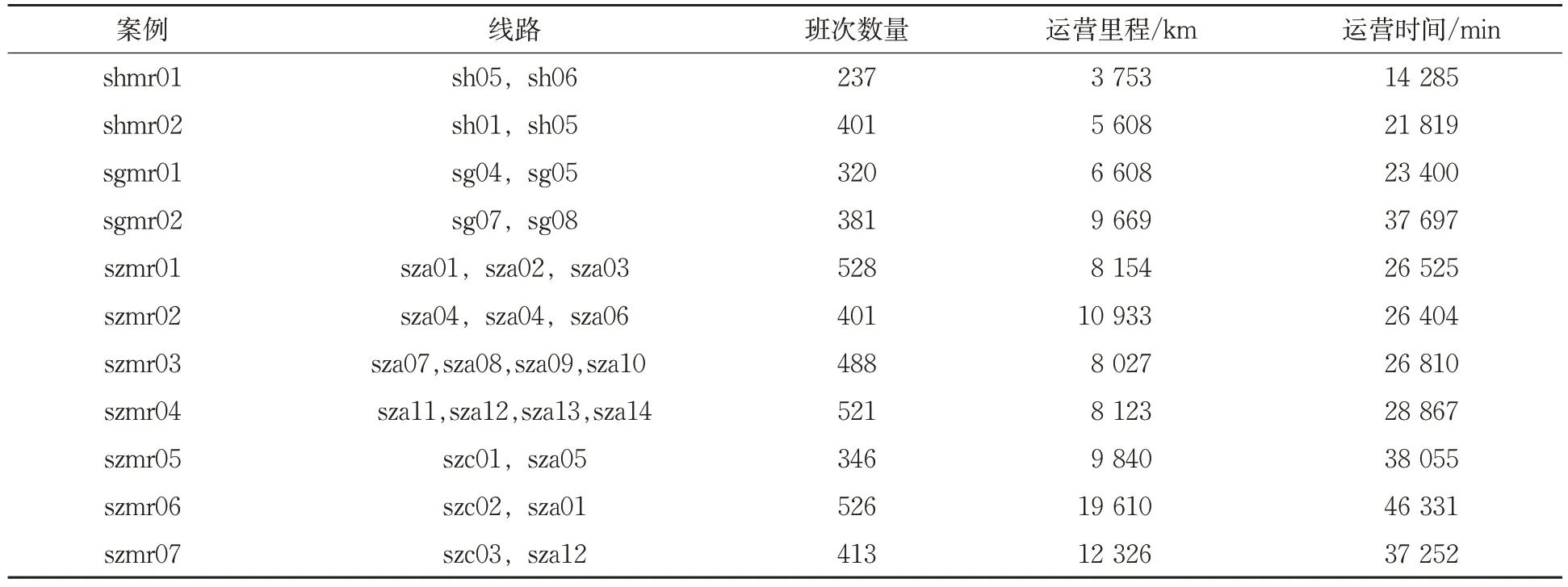
表2 跨线案例基本特征Tab.2 Main features of the multi-route instances

使用以上案例，进行车辆与司机调度实验。每个案例数据对应4个问题类型：①燃油车辆人车固定作业；②电动车辆人车固定作业；③燃油车辆人车分离作业；④电动车辆人车分离作业。针对电动车辆，选择2种车型，电池有效容量分别为150，120 kW·h。应当注意，电动汽车耗电情况较为复杂，将充电、耗电模型简化为线性函数，未考虑地形、车辆载重、行驶速度变化、环境温度、电池衰减等因素。实际应用中，应根据电池理论性能和作业监测数据建立更精细的能耗模型。

实验设计的主要参数如下：车辆固定成本cbf=200 000元，车辆每分钟行驶成本cbd=1元，车辆空驶每分钟惩罚成本cbe=1 000元；电动车辆电池有效电量G=150或120 kW·h、行驶平均每分钟耗电g1=0.3 kW·h、每分钟可充电g2=2.0 kW·h；电池1次充电折旧成本cec=30，浮动电价c0，c1，…，c23处于0.5～1.0元之间。司机固定成本c df=100 000元；司机班制规定如下：正常班t dn1=7.5 h，t dn2=10 h；高峰班tdp1=7.5 h，tdp2=14 h和tdp3=3 h；长班tdl1=10.5 h和tdl2=13 h；司机休息规定参数tlt=4 h和tlb=0.5 h，就餐时间t m=0.5 h。车辆或司机班次链中，2个连续任务的停车间隔不小于前1个任务时长的10%，即gap=10%。另外，要求车辆完成班次任务后，必须回到出发地。

本文算法使用Python语言编程实现，测试环境为PC机，配置Core i7-6 700 3.40GHz CPU、8G内存、Windows10 64位操作系统。VSP模型采用CPLEX 12.6优化器求解。为加快算法执行速度，在PyPy（https：//www.pypy.org）环境中运行算法。

3.2 单线调度结果

针对62条单线案例，进行车辆与司机调度。每个案例设置调度场景如下：采用燃油车辆、配置150 kWh电池的电动车辆（“电动1”）和配置120 kWh电池的电动车辆（“电动2”），并分别按人车固定和人车分离模式进行调度。这样，每个案例获得6个调度结果，调度结果满足前节设置的参数约束。因数据量较大，表3按案例分组列出主要指标，即每组案例所需车辆数量、单日所需司机数量、轮班所需司机数量及车辆空驶次数。根据司机数量和班制估算轮班司机数量，按照前述定义，司机数量出现了小数。

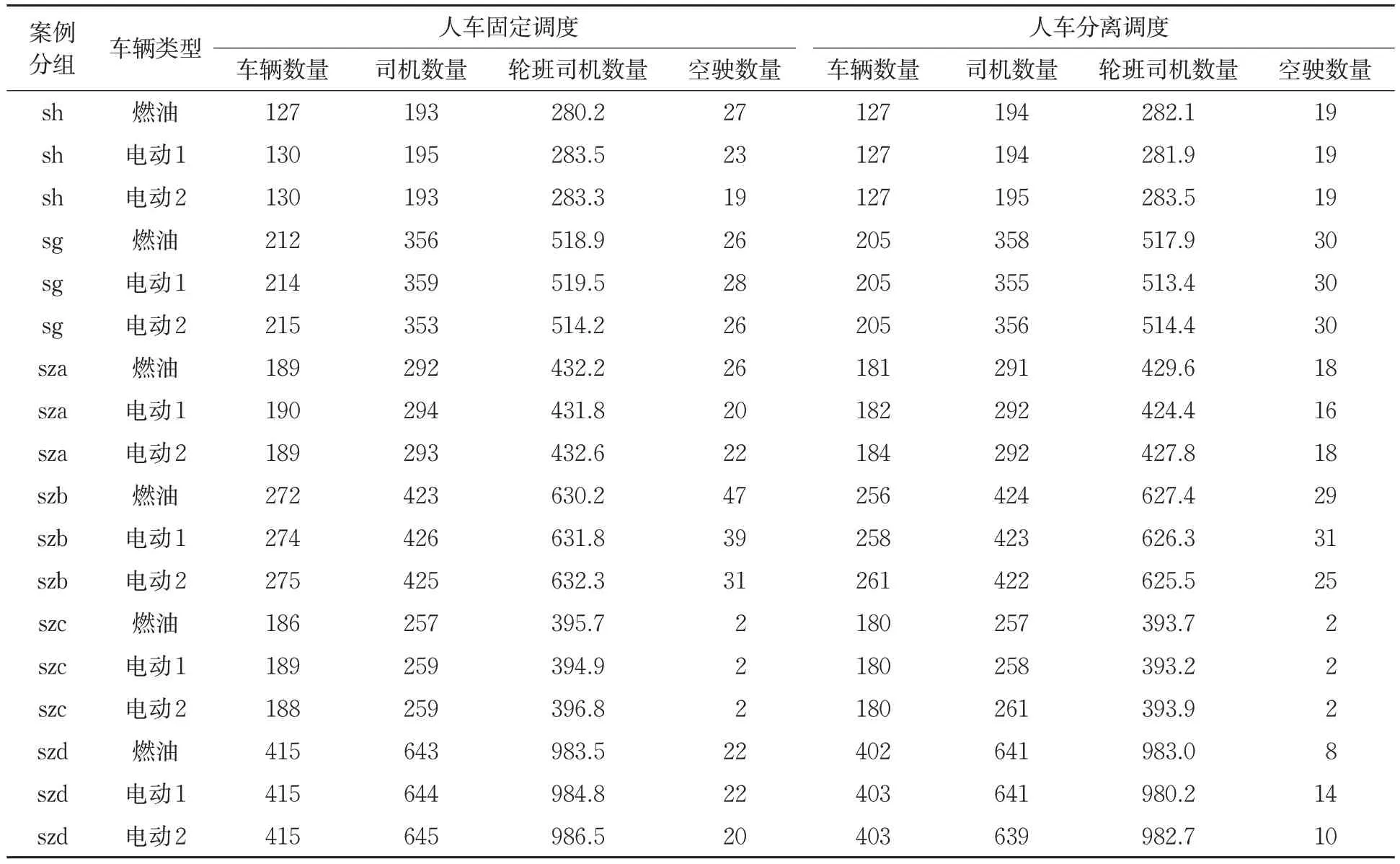
表3 单条线路作业计划统计Tab.3 Scheduling results from the single-route instances

比较调度模式可以发现：①使用电动车辆取代燃油车辆，人车固定模式下，大多数线路无需增加车辆，个别线路需增加1辆车，平均增加0.8%；而人车分离模式，平均增加0.3%较高性能车辆或0.7%较低性能车辆；所需司机数量，总体上无明显变化；②与人车固定调度模式相比，人车分离调度能够减少所需车辆3.8%，减少司机0.4%，减少空驶次数20.3%，但司机在1个工作日内需要换车约2次；③针对燃油车辆人车固定模式，车辆日均行驶10.3 h,行程189.6 km，司机日均驾车6.7 h,行程123.6 km，表明车辆利用率较高，司机工作时间安排合理。

3.3 跨线调度结果

针对11个跨线案例进行车辆与司机调度。每个案例设置调度场景如下：采用燃油车辆或电动车辆，并分别按人车固定和人车分离模式进行调度。表4为全部案例4种调度场景的主要结果，包括所需车辆数量、所需司机数量和车辆空驶次数，并与单线调度结果进行比较。结果比较发现：①与单线调度相比，跨线调度减少车辆4.6%，减少司机2.4%，但平均增加1.5次空驶；同时，每车日均运营由201 km提升到211 km，司机日均驾车服务里程由123 km提升到126 km；②使用电动车辆取代燃油车辆，人车固定模式需增加0～2辆车，平均增加1.6%，而人车分离不需增加车辆；③与人车固定调度模式相比，人车分离减少车辆2.6%，司机数量保持基本不变，空驶减少7.9%，但每个司机在1个工作日内需要换车约2次。总体上，因长短线路相协调，车辆调度更加灵活，能显著地减少所需车辆；同样，司机工作时间更为均衡，且容易为司机安排合理的休息和就餐时间。跨线调度使调度规模大幅度增加，作业计划编者更为困难，手工作业难以胜任，必须依靠性能良好的调度算法工具。

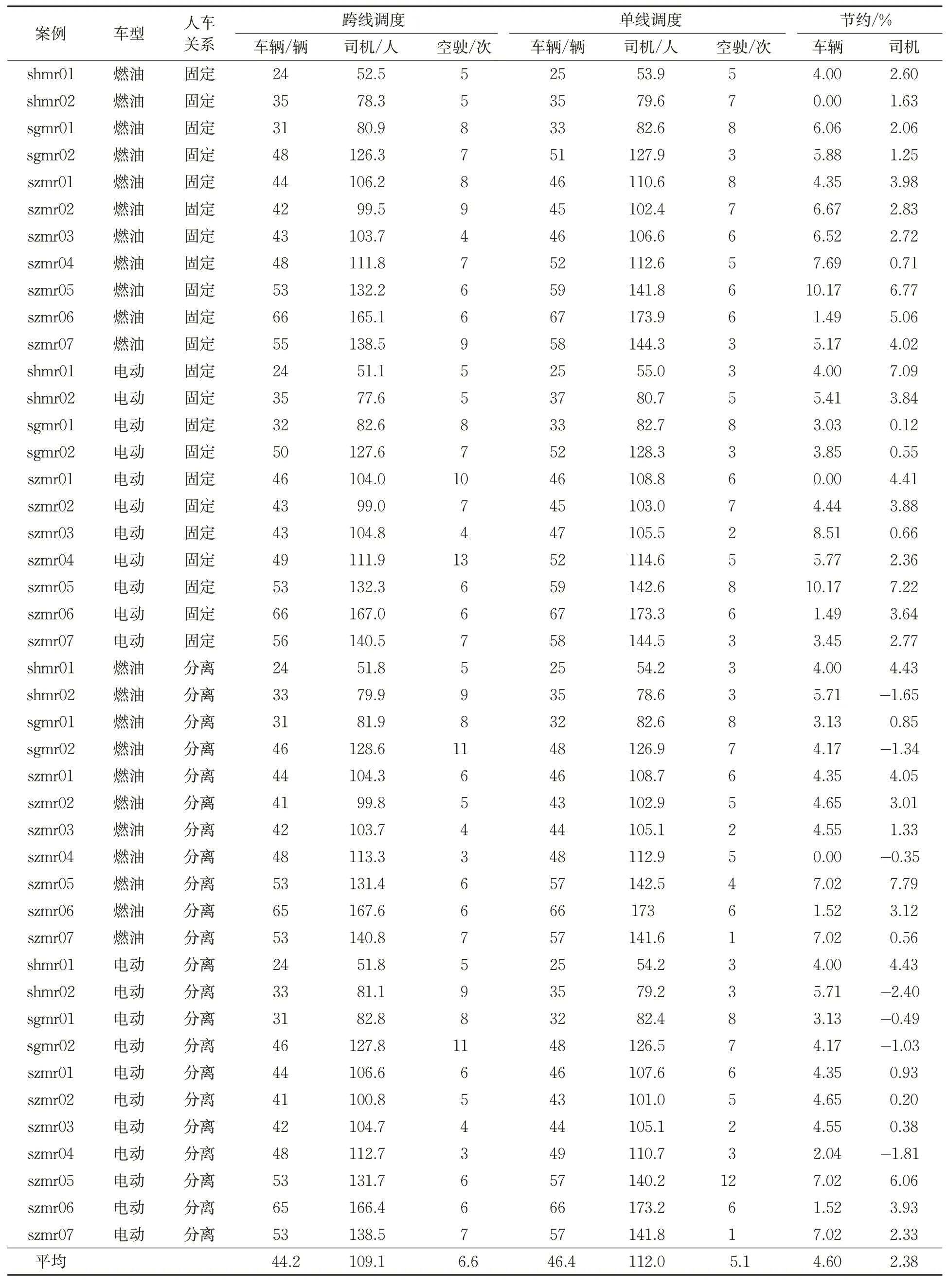
表4 跨线调度结果及与单线调度比较Tab.4 Scheduling results from the multi-route instances

3.4 参数分析

本文实现的算法不仅满足多模式公交车辆与司机调度，而且支持公交运营参数的设置。为验证参数设置对调度结果的影响，选择3个单线案例和1个跨线案例进行测试。表5是改变车辆中停时间参数gap的计算结果，其他参数与前节案例测试相同，调度模式为燃油车辆人车固定。表中，车辆、司机和空驶分别表示所需车辆辆数、所需司机个数和车辆空驶次数。可以看出：随gap增加，所需车辆数量增加，增加幅度显著；随gap增加，单日公交作业所需司机数量、空驶数量有一定的波动。

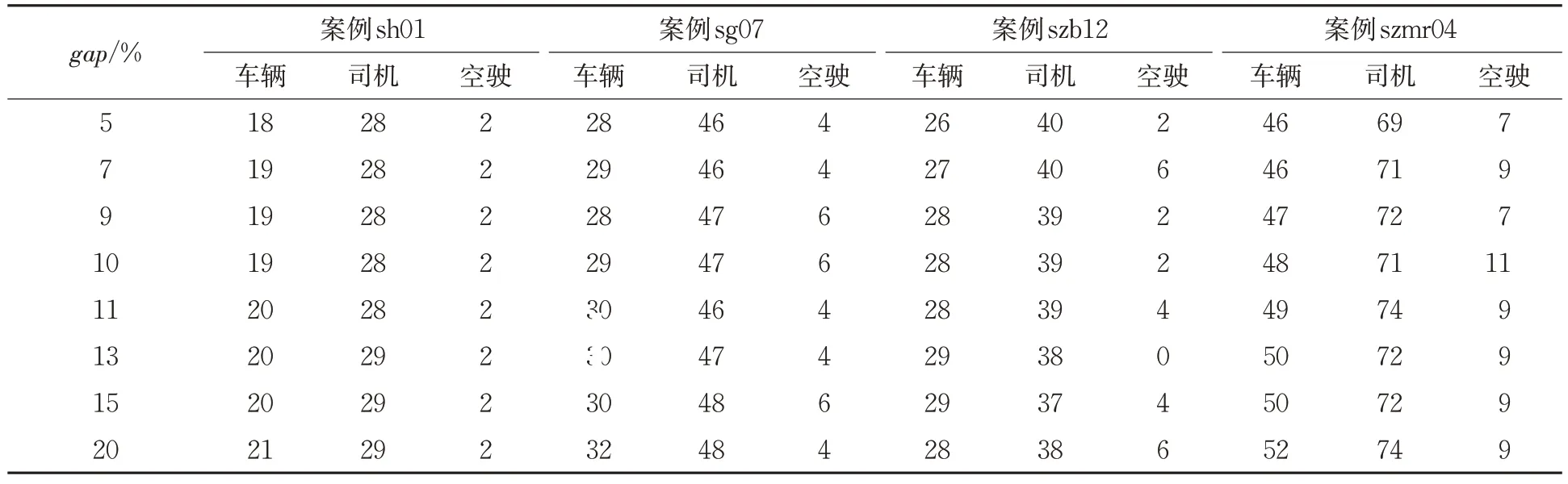
表5 车辆中停时间（gap）对车辆调度的影响Tab.5 Effects of the waiting time(gap)for buses on scheduling results

进一步测试司机班制设计对车辆与司机调度的影响。针对4个案例，设计5种班制，除司机班制定义外，其他参数与前节案例测试相同，调度模式为燃油车辆人车固定。计算结果见表6。可以看出：所需车辆与司机数量受司机班制影响较大，但对于不同的案例，其影响差异较大。针对案例sh01，因其双峰特征突出，不允许高峰班会使所需司机数量大幅增加；而对于案例sg07，szb12和szmr04，不允许长班会使所需司机数量大幅增加。对于案例szb12，因单班次任务时间为80 m，正常班时间为7.5 h或长班时间限制在10.5 h，难以提高司机的工作效率。综上，司机工作班制设计对于公交司机调度影响显著。一方面需要高峰班和长班减少所需司机数量；另一方面，需要根据线路特征适当修改工作时长参数，有利于合理地为司机分派任务。

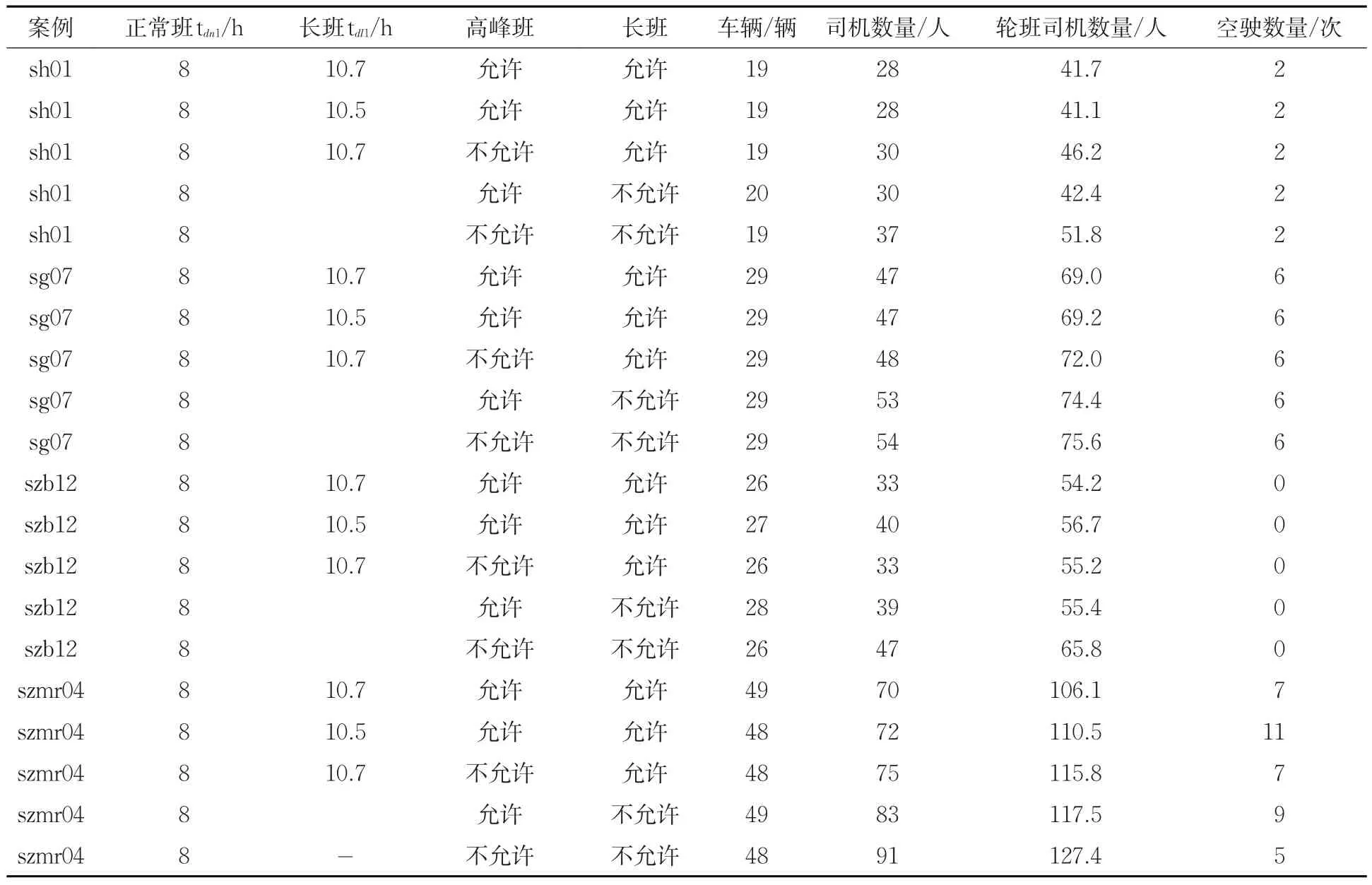
表6 司机班制设计对公交作业的影响Tab.6 Effects of the design of drivers'working shifts on scheduling results

3.5 计算时间

本文案例测试时间统计见表7。表7中给出了6个单线调度案例组中每个案例的平均计算时间，11个跨线调度案例的计算时间。可以看出，计算时间与案例规模相关，也受线路长度、服务时长、所需车辆和司机数量的影响。对于相同的案例数据，使用电动车辆比使用燃油车辆计算时间大幅增加，因需要检测电池续航能力，并设置充电时间和地点。对于跨线调度案例，计算时间大幅增加，因部分搜索算子计算复杂度为O（n2），随案例规模增大，所需计算时间大幅增加。考虑到公交作业计划编制不是日常性工作，本文算法计算时间可以接受。

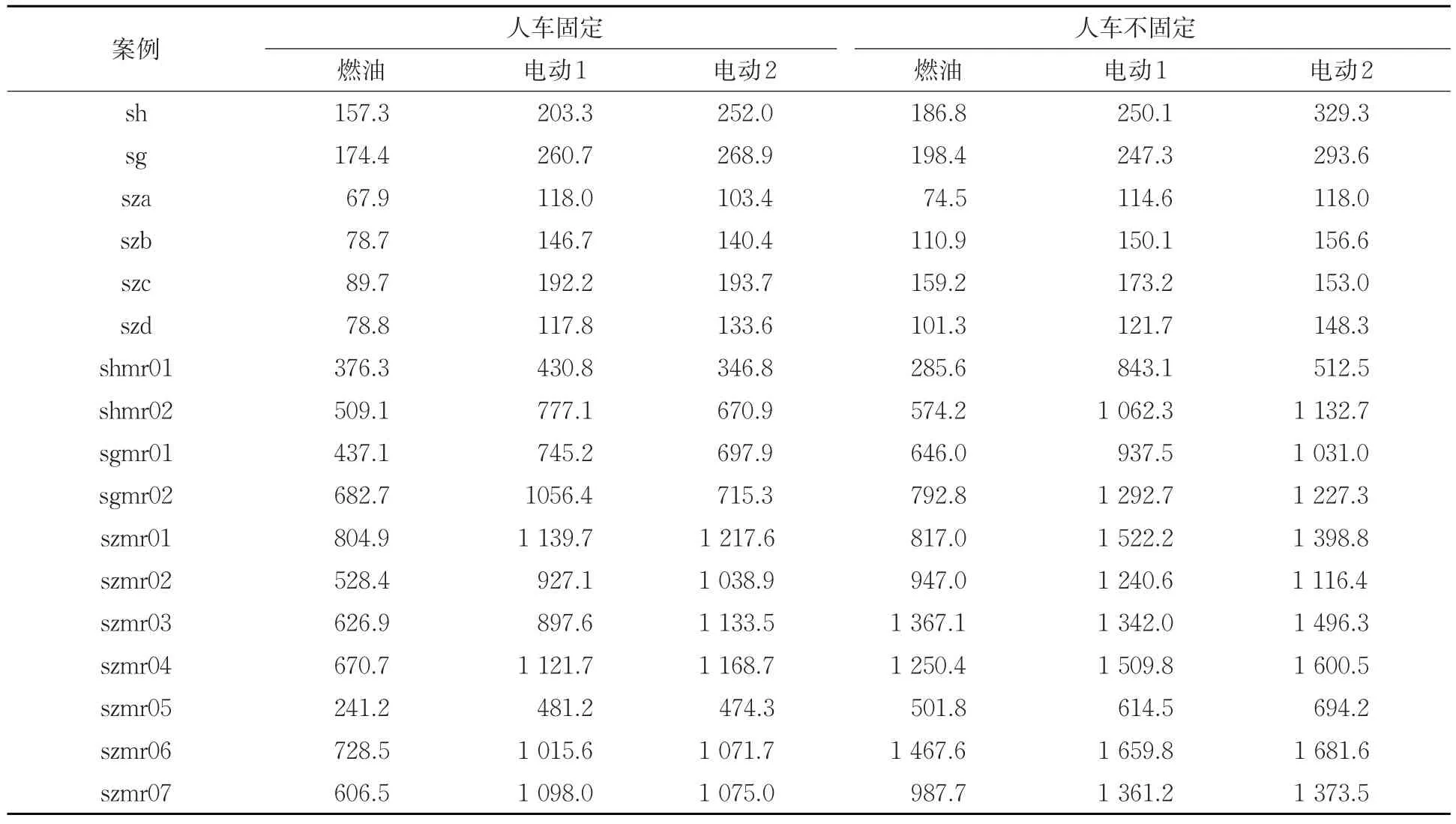
表7 案例计算时间Tab.7 Statistics of computing times on cases s

4 结束语

笔者设计了1个公交车辆与司机调度问题的元启发算法。算法顾及车辆停车时间、电池充电、司机休息与就餐等约束条件，优化目标包括车辆固定成本、车辆行驶成本、司机固定成本和司机津贴成本。算法首先生成初始解、再迭代使用班次链算子改进当前解，并通过群解、扰动和可变邻域下降等策略改进解的质量。算法支持燃油车辆或电动车辆调度，适用于单线或跨线运营管理，满足人车固定或人车分离模式的作业计划编制，也支持灵活的问题参数设置和算法参数设置，具有良好的通用性。

本文使用62个单线案例和11个跨线案例进行算法测试，并比较了不同运营模式下生产作业方案的差异。测试结果验证了算法的功能和性能，单线案例平均计算时间为163 s，跨线案例平均为936 s，运行时间可以接受。针对车辆与司机调度模式比较发现：案例中大多数公交线路能够以1∶1的比例使用电动车辆取代燃油车辆；部分公交线路采用跨线运营后，车辆和司机效率提高显著；车辆执行任务间隔时间设置对于车辆利用率影响显著；工作班制设计对于公交司机调度影响显著，多班制组合及根据线路特征设置班制参数，有利于提升司机工作效率；与人车固定模式相比，人车分离运营能提升车辆和司机的效率，但司机日均2次的换车作业增加了管理难度。

与国际公交车辆与司机调度算法相比，本文算法支持人车固定调度模式，满足国内公交企业的现实需求。与国内研究相比，本文算法具有明显的优势：充分考虑车辆和司机相关的成本；支持多种调度模式，具有通用性；案例测试充分，特别是测试了大规模跨线调度案例，验证了算法的性能。另外，案例测试结果对于国内公交企业运营决策具有借鉴价值。

本文提出的公交车辆与司机调度问题的通用算法尚需进一步发展：①针对人车分离模式，司机换车次数偏多，因此有必要在算法中增加司机换车次数约束及相关的搜索策略；②算法的计算效率有待进一步提高，特别是针对跨线调度运营模式；③本文算法应当在应用中进一步发展和改进。