基于模糊突变的水利工程脆弱性评价探讨

朱远东，欧正蜂

(1.广东省水利水电科学研究院，广东 广州 510635；2.广东省水动力学应用研究重点实验室，广东 广州 510635；3.河口水利技术国家地方联合工程实验室，广东 广州 510635)

近年来，我国出现大范围极端温度、强降水和强台风等极端性天气，导致水利工程系统的不确定性日益凸显，次生自然灾害频发，使得水利工程系统风险和脆弱性不断增加。由于水利工程系统具有多层次多维度的特性，各子系统联系密切，高度耦合，特别是当突发、极端事件发生时，其运行过程受内、外部因素的胁迫和扰动更为剧烈，系统的稳定性能将大幅降低。若胁迫和扰动作用突破了系统自我恢复极限，则会造成严重的后果，甚至引发系统崩溃。由于传统线性模型难以实现对水利工程脆弱性的激发因素及其复杂的不确定突发过程进行解析，而Rene·Thom所创立的突变理论在处理非线性的突发性事件问题表现出色，因此被广泛的应用于工程领域。

有关脆弱性的研究起源于20世纪80年代对致灾因子论的反思[1]。1975年，White拓展了防灾减灾研究范畴，率先对人类面对洪灾时的脆弱性进行了研究[2]。当前有关水利学科的脆弱性研究主要集中在水资源、水环境领域，而对于水利工程的脆弱性研究则涉及很少。如黄木易[3]等基于网格单元尺度对1970—2015年间巢湖流域水环境保护区景观生态脆弱性进行分析研究；张永芳[4]、任源鑫[5]、杜娟娟[6]等通过构建多维度的脆弱性评价指标体系，采用AHP—熵权、综合指数评估、综合赋权等方法，分别对河北、陕西和山西省水资源的脆弱性予以评价。因此，本文基于突变理论，引入模糊数学，建立模糊突变模型并对水利工程的脆弱性进行研究分析和量化评价，可为水利工程的风险评价提供参考。

1 基本理论

1.1 突变理论

突变理论是由法国数学家雷勒·托姆(ReneThom)于1972年创立的，以突破学、奇点理论为数学工具，对基于未知系统的内部作用的研究尤为适用，可较好地解决不连续问题，为研究自然界中突变现象的数学桥梁和纽带。突变理论中以控制变量和状态变量来描述系统，其中系统突变原因的连续变化因素称为控制变量，而系统的行为状态用状态变量表示。一般意义上的突变理论，实际指的是由Thom根据空间中分歧集的几何形态所总结出的7种初等突变模型，即抛物形、椭圆形、双曲形、蝴蝶形、燕尾形、尖角形和折线形。

在工程实际中，尖点、燕尾和蝴蝶型突变模型应用比较广泛，目前已被引入到灾害系统研究[7-8]，脆弱性分析评价[9-10]，工程安全评价[11-12]、风险评价[13-14]以及稳定性分析[15-17]等实际工程问题和理论研究中，取得了较好的应用效果。

1.2 模糊聚类分析法

模糊聚类分析数据数理统计中多元分析的一种，是按照特定标准来鉴别事物间的接近程度，并将性质接近的事物进行归类的数学方法[18]。由于客观事物之间并没有明确的界限，为模糊数学理论的诞生及其引入聚类分析提供了理论基础。

2 模糊突变评价指标体系构建

当突发性事件发生时，水利工程的脆弱性极其容易被激发，究其原因，主要来源于水利工程自身因素和外在因素的共同作用。因此，充分挖掘和分析水利工程脆弱性触发的驱动因子，建立符合水利工程特性的脆弱性评价指标体系，对水利工程的风险评价分析具有重要的意义。

2.1 评价指标选取

由于水利工程在运行过程中同时受到内外界活动的干扰作用，其脆弱程度与系统承受的破坏和恢复活动具有直接相关性。当恢复活动程度可以制约破坏活动的发展时，水利工程则处于稳定状态；反之，水利工程则向溃决的方向演化。当影响系统稳定性的破坏活动无法制约时，系统的脆弱性会被极大地激发并发生突跳，导致系统从安全状态跳跃到崩溃状态，由此水利工程的稳定性被破坏，将导致水灾害事件发生。

综合考虑水利工程系统的复杂性和影响因素的多层次性，本文将整个系统逐级细分成由多个指标组成的多层系统，将激发水利工程系统脆弱性的控制变量分为3个层次。原生脆弱性包括突发事件指数(E)、工程地质状况(G)、水文气象条件(H)以及自然地理环境概况(N)4个方面影响因素，包含4项定性指标和9项定量指标；水利工程外在脆弱性主要来源于技术(T)、管理(M)、社会(S)以及人员(P)脆弱性4个层面，包含13项定性指标。

依据突变理论原理，通过指标重要性程度排序，按照底层指标数量，选用尖点突变(J)、燕尾突变(Y)和蝴蝶突变模型(H)等不同突变模型，按照归一公式逐层向上量化递归运算，求得最高层评价指标突变级数值，对照评判集进行脆弱性评价(评价指标体系见图1)。

图1 水利工程脆弱性评价指标体系示意

2.2 评价指标处理

在指标评价过程中，通常是定性和定量指标并存，因此通常采用定性与定量相结合的方法得到相关底层指标的初始值。对于模糊、不确定性的定性指标，参照文献[19]通过采用专家打分法和模糊综合评价相结合的方法进行规格化处理。定量指标采用极差变换法进行无量纲化处理。对于正向指标，按式(1)进行转换，逆向指标则按式(2)进行转换，从而将原始数据转化为[0，1]区间上的越大越优型指标值。

(1)

(2)

为使模型中的各变量指标的性质和量纲统一，控制变量的数值分别作放大和缩小处理，则可将其取值制满足条件的模糊隶属函数取值区间内，由此可推出常见初等突变模型的归一公式见表1所示。

表1 常见突变模型的归一公式

2.3 确定隶属函数值

水利工程脆弱性评价指标众多，部分指标可能密切关联，甚至可以相互替代，因此，在对水利工程脆弱性进行模糊突变综合评价时，要充分考虑指标间的关联性。当各控制指标间具有明显相关性，则适用“互补”原则，即以控制变量对应的突变隶属函数的平均值作为系统的x值；反之，适用“非互补”原则，取最小值。在计算过程中，根据底层指标数量分别选用尖点突变、燕尾突变和蝴蝶突变模型相对应的归一公式，由指标底层逐层向上进行量化递归运算，最终求得最高层评价指标突变级数值，并依据评判集进行脆弱性评价。

2.4 确立评判集

根据水利工程脆弱性评价实际情况，将水利工程评价指标的评判等级划分为4类：不脆弱、低度、中度和脆弱。各评判等级评级值区间根据底层指标赋值逐步向上层递归推算求得，当底层所有指标评价值为Yij=1时，则最高层综合评价值V=1，表示水利工程不存在任何脆弱性；反之当Yij=0，表示水利工程系统已经崩溃。

参考已有研究成果[20-22]，按照可靠度和水利工程设计规范，结合水利工程实际，各底层指标分别取0.6、0.8和0.9作为水利工程高、中、低度脆弱和不脆弱的临界值，并由底层指标逐步向上层递归求得最高层综合评价值V分别为：V=0.89、V=0.95和V=0.98，则相应评判值区间见表2。

表2 水利工程脆弱性评判等级区间

3 工程案例分析

3.1 工程概况

某中型水库位于澜沧江水系南碧河上游，坝址海拔为1 100.0 m，距当地县城6 km，交通便利，以农田灌溉、工业供水为主，兼顾防洪。水库径流面积为47 km2，年均径流量为482.4万m3，总库容为1 236.8万m3，正常蓄水位为1 098.60 m，设计洪水位为1 099.04 m，校核洪水位为1 099.21 m，工程等别为三等，主、次要建筑物级别分别为3级和4级；设计洪水标准为50年一遇(P=2%)，校核洪水标准为千年一遇(P=0.1%)。

该水库枢纽工程包括主、副坝、输水隧洞和溢洪道。水库设有管理所，负责水库运行调度管理，机构健全，管理规范，现有管理人员17人，负责水库工程的日常运行管理工作。在全省水库的安全评价中，综合评定该水库大坝安全等级为三类坝。其中，该水库工程质量为不合格；运行管理等级为较好；防洪安全复核评价属于A级；大坝抗滑稳定安全系数存在小于现行规范值，抗滑稳定性差，综合评价等级为C级；现状水位情况下，出逸水力坡降均大于允许水力坡降，易于发生渗透变形(流土)破坏，综合评价渗流安全等级为C级；大坝抗震稳定安全系数均小于现行规范值，综合评价等级为C级；输泄水建筑物评价为B级；金属结构安全评价等级为B级。

3.2 底层基础指标评价值确定

根据该水库相关设计资料和安全评估专家报告，以及相关机构对水库大坝的质量检测和土工试验报告，对上述25项评价指标按照定量指标通过计算予以确定，定性指标通过专家打分予以量化的原则，采用定性与定量相结合的方法进行量化，获得各底层指标的百分制初始值，对其标准化处理后获得结果见表3。

表3 水利工程脆弱性底层指标标准化处理

3.3 归一化计算

3.3.1原生脆弱性突变分析

根据上文分析原生脆弱性影响因素集可描述为Y={E,G,H,N}，其中E表示突发事件脆弱性，G表示工程地质脆弱性，H表示水文气象条件脆弱性，N表示自然地理脆弱性。

一级影响因素集：E={E1,E2,E3,E4}，G={G1,G2}，H={H1,H2}，N={N1,N2,N3}

水利工程原生脆弱性的4个控制变量E、G、H和N适用于非互补型的蝴蝶突变模型，其中E1、E2、E3、E4构成互补型蝴蝶突变模型，G1、G2和H1、H2分别构成尖点突变模型，N1、N2和N3适用燕尾突变模型。根据归一公式，逐级向上层递归运算求得各变量的突变级数值为：xE=0.57，xG=0.98，xH=0.94，xN=0.99，由于指标不具有显著相互关联性，故适用非互补原则，取最小值，从而得到水利工程原生脆弱性总突变隶属函数值x(Y)=0.57，相关评判指标及归一化计算结果见表4所示。

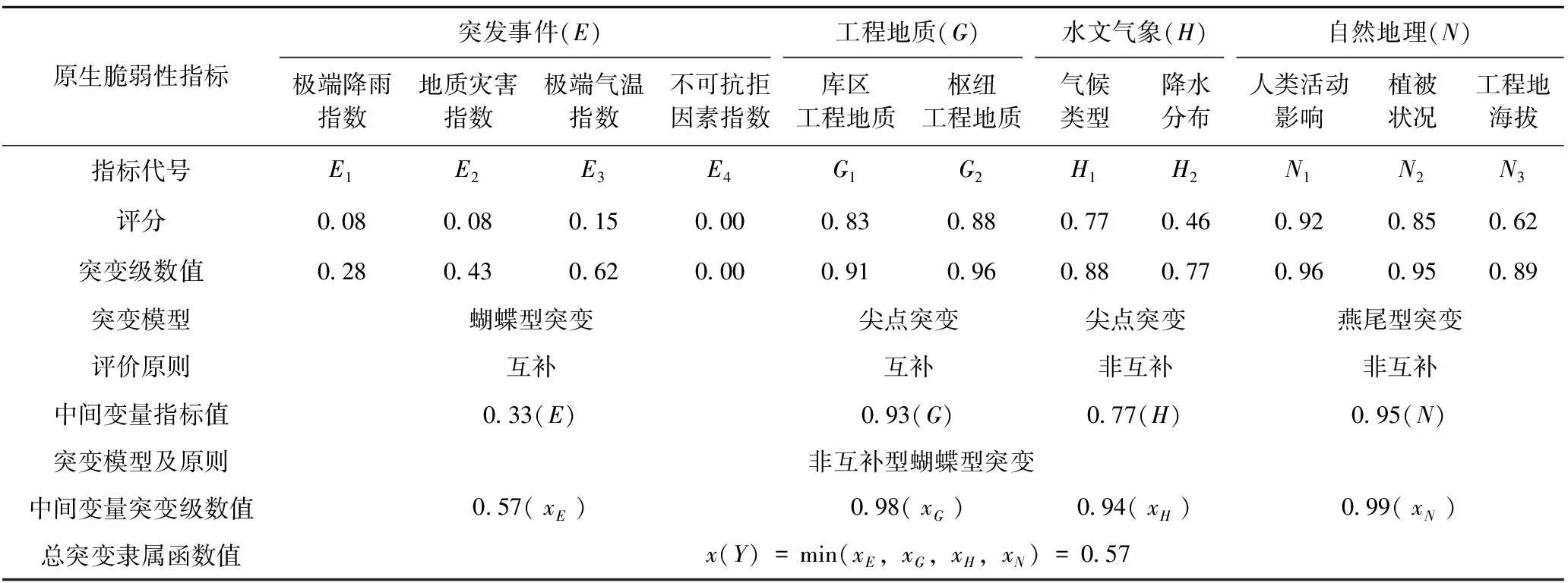
表4 水利工程原生脆弱性评判指标及归一化计算果

3.3.2水利工程外在脆弱性分析

水利工程外在脆弱性可描述为W={T,M,P,S}，其中T表示技术脆弱性，M表示管理脆弱性，P表示人员脆弱性，S表示社会脆弱性。分别对技术、管理、人员和社会脆弱性的突变过程进行分析计算，得到突变级数值分别为：xT=0.94、xM=0.99、xP=0.98和xS=0.96，根据相应评价原则求得控制变量W的突变隶属函数值为x(W)=0.94。

3.3.3水利工程脆弱性突变分析

基于上述计算过程，求得水利工程原生脆弱性和外在脆弱性的总突变隶属函数值分别x(Y)=0.57和x(W)=0.94。由于水利工程脆弱性是水利工程原生脆弱源和外在脆弱源共同作用的结果，故而以Y和W控制变量构建尖点突变模型，求得其相应的突变级数值分别为：xY=0.75、xW=0.98。由于Y和W之间作用结果具有可替代性，因此适用互补原则，取平均值，故水利工程脆弱性的总突变隶属函数值为x(V)=0.88。相关因素评判指标及归一化计算结果见表5。

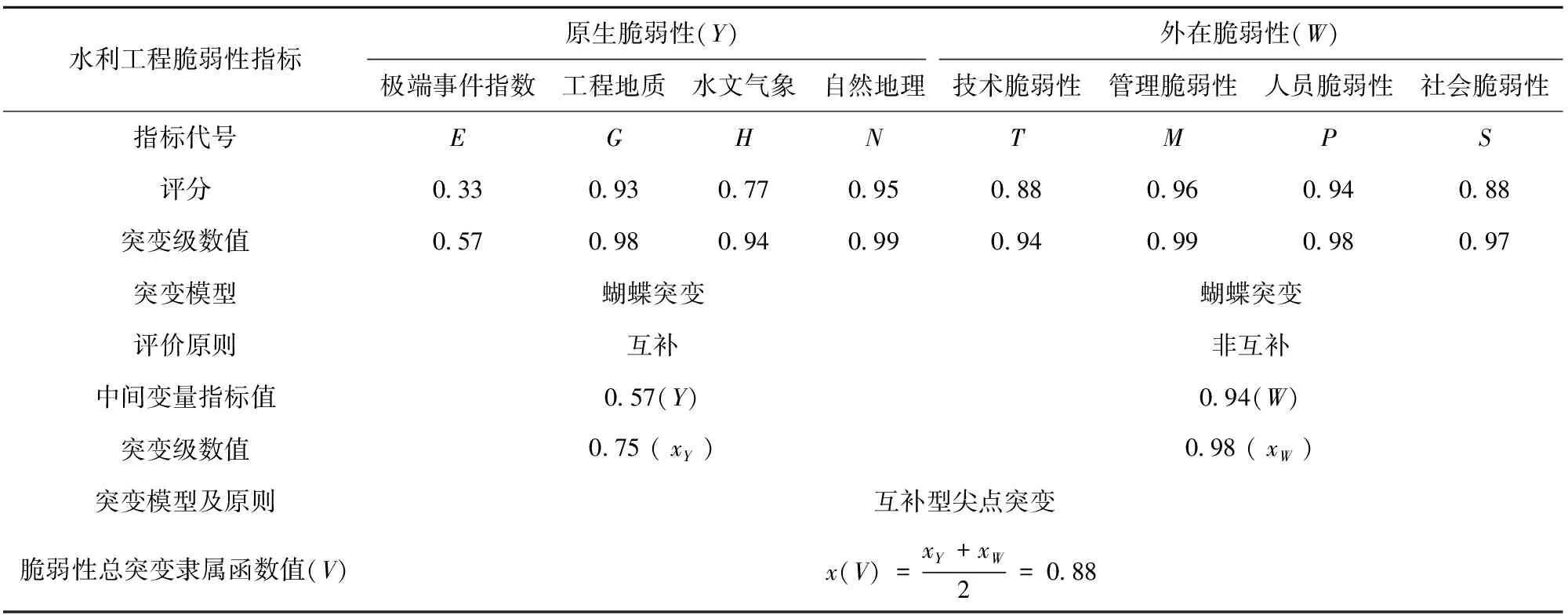
表5 水利工程脆弱性评判指标及归一化计算

3.4 评价结果分析

根据计算结果，将利工程脆弱性一二级影响指标及其突变级数值列于表6。

1)对照表2所列水利工程脆弱性等级划分标准可知，该水利工程属于高度脆弱等级，与上级水利部门出具的安全鉴定评价结果相吻合，证明该评价方法可靠。

2)表6数据显示，该水利工程原生脆弱性明显高于外在脆弱性，主要在于考虑了极端事件的影响。在极端气候环境下，原生脆弱性的破坏作用较外在脆弱性具有更大的破坏力。水利工程原生脆弱性影响因素中自然地理属于低度脆弱，工程地质状况属于中度脆弱，水文气象条件属于高度脆弱，基本符合安全鉴定专家报告相关内容。

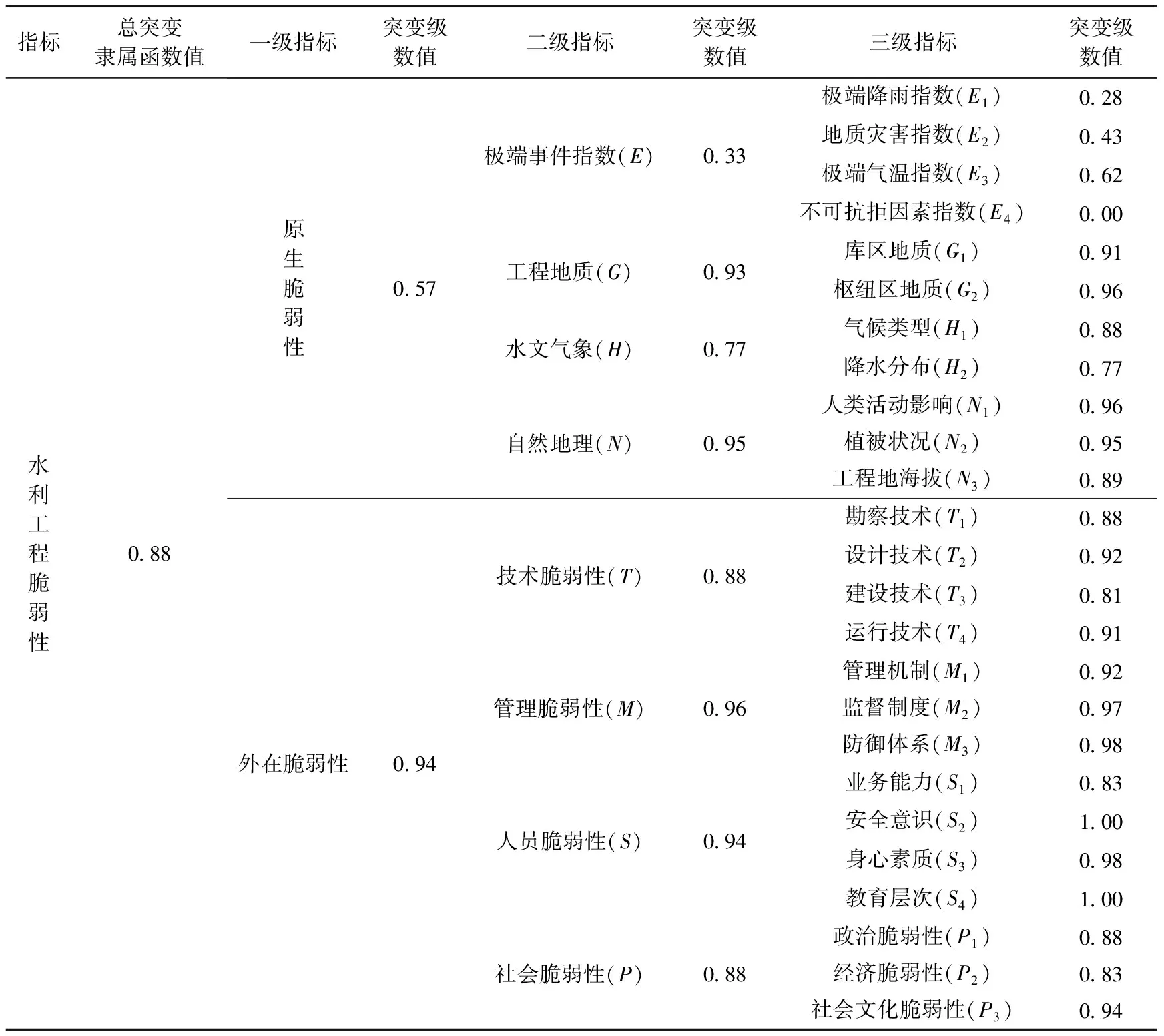
表6 水利工程脆弱性突变评价结果分析

3)表6数据显示，该水利工程技术脆弱性为高度脆弱，其下级指标勘察技术和建设技术评价值都属于高度脆弱，运行技术和设计技术指标属于中度脆弱，说明勘察设计和建设过程中存在重大质量问题，符合水利部门出具的安全鉴定专家报告中工程质量等级为不合格的评价。

4)管理情况属于低度脆弱，人员状况处于中度脆弱，社会脆弱性处于高度脆弱状态，其中社会脆弱性的脆弱源主要反映在经济脆弱性，说明该工程层存在经济问题，符合水利部门出具的安全鉴定结果。

4 结语

应用突变理论从原生脆弱性和外在脆弱性两方面因素对某中型水库的脆弱性进行评价，最终得到该中型水库脆弱性等级为高度脆弱，与相关水利部门出具的安全鉴定结果相符，证明该模糊突变模型应用于水库风险评价有效可行。由于水工建筑形式多样，其安全类别和评价标准存在差异，从而决定了水利工程脆弱性评价指标的非唯一性和变化性。因此，针对不同类别水利工程的脆弱性评价及其评价指标体系的优化构建，有待于进一步深入研究和探讨。同时，为获取更为准确的评价结果，水利工程管理部门应加强运行管理，建立基于实测资料和工情数据的水利工程脆弱性动态评价和自动预警系统，为水利工程安全管理提供理论依据和决策支持。