地物演化机制及演化过程的数学运算*

焦晨晨，钟业勋，胡宝清3，叶 彤1

(1.海军工程大学 导航工程系，湖北 武汉 430033；2.中国地质大学 地理与信息工程学院，湖北 武汉 430074；3.南宁师范大学 a.北部湾环境演变与资源利用省部共建教育部重点实验室，b.广西地表过程与智能模拟重点实验室，广西 南宁 530001)

0 引言

地物演化是普遍现象。从自然科学物质运动的角度看，它是物质运动的一种形式，在不同的时空显示出不同的状态；从社会科学和人文科学的角度看，则可发现许多地物的演化是人类有目的的意识行为的结果，而且这种基于主体意图的地物演化更为明显和普遍[1]。高铁、路网、水利设施，城乡建设、农田规划、植树造林、防沙治沙等工程造就的地物，无不是人类主体意图的物化，处处都打上了人类改造自然，改善人居环境和改造社会的烙印[2,3,4]。数学是用来描述众多现象的语言[5]。现实世界中的数量关系和空间形式，都可以用数学语言进行表达和描述[6]。从数学的角度看，地物演化是质和量的对立统一，是质和量的互变[7]。波恩说：“符号是深入到现象背后的自然实在里去的方法的一个必不可少的部分”[8]。符号化思维是科学思维最高级的形式，它是提高科学思维确定性的形式手段；它使科学思维具有可比较性，为科学思维从普遍性、深刻性上把握对象本质提供了保证[9]。鉴于地物的演化的普遍性和广泛性，以及目前论述其演化机制和表达其演化过程，探讨其数学表达的文献尚为少见，本文从点集拓扑学的原理，从点集变异引发的地物的量变、质变乃至区域的地类组成和结构的变换的角度，探讨地物演化的机制和数学本质[10,11]。

1 变异点集

定义1(消亡型点集)

∃ei≠∅∈X,ti=(t2-t1)∈ei∧ei(t2)=∅⟹ei(t′)t,t,t′∈ti,

(1)

则称ei为消亡点集，满足式(1)的演化称为消亡型演化，记作Δ-。

定义2(增长型点集)

∃qk∉X∧qk(t1)=∅，tk=(t2-t1)∈qk⟹qk(t′)>qk(t)|t′>t,t,t′∈tk,

(2)

则称qk为新生点集，满足式(2)的演化称为增长型演化，记作Δ+。

定义3(地物的演化)由于某种地类ei的消亡必定导致异质地类qk的新生，两者有下列蕴含关系：

∃ei∈Δ-∈A1⟹f(ei)=qk∈Δ+∉A1∧qk∈A2,

此时称ei和qk为相关地物，A2称为A1的演化。

定义4(变异速率)消亡型点集ei从非空集到空集的演化所需的时间愈短，其消亡的速度就愈快，所以变异速率为消亡地物存在的时间ti的倒数，即

vi=1/ti。

在ti内的不同时段(t,t′)∈ti，可能会有不同的速率，就像某项工程在不同的时段会有不同的进度一样。ei的消亡体现为地物的变异，所以变异速率等同于ei的消亡速率。显然，在保证工程质量的前提下，人们都会想方设法追求高的变异速率，也就是提高效率。

突发的自然灾害，如火山爆发、地震、泥石流、水灾等的发生地的破坏性过程及灾后重建，都呈现出很高的变异速率[12,13]。某些需要突击完成的建设任务，如2020年武汉在抗击新冠肺炎疫情中方仓医院的建设，对被自然灾害破坏的道路或桥梁的抢修重建等，都显示了极高的变异速率。

2 地物消长零和律

定律1(地物消长零和律)消亡地物伴生新地物的必然性、同时性、历时性、渐进性和消长代数和恒为零，称为地物消长零和律，即：

∃ei∈Δ-∈X⟹∃qk∈Δ+∈Ys.t. (Δ-ei+Δ+qk)=0|i≠k∨i=k。

(3)

式(3)中的qk便是由ei消亡而伴生的新地物，也是ei的覆盖。

任何地物的消亡必然导致另一异质地物填充其空间，这就是地物消亡和新生的必然性和同时性。这种新旧交替大部分属于异质(i≠k)的交替或覆盖。消亡地物ei的性质，与其从属的基本点集的性质相同，而新地物qk的性质，则取决于自然原因破坏情况或人们改造自然的人为设定。前者如火山爆发、地震、泥石流等，那是居民地、道路等本来为人使用的设施ei突然被难以预见的山体和泥土qk所覆盖。而灾后重建和人们计划之中的各种建设，则是人们将原来存在但并不令人满意的特定区域内的相关地物ei刻意消除，代之以按人们的意志创造的新地物qk。地图表示与客观实际的两个基本要素有关，即位置及其上面的特征。位置仅指二维平面上的位置[14]。而三维空间中的新地物在地球面上的位置，也就是它在地球面上的投影，在这个意义上，与旧地物在地面上的投影完全一致，这就是所谓的覆盖。如qk为某工厂，它是在某块荒地上兴建的，当新工厂竣工时，工厂所覆盖的地块便完全失去了荒地的性质。包括工厂的任何建筑或设施的兴建，都需要一定的时间，也就是所谓的工期，这就是地物演化的历时性和渐进性。不同地物之间总存在着或明显或隐蔽的边界，通过观察边界的变动可以发现地物在时空中的演化。对于地类性质的变更，也容易从相邻边界的变动中判断相关地物的扩、缩、消、长。由于演化空间的恒定不变，任何地物的缩小必定有等量的异质地物充实其空间，始终以代数和为零的规律确保演化空间的恒定性，这就是地物消长零和律。在以地物在地球面上的投影来确定其位置的测绘规则下，地物消长零和律主要体现在新旧地物的投影完全相同上。也就是说，在两者投影完全相同的情况下，其位置上面只反映地物的性质特征，而与这一维度上的量值无关。例如，在某块荒地上建房子，使地类由荒地变成了居民地。无论这居民地房子是高楼大厦还是平房，都不改变地块的居民地性质。由于时空的连续性，地物的演化具有历时性和渐进性[15]。

X上存在具有变量性质的消亡点集ei∈Δ-，是导致与之相关的基本点集演化的关键，因此，在X上有多少这种变量ei∈Δ-，是关系到X→Y演化的复杂性以及两者差异度的重要因素。例如，经济发达地区，各种各样的建设项目的开工、竣工引发的地物变化日新月异。而山区或相对落后的地区，就不及发达地区。地物的演化，首先是与变量ei相关地区的地物发生演化。

3 区域地类组成和区域结构的演化

4 从基本点集到目标点集的演化模式

定义5(结构点集和目标点集)设A,B,C∈X|ia∈A,ib∈B,ic∈C∧ia≠ib≠ic，为X上的基本点集，ei≠∅∈Δ-，ei的消亡同时会导致异于ei的地物qk的新生，ei的消亡和qk的新生过程具有同时性、历时性和渐进性。ei称为结构点集。ei与基本点集A,B,C∈X在变换f下的运算结果称为目标点集。从属于Y的不同的目标点集的集合A2,B2,C2∈Y便是A,B,C∈X的演化的结果。

定义6(地物演化的一般模式)设A,B,C∈X|ia∈A,ib∈B,ic∈C,ia≠ib≠ic，为X上的基本点集，结构点集ei=(A∩B∩C)∈Δ-∈X，在ei逐渐消亡的过程中新地物qk逐渐生成，当ei=∅时qk完全生成。其演化模式为

ei∈Δ-∈X⟹f(ei)=qk∈Δ+,ei=∅⟹(A2∪B2∪C2)∪qk=Y|i∈I,k∈K。

(4)

式(4)中i的标号集I和k的标号集K，以及基本点集A,B,C的目标点集A2,B2,C2的任意性，使任何区域X中的相关地类A,B,C，经地类赋值后通过有限的运算，总能实现到目标点集A2,B2,C2∈Y的变换。由于消亡地物ei和新生地物qk的边界相同，即b(ei)=b(qk)，而b(qk)又与任意闭曲线同胚，即b(qk)≈l，所以可对任意以闭曲线l为边界的闭集的消长进行表达。由于存在函数关系：

A2=f(A,eiA),B2=f(B,eiB),C2=f(C,eiC)|eiA∈A,eiB∈B,eiC∈C,

所以可对Y上的点集的相互关系和状态进行表达。本地物的演化的一般模式对地物从X到Y的演化具有很强的描述和解释功能。图1为地物演化的一般模式。

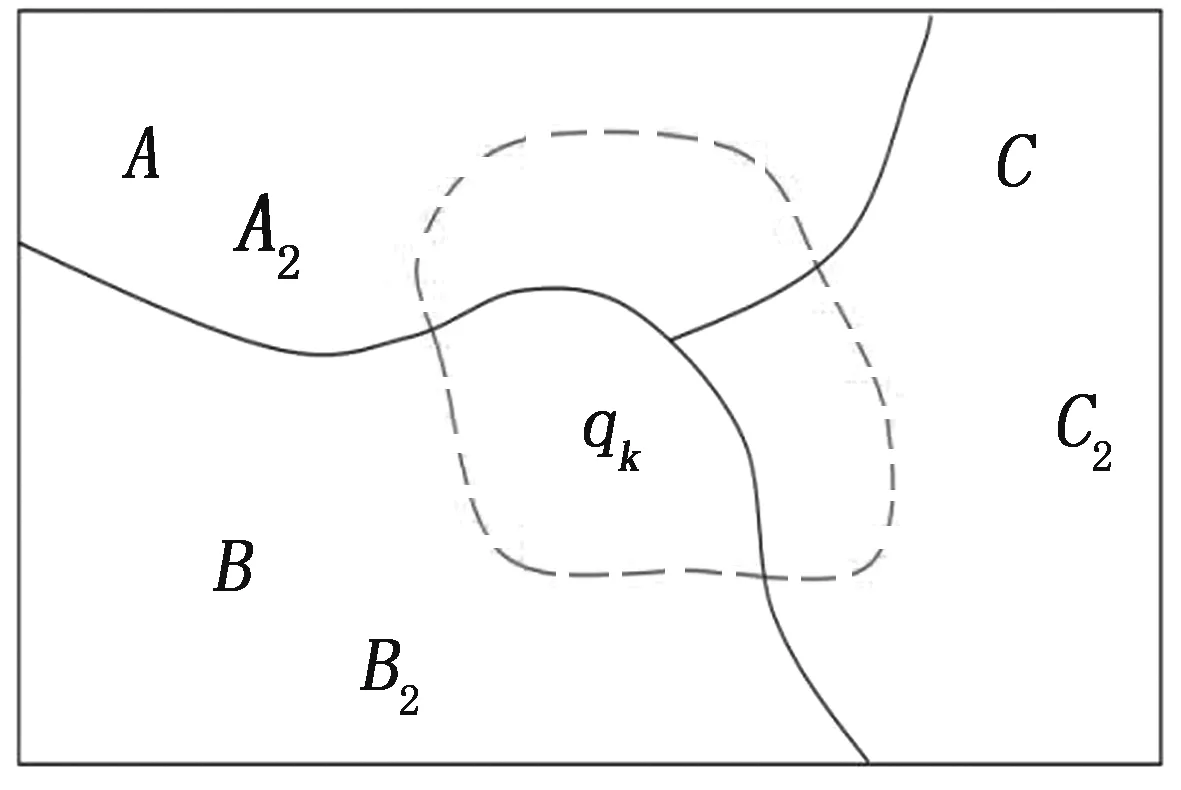
图1基于结构点集消长的地物演化

例如，qk是一个飞机场，那么ei就是飞机场qk覆盖的地类，即基本集合A,B,C的交集(ei可以是多种地类的集合)。飞机场建成后，交集处的某些地类由ia,ib,ic质变成了qk覆盖的地类，原来的基本集合A,B,C因结构点集eiA,eiB,eiC的质变而演化为A2,B2,C2，并同新生的qk一起成了Y的构成元素。

由于演化遵循Δ-en+Δ+qk=0的地物演化零和律，ei的减少和等量的qk的增加都会引起相关点集的量变和质变，这种消长代数和为零的关系存在于每一时刻，这就是同时性；而qk对ei的替代或覆盖有个过程，就像每一项工程建设都有一定的工期一样，这就是历时性和渐进性。由于哪里有演化哪里就必须遵循地物演化零和律，而地物演化零和律又必然引起相关地类的量变和质变，从而使地物演化具有必然性，这就是地物演化的内在逻辑。

5 区域的演化实例

图2中，设t1时刻的区域X的地物类型和结构(实线)为

1.2.1 细胞培养 MDA-MB-231细胞所用培养基为含10%新生牛血清，100 U/ml青霉素和100 μg/ml链霉素的DMEM培养基，37 ℃ CO2培养箱中培养传代。

X=A∪B∪C∪D∪E∪F.

到t2时刻X区域演化为Y，其地物类型和结构(虚线)为

Y=A2∪B2∪C2∪(D2-L2)∪(E2-1E2-2)∪

(F2-1F2-2)∪G2∪(H2-1H2-2)∪L2.

图2中ei为消亡点集，ei的消亡导致qk的新生。点集qk在本例中各有不同的质变，并与其从属的基本点集有不同的关系和运算[18]。各基本点集的演化过程如下。

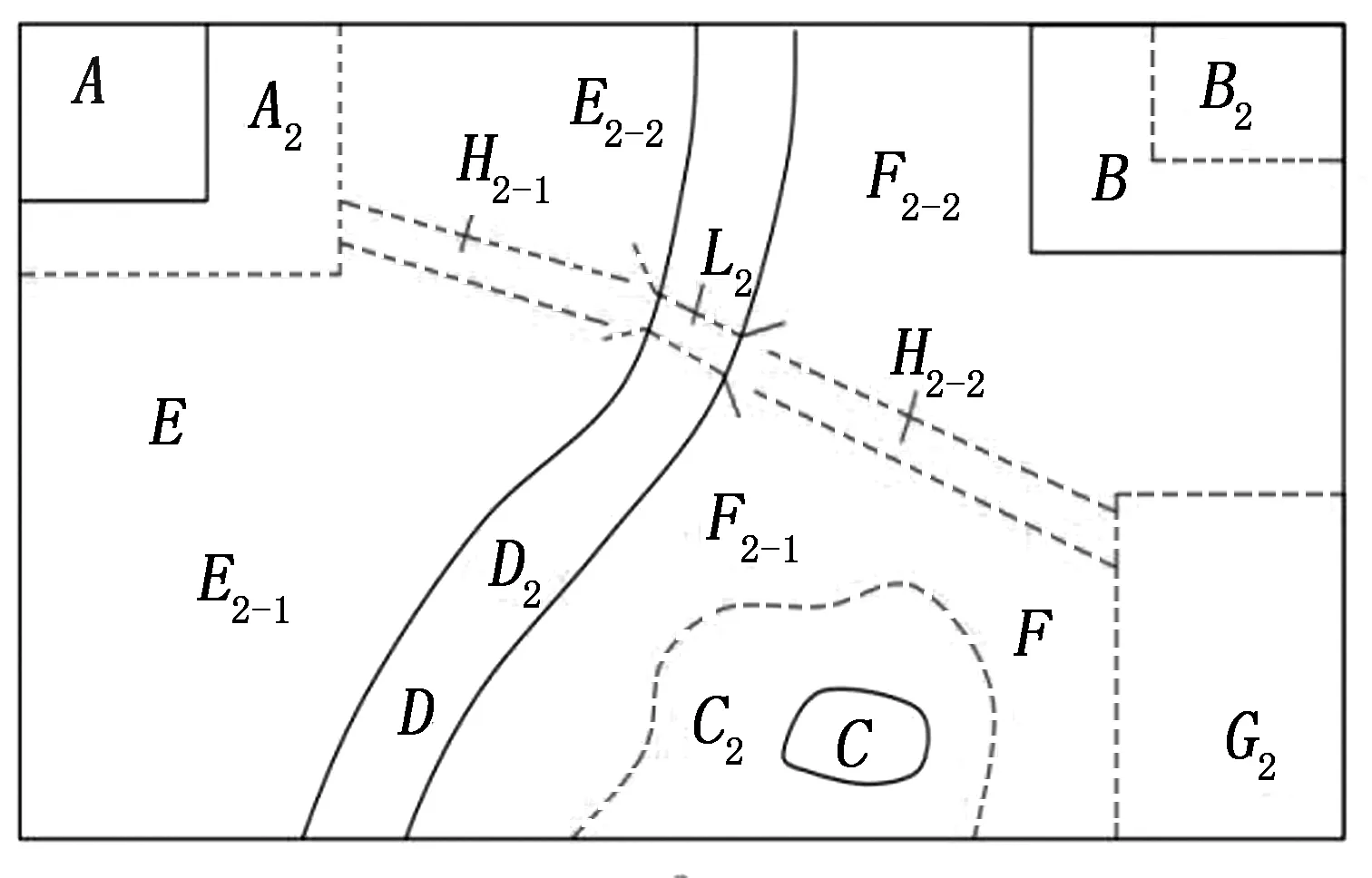
图2区域地物演化示意图

(1)ei∈E消亡并质变后，使A扩大为A2，E缩小为E′：

ei∈E⟹f(ei)=qks.t.E′=(E-ei)∧A2=(A∪qk)∈Y.

(5)

(2)ei∈B的消亡使B缩小为B2，ei质变后又使F扩大为F′：

ei∈B⟹f(ei)=qk∧F′=(F∪qk)∧B2=(B-ei)∈Y.

(6)

(3) 包含C的消亡点集ei质变后生成C2：

∃ei⊃C∈F′⟹f(ei)=qk=C2∈Y.

(7)

(4) 由于D上在Y中有新地物L2，故需减去L2所占的面积：

∃ei∈D⟹f(ei)=qk=L2∈Y∧D2=(D-ei)∈Y.

(8)

(5)ei∈F′的消亡导致G2的新生：

∃ei∈F′⟹f(ei)=qk=G2∈Y.

(9)

(6)ei∈E′的消亡导致H2-1的新生：

∃ei∈E′⟹f(ei)=qk=H2-1∈Y.

(10)

(7)ei∈F′的消亡导致H2-2的新生：

∃ei∈F′⟹f(ei)=qk=H2-2∈Y.

(11)

(8)E′与H2-1的差集等于E2-1和E2-2的分离并且同属于Y:

(E′-H2-1)=(E2-1E2-2)∈Y.

(12)

(9)F′与C2,G2,H2-2的差集等于F2-1和F2-2的分离并且同属于Y:

(F′-C2-G2-H2-2)=(F2-1F2-2)∈Y.

(13)

由基本点集A,B,C,D,E,F构成的X，经演化后变成了由目标点集构成的Y,在Y上，A-A2,B-B2,D-D2,E-E2-1,E2-2,F-F2-1,F2-2依然是性质相同的地物，但产生了量变。C已完全消失，它原来所占的面积完全包含在新地物C2所占的面积之中。而G2,H2-1,H2-2和L2都是X上没有的新地物。式(5)至(13)分别表示了各基本点集的整个演化过程。

6 本项目在地学研究中的理论创新和应用价值

科学产生于人类的动机，它是由人类创造、更新和发展的。它的规律、结构和表达，不仅取决于其所发现的实在的性质，还取决于完成这些发现的人类本性的性质，所以科学是人学[19]。人文地理学对人类活动所创造的人文现象进行了深入的研究并获得了许多成果[20]。生态学定律关于每种事物都与其他事物相互联系和相互交融，对自然界的任何侵犯都会产生多效应原理，强调了生态平衡问题不容忽视[21]。其实人类行为对生态平衡的破坏已有许多教训：森林具有保持水土，涵养水源的作用。乱砍乱伐会导致水土流失，土地沙化，洪水泛滥。矿山开采、劈山修路、切坡建房等大规模工程和不适当的人类行为会引发山体滑坡、岩土体崩塌、泥石流等地质灾害[22]。城市的快速发展、各种建设项目的开工竣工，使地表面貌日新月异。为治理环境，保护生态和经济的可持续发展，从中央到地方各级政府部门出台了限制污水排放，清洁河流，退耕还牧，退耕还林，植树造林等举措，这些举措的实施也是一种引发地物演化的重要原因。自然原因或人类有目的的意识行为引发的地物演化，都是地学研究中的重要问题。本文以点集变异的观点，应用点集拓扑学的数学工具和地物消长零和律，对地物演化进行了数学表达和定量描述，这是关于地物演化问题的理论创新。本文给出了地物从基本点集X到目标点集Y的演化模式，由于点集符号具有代数符号的性质，因而对任何具体的区域经地类赋值后都可对其演化过程进行描述和解释。故本演化模式具有很强的解释功能和应用价值。

7 结论

地物的演化是普遍现象。无论是自然原因还是人们按自己的主体意图实施的各种工程建设项目，都会导致地物的演化。地物的演化的本质是点集变异。某种地物ei的消亡必定导致另一种异质地物qk的新生，而且两者在地面上的投影完全一致。新生地物qk表现为对消亡地物ei的覆盖。这种地物的新旧更替满足地物消长零和律。从基本点集到目标点集的演化模式，因符号具有代数符号的性质，对于任何具体的区域，对地类赋值后都能对其演化进行合理的解释。通过实例，阐释了地物演化的运算过程和演化机制，论述了本文的理论意义和应用价值。