基于误差分级迭代法的基坑变形预测
2021-07-29刘晶磊张国朋张冲冲
刘晶磊,张国朋,张冲冲,张 楠
(1.河北省土木工程诊断、改造与抗灾重点实验室,张家口 075000;2.河北建筑工程学院土木工程学院,张家口 075000;3.河北省寒冷地区交通基础设施工程技术创新中心,张家口 075000)
目前,岩土工程领域存在大量复杂问题,大多数学者采用计算机智能和软件分析进行解决。王小生等[1]利用最小二乘法对基坑周边建筑物沉降预测结果具有工程指导意义;谢洋洋等[2]采用量子粒群灰色支持向量机与遗传小波神经网络进行优化,并预测基坑变形具有较高拟合性;徐文杰[3]利用指数曲线、双曲线、灰色模型建立误差绝对值预测组合模型,提高神经网络的预测精度;李思慧等[4]通过将局部均值分解量子群优化算法与最小二乘支持向量机组合模型进行预测;Srivastava等[5]通过正则化方法对神经网络进行优化,细化网络的预测效果;Chen等[6]采用遗传算法和模拟退火算法相结合的方法来优化网络的权值和偏差,修正后的模型可以加快学习速度,提高预测精度;宋楚平[7]通过遗传算法对模型权重初值进行优选,避免模型陷入局部最小值;吕磊等[8]利用灰色神经网络模型和模糊神经网络建立模型,提出模糊神经网络模型更适合长期预测;孙曦源等[9]通过对实测数据进行归一化处理和统计分析得出基坑施工诱发周边地表沉降的经验预测方法;贾哲等[10]借助Elman神经网络预测模型,在修正前后的预测效果优于BP(back propagation)神经网络模型;钟国强等[11]利用混合蛙跳算法和广义回归神经网络模型进行深基坑预测;周星勇等[12]引入自适应增强算法对遗传神经网络预测模型进行改进,平均绝对百分比误差(mean absolute percentage error,MAPE)、平均绝对误差(mean absolute error,MAE)、均方误差(mean square error,MSE)3项精度指标得到提高;马征[13]应用MAPSO-LSSVMS数学模型对基坑周围建筑物进行沉降预测,模拟值与实际值具有较高的预测精度。
上述研究通过对BP神经网络的优化从而达到提高学习效率和收敛速度的目的。BP神经网络在预测方面存在诸多问题,结合诸多学者的研究结果需要对BP神经网络模型进行优化,从而提高预测精准性能。大多数学者采用神经网络进行预测基坑变形,鲜有学者采用误差分级迭代法进行基坑变形预测,误差分级迭代法在气温预测[14]、沥青混合料抗剪强度预测[15]方面均有研究,而在基坑变形预测方面研究较少。人工神经网络时间序列的有效预测有两种方法:多周期预测性能的迭代预测方法和直接预测方法[16]。而通过迭代法将预测误差添加到数值预测中,加上或者减去,预测精度得到改进[17]。现采用误差分级迭代法对BP神经网络进行优化,以期研究成果在基坑变形预测方面与BP神经网络具有更优的性能。
1 基坑变形预测方法
通过对文献[18-19]研究结果的总结发现,影响基坑变形主要因素有地质条件、支护结构、基坑平面尺寸及开挖深度、施工工程和场地周边环境、地面超载和震动荷载。影响基坑变形因素主要以上述5种因素研究居多,基坑变形过程中表现为单个因素或多个因素共同作用下对变形产生较大影响,需要综合考虑多种因素对变形的相互作用。采用线性函数不能准确反映因素间的影响程度及影响过程,因此采用非线性函数解决多因素间影响基坑变形尤为重要。
1.1 BP神经网络
BP神经网络具有极强的非线性映射能力,隐含层的数目如果足够多,可以任意精度逼近一个非线性函数。BP神经网络通过与预先存储信息和学习机制进行自适应训练,这种能力使其在预测方面具有重要作用。BP神经网络具有优化计算能力,本质属性是解决非线性优化问题,在已知的约束条件下寻找一组参数组合,使该组合确定的目标函数达到最小。采用最速下降法的学习规则,通过反向传播来调整网络的权值和阈值,使网络的误差平方和最小。拓扑关系如图1所示。

图1 神经网络拓扑关系Fig.1 Neural network topology relationship
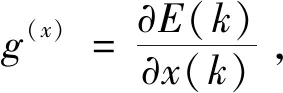
(1)
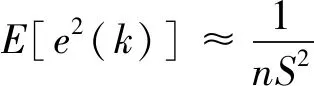
(2)
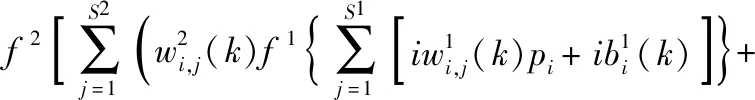
(3)
(4)
式中:e为误差;S为样本数;t为期望输出值;a为学习速率;f为激活函数;w为连接权值;i、j为神经元;b为截距项;p为输出层单元数。
1.2 误差分级迭代法
由于神经网络模型在实际应用过程中存在局部最小点、学习收敛速度慢、隐层节点个数选取缺乏统一标准等问题,胡伍生等[20]在神经网络的基础上创新性地提出误差分级迭代法,可以有效地解决神经网络模型在应用过程中存在的问题,误差分级迭代法是将学习误差ε0进行分级,将ε0分为n级,分级公式为
εi=2n-iε0,i=1,2,…,n
(5)
εi=(n-i+1)ε0,i=1,2,…,n
(6)
再依次取ε1,ε2,ε3,…,εn(εn=ε0)作为收敛控制参数让神经网络对学习集样本进行学习训练。如式(5)、式(6)所示。当第n级误差ε0迭代收敛后,则网络的学习过程就宣告结束。误差分级迭代法的程序如图2所示。
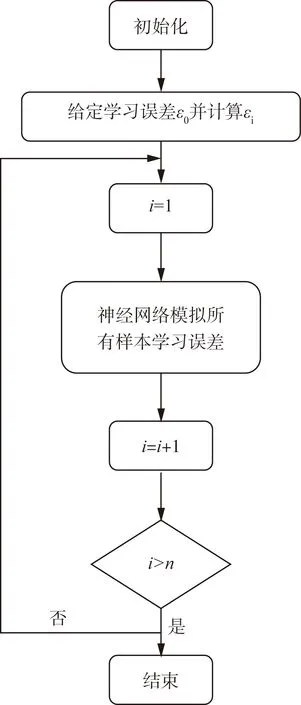
图2 误差分级迭代法程序Fig.2 Error classification iteration method procedure
2 参数模型建立
2.1 样本输入
(1)输入层元素取3,分别采用前三天实测数据进行预测。
(2)隐含层节点数选取缺少参考依据,结合诸多学者的经验值,并结合现场量测数据进行计算机仿真计算。现采用实测数据进行试算最终确定隐含层节点数。
(3)输出层元素取1,为时段水平位移;累计水平位移可通过对所有时段水平位移相加而得到。
经过分析研究,确定BP神经网络模型为3层结构。
2.2 隐含层节点数
隐含层参数的选取对神经网络的预测结果影响很大,采用不同隐含层节点进行模型计算,隐含层节点数N采用6、9、12、15共4种,对样本数据进行训练和预测。
隐含层节点预测误差如图3所示。图3中隐含层节点数选取为6、9、12、15,由图3可知,节点数为9、12时误差值与0差值之间存在较大差距,节点数9虽然与0差值之间较近,但存在个别点的数值偏大,影响最终的结果,故选用节点数为6,进行变形预测,最终确定的神经网络模型的结构为Model[3×6×1]。

图3 隐含层节点预测误差Fig.3 The prediction error graph of hidden layer nodes
3 工程实例仿真计算
上海市某深基坑工程设置大量监测点,训练样本采用支护结构水平位移监测数据,采用7 m深度处的数据作为样本,表1所示为实测数据,共21组样本数据,第1~16组作为训练样本,第17~21组作为预测样本。训练样本见表2,预测样本见表3。采用3个输入单元和一个输出单元的神经网络结构,将神经网络的预测值作为误差分级迭代法的输入值,建立误差分级迭代模型进行基坑变形预测。训练样本来自文献[21]。
编写运行程序,通过对训练网络练习,并将预测样本输入训练网络进行预测,将神经网络预测值结果作为误差分级迭代的输入值进行再次网络训练,输出最终的结果为经过误差迭代分级法处理后的预测值。由表4神经网络预测结果可知,经过误差分级迭代法处理的预测值结果相对误差值与实际值基本吻合,并与文献[21]中的径向基神经网络(RBF)预测值形成对比,预测精度高于文献[21]的径向基神经网络(RBF)方法。
从表4中可以得出,误差分级迭代法对基坑变形预测具有很高的实用性,误差分级迭代对基坑支护结构的位移具有可行性,预测精度符合工程实际需求。

表1 部分深度处支护结构水平位移[21]Table 1 Horizontal displacement of supporting structure at partial depth[21]
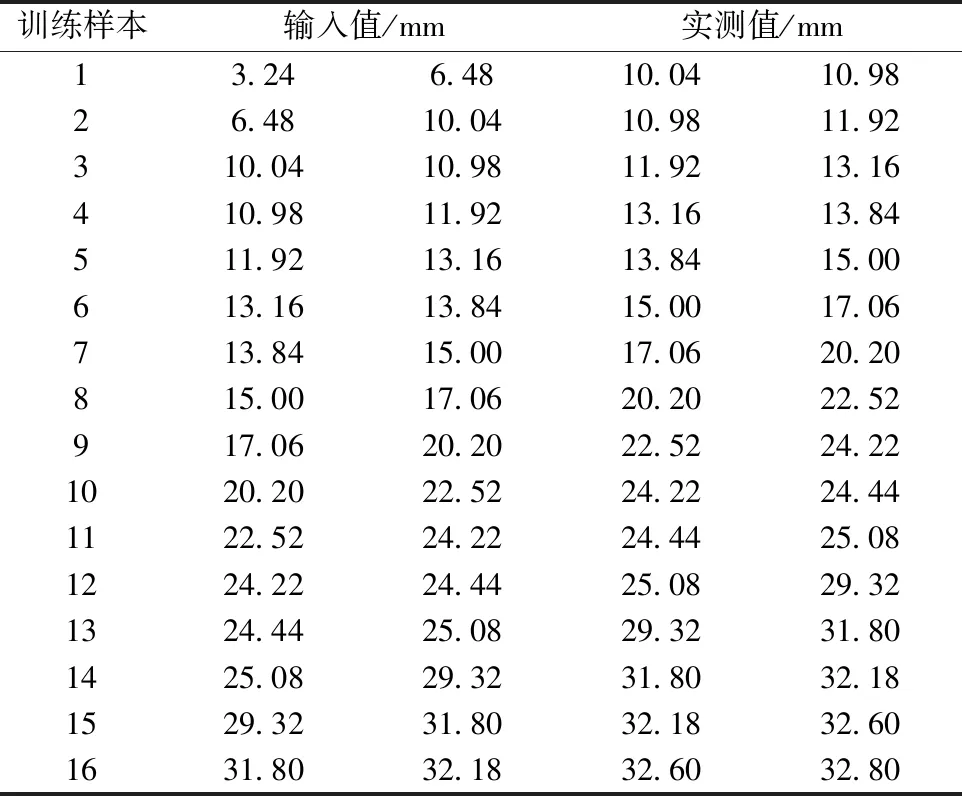
表2 训练样本Table 2 Training samples
由图4可以看出,基于误差分级迭代法预测值与实际值比较接近,最大误差为0.96%,而文献[21]中径向基神经网络的预测值与实际值差值较大,最大误差为3.76%,本文误差迭代法能够很好地降低误差,提高预测精度。通过对人工神经网络预测结果的对比分析可知,误差分级迭代法的预测效果优于BP神经网络、GA-BP遗传神经网络、RBF神经网络的预测效果。
误差分级迭代法与神经网络、径向神经网络相比,通过将误差进行迭代,进而将误差差值逐步降低,实现误差的最小化,最终达到全局误差最小值的目的,而神经网络、径向基神经网络只是通过隐含层函数进行运算,无法实现全局最优的问题,故误差分级迭代法在基坑预测领域具有预测精度高、实现全局最优的特点。
4 结论
选取上海市某深基坑项目变形观测数据,建立误差分级迭代优化神经网络模型,通过与深基坑实测数据进行对比,得出以下结论。
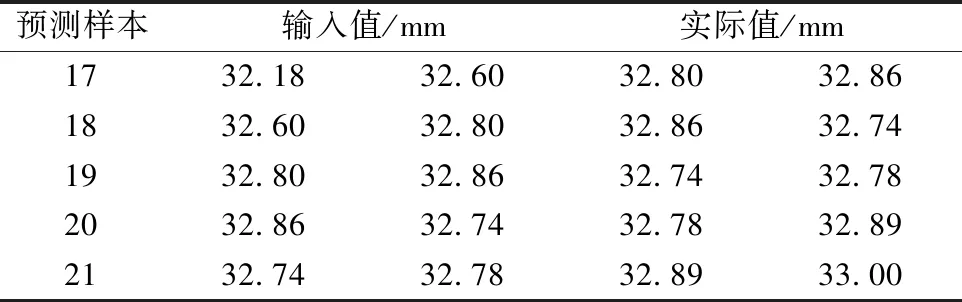
表3 预测样本Table 3 Forecast sample

图4 预测值与实际值比较Fig.4 Comparison of predicted value and actual value

表4 神经网络预测结果对比分析Table 4 Comparative analysis of neural network prediction results
(1)误差分级迭代法在应用于基坑变形预测方面具有较高的精准性,优化后的BP神经网络模型降低初始权值和阈值随训练样本的影响,提高了模型预测精度。
(2)采用误差分级迭代后基坑变形预测性能提高,与实际观测数据最大误差为0.96%,具有很高的实用价值。
(3)经过误差分级迭代法处理的基坑变形数据与径向基神经网络处理的数据在预测精度方面提高3.5%,同时达到误差全局最优的预测目的,预测结果更符合工程实际,为工程预测提供新的方法和经验。
