上下料机器人关节速度规划
2021-07-29李金良舒翰儒杨学顺刘阿健
李金良,张 斌,舒翰儒,杨学顺,刘阿健
(山东科技大学机械电子工程学院运输与提升重点实验室,青岛 266590)
随着中国对工业 4.0 高科技战略计划的重视与不断深化,上下料机器人技术进入了快速发展的阶段,在解决劳动力资源短缺问题、节省人力成本和提高生产效率等方面具有巨大的发展空间[1]。为了保证在上下料机器人关节的运动平稳性,需要利用专门的加、减速控制算法来对机器人关节进行平稳精准的速度控制[1]。
梯形加减速控制算法[2-3]具有运算简单的优点,但会因为加速度突变导致机器人在运行过程中产生冲击。Hu等[4]对此做出了验证。S形加减速控制算法具有加速度不发生突变的优点被广泛的应用。陈雪[5]对五阶S曲线加减速控制算法进行优化并进行仿真验证;李振娜等[6]将S型加减速控制算法分为4种类型,设计了插补算法并在实验平台上进行实验验证;张树刚等[7]提出了一种应用于包装堆垛机器人的三次多项式S型加减速控制算法并进行仿真与试验验证。这些研究中的S型加减速控制算法均存在运算复杂并且加加速度不连续的弊端。
为此,对4R上下料机器人进行研究,利用Solidworks和ADAMS的对上下料机器人进行联合仿真[8],分析了梯形、7段S形两种加减速控制算法在虚拟样机中仿真所得到的结果并提出了一种新型的S形加减速控制算法,以期在确定上下料机器人运动轨迹的合理性后,保证运动速度曲线的光滑,较少速度冲击所引起的机器振动,为实际生产提供参考。
1 上下料机器人模型的建立
1.1 结构分析
4R上下料机器人属于串联机器人,主要由底座、4个连杆和4个旋转副组成,整体图如图1所示,其中,轴1旋转范围为-170°~170°,最大角速度450(°)/s;轴2旋转范围在-70°~125°,最大角速度150(°)/s;轴3旋转范围在-75°~20°,最大角速度250(°)/s;轴4旋转范围在-170°~170°,最大角速度450(°)/s。上下料机器人通过末端吸盘进行物料抓取,伺服电机对轴关节进行驱动完成搬运动作,且各个轴关节运动互不干扰。

图1 上下料机器人三维模型Fig.1 3D model of loading and unloading robot
1.2 虚拟样机模型的建立
在三维实体建模中,ADAMS在这一方面表现稍显不足,因此利用专业的CAD软件进行建模。首先采用Solidworks对主要的运动部件进行实体三维建模并更改为*.x_t格式导入ADAMS中[9-11],之后对导入的模型进行质量、材料、颜色等属性重新定义,最后进行运动副和Y轴负方向重力加速度的添加。
此时需要利用ADAMS中tools/model verify命令对所建立的模型进行检查,并得到反馈模型相关信息的对话框。最后设置适当的步长和仿真时间,检验模型在自身重力作用下所建立的模型是否正确。
2 加减速控制算法分析
上下料机器人在上下料作业中有很多种加减速度控制算法,不同的加减速度算法会使机器人产生不同的运动效果。建立梯形、S形加减速控制算法模型进行仿真,分析出对上下料机器人末端运动平稳性的影响。
2.1 梯形加减速控制算法
梯形加减速控制算法分为3个部分[12-13]。如图2所示,系统在加速部分时,加速度为常数a0,速度V随着时间t的线性增大,在t1时刻为最大速度V0并开始匀速运动,此时为匀速部分,在t2时刻开始进入减速部分,加速度为常数-a0,速度V则随着时间t线性下降,在t3时刻速度降为0,所以速度表达式为
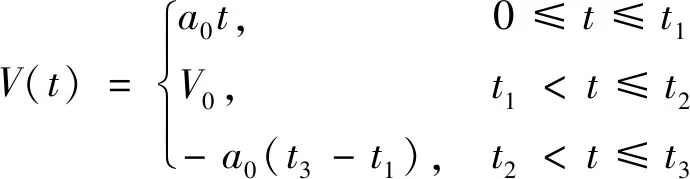
(1)
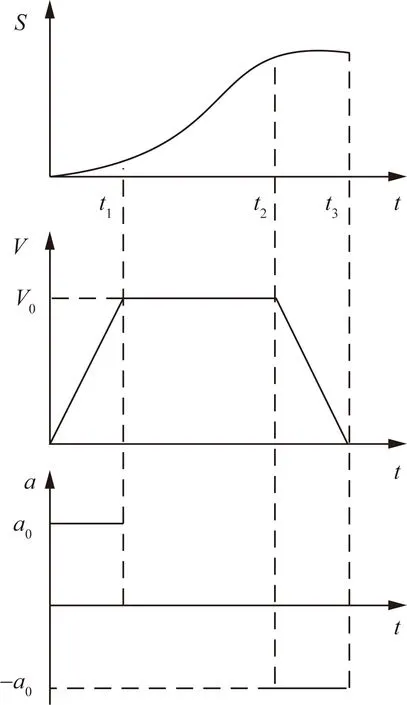
图2 梯形加减速控制算法Fig.2 Trapezoidal acceleration and deceleration control algorithm
在ADAMS中利用IF函数编辑为
IF(time-t1:a0* time,V0,IF(time-t2:V0,V0,IF(time-t3:-a0*(time-t3),0,0)))。
2.2 7段S形加减速控制算法
7段S形加减速控制算法是在梯形加减速的基础上,将加减速阶段各细化成3部分,整个控制算法分为7个部分:加加速部分、匀加速部分、减加速部分、匀速部分、加减速部分、匀减速部分和减减速部分。如图3所示,该算法的加加速度为常数,通过对加加速度的函数进行积分可以得到其加速度、速度函数,函数次数依次递增,这虽然对系统冲击小,有利于减小振动[14],但是运算过于复杂。
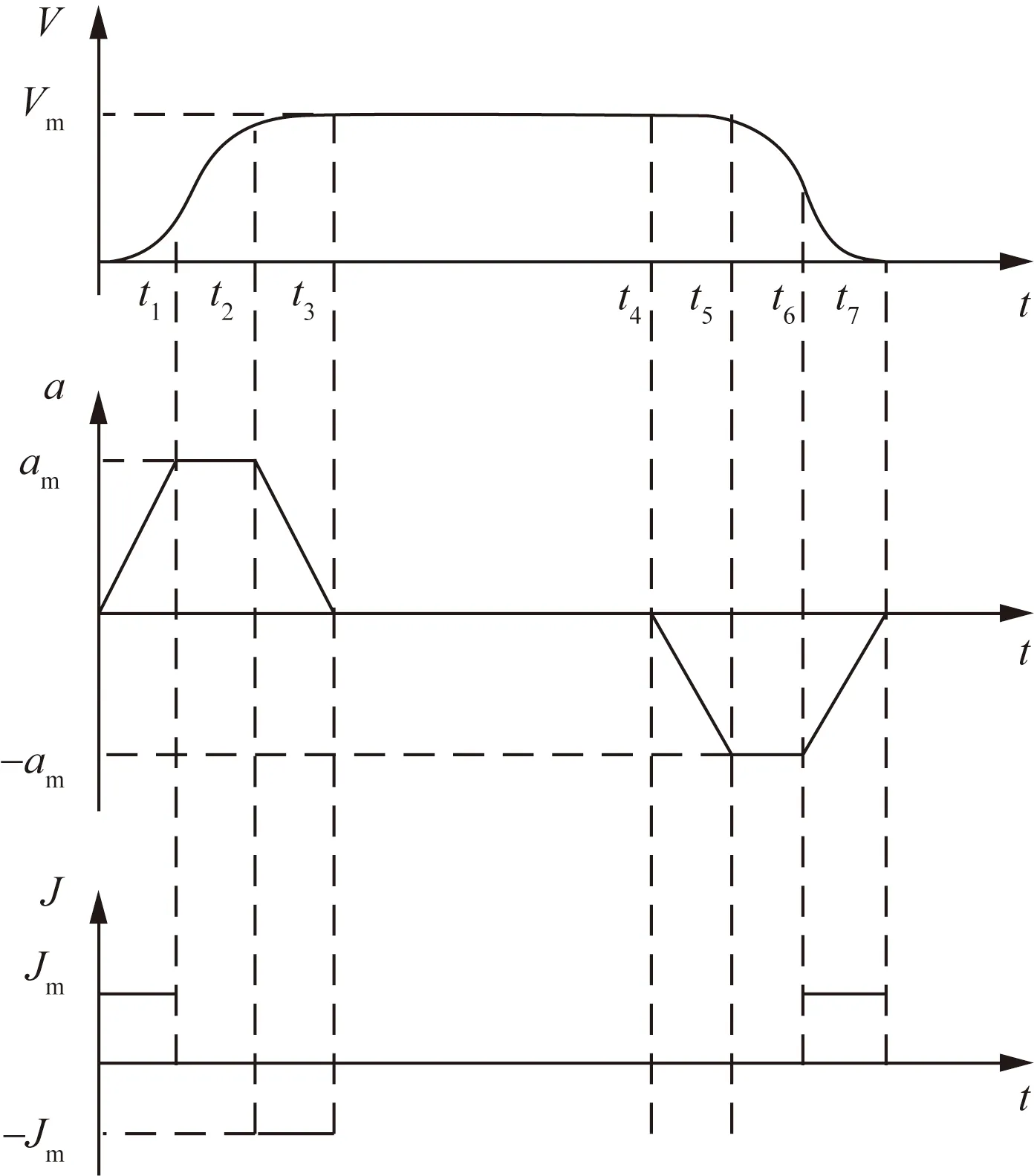
Jm为最大角加加速度;am为最大角加速度;Vm为最大角速度;ti(i=1,2,…,7)为各个阶段时刻图3 7段S形加减速度控制算法Fig.3 7-segment S-shaped acceleration and deceleration control algorithm
速度表达式为

(2)
式(2)中:Jm为最大角加加速度;am为最大角加速度;Vm为最大角速度;ti(i=1,2,…,7)为各个阶段时刻;Vi(i=1,2,…,7)为各个阶段时刻所对应的角速度。
在ADAMS中利用IF函数编辑为IF(time-t1:Jm/2* time**2,V1,IF(time-t2:V1+a*(time-t1),V2,IF(time-t3:V2+a*(time-t2)-Jm/2*(time-t2)**2,Vm,IF(time-t4:Vm,Vm,IF(time-t5:Vm-Jm/2*(time-t4)**2,V5,IF(time-t6:V5-a*(time-t5),V6,IF(time-t7:V6-a*(time-t6)+Jm/2*(time-t6)**2,0,0)))))))。
2.3 仿真结果分析
根据上下料机器人的实际工作状况和结构参数,在ADAMS中利用IF函数建立梯形、7段S形加减速控制算法对机器人的4个关节进行定义并将驱动类型设置为速度。在上下料机器人末端执行机构建立标记点MARKER_0作为测量点进行数据测量,End Time设置为1 s,Steps设置为1 000步。仿真结果如图4、图5所示。
图4所示上下料机器人在使用梯形加减速控制算法后,其末端执行机构的速度变化曲线不平滑,加速度变化曲线在多处存在突变现象,这会导致机器人关节处的伺服电机出现震动和噪声;图5所示上下料机器人在使用7段S形加减速控制算法的控制后,其末端执行机构的加速度突变的问题得到解决,对系统冲击小,速度变化曲线相对平滑,但加速度不连续的问题依然没有解决,这会直接影响机器人的运动平稳性和精确性,缩短机器人的使用寿命。
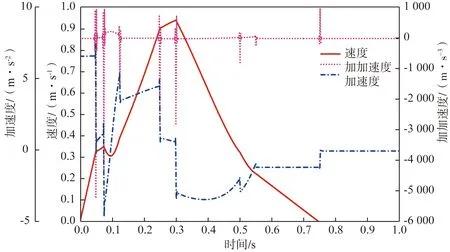
图4 机器人末端梯形加减速控制算法曲线Fig.4 Trapezoidal acceleration and deceleration control algorithm curve of robot end

图5 机器人末端7段S形加减速控制算法曲线Fig.5 7-segment S-shaped acceleration and deceleration control algorithm curve of robot end
3 新型的S形加减速控制算法
3.1 新型的S形加减速控制算法
新型的S形加减速控制算法是在轨迹规划的时候仍旧使用梯形的方法将整个运行过程分为3个部分,并计算出3个部分的执行时间,在插补控制时将当前插补周期带入余弦加减速控制算法的函数中,然后进行曲线拟合:
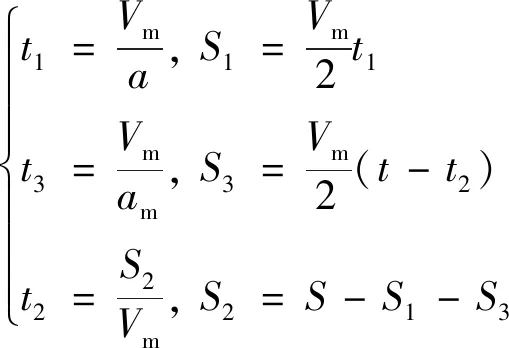
(3)
式(3)中:t1、t2、t3各个阶段的时刻;S1、S2、S3分别为3个阶段的位移。
在加减速时,以时间为变量通过式(3)拟合出对应的位置函数。图6为经过拟合后得到的速度变化曲线。
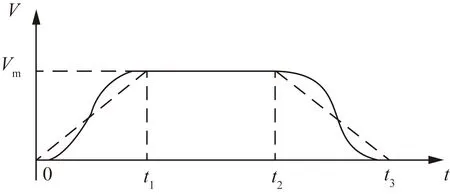
图6 新型的S形加减速控制算法速度变化曲线Fig.6 Speed change curve of new S-shaped acceleration and deceleration control algorithm
所对应的位移函数表达式为
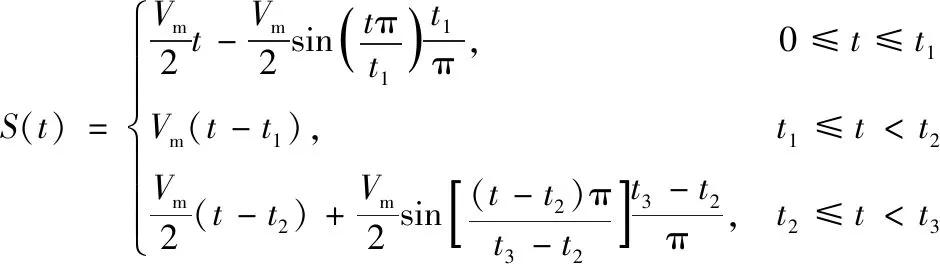
(4)
由此得出对应的速度函数表达式为

(5)
通过式(4)和式(5)可以清楚地看出,该控制算法可以有效地降低轨迹规划及速度前瞻时的计算量。
在ADAMS中利用IF函数编辑为IF(time-t1:Vm/2-Vm/2* cos(time*pi/t1),Vm,IF(time-t2:Vm,Vm,IF(time-t3:Vm/2+Vm/2*cos((time-t2)*pi/(t3-t2)),0,0)))。
3.2 仿真分析
为了验证新型的S形加减速控制算法的合理性,分别在机器人关节处设置驱动函数进行仿真,部分关节参数曲线如图7所示,上下料机器人在使用该算法后,机器人转动关节在作业时的角速度、角加速度和角加加速度的变化曲线平滑连续且没有发生突变。如图8所示,上下料机器人在使用该算法进行控制后,机器人末端执行机构的速度、加速度和加加速度变化曲线平滑连续且没有发生突变,成功地解决了加速度不连续的问题,有效地提高机器人运动的平稳性,比以上两种方法更适合机器人的精确控制。
4 结语
(1)利用Solidwords和ADAMS对4R上下料机器人进行联合仿真,能够直观地模拟出机器人的工作业过程,为上下料机器人的更深入的研究奠定了基础。
(2)通过机器人关节的速度规划仿真,分析出梯形加减速控制算法和7段S形加减速控制算法都会导致机器人关节受到的冲击和产生振动,为此提出了一种新型的S形加减速控制算法来提高其运动平稳性,并利用ADAMS和Solidwords对该算法进行了联合仿真分析。联合仿真的结果表明,该算法在运算简单的前提下,有效地解决了加加速度不连续的问题,提高了机器人的运动平稳性,为机器人进一步地优化设计提供了参考。
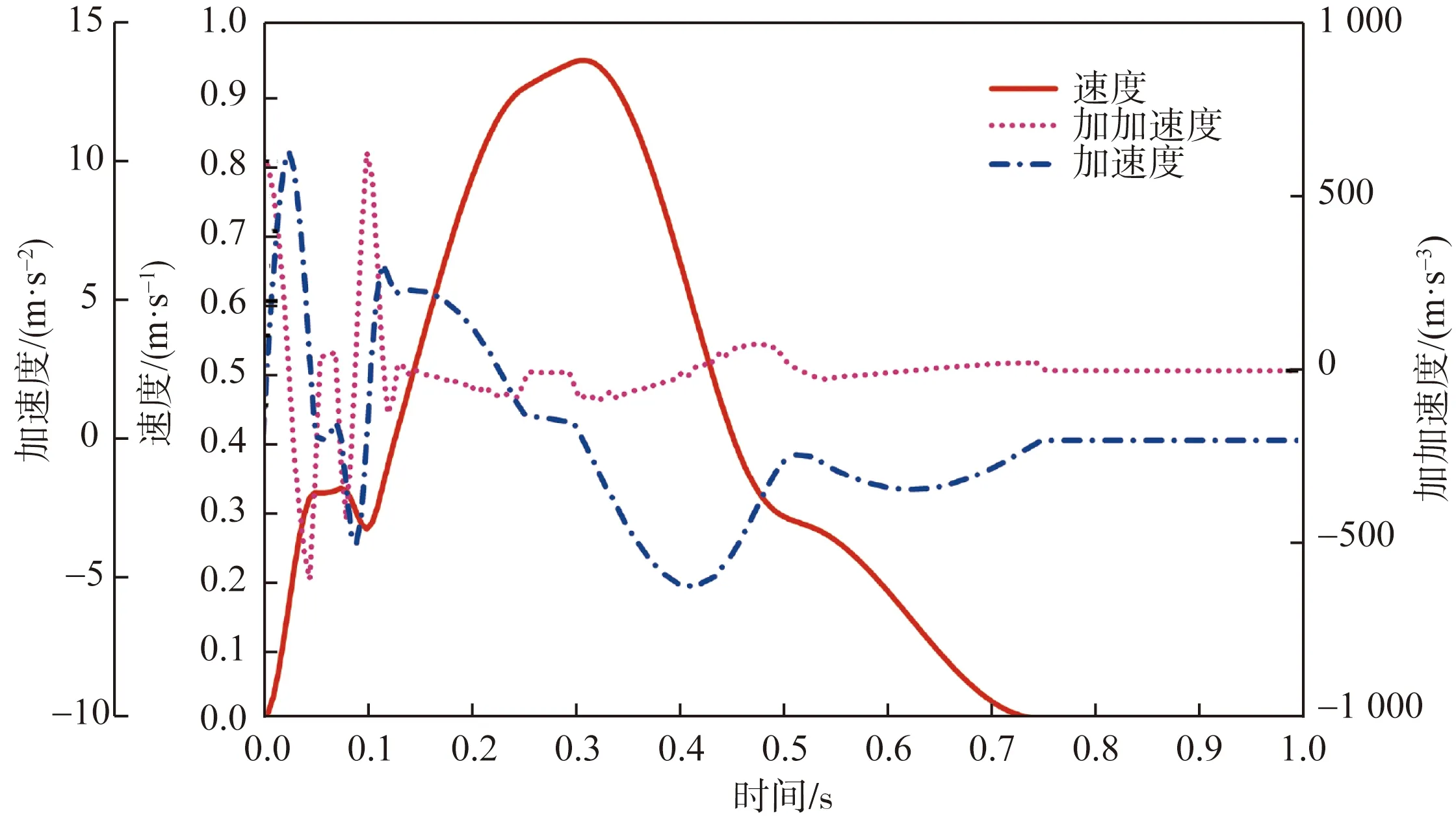
图8 机器人末端新型S形加减速控制算法曲线Fig.8 New S-shaped acceleration and deceleration control algorithm curve for robot end
