不同压实度花岗岩残积土的渗流模拟

王志兵，谈勋勋，王 远，孙 广，刘金明

(1.桂林理工大学土木与建筑工程学院，桂林 541004；2.广西岩土力学与工程重点实验室，桂林 541004)

花岗岩残积土作为一种路基填料，当其压实度不足时，会导致路基灾害或病害的发生。如2015年12月20日深圳光明新区，废土填埋场由于风化花岗岩压实度不足导致滑坡[1]。以花岗岩残积土作为路堤边坡的广佛肇高速公路多处出现浅层滑移、水毁、崩塌[2]。众多的路基病害与填料的压实度有紧密的关联。因此，研究不同压实度对花岗岩残积土渗透特性的影响不仅对实际具有应用价值，而且对岩土领域有理论意义。以往研究人员对土体的认识更多局限在宏观尺度上[3]，未从土体内部的孔隙分布、孔喉分布等微观结构特征考虑，导致无法研究渗流的微观影响因素[4]。

为了研究压实度对多孔介质微观渗流特性的影响，第一步是获得其孔隙空间结构分布特征。目前，获得多孔介质孔隙结构特征主流的研究方法有：压汞法(mercury intrusion porosimetry,MIP)[5]、氮气吸附法(nitrogen adsorption method,NAI)[6]、光学显微镜或扫描电镜法[7]、CT扫描图像法[8]。压汞法会产生“墨水瓶”效应且破坏土体的结构。氮气吸附法只能测量微小的孔隙。光学显微镜或扫描电镜法只能定性表征土体的局部孔隙结构。相比与其他方法，CT扫描图像法可以快速无损的获取样品孔隙空间结构参数，定量表征样品的孔隙空间结构，建立三维可视化模型[9-12]。

以往表征流体流动规律是建立在以达西定律为基础的宏观渗流方程上，由于CT扫描图像法的出现，通过CT扫描图像法提取孔隙网络模型，在获取样品孔隙空间结构的同时研究微米级流体输运特征[13-25]。由于土体孔隙结构复杂和计算机性能的限制，导致直接运用孔隙网络模型进行渗流模拟较为困难。中外学者多以流体力学的传统方法CFD及格子玻尔兹曼方法(lattice boltzmann method,LBM)模拟数字岩心模型的流体输运特征，建立微米级渗流模拟，促进微观渗流机理的研究。

现以桂东南地区的花岗岩残积土为例，通过Micro-CT扫描与三维可视化软件Avizo结合，建立孔隙网络模型。目前，此项对接技术主要用于碳酸盐岩、砂岩、页岩、煤、天然气水合物及多孔碳的研究，对于流体在花岗岩残积土的研究极少。运用Avizo相关算法，提取花岗岩残积土的表单元体及孔隙空间结构，并将表单元体划分网格后导入多场耦合软件Comsol进行花岗岩残积土的渗流模拟，通过计算单相流体流经该数字岩心模型的绝对渗透率，与实测值对比，检验该模型准确性、代表性，并研究压实度对花岗岩残积土渗流特性的影响。

1 基于高分辨率CT三维重建

1.1 土样压实度选取及制备

由室内击实试验得到桂东南地区花岗岩残积土的最佳含水率18.9%，最大干密度为1.65 g/cm3[26]，则压实度90%、100%、110%分别对应的干密度为1.485、1.65、1.815 g/cm3；试样按三个干密度值在含水率为18.9%时按压样法制样。然后制作环刀样和CT样分别进行渗透试验和CT扫描试验。CT样为15 mm×15 mm×12 mm的立方体，并用聚乙烯胶盒包装。

1.2 CT扫描

Micro-CT原理是根据花岗岩残积土中不同密度的成分对X射线吸收系数不同，以达到区分孔隙和基质的目的。试验依托三维X射线显微镜Xradia 510 Versa高分辨率CT系统，对桂东南地区不同压实度的花岗岩残积土进行CT扫描，为了减小对岩心的损坏，从15 mm×15 mm×12 mm样品中选取1 010×1 000×1 024体素的部分进行扫描。高分辨率Micro-CT系统及样品如图1所示。得到一组二维切片(1 010张，1 000×1 024像素)，每张切片的灰度值为216，压实度为90%、100%、110%的花岗岩残积土的体素分别为5.81、5.81、6.2 μm。在样品的切片中，黑色表示花岗岩残积土孔隙，灰色表示骨架基质。样品的切片如图2所示。

图1 Micro-CT仪器及土样Fig.1 Micro-CT and samples

1.3 图像处理

1.3.1 滤波处理

CT扫描获得的切片过程难免会产生各种系统噪声，不仅降低图像质量，还直接影响后续图像处理和孔隙结构的定量分析。滤波处理可以剔除信号中特定频率的波段，来提高图像质量。朱洪林[9]、吕邦民[21]使用中值滤波分别对低渗砂岩、多孔碳的灰度图像进行处理，何凯凯使用非局部均值滤波对煤的灰度图像进行处理。针对均值、中值、高斯滤波算法的优缺点，且处理效果侧重点不同，选用单一滤波算法来处理灰度图像通常达不到预期的效果，花岗岩残积土经过中值滤波和非局部均值滤波的处理效果如图2所示，根据处理效果选用非局部均值滤波(non-local mean)对灰度图像进行处理，该滤波结合高斯滤波和均值滤波的特点。花岗岩残积土的灰度图像经过非局部均值滤波处理之后，孔隙和花岗岩残积土骨架基质的边界更容易区分。

1.3.2 阈值分割

阈值分割是重建后的模型能否准确描述实际物理模型的基础，其本质是通过图像的灰度直方图获得分割的阈值。利用孔隙和基质之间灰度值的差异来确定两者的灰度阈值，然后对花岗岩残积土进行三维重建，从而提取出孔隙的相关信息。受CT扫描分辨率及花岗岩残积土中组分复杂的限制，导致孔隙和基质阈值选取更加复杂。阈值选取非常关键，如果选取一个合适的阈值，就能将孔隙准确的分割开来。吕邦民[21]使用OTSU(最大类间方差法 )算法对多孔碳的孔隙与基质进行分割。针对本次试验得到的CT图像，并结合花岗岩残积土孔隙结空间结构特征，进行多种阈值分割方法比选，最终选择OTSU算法。

图2 原始切片及滤波处理Fig.2 Original slice and filter processing

1.3.3 表单元体提取

解决计算机内存容量、运行速度与数字岩心尺寸大小间矛盾是通过选取合适的代表性体积单元(representative elementary volume，REV)。小于REV尺度取得的土体物理特性波动明显，而大于REV尺度取得的土体物理特性趋于稳定。因此，选择大小合适的REV不仅能代表土体的物理特性，而且也能满足计算机的条件。当REV尺寸与孔隙度的变化规律趋于稳定时，REV尺寸即为对应的最小单元体的边长。通过分析REV尺寸与孔隙度的变化规律，发现压实度为90%、100%、110%花岗岩残积土的REV尺寸分别大于220×220×220、200×200×200、200×200×200体素时，土样的孔隙度基本不随单元体尺寸变化，如图3所示。因此，压实度为90%、100%、110%花岗岩残积土选取表单元体尺寸分别为220×220×220、200×200×200、200×200×200体素，则对应的表单元体大小分别为1 278 μm×1 278 μm×1 278 μm、1 162 μm×1 162 μm×1 162 μm、1 240 μm×1 240 μm×1 240 μm。

2 微观孔隙结构模型构建

三维可视化是将花岗岩残积土孔隙与基质的分布结构以更加直观的方式呈现。构建的孔隙网络模型较为真实地还原花岗岩残积土的孔隙分布及连通性。其过程是将分割后的图像进行三维重构。基于选定的阈值和表单元体的尺寸，使用直体积渲染模块，完成花岗岩残积土三维重建，如图4所示。

图3 REV尺寸与孔隙度的关系Fig.3 The relationship between REV size and porosity

图4 花岗岩残积土的三维重构Fig.4 Three-dimensional reconstruction of granite residual soil

3 渗流模拟

3.1 网格剖分、优化

数字岩心模型拥有高质量的四面体网格是利用有限元法进行渗流模拟的重要条件。由于花岗岩残积土孔隙空间结构复杂，直接对重建后的数字岩心模型进行网格划分极其困难，而且导入的模型无法进行渗流模拟。因此，采用Mimics软件，多次修补破面和优化数字岩心曲面模型，其中包括修复尖角、缺口，消除小孔、重合边、交叉、缝隙、倒角等，然后生成高质量的网格。最终将STL文件导入Comsol软件进行渗流模拟。

3.2 控制方程与边界条件

将实际孔隙结构的数字岩心模型作为模拟基础，并展开渗流模拟。其方法有两类：计算流体力学的传统方法(CFD)及格子玻尔兹曼Boltzman方法(LBM)。CFD是对介质模型进行质量、动量、能量守恒方程求解，并对控制方程及模型离散。LBM是一种基于分子运动理论模拟流体流动的方法，流体被看成有质量没体积的微粒，通过模拟微粒在网格中的碰撞和移动，构建简化的运动论模型来反映孔隙空间中流体渗流规律。但LBM方法计算量大、耗时长。因此采用CFD方法中不可压缩Navier-Stokes方程模块来进行孔隙空间结构的流体流动模拟。

(1)

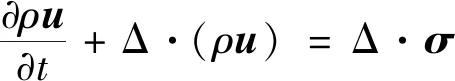
(2)

(3)

式中：ρ为流体密度，kg/m3；t为时间，s；u为流速，m/s；Δ为拉普拉斯算子；e为内能，J；σ为应力张量；q为热通量。

流体属性按常温下水的参数赋值，对花岗岩残积土的模型分别进行X、Y、Z三个方向渗流模拟，设置两个相对立面作为入口与出口边界，4个侧面设为自由滑移壁面，其余壁面视为无滑移壁面。

为了简化模拟与分析过程，作如下假设：①水只在土体孔隙内流动，不会渗透到花岗岩残积土骨架基质；②水为不可压缩牛顿流体，且在孔隙流动的过程中温度保持不变；③水是连续流动的；④水只受到重力和压力的影响。

3.3 绝对渗透率模拟

在Comsol软件数值模拟结果中，对建立好的模型进行计算，对花岗岩残积土在X、Y、Z方向的出口或入口边界水的流动速度进行积分，得到体积流量，再根据达西定律获得其绝对渗透率：

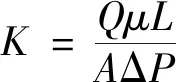
(4)

式(4)中：Q为体积流量，m3/s；A为土体渗流截面积，m2；L为土体渗流长度，m；μ为流体黏度，Pa·s；ΔP为压差，Pa；K为绝对渗透率，m2。

由表1、图5～图7可知，压实度为90%、100%花岗岩残积土在X、Y、Z方向的渗透率差异较小，但压实度为110%花岗岩残积土在3个方向的渗透率差异较大，X方向的渗透率是Z方向的9.27倍，其原因可能是当压实度增加至110%时，分层压实对Z方向上的渗透率影响较大；当压实度增加至110%，花岗岩残积土的渗透率改变2个数量级，其原因可能是当压实度增加至110%时，花岗岩残积土的孔隙形态呈扁平状，孔隙直径减小，土颗粒与其周围溶液的物理化学作用会产生结合水膜，其对土颗粒会产生吸附作用，由于距离不同，故吸附力的强弱会有所不同。距离越近，结合水膜越稳定，在渗透中基本不发生运动。因此，结合水膜的存在会削弱土体的渗透性且从压力云图可以看出压实度为110%花岗岩残积土相对于压实度为90%、100%花岗岩残积土在3个方向的孔隙空间结构发生较大的变化，分布不均匀，进出口面积相差较大。压实度为90%、100%、110%花岗岩残积土在X、Y、Z方向上渗透率模拟值分别是实测渗透率0.89、0.53、1.29、1.74、1.71、0.62、2.02、0.88、0.22倍；其中压实度为90%、100%、110%花岗岩残积土渗透率模拟值平均值分别是实测渗透率0.9、1.35、0.77倍。表明孔隙结构的数字岩心模型具有准确性、代表性。存在差异主要是因为花岗岩残积土在不同方向上存在一定的非均质性且Micro-CT的分辨率有限，无法识别小于分辨率的孔隙，从而会影响渗透率的计算。

表1 花岗岩残积土渗透率模拟结果Table 1 Permeability simulation results of granite residual soil

3.4 压力场分布

通过Comsol后处理得到渗流模拟的速度场分布。虽然X、Y、Z方向的压强差相等，但由于孔隙直径、曲折度、连通性及形状不同，导致3个方向上的压力场分布存在一定的差异，如图5～图7所示。具体表现如下：压力随着水的流动方向逐渐减小,最大压力出现在入口附近狭窄孔隙处；当孔隙通道突然变小时，压力变化快，压力表现为先降低后升高，主要是孔隙通道急剧减小和变弯所致。

图5 压实度90%花岗岩残积土的压力云图Fig.5 Pressure cloud map of 90% compaction granite residual soil

图6 压实度100%花岗岩残积土的压力云图Fig.6 Pressure cloud map of 100% compaction granite residual soil

图7 压实度110%花岗岩残积土的压力云图Fig.7 Pressure cloud map of 110% compaction granite residual soil

3.5 速度场分布

由于连通性及压力的分布导致X、Y、Z方向上的速度场分布存在一定的差异，随着压实度的增加，花岗岩残积土的连通性变差，如图8～图10所示。虽然所有孔隙均已连通，但是有部分孔隙中没有水流过，主要是这部分孔隙小、距入口较远且渗流通道较长。平均速度随着压力的降低而增加，当孔隙通道突然变小时，水的流速突然升高；选取X、Y、Z方向截面的速度图，发现对于单个孔隙而言，沿着孔隙中心向外壁的方向，水的渗流速度逐渐减小。对整个连通孔隙而言，水的最大流动速度在连通性好的中心区域。

如表2、表3所示，在600、800 μm截面上，随着压实度的增加，花岗岩残积土的平均渗流速度和最大流速逐渐减小，仅压实度为100%花岗岩残积土在Y轴800 μm截面的流速反常；随着压实度的增加，在u≥2 m/s、1 m/s≤u＜2 m/s、0.5 m/s＜u＜1 m/s区间花岗岩残积土的流速占比大致呈现逐渐减小，在≤0.5 m/s这个区间花岗岩残积土的流速占比逐渐增大。

图8 压实度90%各截面流体流动速度分布Fig.8 Fluid flow velocity distribution diagram of each section at 90% compaction degree

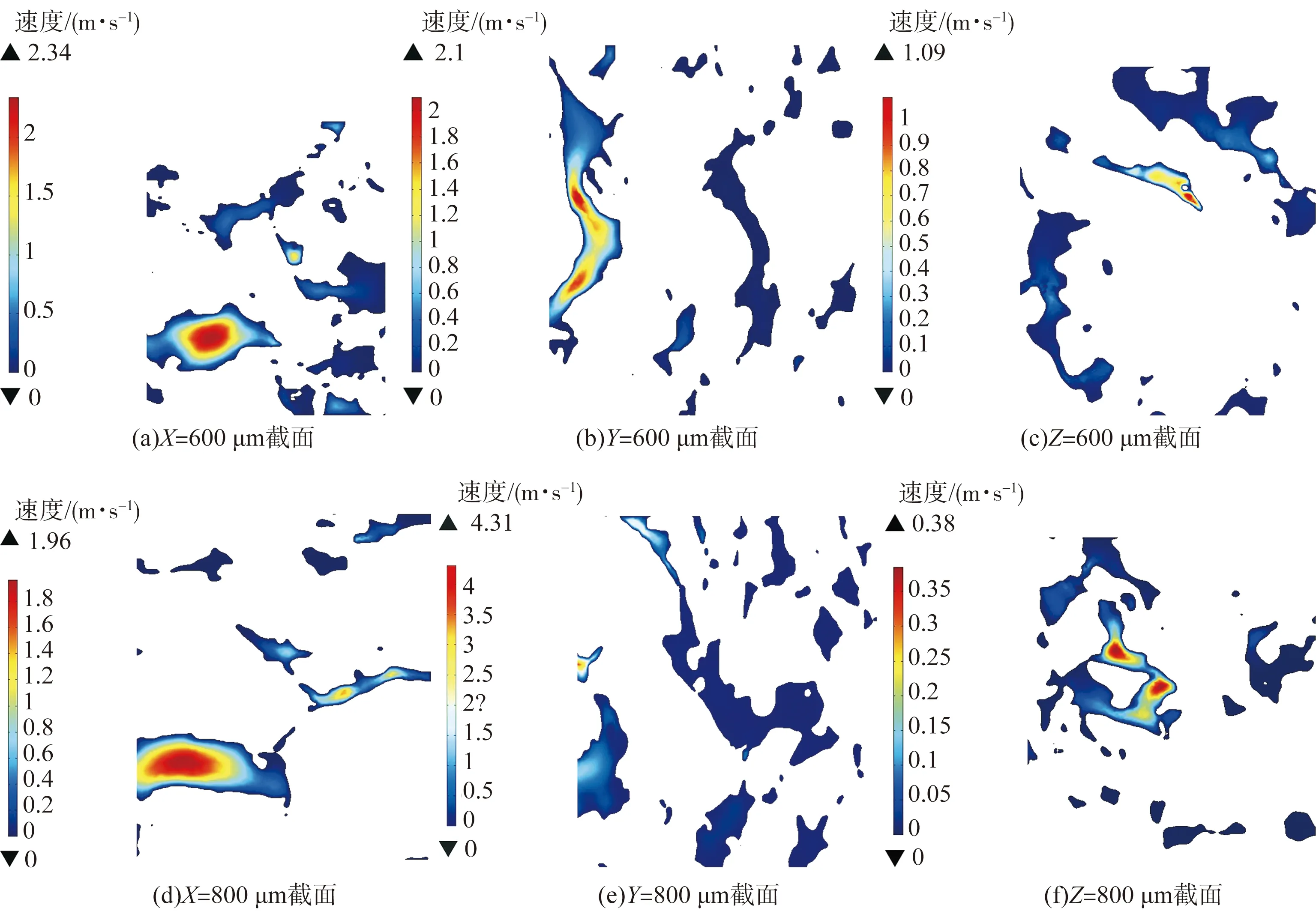
图9 压实度100%各截面流体流动速度分布Fig.9 Fluid flow velocity distribution diagram of each section at 100% compaction degree

图10 压实度110%各截面流体流动速度分布Fig.10 Fluid flow velocity distribution diagram of each section at 110% compaction degree

4 结论

以桂东南地区不同压实度的花岗岩残积土为研究对象，基于CT扫描试验与数字图像处理技术，构建其三维孔隙网络模型，并基于CFD研究水在土体孔隙中的渗流规律，得到以下结论。

(1)CFD作为一种微观渗流模拟方法，不仅可以对不同压实度的花岗岩残积土数字岩心模型的渗流过程进行定量表征，还能够直观描述流体在孔隙内流动的动态过程。且获得花岗岩残积土的绝对渗透率，与实测渗透率进行验证，能为花岗岩残积土渗流模拟提供可靠的模型。此次研究拓宽了CT扫描技术在岩土工程领域的应用。

表3 各方向上截面各速度区间的占比及最大值Table 3 The proportion and maximum value of each velocity section in the cross section in all directions

(2)花岗岩残积土的渗流过程中，在连通性好的孔隙中心区域流速最大，流速沿着孔隙中心向外壁的方向，流体的渗速逐渐减小；在连通性差的孔隙区域流速接近为0。

(3)随着压实程度的增加，在X、Y、Z方向上其截面的孔隙发生较大改变，花岗岩残积土的连通性变差，且截面的平均渗流速度减小，这表明压实度对花岗岩残积土的渗流特性有重要影响。