附加励磁阻尼控制器在某大型火电机组的可行性应用研究
2021-07-29王建军
王建军
(陕西德源府谷能源有限公司,陕西 府谷 719000)
我国能源分布与负荷消纳极不平衡,70%以上的煤炭资源分布在北部和西北部,因此决定了我国远距离大容量的输电方式。随着国民经济和社会的飞速发展,为满足日益增长的电能需求,一方面,通过建设超 /特高压交直流输电线路,提高远距离输电能力;另一方面,通过应用串联补偿技术,提高输电线路的输送容量[1-4]。
特高压直流输电和交流串补输电系统存在导致次同步谐振(Sub-Synchronous Resonance,简称SSR)问题的风险,谐振的发生会危及所在网架结构中火电机组的安全运行。严重时,可能导致发电设备损坏,进而影响送端电网的安全稳定运行[5-6]。因此,准确评估一个火电机组是否存在SSR风险是必要和迫切的,针对SSR风险采取有效的抑制手段也是必不可少的环节。
本文以西北某大型火电机组为例展开研究分析,下图1为A电厂送出系统接线图。图中A电厂一期已投运两台600MW 机组,经A—甲500kV双回串补线路送出。相邻B电厂已投运四台660MW机组,经B—甲500kV三回串补线路送出,甲—乙为四回500kV串补线路。目前A电厂新建二期(两台600MW)机组(图1中蓝色部分)。考虑到串补输电系统可能导致的次同步谐振风险,有必要对A电厂一期、二期机组进行次同步谐振风险研究,以便准确评估A电厂发电机组运行的风险,为后续针对风险采取预防措施做更好准备。
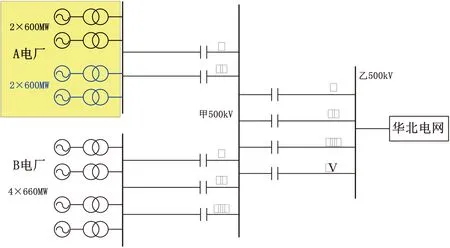
图1 A电厂送出系统接线图Fig.1 Wiring diagram of transmission system in power plant A
1 次同步谐振风险分析
1.1 次同步谐振分析方法
研究串补系统SSR问题常用的方法有:频率扫描法、特征值分析法和时域仿真法。
频率扫描法是通过计算系统阻抗频率特性来初步判断机组是否存在次同步谐振的可能性。对于单机系统,根据串补串联的谐振频率判别协同是否存在SSR的可能性;对于多机系统或有并联的其他线路,通过分析电抗跌落幅值来判断系统是否存在SSR,根据经验,电抗跌落幅值较大时,SSR风险更大。该方法的系统建模详细程度的要求一般低于时域仿真法,采用电网规划数据便可进行仿真计算,是一种经济有效的方法。但由于该方法仅能判断系统发生次同步谐振的风险,而不能分析谐振的严重程度,因此常用频率扫描法对系统各种运行方式进行初步分析,对分析出来确定的次同步谐振问题,再利用其他方法分析其严重程度[7-12]。
特征值法要求的系统信息量大,在应用于大规模电力系统时,容易产生“维数灾”问题,本次研究不采用此方法。
时域仿真法是通过电磁暂态仿真程序,建立包括串补、线路、系统网络、发电机转子轴系模型在内的仿真系统,通过时域求解的方法模拟系统故障或扰动过程,进而求出发电机转子轴系各质块间的扭矩,通过扭矩变化波形判别发电机轴系是否存在SSR问题。时域仿真法也是目前研究次同步谐振 /振荡问题比较精确的方法[13]。
鉴于上述情况,为了更好的评估A电厂机组存在的次同步振荡风险,首先采用频率扫描法对产生次同步谐振问题的运行方式进行初筛,再采用时域仿真法对个别运行方式进行详细分析。使用的时域仿真分析软件为EMTPE和PSCAD。
1.2 频率扫描法分析
A电厂一、二期机组轴系由上海汽轮机厂家生产的汽机转子与上海发电机厂家生产的发电机转子共同构成,机组轴系均由高中压合缸转子、低压缸A转子、低压缸B转子和发电机转子构成,一、二期机组均含有三个模态频率。根据现场实测,机组的模态频率如下表1所示。

表1 机组模态频率Tab.1 Modal frequency of unit
根据频率扫描法,考虑A—甲、B—甲、甲—乙线路及其串补不同投退方式的所有工况组合,考虑A、B电厂1至4台机的不同并网方式组合,去除其中A—甲—乙线路串补全退等工况,对共计75604 种方式进行了研究。研究结果表明:
(1)在所有75604种工况中,有9967种未出现谐振和电抗跌落现象;18253中存在串联谐振频率,53389种存在电抗跌落;也有部分工况既存在串联谐振,也存在电抗跌落;还有部分工况存在多个串联谐振频率和电抗跌落频率。
(2)对上述结果进行统计,串联谐振频率分布在4.5Hz-21.6Hz,电抗跌落超过10%的最低点频率分布在4.5Hz-27.2Hz。上述谐振频率范围与A电厂一期机组轴系模态2、模态3,以及二期机组轴系模态2、模态3存在互补关系,可能会引发次同步谐振。
1.3 时域仿真法分析
在前述系统阻抗频率特性扫描分析结果的基础上,采用时域仿真法,进一步对A电厂送出系统的次同步谐振风险进行研究。
一般的,发电机在满载时机械阻尼最大,空载时机械阻尼最小。此次研究的仿真模型按如下搭建:
(1)B电厂4台660MW机组并网运行。
(2)串补B—甲 I-III 回线全投且均带串补运行。
(3)A电厂一期、二期机组,按照两种最严苛的方式运行:单机空载并网,以及双机一台满发一台空载并网。
按照上述模型进行仿真,仿真中采用的模拟故障类型为:乙站500kV母线发生单相瞬时接地故障扰动。当故障发生时通过观察A电厂一期、二期发电机组的转速差,以及分解到固有模态的发散、收敛情况,从而直观地了解到机组是否会发生次同步谐振。
综合EMTPE和PSCAD时域仿真结果,在全接线、N-1和N-2共3084种系统典型运行方式下,部分工况下A电厂机组在发生系统故障扰动后轴系扭振发散或不收敛,存在次同步谐振风险。
因篇幅有限,本文重点罗列N-2接线方式下个别A电厂机组的次同步振荡风险研究结果。
仿真表明,在甲乙退两回串补或线路,以及A甲、甲乙各退一回串补或线路的运行方式下,A电厂一期、二期机组容易出现不稳定的情况;与一期机组相比,二期机组更不易发生次同步谐振,二期机组在开机台数较少时容易发生不稳定的情况。而在A甲双回线路串补全部退出的典型 N-2 方式下,A电厂一期、二期机组稳定。下表2中选择性列出N-2运行方式的几种机组稳定情况的仿真结果。
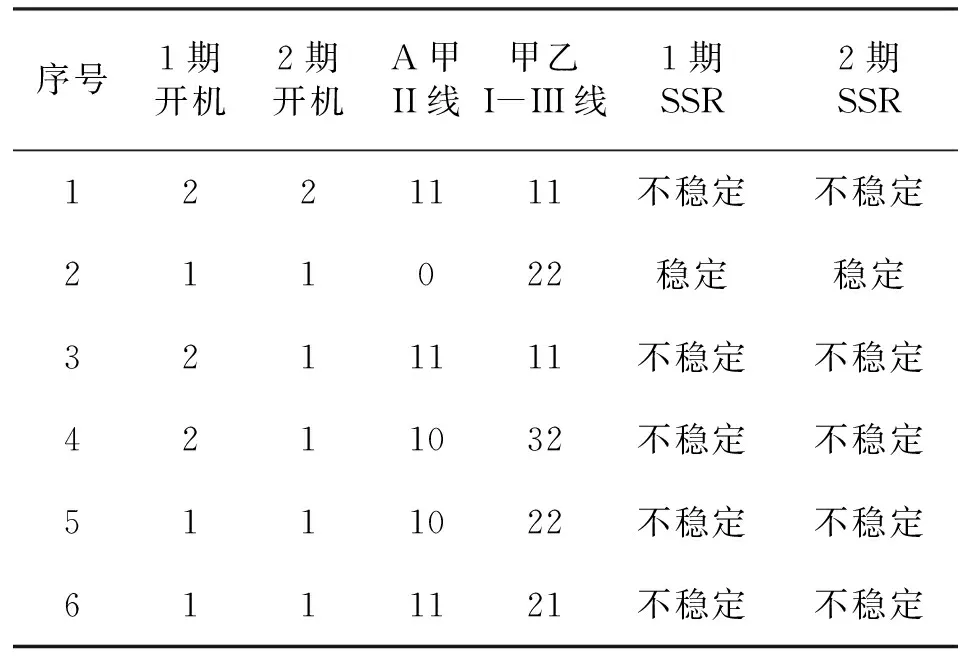
表2 N-2方式下的几种机组不稳定情况Table2 Some units' instability situations of N-2 mode
表2中的几种接线方式下A甲I线和甲乙IV线线路和串补均全投,不再单独罗列。表中线路列中数字的含义为:22表示双线双串补投入,21表示双线单串补投入,0表示线路停运,依次类推。
本文重点以序号6为例进行分析,序号6工况为:
A电厂一期投入一台机组,二期投入一台机组,A甲I线线路和串补均投入,A甲II线线路和串补均投入,甲乙I线线路和串补投入,甲乙II线线路投入、串补退出,甲乙III线线路退出。
下图2为一期机组和二期机组在序号6的工况下的模态曲线图。
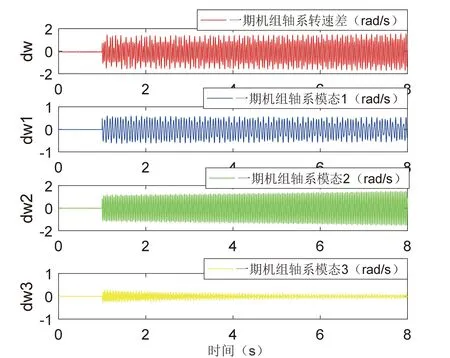
(a)一期机组模态曲线(a)Modal curve of phase I unit
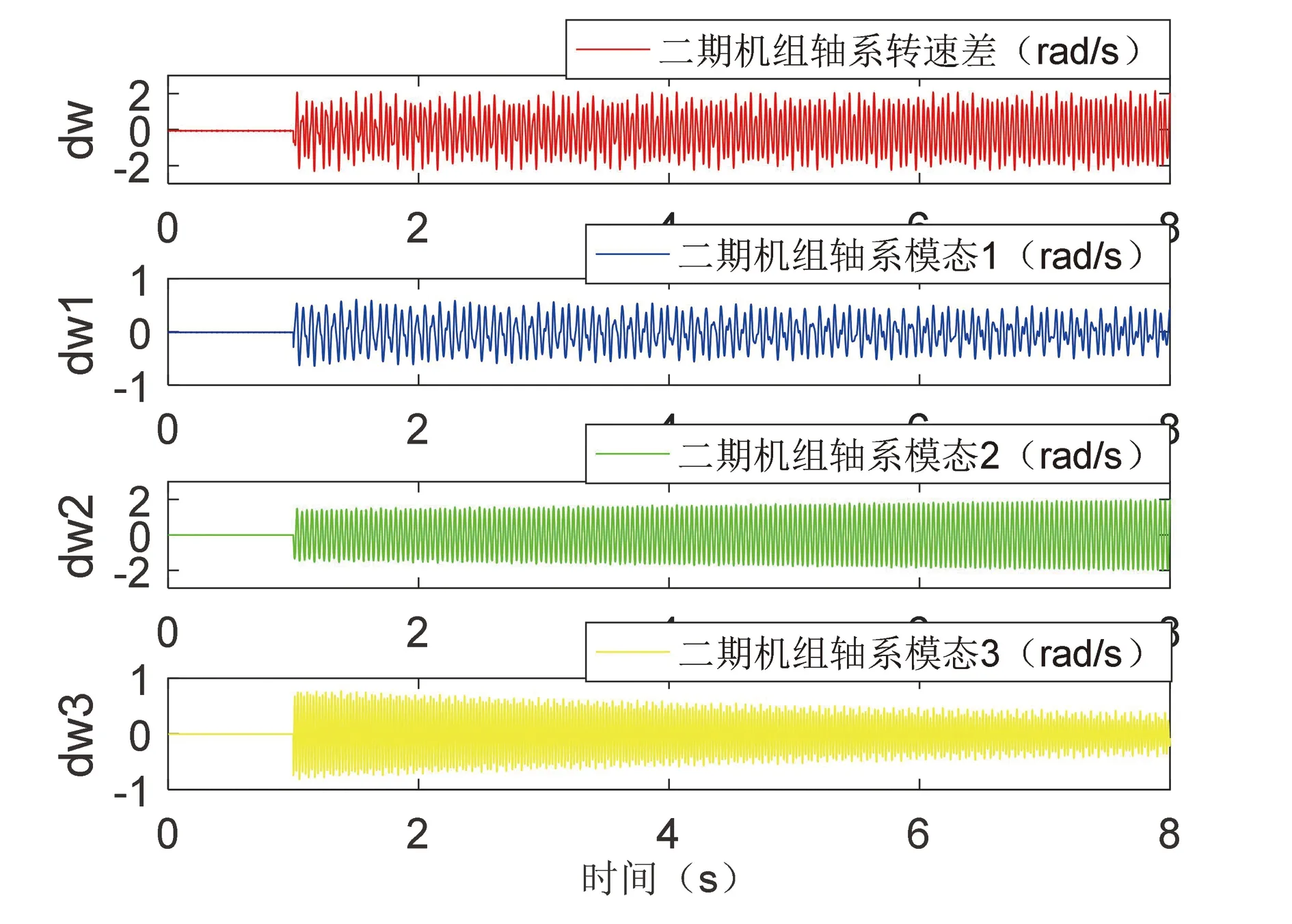
(b)二期机组模态曲线(b)Modal curve of phase II unit图2 序号为6的工况下机组模态曲线图Fig.2 Modal curve of unit under the condition of No. 6
由上图2可看出,根据时域仿真法分析表明:当电网系统以序号6所示的工况运行时,A电厂一期机组模态1呈不收敛趋势、模态2呈发散趋势;二期机组模态2呈发散趋势。此种情况下一期机组和二期机组均属于不稳定运行,均存在次同步谐振风险。
2 抑制措施研究
次同步谐振是汽轮发电机与电网之间不稳定振荡,振荡频率一般高于低频振荡、低于工频,它是一种电力系统局部特殊机电耦合作用引起的振荡。严重的谐振会引发汽轮发电机组轴系不同轴段间产生高幅值扭振,导致轴系危险截面产生疲劳累计,当疲劳累积到一定程度时,可能会造成轴系裂纹、造成机组设备损坏。因此,为了从根本上保障A电厂机组轴系的安全稳定运行,采取次同步谐振抑制措施势在必行,这也是国内大型火电机组常用的轴系保护解决方案之一。
2.1 抑制措施对比
自20世纪70年代以来,国内外学者对次同步谐振问题进行了大量研究,提出了多种次同步谐振抑制方法。目前国内常见的抑制措施有以下四种[14-15]:
(1)静止阻塞滤波器(BF);
(2)静止无功补偿器(SVC)阻尼控制;
(3)附加励磁阻尼控制器(SEDC);
(4)机端次同步谐振阻尼控制(STATCOM)。
其中,附加励磁阻尼控制器(SEDC)需要依托励磁调节系统,其控制输出容易收到励磁强励的顶值影响,且不同现场的励磁厂家不同,现场实施的可行性需提前评估。此特点常常使得SEDC抑制措施现场工程实施环节不作为首选抑制手段。
但与其余三种抑制措施相比,SEDC装置具有以下优点[16-17]:
(1)投资少,设备能耗小。SEDC装置是附加在励磁调节器上的阻尼控制装置,属于二次设备,SEDC装置集成在屏柜中,一台SEDC装置仅用一面占地面积为600mm×800mm的屏柜,相比较其他的一次设备的抑制措施,现场工程实施成本低了很多。
(2)供货周期短。SEDC设备仅为一台装置,装置由机箱和板卡构成,外购设备较少,相比其他抑制措施在生产周期上有极大优势。
(3)参数配置灵活。SEDC装置与发电机组配套使用,不同机组的SEDC装置可根据现场机组参数采用不同的控制参数。
(4)性价比高。SEDC装置可提高机组轴系多个模态阻尼水平,在小扰动情况下可快速阻尼,响应速度快,鲁棒性好。
基于以上优势,采用加装SEDC装置的方式作为A电厂一期、二期机组的次同步谐振抑制措施之一,接下来对SEDC装置在A电厂一期机组上的应用效果进行分析。
2.2 SEDC工作原理
SEDC装置工作的核心数据是机组的转速脉冲信号,现场转速脉冲信号由安装在汽轮机侧的转速传感器采集获得。装置对转速脉冲信号首先进行解调、滤波,解调、滤波后得到与机组轴系模态频率对应的扭振模态信号。分离出各个扭振分量后,装置可对各个扭振模态分量独立进行控制[18-23]。SEDC装置的工作原理如下图3所示。
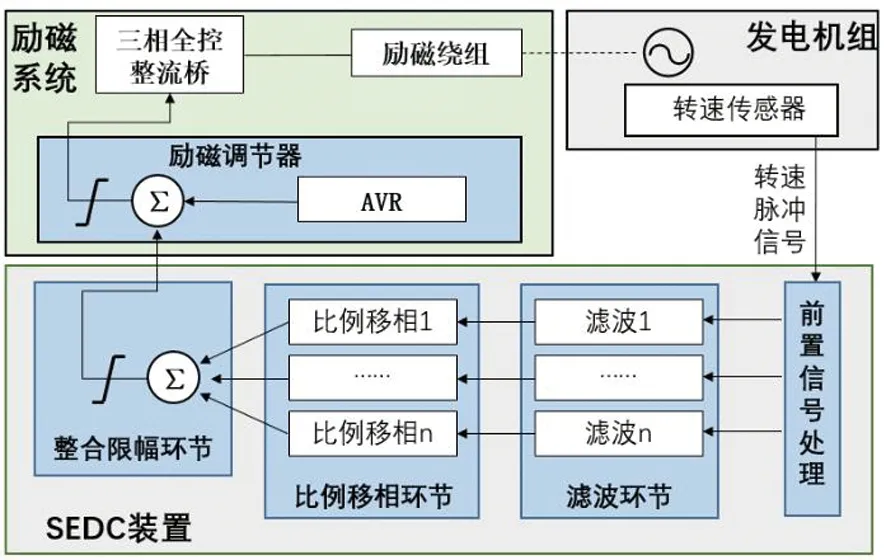
图3 SEDC装置工作原理图Fig.3 Working principle diagram of SEDC device
装置的控制实现按以下四步进行:
(1)对各扭振分量信号进行比例移相处理;
(2)比例移相后对各扭振分量信号分别限幅;
(3)将处理后的各扭振分量信号进行叠加;
(4)对叠加生成的SEDC信号进行输出限值。
经过限值后的综合信号附加在机组的励磁调节器的整流桥臂阀体的触发指令上。当机组产生一定模态频率的SSR振荡时,SEDC装置控制整流桥在励磁绕组上产生次同步频率电压和电流,使得在电磁转矩中包含与模态频率幅值相等、相位相反的次同步频率的阻尼转矩分量,通过这个转矩对次同步谐振起到抑制作用[24-29]。
2.3 定值设计和说明
A电厂一期机组采用的是四方公司生产的SEDC装置,该SEDC装置的核心定值主要包含滤波器环节和比例移相环节参数。根据仿真计算环境,SEDC抑制系统的定值整定过程如下:
(1)根据电厂一期机组的模态频率设置模态滤波器的中心频率;
(2)采用理论分析和PSCAD/EMTPE仿真结合整定SEDC比例移相环节的参数;
(3)根据现场试验环境,对前两步获得的理论参数进行整定。
一期机组SEDC装置的主要定值见下表3。
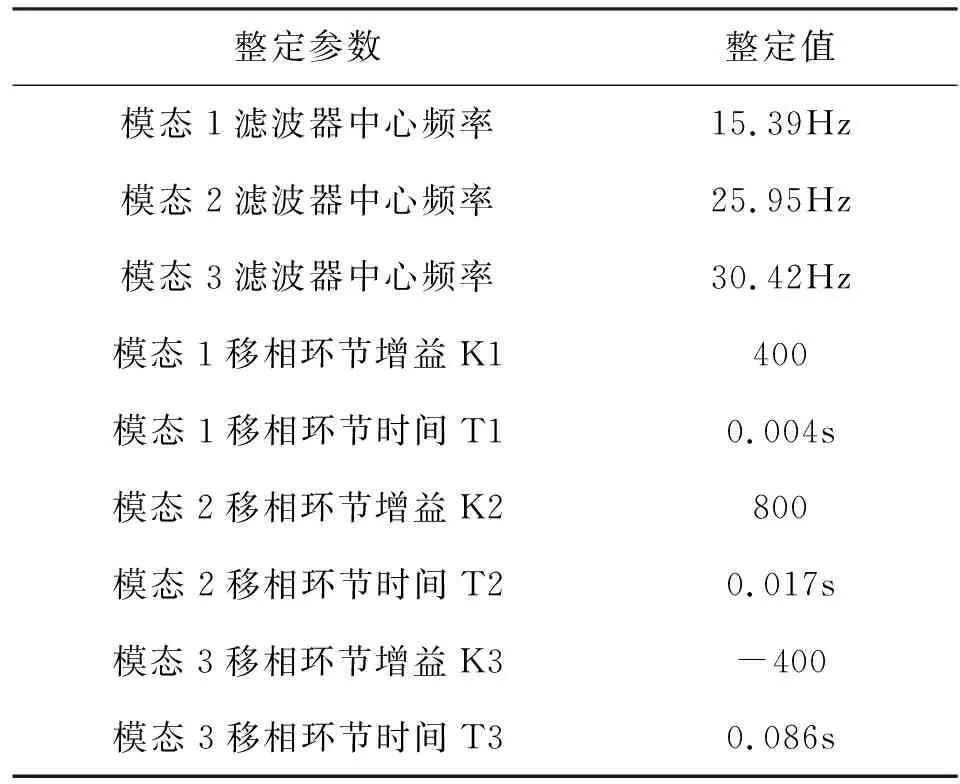
表3 一期机组SEDC抑制装置的主要定值Tab.3 Main settings of SEDC suppression device for phase I unit
3 抑制效果分析
为了验证整定完定值的SEDC装置对机组次同步谐振的抑制效果,本文采用以下两种方式:
(1)使用模态激发装置,对机组轴系模态激发一定的幅值,通过投入和退出SEDC装置进行模态的抑制效果对比。
(2)实际工程现场进行串补投入试验,对比SEDC装置投入和退出时因串补投入激发起的机组模态的幅值和衰减情况。
该电厂中SEDC装置的数学模型如下图所示。
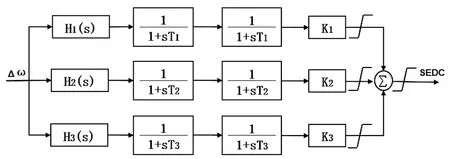
图4 SEDC装置的数学模型Fig.4 Mathematical model of SEDC device
3.1 模态衰减率分析
采用模态激发装置,对A电厂一期机组进行激励试验,激励试验需要注意激发起的机组模态幅值不能太大,以免幅值过大达到机组模态的疲劳累计初始值,对机组轴系危险截面造成疲劳累计,经过前期对电厂机组的阵型及疲劳损伤曲线进行分析,得知三个模态的疲劳累计初值均为0.4rad /s左右。因此本次激励试验通过调整激发装置的控制参数,使得机组的三个模态的幅值均控制在0.15rad /s左右,当激发起来的模态幅值稳定时,投入SEDC装置,记录在投入SEDC装置和未投入SEDC装置时的模态录波,分析并计算三个模态幅值从稳定衰减到0.035rad /s时的模态衰减率,记录结果如下表所示。
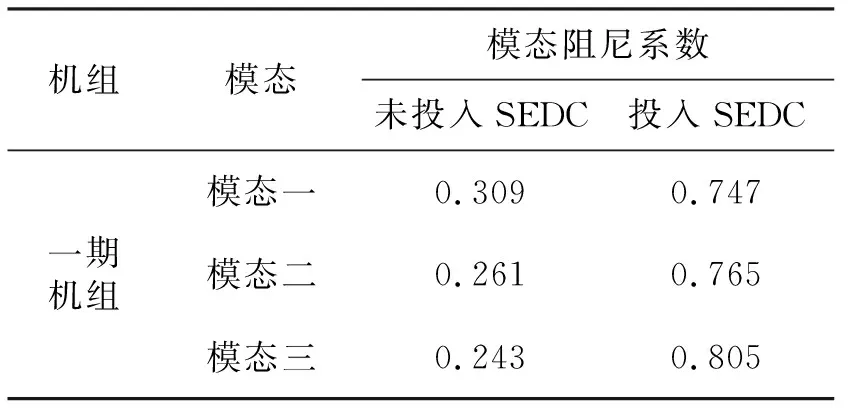
表4 投入、未投入SEDC时模态衰减系数表Tab.4 Modal attenuation coefficient table with and without SEDC
根据上表所示,投入SEDC装置前后一期机组模态阻尼系数有了显著提高,模态一的阻尼系数由未投入SEDC时的0.309提高到了0.747,模态二的阻尼系数由未投入SEDC时的0.261提高到了0.765,模态三的阻尼系数由未投入SEDC时的0.243提高到了0.805。
下图5、图6、图7为一期机组在受到SSR振荡扰动时投入SEDC装置和未投入SEDC装置时的三个模态衰减曲线的对比图,图中红色曲线为投入SEDC装置时机组的模态响应曲线,蓝色曲线为未投入SEDC装置时机组的模态响应曲线。从图中可看出,机组在投入SEDC装置后,受到SSR振荡扰动时,模态幅值比未投入SEDC装置时收敛的更加快速。
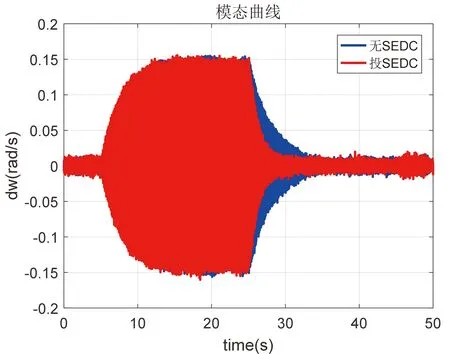
图5 一期机组模态1曲线对比Fig.5 Comparison curves of mode 1 of phase I units
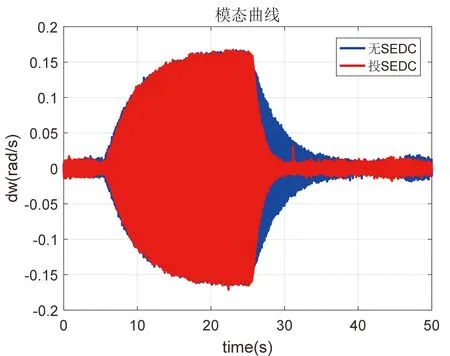
图6 一期机组模态2曲线对比Fig. 6 Comparison curves of mode 2 of phase I units
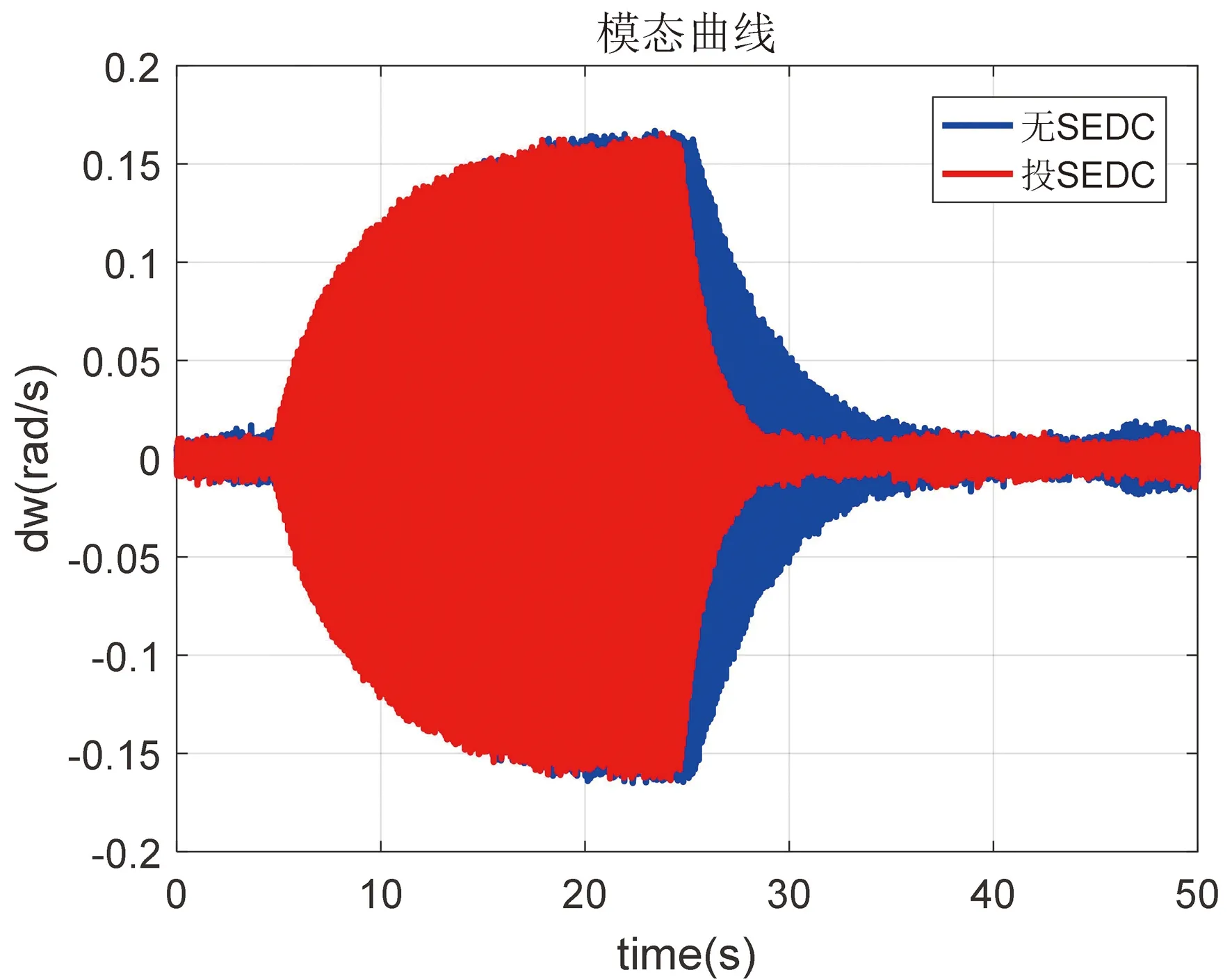
图7 一期机组模态3曲线对比Fig.7 Comparison curves of mode 3 of phase I units
3.2 投串补时装置抑制效果分析
为了进一步验证SEDC装置对机组发生次同步谐振时抑制作用的有效性,下文对线路的串补投入时SEDC装置投入和退出对机组的模态响应情况进行分析。
2020年11月,A电厂一期机组正常稳定运行时,甲乙I线线路的串补进行了投退试验,串补的突然投入会对机组产生一个小的冲击,现场运行的SEDC装置对这一小扰动进行了记录。图8为串补投入时SEDC投入和退出时一期机组的模态曲线对比图。
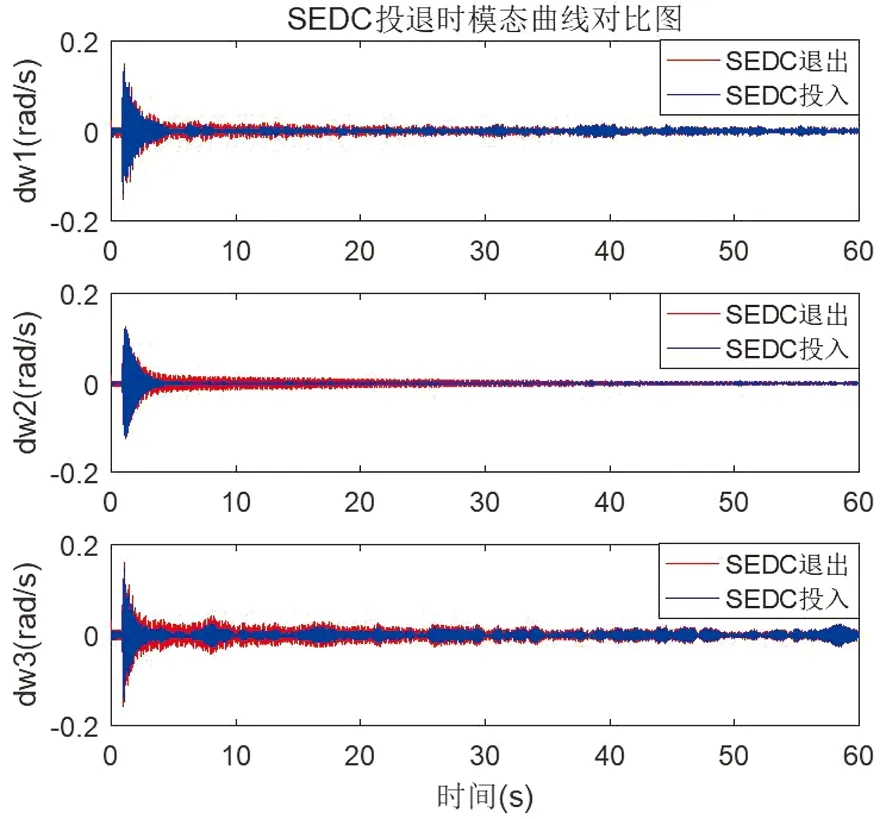
图8 一期机组模态曲线对比图Fig.8 Comparison curves of modal of phase I units
图中红色曲线为SEDC退出时的激发起的模态曲线,蓝色曲线为SEDC投入时激发起的模态曲线。从图中可看出,与SEDC装置退出时相比,当SEDC投入时,机组在串补投入引发模态扰动时一期机组的三个模态幅值能更快速的衰减至较小值。
4 结论
本文以西北某大型火电机组为研究对象,对电网各运行方式进行仿真分析,分析了电网中某些运行方式下该电厂存在的次同步振荡风险,对比现有次同步振荡抑制措施,采用安装SEDC装置作为该电厂的次同步振荡抑制方案之一,分析比较机组在投入SEDC装置和未投入SEDC装置时机组的模态阻尼系数,比较投入SEDC装置和未投入SEDC装置时线路串补投入时机组模态曲线的受扰动情况。
得出当适当的选择SEDC控制回路的增益及其他控制参数时,当系统发生小扰动时,SEDC装置可以有效保证机组在发生次同步谐振后模态幅值快速衰减到较小值的结论。
