基于深度学习的智能电网电力负荷精准预测方法研究
2021-07-29时云洪张龙龙祖良
时云洪,张龙,龙祖良
(中国电建集团贵州电力设计研究院有限公司,贵州 贵阳 550002)
智能电网是国家战略规划,是未来电力系统的发展趋势[1-3]。当前智能电网建设中资源的有效配置是电力工业的首要目标[4]。智能电网包括能源的生产、运输和分配。对未来电力负荷的准确预测是实现这一目标的必要条件,特别是对短期电力负荷的准确预测,因为它允许电力公司为规划和运营做出明智的决策[5],从而节省通常因过载或低负荷成本而浪费的数以百万计的损失,以及不必要的二氧化碳排放[6]。
精确的负荷预测是电力系统一直追求的目标,各种现代的新兴算法、方法运用到负荷预测之中[7]。目前较为流行的预测方法分为物理模型预测和数据驱动预测两类。其中,通过数据驱动的方法因为不需要建立准确的预测对象物理模型而受到广泛关注。最新的研究[8]显示,人工智能与机器学习方法,比如人工神经网络(ANN)、支持向量机(SVM)、决策树等,能够实现较高精度的预测性能。其中,ANN已经成为最常见的预测方法。得益于深度学习的技术革新,深度神经网络已经成为当前研究的热点,如为序列建模和时间序列任务设计的长短期记忆(LSTM)网络,自适应特征提取的卷积神经网络,基于决策树的快速技术算法深度森林等。这些先进的深度学习方法为考虑电力随机波动的不确定性提供了可能。但是,现有的文献资料鲜有考虑电力波动不确定性的研究[9]。
如何利用深度学习将不确定性进行评估以避免由此造成的失误预测仍然是一项挑战。针对此挑战性难题,本文提出了一种新的深度学习方法来解决电网短时电力负荷可靠预测问题,希望能对电力负荷预测研究提供一些有价值的参考。
1 深度学习预测方法
要建立可靠的、完全人工智能的电网系统,准确的电力负荷预测是必要的[10-16]。电力负荷预测如果没有考虑电网系统随机波动的影响是不准确的,会对关键的能源生产和分配决策带来不安全的因素。但是,现有的主流预测模型通常不考虑预测电力负荷的不确定性信息,由此,一旦发生重要波动,其预测结果必然会造成代价高昂、风险巨大的决策失误,影响智能电网系统的可靠性。因此,基于安全、可靠、智慧的角度出发,评估电力负荷的不确定性至关重要的。
本文提出了一种新的卷积神经网络-深度森林预测方法,首先,利用卷积神经网络建立能量预测计算模型,并结合蒙塔卡罗算法量化电力不确定性。其次,将获得的不确定性评估特征以及电力分布特征输入深度森林以准确预测短时电力负荷。该方法的具体工作流程如图1所示:

图1 电力负荷准确预测新方法Fig.1 New method for accurate electric load forecasting
Step 1:从历史数据中整理出充足的相似工作条件下的短时电力负荷数据时间序列,并作为训练样本输入到深度卷积网络。
Step 2:深度卷积网络利用多层卷积和池化,提出隐藏在数据中难以用解析方法刻画或者发现的潜在规律,并以图形数据方式进行储存。
Step 3:利用dropout regularization(丢弃正则化)对深度网络结构进行优化,通过模型参数的不确定评估实现对提取特征不确定的量化,从而为考虑原始数据的不确定性的对预测结果的影响提供可能。
Step 4:最后,采用深度森林对所提取的数据特征进行学习并建立预测模型,实现对电力负荷的准确预测。
1.1 深度卷积网络
深度卷积网络是一种流行的深度学习算法,它可以有效识别复杂矩阵元素之间的空间关系,根据深度卷积网络的理论基础,从而提取关键的数据特征[17]。图2为本文设计的CNN结构,包括一个输入层、两个卷积层(C1和C3)、两个池化层(P2和P4)、一个全连接层(FC5)和一个输出层(Softmax)。
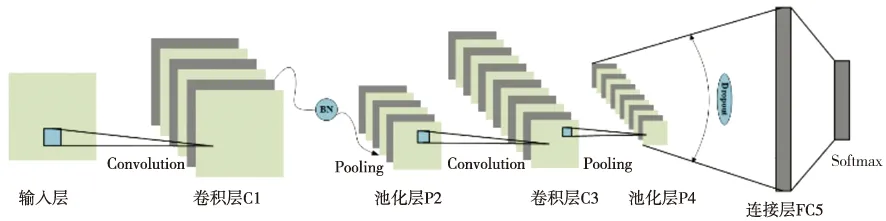
图2 设计的深度卷积网络结构Fig.2 Designed deep convolutional network structure
深度卷积网络使用卷积核提取输入(图像)矩阵的纹理特征,池化层对特征地图进行降采样操作,减少地图维数,获得局部特征。经过两次卷积和池化层后,可以提取出原始图像的基本特征。然后,全连接层(FC5)执行高级推理,将特征映射到不同的类别之中;输出层使用Softmax功能提供特征分类结果。
为了加快深度卷积网络学习过程,减少训练中过度拟合的风险,本文在第一个卷积层和第一池层之间添加了一个基于LeNet-5的批标准化层,同时在第二池层和全连接层之间增加了一个丢弃函数。这样,深度卷积网络的学习效率会更加明显,对敏感特征信息的提取更准确,对后续的预测精度提供良好基础。
1.2 蒙塔卡罗-丢弃正则化
为了度量深度卷积网络模型参数的不确定性,本文采用一种Monte Carlo dropout regularization(蒙塔卡罗-丢弃正则化)算法,利用蒙塔卡罗不确定性估计能力来量化模型参数的不确定性,从而间接地反映出电力负荷数据隐藏的不确定性,使得最后的预测结果准确可靠。
一般地,深度卷积网络可以用函数fw(x)来表示,其中x为网络输入,w为网络权值;经过训练后网络的输出为y=fw(x);对于新样本x*的预测为y*=fw(x*)。为了度量网络的不确定性,蒙塔卡罗-丢弃正则化的计算过程如下:首先利用新数据x*测试训练好的卷积网络,在计算预测的同时采用固定概率p随机丢弃中间层神经元N次,获取一组预测值向量[y*1,y*2,…,y*N]。由此,可以评估网络预测的不确定度为:
(1)
(2)
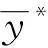
1.3 深度森林
深度森林(gcForest)是随机森林的深度学习衍生物。在随机森林中,首先使用原始数据集x通过Booting策略构造L个子数据集;然后,使用每个子数据集构造一棵决策树,所有子数据集将生成L棵决策树组成的森林;最后,每棵决策树将产生一个输出,而随机森林的最终输出由投票或平均策略决定。深度森林基于随机森林对每棵决策树进行处理,通过计算不同类别在训练数据集中所占的百分比来生成类别的概率分布。因此,深度森林的输出是森林中所有决策树的概率分布的平均值。
深度森林中使用多粒度扫描(MGS)和级联森林实现深度学习。MGS的目的是从输入图像中提取有用的信息:首先,每个灰度图像(M×M matrix;M为图像大小)通过滑动窗口(窗口大小为k)扫描,生成S个子图像矩阵;每个子图像是一个k×k矩阵。如果滑动步长为j,则S= [(M-k)/j+1]2。然后,使用每个子图像同时训练一个完全随机森林和一个随机森林,每个森林的输出向量中有C个元素,对应训练数据集的C类标签的概率。通过连接两个训练森林模型的输出向量,得到每个子图像的2C元素特征向量。因此,对于每一幅灰度图像,两个森林模型都会生成一个维度为S×2C的特征矩阵。最后,连接特征矩阵的每一行,得到一个2×S×C维度概率向量作为每个灰度图像的MGS输出。需要强调的是,可以采用多个滑动窗口对灰度图像进行扫描,从而生成每个灰度图像的输出概率向量。在本研究中,我们使用了一个滑动窗口,灰度图像大小M=28,滑动窗的大小为k=26,滑动步长为j=1,因此,子图像个数S=9。
级联森林是深度森林执行深度学习策略的核心。它接收MGS的概率向量,并输出最终的分类结果。级联森林采用多层结构,每层有两个完全随机森林和两个随机森林。与MGS中的森林相似,级联森林中的每个随机森林模型都输出一个C元素的概率向量,因此,每一层输出的维数为4C。在训练过程中自适应地确定层数,在每一层中使用交叉验证来检查训练性能。
图3描述了梯级森林的训练过程。对于每个灰度图像,第一层的输入为MGS的P(=S×2C)概率元素。然后将第一层的输出(即4C个概率元素)与原P个概率元素连接,形成一个新的向量(即4C+P个概率元素)作为第二层的输入。重复类似的连接,为下面的层生成输入向量,直到最后一层。最后一层的四个森林模型的输出被平均,以产生C类的最终概率。深度森林采取最终概率中的最大值作为结果。由于级联森林的层数是根据训练性能自适应确定的,因此可以针对不同大小的数据集调整模型的复杂度,这比固定层深度神经网络更有效。所以,本文提出的电力负荷预测方法能够灵活多变地处理不同批次数据,且可以自适应数据规模变化,保证稳定可靠的预测精度。
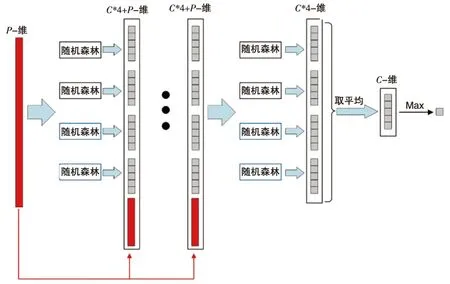
图3 深度森林学习策略Fig.3 Deep forest learning strategy
2 实验数据验证
智能电网核心技术之一是要实现电力供求的优化管理;其中对短时电力负荷的预测尤为重要。为了解决这个问题,本文提出了考虑预测不确定性因素的新型深度学习方法。为了验证该方法的有效性,对某市电网某段时间的电力负荷历史数据进行了分析。所提出的新型深度学习模型由Python IDE (pycharm 2019)执行,所使用的计算机配置为:Intel Core i7-9700K 3.60GHz CPU,32 GB内存,512 GB SSD,1 TB硬盘。
该电网连续记录了2019年完整的电力负荷数据,由于数据量较多,图4仅给出了两天完整的电力负荷历史数据。从数据曲线中可知,原始电力负荷数据展现出明显的波动情况,说明电力负荷在电网运行过程中存在较多不确定性,从而造成数据曲线并未呈现出有用的规律或者趋势。

图4 两天的电力负荷历史数据Fig.4 Electric load curve for 48 hours
进一步,本文对历史数据进行了细节分析,以便提前掌握数据的自身特性,分析电力负荷波动的频繁程度,特别是不同时间段和不同季节对电力负荷波动影响情况,从而为历史数据的分析提供思路。通过仔细分析该历史数据发现,周末(周六和周日)的电力负荷曲线在每个时间点上的分布较为相似,而工作日(周一至周五)由于用电需求复杂多变,导致电力负荷曲线在不同时间点上的分布更加随机,并未出现规律性的概率分布情况,因此对周末的预测难度会比工作日更大;另外,通过分析还发现该数据在夏季的曲线波动情况比其他季节更加频繁,表现出更加复杂的不确定性,从而对电力负荷预测带来了更多不利影响。
为了定量地分析该电网2019年电力曲线在工作日、周末以及夏季的波动情况,对此三个时间段的数据进行了方差计算,结果如表1所示。

表1 电力负荷波动方差Tab. 1 Variance of electric load fluctuation
从表1计算结果可见,该历史数据的电力波动程度一次是周末、工作日、夏季等时间段。可以预见,由于波动带来的不确定性,其预测难度依次为周末、工作日、夏季等时间段。但是,如果能够较好控制电力负荷波动的不确定性,则可以减小不同时间段的预测精度,输出稳定准确的电力负荷预测结果。为了验证这个学术观点,对该历史数据分别进行了不同时间段的预测。
为了检验预测精度,采用了均方根误差(RMSE)和平均绝对百分比误差(MAPE)两个指标。结果如表2-4所示。其中,分别对比了较为流行的LSTM、SVM、随机森林等方法。
表2为对工作日的电力负荷预测结果。分析中选取了电网连续100周工作日(去掉周末)的完整电力负荷数据。从预测结果来看,随机森林和LSTM算法预测结果较为接近,比SVM要准确,但是不如本文方法。这是因为:本文方法对模型进行了不确定性的分析,网络会自适应补偿随机电力波动造成的影响。
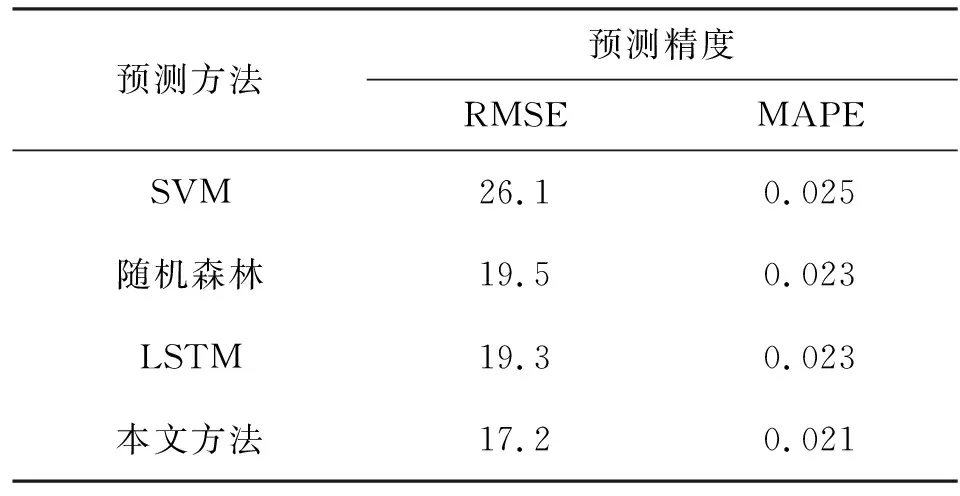
表2 工作日电力负荷预测结果Tab.2 Forecast results of workday electric load
表3为对周末的电力负荷预测结果。分析中选取了电网连续100周周末(去掉工作日)的完整电力负荷数据。从预测结果来看,随机森林和LSTM算法预测结果较为接近,RMSE分别为17.3和17.1,而SVM预测RMSE误差较大,为27.5;本文方法预测效果最好,为14.8。这是因为本文方法能够利用深度森林对样本量的自适应能力,故而该方法会根据实际的样本大小调节森林参数,以实现对不同样本的准确预测。
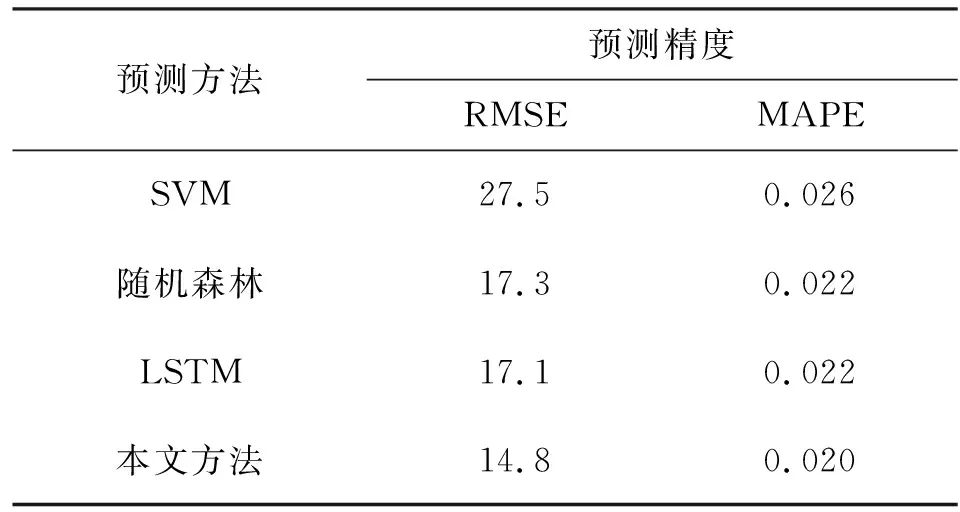
表3 周末电力负荷预测结果Tab.3 Forecast results of weekend electric load
表4专门分析了夏季三个月的电力负荷预测结果。由于夏季用电波动较大,所产生的不确定性也随之增加。从预测结果来看,随机森林和LSTM算法预测RMSE分别为27.8和27.5,SVM预测RMSE误差为35.1;本文方法的预测效果RMSE为18.3。可见电力波动对预测精度的影响较大,但是本文方法仍然能够准确预测电力负荷。由此可见,本文方法是合理有效的电力负荷预测方法。
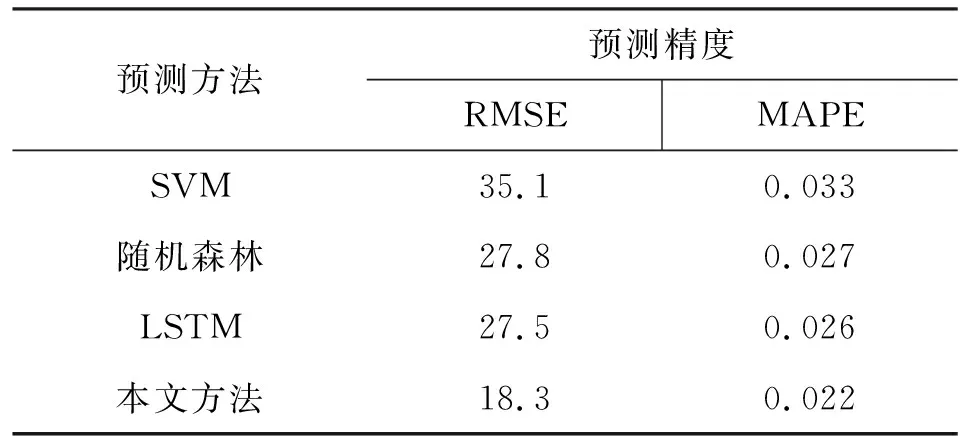
表4 夏季三个月电力负荷预测结果Tab.3 Forecast results of three-month electric load in summer
3 结论
本文针对目前智能电网系统中电力负荷准确预测的关键问题,提出了一种新的深度学习方法,能够解决电力随机波动造成的现有预测方法精度下降的问题。实际电力数据分析结果表明,由于采用了基于丢弃正则化的不确定评估,所提出的深度学习方法能够在电力波动较大情况下准确预测电力负荷,且精度比目前较为流行的方法高。因此,鉴于本文方法的稳定有效性,有望为解决智能电网核心问题提供重要的技术支撑。
