基于NSGA-II 的多机场终端区进场航班排序研究

张艺峰

DOI：10.16660/j.cnki.1674-098X.2101-5640-1042

摘  要：多机场终端区内由于空域结构复杂，机场之间相互影响，空中交通流量大，因而经常会发生航班延误、飞行冲突、机场运行效率糟糕等问题。本文研究多机场终端区的进场航班排序，从航空公司和多机场的利益需求，建立了多目标进场航班排序模型，采用带精英策略的非支配排序遗传算法NSGA-II 进行求解，以成都终端区为例，进行仿真实例验证。结果表明，与经典的先到先服务（FCFS）方法相比较，该方法能有效改善进场航班的延误问题并使多机场能平衡的使用空域资源。

关键词：空中交通管制 多机场终端区 进场排序 多目标优化

中图分类号：V355          文献标识码：A                  文章编号：1674-098X（2021）03（c）-0144-05

Research on Flight Sequencing in Multi-Airport Terminal Area Based on NSGA-II

ZHANG Yifeng

（School of Air Traffic Management， Civil Aviation Flight University of China，  Guanghan， Sichuan Province， 618307 China）

Abstract： Due to the complex airspace structure， the interaction between airports and the large air traffic flow， flight delays， flight conflicts and poor airport operation efficiency often occur in the multi-airport terminal area. This paper studies the incoming flight ranking in the terminal area of multiple airports. According to the benefit requirements of airlines and multiple airports， a multi-objective incoming flight ranking model is established， and the non-dominated ranking genetic algorithm NSGA-II with elite strategy is adopted to solve the model. Taking Chengdu terminal area as an example， the simulation verification is carried out. The results show that， compared with the classical “first come， first served （FCFS）” method， the proposed method can effectively improve the delay problem of incoming flights and make the multi-airport use of airspace resources in a balanced way.

Key Words： Air traffic control; Multi-airport terminal area; Arrival sequencing; Multi-objective optimization

1  研究背景

隨着国内经济逐渐增长和航空运输的发展需求，新建和改建的机场越来越多。根据2019年民航行业发展统计公报统计显示，全国民航运输机场完成旅客吞吐量13.52亿人次，比上年增长6.9%，其中有39个机场达到了旅客吞吐量1000万人次以上，比上年增加了2个[1]。目前国内有双机场的城市有两个，分别是上海、北京。成都天府机场将于2021年建成并运行。珠三角、京津冀以及长三角地区也存在大型联合多机场终端区。多机场终端区内，终端空域耦合关联，各机场相互影响，进离场航班共用多个进离场点、进离场航段，造成飞行冲突和资源竞争。不能合理利用时间和空间资源，导致航班延误、飞行冲突、机场运行效率低下等问题。

关于进场航班的排序问题，国内外学者做了很多的研究。2006年，A.P. Saraf和G.L. Slater提出一种高效的算法，以尾流间隔和航空公司的偏好对飞机进行优先排序[2]。2010年，Andrea DAriano等人研究了繁忙机场下飞机起降排序问题。提出一个分支定界算法在短时间内优化飞机起降序列，使飞机到达和出发时间相对于计划时间的延误最小[3]。2013年，Hancerliogullari等人针对多跑道上的飞机排序问题，采用了贪心启发式和元启发式算法进行求解[4]。2013年，张妍，胡明华，张颖，建立了多机场进场航班排序的0-1整数规划模型[5]。在终端区进场调度问题中，为提高跑道容量，缓解航班延误，2016年，张军峰，王菲，葛腾腾提出了基于分支定界法的多跑道动态排序方法，最小化最后一架航班的着陆时间[6]。2017年，王璐，张小宁，李英，吴辉等人研究了进场交通流在多机场多跑道系统及定位点的排序优化问题，利用Epsilon 约束精确算法对该双目标模型求解[7]。2018年王朋提出了一种混合动态规划算法，该算法参考了CPS算法和滑动窗算法，对进场航班进行分阶段排序，提高了计算速度[8]。2019年，张海潮针对多跑道航班进场排序，提出启发因子和期望启发因子自适应调整的机制[9]。2020年，刘继新，江灏，董欣放，兰思洁，王浩哲采用协同决策（CDM）方法，通过NSGA-II算法解决不同的空中交通密度下的进场航班协同排序[10]。同年，张军峰，游录宝，杨春苇，胡荣等人为同时满足空管、航空公司、机场和旅客的不同需求，基于非支配排序设计了多目标帝国竞争算法[11]，更高效地求得Pareto解[11]。

2  问题描述

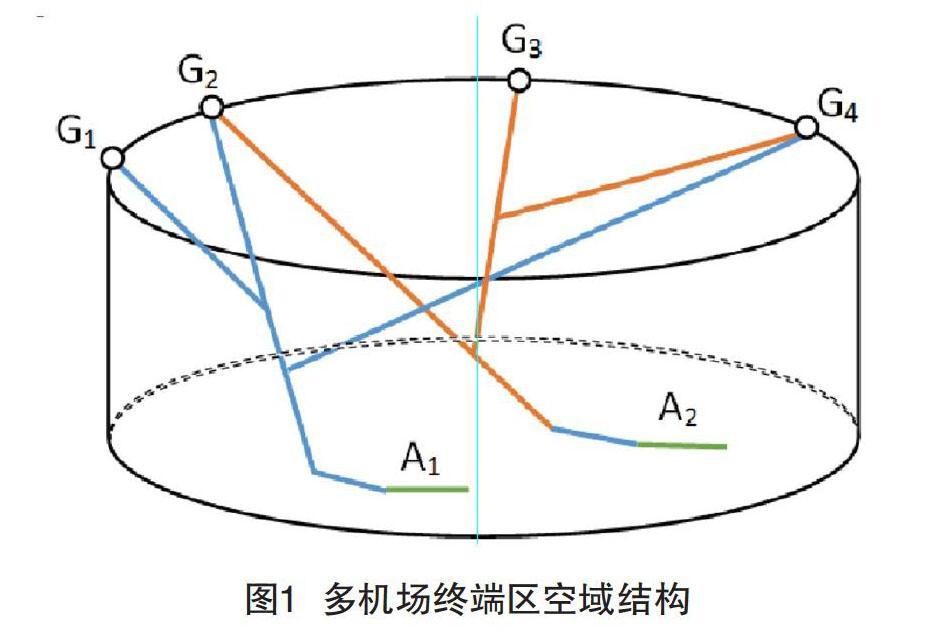
多机场终端区内，空中交通流快速汇聚和发散，空域结构复杂，航线众多。图1为多机场终端区进场航班的空域结构。机场A1和A2的进近航线用蓝色和红色曲线表示，机场跑道系统用绿色直线表示。G1～G4为机场A1和A2的部分进场点，其中G2和G4为机场A1和A2的公共进场点。多机场终端区进场航班排序主要包括进场点排序和机场的跑道着陆排序两部分。所以本文主要考虑的约束限制条件是进场点的管制移交间隔，机场跑道的尾流间隔、同一仪表着陆系统（ILS）航向道和相邻仪表着陆系统航向道雷达间隔等各类间隔约束。

3  模型建立

假设模型变量：i：机场，j：跑道，h：进场航班，u：进场定位点。F：在某段时间所有的进场航班集合;A：终端区内所有机场集合;R：终端区内所有机场的进场跑道集合;G：终端区进场定位点集合;

Ri：Ri为机场i的进场跑道集合，i∈A;

Fij：在机场i的跑道j上降落的进场航班集合，i∈A，j∈Ri，FijF;

αijh：第i个机场第j条跑道的第h架航班到达进场定位点的可行时间窗下限;

βijh：第i个机场第j条跑道的第h架航班到达进场定位点的可行时间窗上限;

eijh：第i个机场第j条跑道的第h架航班预计到达跑道时间;

Sijh：第i个机场第j条跑道的第h架航班实际到达跑道时间;

thu：航班h通过进场定位点u的时间;

：进场定位点u的管制移交间隔标准;

：第i个机场第j条跑道的第h1和第h2架航班之间的尾流间隔标准。

：第i个机场第j条跑道的第h1架航班和第h2架航班之间的同一仪表着陆系统航向道安全间隔标准;

：第i个机场第j1条跑道的第h1架航班和第j2条跑道的第h2架航班之间的相邻仪表着陆系统航向道安全间隔标准，当两条跑道采用独立进近模式时，=0;

3.1 目标函数

（1）航班延误总时间最小。

多机场终端区进场航班在跑道上的降落次序为最终输出队列，因此将以航班实际到达跑道的时间与预计到达时间差值绝对值作为多机场进场航班延误值进行优化，即

（2）各机场平均航班延误偏差最小。

因为多机场终端区内的每个机场有空域资源竞争的关系，所以該模型的优化目标应该使得各机场均衡的使用终端区的空域资源。因此，以各机场平均航班延误最小为优化目标，即

其中，。即δi表示机场i的平均航班延误时间，其中表示机场i的进场航班数量。

3.2 约束条件

（1）管制移交间隔约束。

每架航空器进入终端区进场定位点时，需要必须满足管制移交间隔。

其中，为0-1变量，若航班h1和h2能通过定位点u，且航班h1是航班h2的前机，则为1，否则为0。th1u和th2u是航班h1和h2通过定位点u的时间，若不能通过，则值为0。

（2）尾流间隔约束。

连续降落的前后航空器，后机会受到前机的尾流影响。进场航班必须满足尾流间隔约束。

其中，为0-1变量，若同一机场的同一跑道航班h1先于h2着陆，则为1，否则为0。

（3）多跑道运行间隔。

在多跑道系统下，进场航班应保持同一仪表着陆系统（ILS）航向道和相邻仪表着陆系统（ILS）航向道雷达间隔。

其中，为0-1变量，若同一机场的同一跑道航班h1先于h2着陆，则为1，否则为0。为0-1变量，若第i个机场第j1条跑道的第h1架航班先于第j2条跑道的第h2架航班着陆，则为1，反之为0。

（4）着陆时间窗约束。

为方便对航班进场时间进行编码，我们设置进场航班在机场着陆时应该满足在着陆时间窗内。时间窗下限是根据目前航班的位置和最短距离航线，计算得到的最早着陆时间;时间窗上限是根据航班的载油量和飞行性能等数据，计算得到的最晚着陆时间。

4  算法设计

本文有两个优化目标，即航班延误总时间最小和各机场平均航班延误偏差最小，因此属于NP-Hard组合优化问题。本文采用带精英策略的非支配排序遗传算法NSGA-II 对所建多目标优化模型进行求解。NSGA-II算法可通过快速非支配排序、拥挤距离排序等方法，能使种群具有最优性和多样性，求出使多个目标优化的Pareto解。

4.1 算法流程

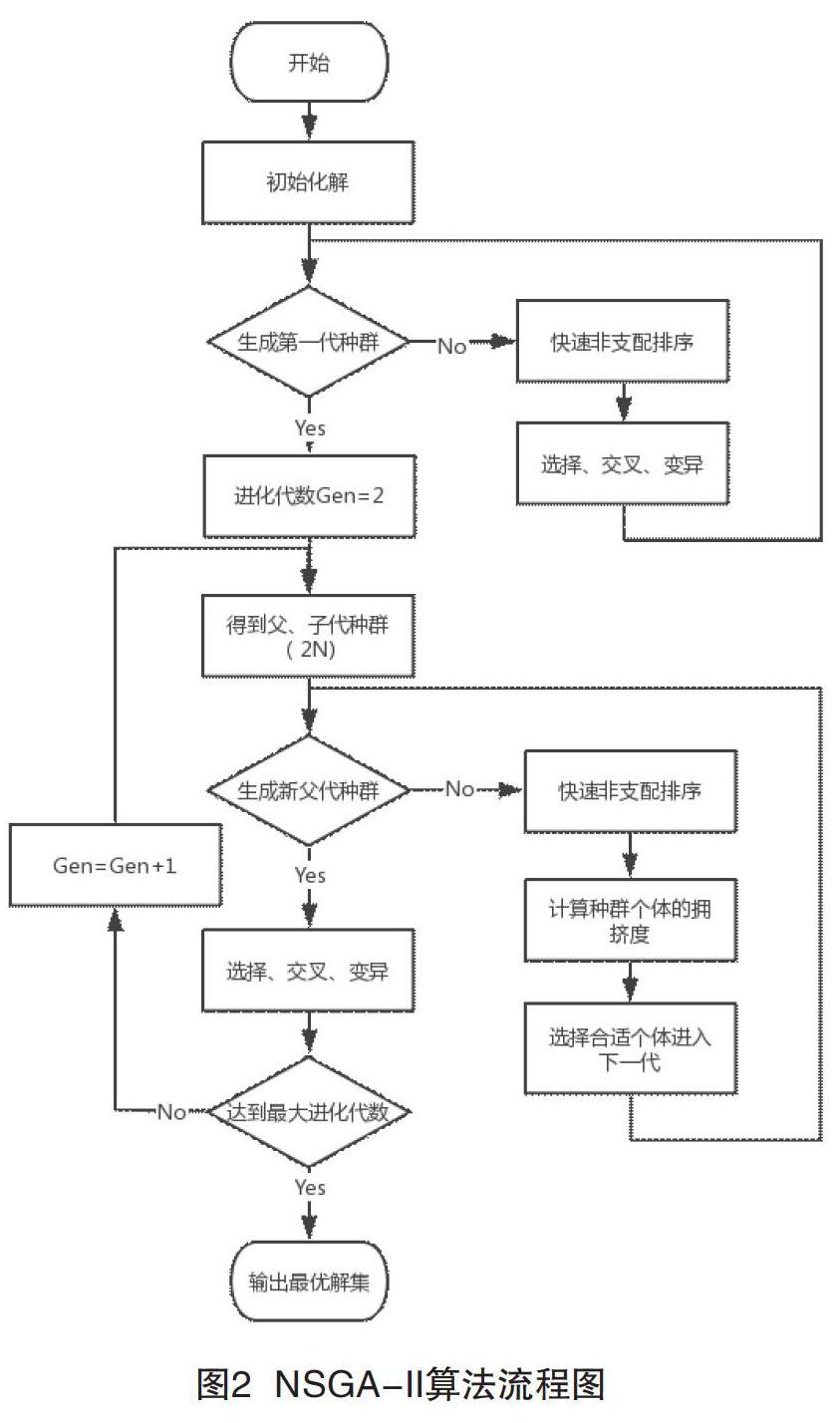
获取多机场终端区进场定位点信息，以及每个机场的跑道数量、运行模式、航班计划数据等信息。根据这些数据获得航班的计划到达跑道时间和着陆时间窗。编码设计所有的进场航班着陆时间窗，随机产生初始父代种群。至此，初始化解完成，下面进行NSGA-II算法，如图2所示。

4.2 算法实现

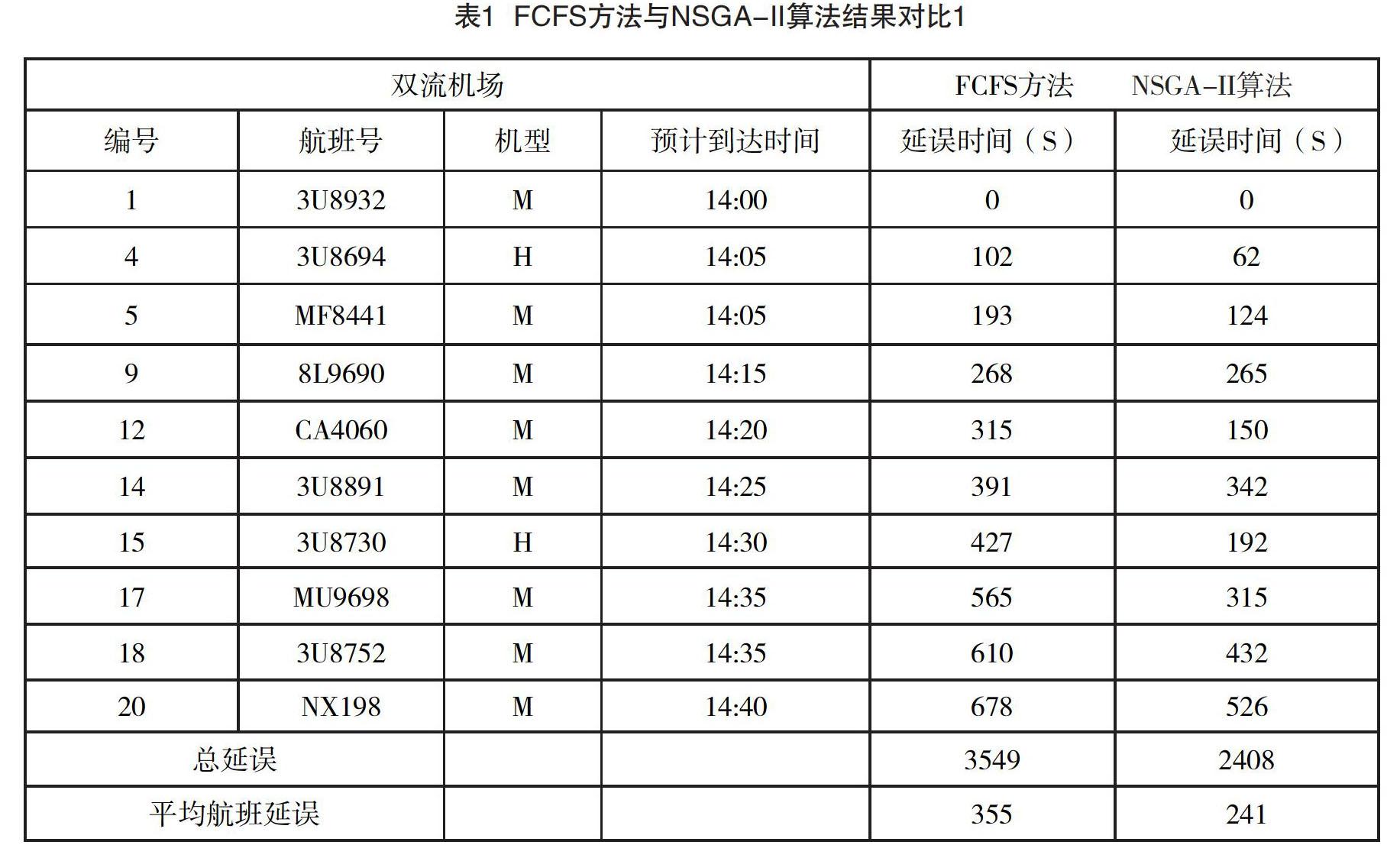
成都多机场终端区，目前有成都双流机场和成都天府机场。因为成都天府机场暂无航班数据，所以随机选择双流机场的进场航班序列插入到天府机场航班序列中。表1和表2分别是成都双流机场和成都天府机场的进场航班在NSGA-II算法优化和FCFS方法对比的结果。进场航班时刻节选自成都双流国际机场某日的流量高峰期。从表1和表2中可以看出，用FCFS方法得出两机场的进场航班总延误是7696s，NSGA-II算法优化下总延误为5231s，延误时间减少了32%。两种算法在两种方法下各个机场的进场航班平均延误差值为60s和41s。因此，该算法对最小化两个目标，即航班延误总时间和各机场平均航班延误偏差，优化效果显著。

5  结语

通过表1和表2的排序结果对比，表明本文提出的基于NSGA-II 的多机场终端区进场航班排序策略是可行的，并且优于经典的先到先服务（FCFS）方法，能明显减少多机场终端区的进场航班延误时间，且基于空域资源的公平性考虑，能减少各个机场的平均延误。

参考文献

[1] 闵梓.民航局公布2019年民航行业发展统计公报[N]. 中国航空报，2020-06-09（007）.

[2] SARAF A P ， SLATER G L . An efficient combinatorial optimization algorithm for optimal scheduling of aircraft arrivals at congested airports[C]// IEEE Aerospace Conference. IEEE， 2006.

[3] D'ARIANO A ， D'URGOLO P ， PACCIARELLI D ， et al. Optimal sequencing of aircrafts take-off and landing at a busy airport[C]// International IEEE Conference on Intelligent Transportation Systems. IEEE， 2010.

[4] HANCERLIOGULLARI， GULSAH， RABADI， GHAITH， AL-SALEM， AMEER H. Greedy algorithms and metaheuristics for a multiple runway combined arrival-departure aircraft sequencing problem[J]. Journal of Air Transport Management， 2013， 32（Complete）：39-48.

[5] 張妍，胡明华，张颖.多机场终端区进场航班排序模型研究[J].航空计算技术，2013，43（3）：20-24.

[6] 张军峰，王菲，葛腾腾.基于分支定界法的进场航空器动态排序与调度[J].系统仿真学报， 2016，28（8）：1909-1914.

[7] 王璐，张小宁，李英，等.多机场终端区进场交通流优化排序方法研究[J].航空计算技术，2017，47（1）：31-34.

[8] 王朋.基于混合动态规划算法的进场航空器优化排序[J].航空计算技术，2018，48（4）：37-40，45.

[9] 张海潮.西安终端区进场航空器排序模型研究[D].德阳：中国民用航空飞行学院，2019.

[10] 刘继新，江灏，董欣放，等.基于空中交通密度的进场航班动态协同排序方法[J].航空学报， 2020，41（7）：285-300.

[11] 张军峰，游录宝，杨春苇，等.基于多目标帝国竞争算法的进场排序与调度[J/OL].航空学报：1-13[2020-08-23].http：//kns.cnki.net/kcms/detail/11.1929.V.20200817.1011.002.html.