压裂直井和水平井的探测区域计算公式

张洪军 ，李新春 ，王瑞刚 ，王小军 ，李二党 ，韩章英

（1.中国石油长庆油田分公司第一采油厂，陕西 延安 716000；2.西安石油大学石油工程学院，陕西 西安 710065）

0 引言

改变井的流量，压力不稳定过程向地层内部推移的距离，即探测半径［1］。探测半径常用于拟时间计算［2］、测试影响范围研究、单井控制储量计算［3］及不稳定产能分析［4-5］等。关于探测半径的研究主要集中在直井，而水平井较少，压裂直井目前未见相关报道。

由于直井井筒具有很好的对称性，探测半径计算公式相对简单，目前已经得到较为完善的探测半径方程［6-11］，然而关于水平井探测半径的研究尚不充分。李传亮等［12］利用压力脉冲波的传播理论，推导了平面单向流的探测距离计算公式，利用该公式可以计算水平井、排状井网或河道条带地层情况下存在平面单向流时的油井探测距离。朱黎鹞等［13］将水平井探测半径的计算问题转为虚拟直井探测半径的计算问题，解决了水平井探测半径的计算难题。陈志明等［14］建立了考虑渗透率动态效应和应力敏感的水平井渗流模型，并采用数值离散法得出了水平井的探测半径。对水平井而言，储层中的流体流动为三维流动，严格来讲，探测半径在3个方向上（垂向、径向垂直水平井方向、径向沿水平井方向）随时间的变化规律是各不相同的。目前的研究成果均只给出了一个综合的探测半径，而它并不能准确反映水平井压力波的传播规律。

直井探测区域为一个标准的圆柱体，用探测半径来描述压力波及范围是合理的。但水平井和压裂直井相对复杂，二者的探测区域并非标准的圆柱体，因此用探测半径来描述压力波及范围还不够准确。

笔者给出了压裂直井和水平井探测区域（包括探测区域外边界和探测区域体积）的精确计算公式，研究了压裂直井和水平井探测区域计算公式的渐近性，并明确了在何种情况下可以采用直井的探测半径公式近似计算这2种井型的无因次探测体积；最后，利用榆林气田一口产气水平井——X井实例验证了本文方法的准确性和可靠性。

1 压裂直井探测区域计算公式

假设在均质无限大地层中，一口压裂直井在0时刻给以瞬时激动产量，且激动前地层中压力均为原始地层压力。储层完全射开，储层上下为不渗透边界，同时假设地层及流体满足：1）储层各向同性、等厚；2）储层中流体及岩石为微可压缩；3）储层中流体满足达西流动；4）压裂裂缝中流量沿裂缝方向均匀分布。

根据以上假设和无因次变量，建立均质储层达西流无因次点源模型［16］：

利用Laplace变换及逆变换对式（1）—（4）进行求解，可得实空间点源压力解。在点源压力解的基础上，沿裂缝方向积分，可得实空间压裂直井的无因次储层压力解：

通过求解压裂直井的储层压力关于时间的导数，导数为 0时可以获得压力波波峰的位置［6，12］。 求式（5）关于时间的导数，令该导数等于0，可得压裂直井探测区域外边界的曲面方程：

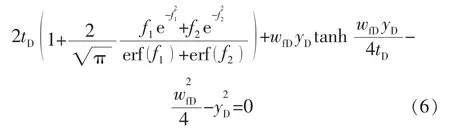
在给定tD和wfD时，可确定压裂直井探测区域的外边界。

在tD→∞时，将式（6）进行渐近展开，可得：

由式（7）可知，当时间较大时，压裂直井探测区域的外边界趋于圆柱面，即。

若取wfD=0，利用积分方法，可得压裂直井无因次探测体积的计算公式：

利用压裂直井的无因次变量定义，将文献［7］的直井探测半径公式进行无因次化，可得：

进而可得对应的无因次探测体积：

相对误差为

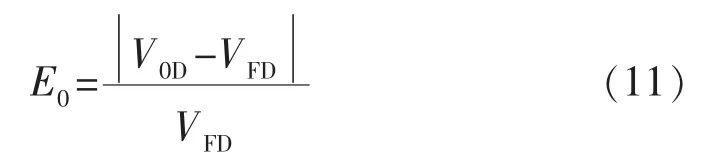
图1给出了wfD=0时压裂直井探测区域外边界曲面随时间的变化规律（裂缝宽度对探测区域外边界曲面的影响非常小，尤其是时间较大时，它几乎没有影响）。当时间增大时，压裂直井探测区域的外边界逐渐趋于圆柱面。

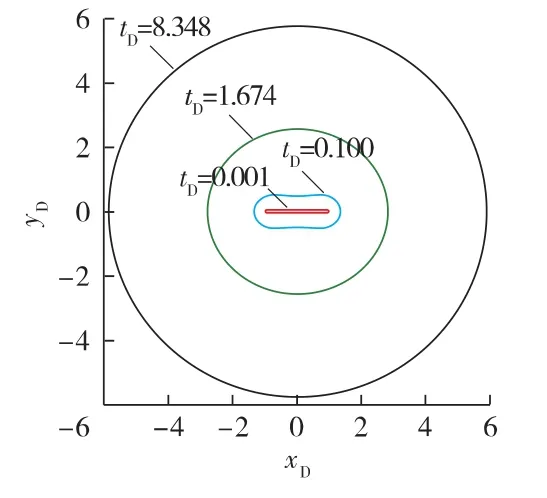
图1 wfD=0时压裂直井探测区域外边界曲面随时间的变化

分别采用文献［7］的直井探测半径公式和本文方法计算压裂直井的无因次探测体积，相对误差结果见表1。由表1可知：随着无因次时间的增大，采用文献［7］的方法和本文方法计算的压裂直井无因次探测体积逐渐接近；特别是当无因次时间分别大于1.674和8.348时，二者的相对误差分别小于5%和1%左右。

表1 压裂直井无因次探测体积的相对误差结果

2 水平井探测区域计算公式

假设在均质无限大地层中，一口水平井在0时刻给以瞬时激动产量，且激动前地层中压力均为原始地层压力。储层上下为不渗透边界，同时假设地层及流体满足：1）储层各向异性（Kr≠Kz），等厚；2）储层中流体及岩石为微可压缩；3）储层中流体满足达西流动；4）水平井中流量沿水平井方向均匀分布。

根据以上假设和无因次变量，建立均质储层达西流无因次点源模型［18-19］：

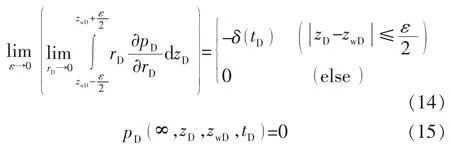
利用Laplace，Fourier有限余弦变换及逆变换对式（12）—（15）进行求解，可得实空间点源压力解［20］。在点源压力解的基础上，沿水平井方向积分，可得实空间水平井的无因次储层压力解：

求式（16）关于时间的导数，令该导数等于0，可得水平井探测区域外边界的曲面方程：

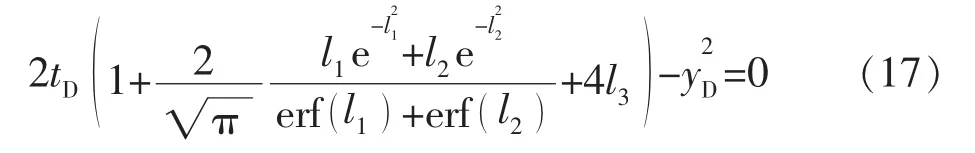
在给定tD，LD，zwD时，可确定水平井探测区域的外边界。

在tD→∞时，将式（17）进行渐近展开，可得：

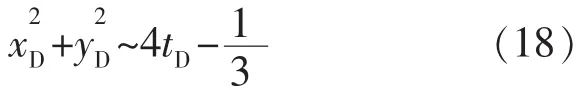
由式（18）可知，当时间较大时，水平井探测区域的外边界趋于圆柱面，即。

利用积分方法，可得水平井无因次探测体积的计算公式：

当 tD≥40/（πLD）2时，l3近似为 0，式（19）可变为

式（20）与压裂直井的无因次探测体积公式形式上完全一致。因此，当 tD≥40/（πLD）2时，水平井的压力传播规律与压裂直井完全类似，可以使用压裂直井的无因次探测体积公式来计算水平井的无因次探测体积。而由表1可知，当无因次时间分别大于1.674和8.348时，可以采用直井的探测半径公式计算压裂直井的无因次探测体积，相对误差分别小于5%和1%左右。因此， 当无因次时间分别大于时，可以采用直井的探测半径公式近似计算水平井的无因次探测体积，此时相对误差分别小于5%和1%左右。

利用水平井的无因次变量定义，将文献［7］的直井探测半径公式、文献［12］及文献［13］的水平井探测半径公式统一进行无因次化，可得：

则无因次探测体积为

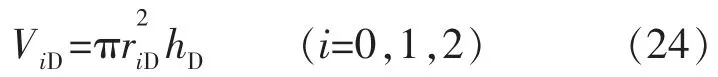
相对误差为

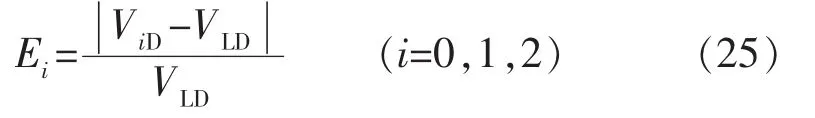
图2给出了4种组合参数对应的水平井探测区域外边界曲面（其中，绿色代表井筒里，红色代表井筒外围地层）。结果表明：储层厚度越大，水平井探测区域外边界曲面触及储层顶底边界的时间越长；垂向渗透率与径向渗透率比值越大，水平井探测区域外边界曲面能够越快地触及顶底边界；水平井垂向相对位置处于储层偏下（偏上）时，水平井探测区域外边界曲面在未触及储层顶底边界时关于xoy，yoz，zox平面对称，而在触及储层顶底边界后仅关于yoz，zox平面对称。

图2 水平井探测区域外边界曲面

分别采用文献［7］的直井探测半径公式、文献［12］及文献［13］的水平井探测半径公式来计算水平井的无因次探测体积，相对误差对比结果如图3所示。可以看出，三者之间没有绝对的优劣之分。总体上来讲，文献［12］的方法不适合无因次时间较大的情况，文献［13］的方法不适合无因次时间较小的情况 （无因次时间必须满足才能使用），文献［7］的方法比较折中。在无因次时间较小的时候，3种方法的计算精度均较差；随着无因次时间的增大，文献［7］和文献［13］的方法计算精度均有提高。

3 实例计算

以榆林气田一口产气水平井——X井为例。其储层及流体物性参数为：储层厚度15 m，孔隙度4.6%，气体黏度 0.022 mPa·s，岩石压缩系数 1.535×10-4MPa-1，气体压缩系数3.24×10-2MPa-1，地层温度45.5℃，初始压力24.5 MPa，天然气相对密度0.6，关井测试前平均产气量40.27×104m3/d。该井的试井解释参数为：井筒储集系数0.191 6 m3/MPa，表皮因子0.13，水平段长度651.6 m，水平井垂向相对位置7.5 m，径向渗透率2.76×10-3μm2，无因次渗透率 0.12。

图4a为试井压力恢复双对数曲线。由图4a可知，水平井理论计算曲线与实测曲线一致，证明了式（16）的准确性，进一步验证了本文方法的可靠性。

图4b为采用部分学者［7，12-13］的探测半径公式和本文方法计算的X井的无因次探测体积随无因次时间变化的双对数曲线。V0D和V1D均与tD呈斜率为1.0的直线，V2D在tD较小时无法计算。而VLD随tD的变化规律大致可以分为3个阶段：1）压力未触及储层顶底边界时（早期径向流），VLD与tD近似呈斜率为1.0的直线；2）压力触及储层顶底边界，但未形成径向流时（中期线性流），受储层顶底边界的影响，VLD的增大速率有所降低，VLD与tD近似呈斜率为0.5的直线；3）压力形成径向流时（晚期径向流），VLD与tD又近似呈斜率为1.0的直线。

图4 X井的试井压力恢复及无因次探测体积变化双对数曲线

本文方法不受时间限制，可以计算水平井任意时刻的无因次探测体积，3个阶段无因次探测体积的变化特征与水平井试井压力恢复双对数曲线特征（早期径向流、中期线性流及晚期径向流）非常吻合。

4 结论

1）本文给出了压裂直井和水平井的探测区域外边界随时间变化的曲面方程。在时间较小时，2种井型探测区域形状较为复杂，但随着时间的增大，2种井型的探测区域外边界逐渐趋于圆柱面。

2）压裂直井裂缝宽度对探测区域的影响非常小，可忽略不计。当无因次时间分别大于1.674和8.348时，可以采用文献［7］的直井探测半径公式近似计算压裂直井的无因次探测体积，此时相对误差分别小于5%和1%左右。

3）当无因次时间大于 40/（πLD）2时，水平井的压力传播规律与压裂直井完全类似。当无因次时间分别大于和时，可以使用直井探测半径公式近似计算水平井的无因次探测体积，此时相对误差分别小于5%和1%左右。

4）本文方法可用于压裂直井和水平井探测区域的精确计算以及气藏瞬态流期间的拟时间计算等，具有一定的理论和实用价值。

5 符号注释

Km为储层渗透率，10-3μm2；h 为储层厚度，m；q 为产量，m3/d；μ 为流体黏度，mPa·s；pi为初始压力，MPa；p 为地层压力，MPa；pf为压裂直井储层压力，MPa；t为时间，h；φ 为储层孔隙度；Ct为综合压缩系数，MPa-1；xf为压裂裂缝半长，m；x为x轴方向距离，m；y为y轴方向距离，m；r为径向距离，m；wf为压裂直井裂缝宽度，m；xw为x轴方向点源位置，m；yw为 y轴方向点源位置，m；δ（x）为狄拉克 δ函数；VFD，VLD分别为采用本文方法计算的压裂直井、水平井的无因次探测体积；xFD为yD=0时x轴正方向上探测区域外边界位置；yFD为xD=0时y轴正方向上探测区域外边界位置；riD，ViD分别为采用相关文献计算的无因次的探测半径、探测体积；Ei为相对误差；Kr，Kz为分别为储层径向、垂向渗透率，10-3μm2；pL为水平井储层压力，MPa；L 为水平段半长，m；z为z轴方向距离，m；zw为水平井垂向相对位置，m；KD为无因次渗透率；ε为数学上极小的正数，无物理意义；xLD为zD=yD=0时x轴正方向上探测区域外边界位置；z0D，z1D分别为xD=yD=0时z轴上探测区域外边界下、上位置；p′LD为无因次水平井储层压力导数；下标 D 表示无因次，i表示分别采用文献［7］、［12］及［13］的计算公式（i=0，1，2）。