一种改进的K-means聚类服装图像分割算法

高樱萍，宋 丹，王雅静，张轩宇

（湖南工程学院计算机与通信学院，湘潭 411104）

0 引言

服装产业是我国主要的经济产业之一，近年来，随着机器学习技术的迅速发展，服装产业也得到了较大的发展，而图像作为服装产业的一种直观、便捷的传输媒介，一直是研究的热点.图像分割作为图像处理的第一步，是计算机视觉的基础，同时也是图像处理中最困难的问题之一.图像分割的好坏对后续的服装分类以及服装检索等都有着重要的影响［1-5］.近年来，图像分割是计算机图像处理与计算机视觉中的一个重要子领域，许多学者对图像分割涉及的各个算法和技术都开展了许多研究［6-14］.图像分割是指根据相似性规则将一幅图像划分为多个子图像区域的过程，旨在分离图像中具有独特性质的区域并提出感兴趣的目标，方便进一步处理.

一直以来，国内外许多学者都对图像分割的方法进行了深入的研究，提出了上千种分割算法，但是这些算法都有一定的不足，至今还没有一种方法能够完全适用于所有图像.目前，彩色图像分割方法主要分为以下几大类：基于阈值的分割方法、基于聚类的分割方法、基于区域的分割方法以及基于特定理论的分割方法.

聚类是模式识别和数据挖掘中的一个重要方向，是一种无监督学习算法，其思想是将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程，该算法的目标就是在相似的基础上收集数据来分类.K-means 算法作为最经典的聚类算法，许多研究者将其用于图像分割领域，但该算法有两个主要的缺点，第一是聚类的数目需要预先设定，第二就是初始聚类中心的选取.

到目前为止，许多学者从不同方面对这两个缺点进行了改进，并取得了一些进展.杨善林［2］等针对如何找到最佳聚类数k的问题，设计了一种空间聚类k值优化算法，基本思想是在其他聚类有效性函数的基础上，构造了距离代价函数，并将距离代价函数作为最佳聚类数的有效性检验函数，这样可以大大缩小最优解的范围，提高算法的效率.霍凤财［4］等提出了一种基于Lab 空间的改进K-means算法来分割彩色图像，将图像从RGB 转换到Lab 空间，并用马氏距离代替欧式距离，最后对图像像素点进行聚类，实现图像分割.Hong Yao［5］等提出了一种K-means 聚类与数学形态学相结合的方法对鱼类图像进行分割，其中聚类的最佳数目由灰度直方图确定，聚类中心数据通过与Otsu 确定的阈值进行比较，对聚类中心数据进行过滤，并利用数学形态学的开闭运算求出鱼体的轮廓.受到文献［4］和文献［5］的启发，本文提出了一种改进的K-means分割算法，利用图像灰度直方图的峰值个数来确定聚类数k的值，并用马氏距离代替传统的欧式距离.实验结果显示，本文提出的算法所确定的k值能够得到较好的分割效果.

1 传统的K-means算法

K-means 算法也称为k均值聚类算法，它采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大.该算法是一种迭代求解的聚类分析算法，基本思想是初始随机给定k个簇中心，按照最邻近原则把待分类样本点分到各个簇，然后按平均法重新计算各个簇的质心，从而确定新的质心，一直迭代，直到簇心的移动距离小于某个给定的值.

K-means 的目的是最小化对数据点和簇中心之间的紧密性进行采样的目标函数，如果用数学表达式表示，计算如下：

假设簇划分为C1，C2，……Ck，则我们的目标是最小化平方误差E：

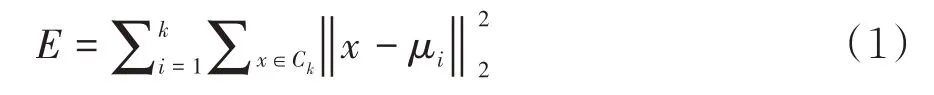
其中μi是簇Ci的均值向量，即质心，表达式为：

影响传统K-means 算法的主要因素就是聚类数k的选择、初始聚类中心的确定以及样本与质心之间的距离.对于彩色图像分割处理来说，聚类的类数往往依赖具体的应用环境和图像分割的目的人所确定，不同的聚类数会产生不同的分割效果.该算法采用目标函数最小化作为聚类结束的条件，且初始聚类中心一般采用随机选择，不同的初始聚类中心可能会导致完全不同的聚类效果.

2 改进的K-means算法

2.1 聚类数目k

针对聚类数目难以确定的问题，本文主要采用灰度直方图进行改进.在K-means 聚类算法中使用直方图的峰值来作为聚类数k，其依据是K-means聚类分割是一种基于图像灰度值和直方图波峰波谷响应图像灰度分布变化的一种聚类过程.图像的灰度直方图描述的是图像中具有该灰度级的像素个数，而直方图的峰值代表这些灰度级的像素规模较大，具有数量优势.因此本文以直方图的峰个数来作为聚类数，即若直方图有k个峰，则聚类数为k.本文先通过式（3）找到直方图所有的波峰，然后根据给定的阈值进行合理选择，若两个相邻峰值之间的距离小于给定的阈值，则丢弃，否则保留.

其中h（i）为第i点的像素值的个数.

本文计算了相邻两个峰谷点的距离，并将所有计算距离的平均值作为阈值，公式如下：

其中dis（i）为相邻峰谷点之间的距离，N为距离的个数.

2.2 马氏距离

传统的K-means 算法中使用的是欧式距离，欧式距离是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离.在二维空间中的欧式距离就是两点之间的距离，公式如下：

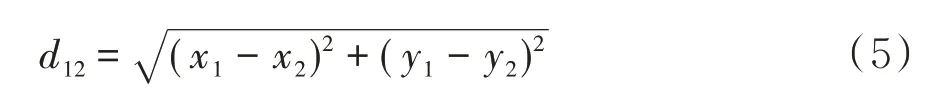
欧式距离由于其计算简单常被用来计算距离测度，但也存在着明显的缺点.这是因为每个坐标对欧式距离的贡献是同等的，当坐标表示测量值时，其带有大小不等的随机波动，在这种情况下，合理的方法是对坐标进行加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离.当各个分量为不同性质的量时，“距离”的大小与指标的单位有关，它将样品的不同属性（即指标或变量）之间的差别同等对待，这一点没有考虑到总体变异对距离远近的影响，有时不能满足实际要求.因此，有学者提出了马氏距离的概念.

马哈拉诺比斯距离（Mahalanobis Distance）简称马氏距离，是由印度统计学家马哈拉诺比斯提出来的，用来表示数据的协方差距离，是一种有效的计算两个未知样本集的相似度的方法.马氏距离的目的就是将方差归一化，使得特征之间的关系更加符合实际情况，它与欧式距离主要的区别就是它能考虑到各种特性之间的关系.在公式计算上，马氏距离采用的是协方差矩阵，协方差矩阵能够衡量多个变量之间的相关性，除此之外，还可以实现数据完全去相关，即在图像处理中弱化甚至消除图像中的相关性.

对于一个均值为μ=(μ1,μ2,μ3,…,μp)T，协方差矩阵为∑的多变量x=(x1,x2,x3,…,xp)T，其马氏距离为：

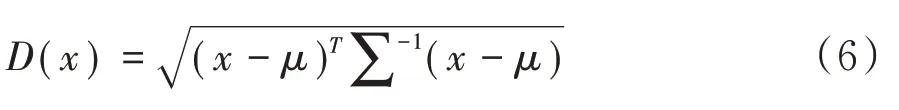
当上式中的协方差矩阵∑-1是单位阵时，此时马氏距离等同于欧式距离，因此欧式距离可以看作是一种特殊的马氏距离.

对于根据距离做判别的问题来说，马氏距离比欧式距离更适合做判别.因为它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关.由标准化数据和中心化数据（即原始数据与均值之差）计算出的两点之间的马氏距离是相同的.

2.3 改进的K-means算法

本文主要针对K-means 算法中聚类数目k难以确定的问题进行了改进，并使用马氏距离代替欧式距离，来得到更好的分割效果.首先读取图像并将图像转换为double 型，通过分析该图像的直方图得到聚类的数目k，然后根据像素间的相似性进行聚类，通过多次迭代更新聚类中心的位置，直到目标函数收敛，最后输出分割后的结果.

该算法的主要步骤如下：

step1：首先求出输入图像的灰度直方图的峰值，确定k值，即将数据集经过聚类得到k个集合

step2：随机选择k个数据点作为质心.

step3：对该图像中每一个点，计算其与每一个质心的马氏距离，离哪个质心近，就划分到那个质心所属的集合.

step4：把所有数据归好集合后，一共有k个集合.然后重新计算每个集合的质心.

step5：如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），此时认为聚类已经达到期望的结果，算法终止.

step6：如果新质心和原质心距离变化很大，需要迭代step3～step5 步骤.

算法的流程图如图1 所示.

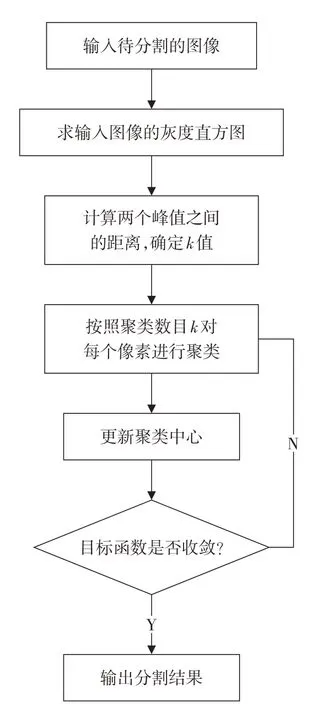
图1 改进K-means算法流程图

3 实验结果

为了验证本文提出的算法，实验在windows10操作系统，软件Matlab R2017a 中进行，并选取不同的k值进行对比，以此验证本文算法的有效性.从服装图像数据库中收集了126 张服装图片进行实验，选取的图像的背景均为白色，其中的一部分图像如图2 所示.

图2 部分实验图片集

本文首先将输入的服装图像转化为灰度图像并求出其灰度直方图，然后对灰度直方图进行运算处理得到符合条件的峰值点，用红色的“*”标出.同时，为了对比不同聚类数k对图像分割结果的影响，本文还分别选取了三个不同的k值，并在同一情况下对同一幅图像进行分割，得到对比图.图3（a）、图3（b）、图3（c）、图3（d）为测试实验中的四张图片，代表了吊带连衣裙、背心套装、上衣、无袖连衣裙，

图3 示例图片（吊带连衣裙、背心套装、上衣、无袖连衣裙）

图4（a）、图4（b）、图4（c）、图4（d）是每张图片对应的灰度直方图.

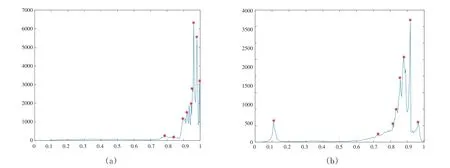
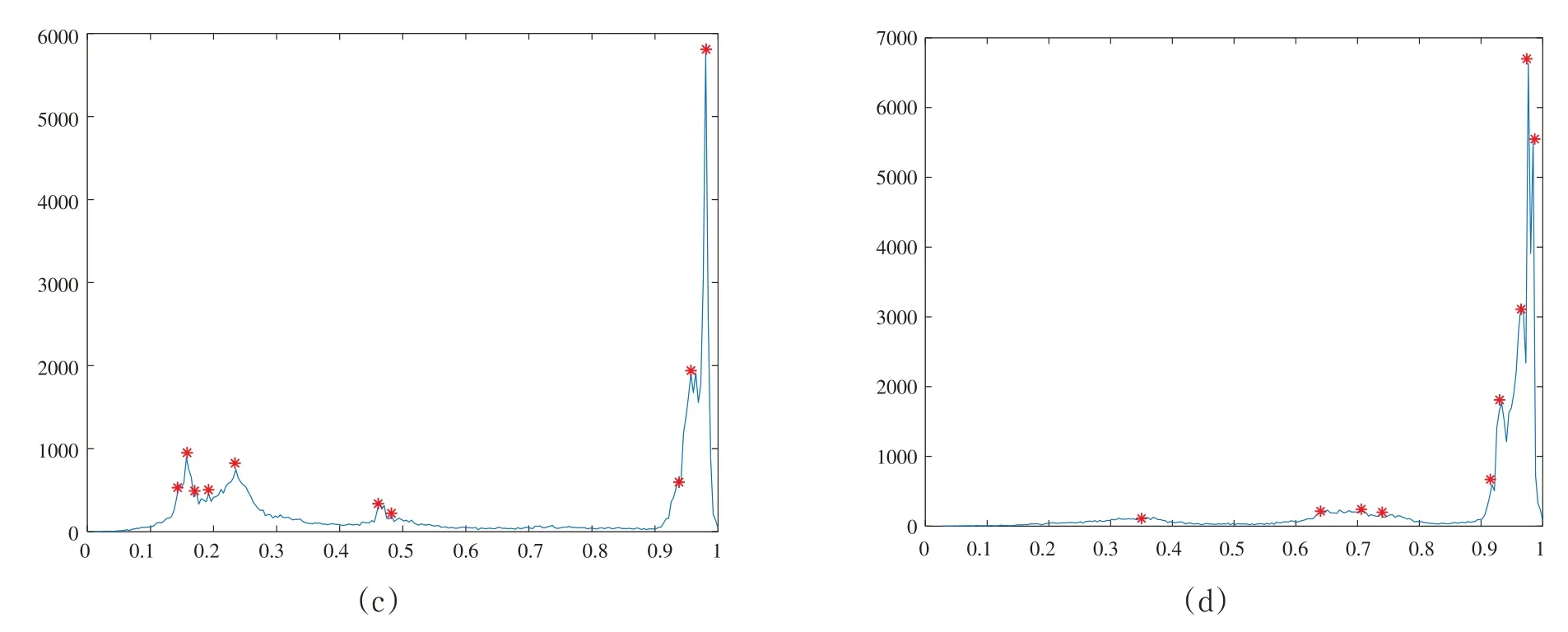
图4 待分割图像的灰度直方图

根据灰度直方图中“*”的数量，我们可以得知图3 中四张图片的聚类数分别为9、8、10 和9.

图5 不同k值分割效果（其中带*号的k值是通过直方图的峰值数得到的）

通过上面的对比图看出，对于图3 中的四张图片，聚类数k分别为9、8、10 以及9 时得到的分割效果最好.实验结果表明，使用本文所提出的方法得出的聚类数k能够得到更好的分割效果.

对所有实验图片的聚类数k进行统计与分析后发现，本文所提出的方法对于浅色的连衣裙类的服装图像有较好的分割效果，且该类图像的聚类数一般在9～12 之间时分割的效果最好.同时，在实验过程中发现，模特的肤色以及发色等都会对分割结果产生一定的影响.

表1 聚类数k的取值

4 结论

K-means 聚类算法作为一种简单有效的算法，在图像分割中有着广泛的应用，但传统的K-means算法的聚类数k难以确定，而且用于计算相似度的欧式距离也有一定的不足，导致图像分割的结果往往不如人意.本文在传统的K-means 算法的基础上，提出了一种改进的K-means 算法，通过分析待分割图像的灰度直方图确定聚类数k，并在进行相似度计算时，采用马氏距离代替欧式距离，实验结果表明，本文提出的算法与传统的算法相比能够得到更好的分割效果.