基于精英反向学习粒子群算法的光伏电池参数辨识
2021-07-28林国汉
张 枭,林国汉,2,胡 慧,2
(1.湖南工程学院电气与信息工程学院,湘潭 411104;2.湖南省风电装备与电能变换协同创新中心,湘潭 411104)
0 引言
为应对气候变化、全球变暖、传统化石燃料耗尽等问题,可再生能源的利用越来越受到重视.太阳能是取之不尽、用之不竭的清洁能源,太阳能通过光伏发电系统将光能转化为电能.然而光伏发电系统通常在恶劣的室外环境下运行,容易退化,严重影响太阳能的利用效率.因此,为了对光伏发电系统进行控制和优化,根据可测的电流-电压(IV)数据,建立精确的光伏电池数学模型,对光伏发电系统实际运行状态进行评估至关重要.目前,最常见和被广泛采用的光伏电池模型是单二极管模型和双二极管模型[1].光伏电池模型的精度主要取决于模型参数,然而,厂家提供的数据手册没有给出模型参数值,且参数会因光伏电池老化、故障和运行环境而改变.因此,在光伏发电系统的仿真、评估和控制中,对参数的准确辨识是必不可少的.目前,光伏电池模型参数辨识的方法主要有参数近似求解法和智能优化算法估计法.利用光伏电池电流-电压模型的特性方程,通过数学分析方法(如微分求导、模型简化)进行处理,可求得模型参数的近似值,但由于光伏电池模型的I-V 特性方程是一个含有超越函数的非线性方程,其具体参数无法直接通过简单计算求得[2].智能优化算法受到各种自然现象的启发,被广泛应用于光伏电池模型的参数辨识中[3-4].在文献[5]中,提出了一种基于惩罚策略的差分进化方法用以辨识不同环境条件下太阳能光伏电池组件的参数.文献[6]通过引入新的比例因子和交叉率,提出了一种改进自适应差分进化算法对电池参数进行估计.文献[7]提出一种用于混沌鲸鱼优化太阳能电池参数估计算法,该方法的主要优点是利用混沌映射来计算和自动调整优化算法的内部参数.文献[8]在蚁狮优化算法中采用混沌序列进行初始化,融入粒子群算法对光伏电池参数进行辨识.文献[9]将自适应缩放因子和交叉变异概率融入差分进化算法,并将改进算法应用于光伏组件模型参数估计,算法取得了较好的辨识精度.
相对于参数近似求解法,智能优化算法在参数辨识精度方面有一定优势,但大部分传统优化算法具有易早熟而陷入局部最优解等缺点,导致参数估计准确性较差.
针对传统智能算法应用于光伏电池参数辨识时存在准确性低、易陷入早熟的问题,提出了一种精英反向学习粒子群(EOPSO)算法.在所提算法中,依据概率,对当前种群中的精英个体进行反向学习,生成一个反向精英种群,然后将生成的反向精英种群与当前种群进行竞争,同时,当算法停滞时,对反向精英种群和当前种群的最优粒子进行柯西变异,增强算法的局部开采能力,使最优粒子逃离局部最优区域.将改进算法应用于光伏电池参数辨识,实验结果表明,改进的粒子群算法在辨识精度和可靠性方面表现出良好的性能.
1 光伏组件数学模型
1.1 单二极管光伏电池模型
近年来,学者提出了不同的等效电路模型来描述光伏电池的电特性.应用最广泛的模型是单二极管模型和双二极管模型,这两种模型也是建立光伏组件数学模型的基础[10].
由于单二极管模型能够方便、准确地描述光伏电池的静态I-V 特性而得到了广泛应用,本文主要对此模型参数进行辨识,其等效电路模型如图1 所示.
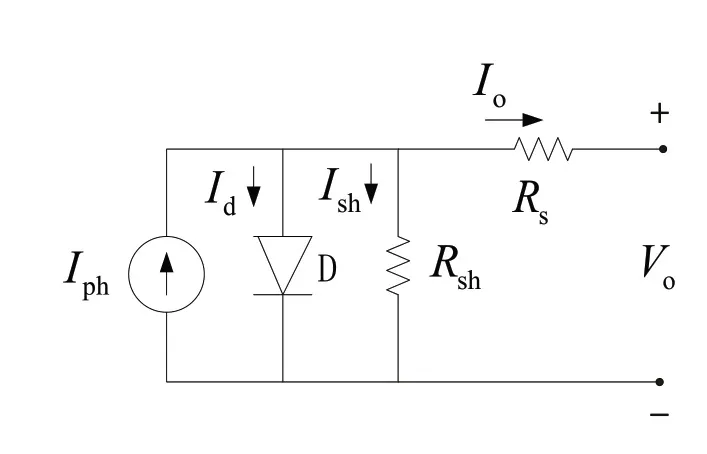
图1 单二极管光伏电池模型
从图1 可以看出,单二极管光伏电池模型由光生电流源Iph、并联二极管D、串联电阻Rs和并联电阻Rsh组成[12],根据基尔霍夫电流定律,光伏电池的输出电流Io可表示为:

其中,Iph为光生电流,Ish为并联电阻电流,Id是并联二极管电流,根据肖克利方程和基尔霍夫定律,可以推导出Id和Ish的表达式为:
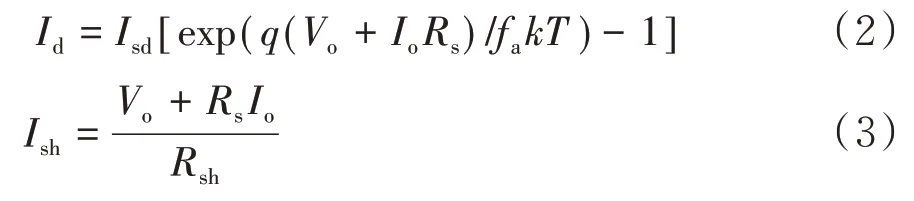
其中Isd为二极管反向饱和电流,Vo为输出电压,fa是二极管理想因子,k是波兹曼常数(1.3806503×10-23J/K),q是电子电荷(1.60217646×10-19C),T为光伏电池绝对温度.
结合式(1)~式(3),单二极管光伏电池模型的I-V 关系为:
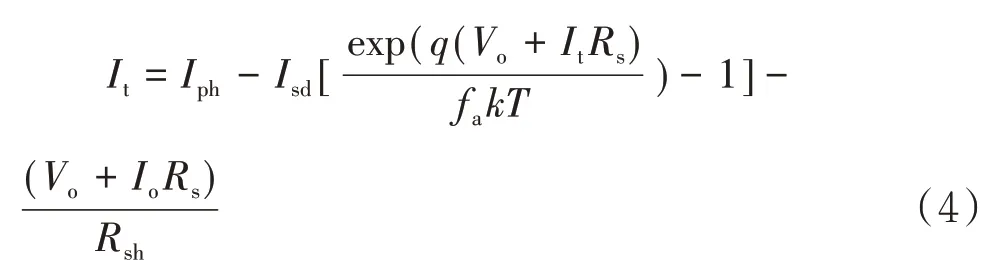
由式(4)可知,单二极管光伏电池模型中未知参数有5 个,分别是Iph、Isd、fa、Rs和Rsh.
1.2 光伏组件模型
在实际应用中,单个光伏电池不能直接用作电源,光伏组件由若干个光伏电池串联或并联而成,以提高其输出电压和输出电流,光伏组件等效电路如图2 所示.
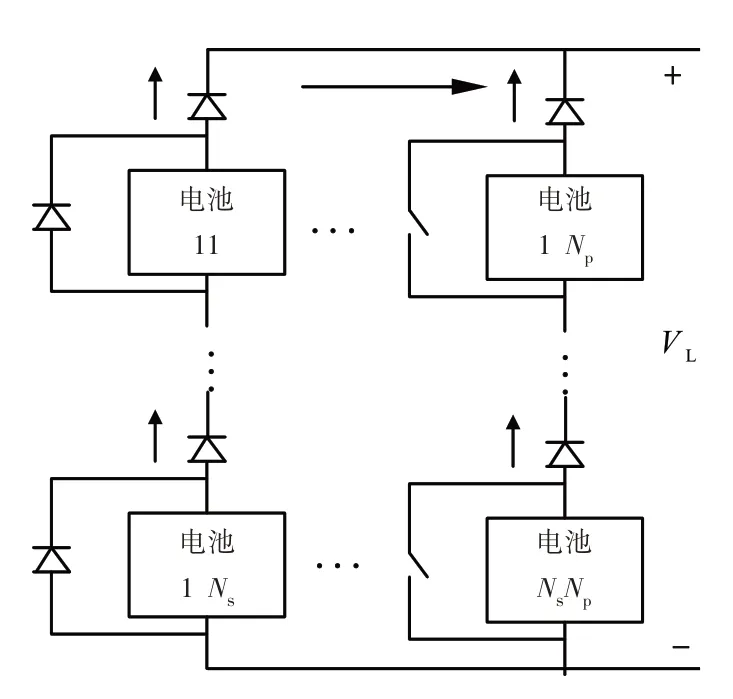
图2 光伏组件模型等效电路
其中Ns是每条支路串联的光伏电池单元数,Np是光伏组件并联支路数.
根据基尔霍夫定律,光伏组件模型中的输出电流和输出电压之间的关系是:
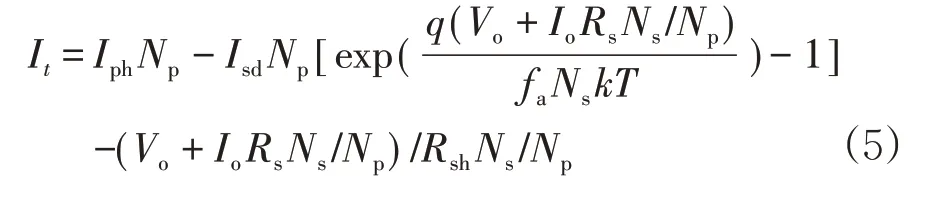
2 精英反向学习粒子群算法
2.1 粒子群优化算法
在PSO 算法中,种群中的每个粒子代表优化问题解空间的一个潜在解,粒子i的速度和位置分别用速度向量Vi={vi1,vi2,...,vid} 和位置向量Xi={xi1,xi2,...,xid}表示,其中d是解空间的维数.每个粒子的速度和位置在一定范围内随机初始化,在进化过程中,粒子i在第d维的速度和位置更新公式为:[12]
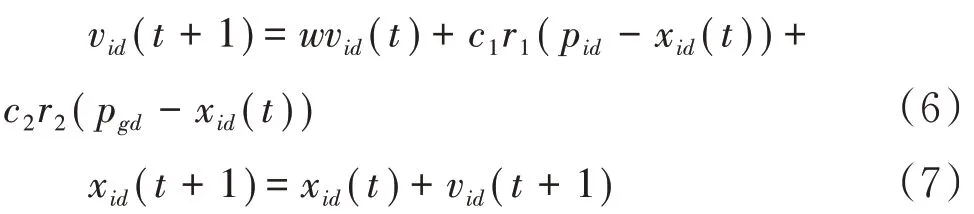
其中ω为惯性权重,c1和c2为加速因子,r1和r2为[0,1]区间内均匀分布的随机数,Pid为种群中第i个粒子找到的最优解,Pgd为种群中所有粒子找到的最优解.
2.2 精英反向学习
作为群体领导者,精英粒子引导着群体中其他粒子飞行,一旦精英粒子陷入局部最优,所有粒子的速度都会减小,甚至停滞,导致整个种群难以跳出局部最优状态.精英学习机制可以给种群中的精英粒子提供一个动量,协助精英粒子跳出局部极值点,从而引导其他粒子向着全局最优解方向飞行.反向学习机制是由Tizhoosh 提出的一种用于提高各种优化算法搜索性能的寻优机理[13].其主要思想是将当前搜索空间的解映射到另一个空间,算法在当前搜索空间和映射空间中并行搜索,这样具有更大的概率搜索到最优解.基于反向学习机理操作可以促使群体进化过程的跃变,从而使算法具有较快的收敛速度,同时又有助于种群在演化过程中能保持较好的多样性,不容易陷入局部最优.反向学习机理如下:
定义1.假设实数x∈[a,b],则定义͂=a+b-x为实数x的反向点.
定义2.假设p=(x1,x2,···,xd)是d维空间中的一个点,其中,xi∈[ai,bi],∀i∈(1,2,···,d),则定义反向点,其中=ai+bi-xi.
定义3.由定义1 与定义2 可知,假定p=(x1,x2,···,xd)是d维空间中一个点,又假设f(⋅)是衡量该点的适应度函数,根据反向点的定义,令为p=(x1,x2,···,xd)的反向点,如果满足f()≥f(p)(计算符号“≥”为优于),则向量代替向量p,否则继续采用向量p,同时评价p点和其反向点的适应度得到相对最优点,从反向学习机理可知,其搜索空间不断地向目标空间靠近,反向学习搜索空间跃变示意(一维空间、二维空间以及多维空间)如图3(a)所示[14].
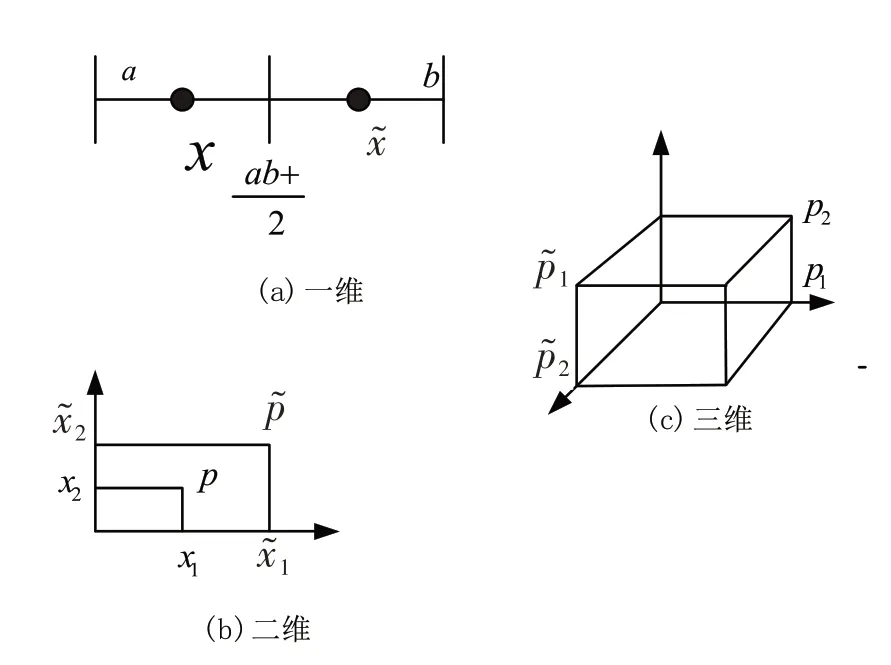
图3 搜索空间反向学习示意图
由于基本粒子群算法在解决复杂工程优化问题时容易出现早熟收敛、陷入局部极值点的缺陷,为了提高基本粒子群算法的性能,将精英反向学习策略融合到PSO 中,在群体的进化过程中,以概率p0执行精英反向学习策略.在执行精英反向学习策略时,先找到当前种群中的若干个精英个体,计算出当前种群中每个个体的精英反向解,从而生成一个精英反向种群,最后将产生的精英反向种群与当前种群一起竞争,选择出优秀个体作为下一代种群.
为减小计算复杂度,本文的反向学习按照一定概率进行,具体实现如下:
设定一个反向学习概率随机p0(p0∈[0,1],且为一个常数),产生一个[0,1]之间的数rand1,如果rand1<p0,则进行反向学习;否则,不进行反向学习.
2.3 柯西变异
为了避免算法出现停滞现象,在算法后期,对种群最优值进行停滞判定,根据群体当前状态,经过有限次的探索,种群最优值连续几代没有变化,便可认为算法已陷入局部极值点,存在停滞的可能.群体进化因子定义为:
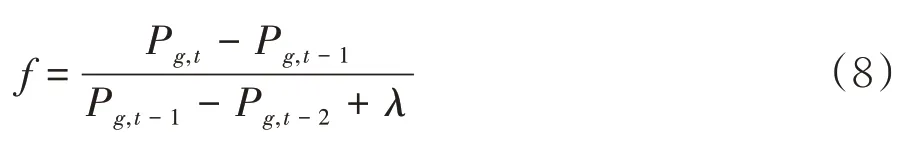
其中,,Pg,t-1,Pg,t-2分别表示第t,t-1,t-2代的最优适应度值,λ为避免分母值为0 而引入的平滑因子.
当最优粒子停滞不前时,对最优粒子进行柯西变异.
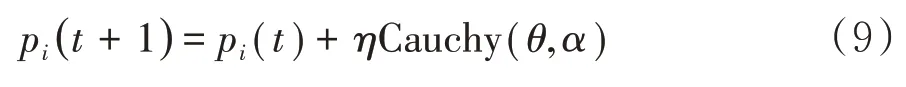
其中Cauchy(θ,α)为标准柯西分布,θ=0,α=1,其密度函数定义为:
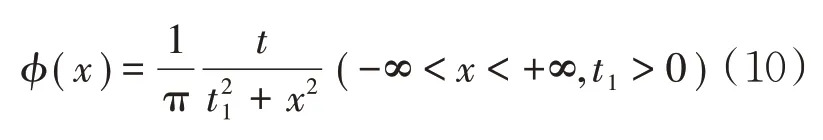
2.4 EOPSO算法执行过程
Step 1:设置种群粒子数Nq、精英学习概率p0,平滑因子λ,最大迭代次数FEs_MAX 等参数值;当前进化代数t=0,当前迭代次数FEs=0;
Step 2:随机产生初始种群,计算每个粒子适应度函数;
Step 3:如果满足终止条件则输出最优值,否则继续执行;
Step 4:产生一个[0,1]内的随机实数rand1;
Step 5:如果rand1 Step 7:根据式(8)判断算法是否停滞,如果停滞,按照式(9)对最优粒子进行柯西变异操作; Step 8: a)计算每个粒子适应度函数; b)根据式(6)和(7)更新每个粒子的速度和位置; c)评价每个个体的新位置,并保存最优解, Step 9:当前迭代次数FEs=FEs+1;,如未到最大迭代次数,转到step 3; Step 10:输出最优解,算法结束. 光伏电池参数估计就是通过实验测量的I-V数据,找到光伏电池参数的最优值,使模型能够准确地描述光伏电池的实际输出特性,使辨识数据与实验数据之间的误差达到最小.因此,误差函数可以定义如下: 式中:e(Vo,Io,θ)为误差函数,表示计算值与实验值之差,θ=[Iph,Isd,fa,Rs,Rsh]为解向量,其元素为待辨识的未知参数. 本文以均方根误差(RMSE)作为目标函数,其定义为: 其中N为实验数据个数. 为了验证EOPSO 算法的性能,将其应用于求解光伏电池参数估计问题.光伏组件由单体太阳能电池(156.5 mm×156.5 mm)串/并联而成.试验温度45 ℃,太阳辐照度1040 W/m2.在标准测试条件下(太阳辐照1000 W/t25 ℃,待辨识参数的取值范围如表1 所示. 表1 单二极管/光伏组件模型待辨识参数范围 表1 (续) 将所提算法与已有的两种算法进行了比较,包括基本粒子群算法,改进综合学习粒子群算法(ICLPSO)[15],所有算法的粒子个数Nq皆设置为50,最大迭代次数为3000,所有算法独立运行30 次.其他参数设置如表2 所示. 表2 算法参数设置 算例中,光伏组件的实验测量数据由26 组电压和电流数据组成.本文在实验I-V 数据建模研究的基础上,采用所提出的EOPSO 算法和其他两种算法对单体二极管电池和光伏组件模型参数辨识.辨识结果如表3 和表4 所示. 由表3 和表4 可以看出,无论是单体电池还是电池组件,EOPSO 算法辨识参数的性能优于其他两种算法. 表3 不同算法RMSE值统计结果(单体电池). 表4 不同算法RMSE值统计结果(电池组件) 将EOPSO 辨识算法得到的参数代入式(4)中,分别以单二极管单体电池和电池组件的电压、电流、功率为坐标轴变量绘制出电池的I-V 及P-V特性曲线如图4 和图5 所示,由EOPSO 算法辨识获得的最优参数重构出单体电池模型和电池组件模型的I-V、P-V 数据与实验测量的I-V、P-V 数据非常接近,这表明本文所提EOPSO 辨识算法获得的电池参数具有较高的准确性,可以精确有效地辨识单体电池和电池组件的模型参数. 图4 单体电池的实验测量数据与算法辨识数据 图5 电池组件的实验测量数据与算法辨识数据对比 为了更直观地比较EOPSO 算法与其他算法的性能,图6 和图7 给出了各种算法的进化曲线.从图6 和图7 可以看出,不管是单体电池还是电池组件,由于初始解是随机选择的,所以每个算法的初始值都较大.随着迭代次数的增加,EOPSO 算法在700代左右迅速收敛到一个相对稳定的目标函数值,其收敛速度较其他两种算法更快,在随后的最优值搜索过程中,可以找到比其他两种算法更小的目标值. 图6 单二极管模型辨识收敛曲线 图7 电池组件模型辨识收敛曲线 快速准确辨识光伏电池模型参数具有重要意义,传统优化算法应用于电池参数辨识时能取得较高的辨识精度,但传统优化算法存在易早熟收敛的缺点.本文提出一种融合柯西变异策略的精英反向粒子群算法(EOPSO).在算法进化过程中,对种群精英个体依照一定概率执行反向学习策略,生成精英反向种群与当前种群进行竞争,精英反向学习策略增加了群体的多样性,提高了算法的收敛速度,当算法陷入停滞时,对最优个体进行柯西变异,避免最优个体陷入局部最优.将改进算法应用于单体电池和电池组件参数辨识,实验结果表明,EOPSO算法能准确辨识光伏电池参数,辨识精度高.3 光伏电池模型参数辨识
3.1 目标函数
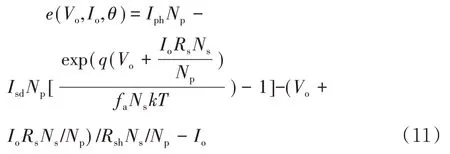
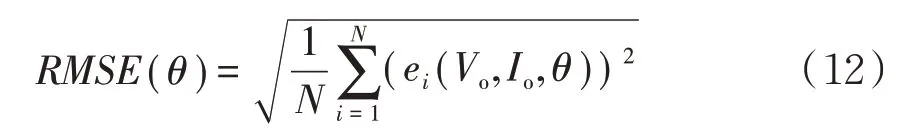
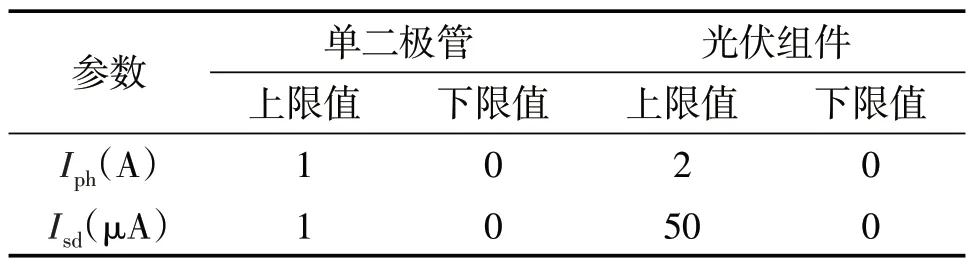
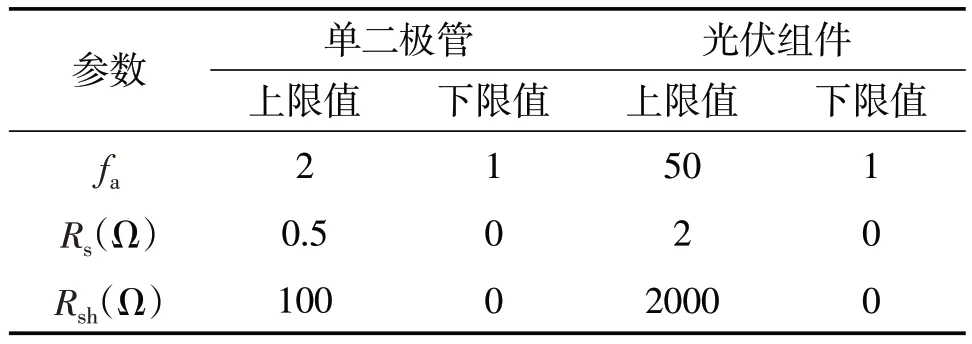
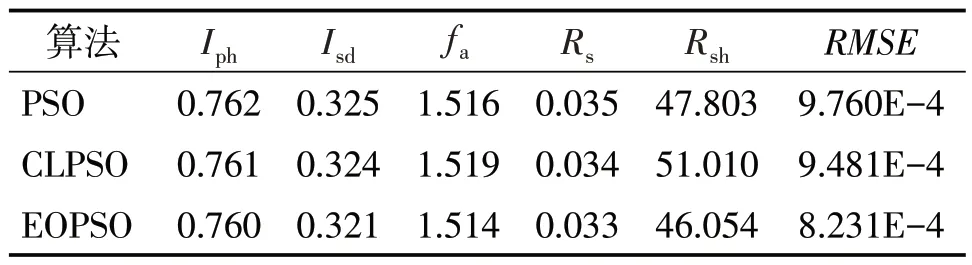
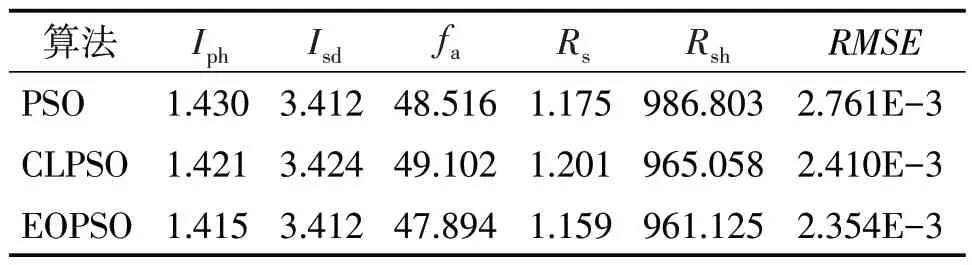
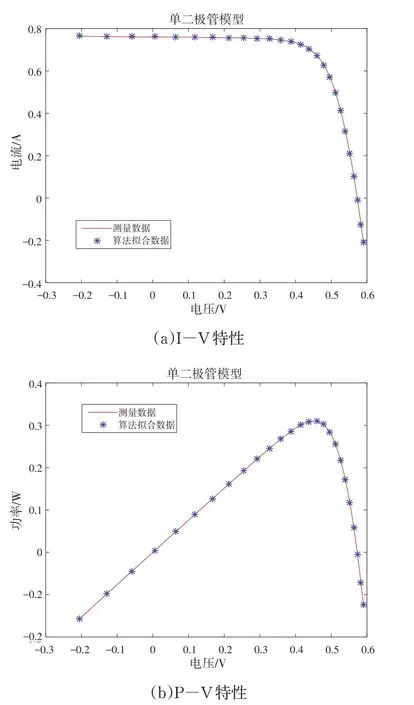
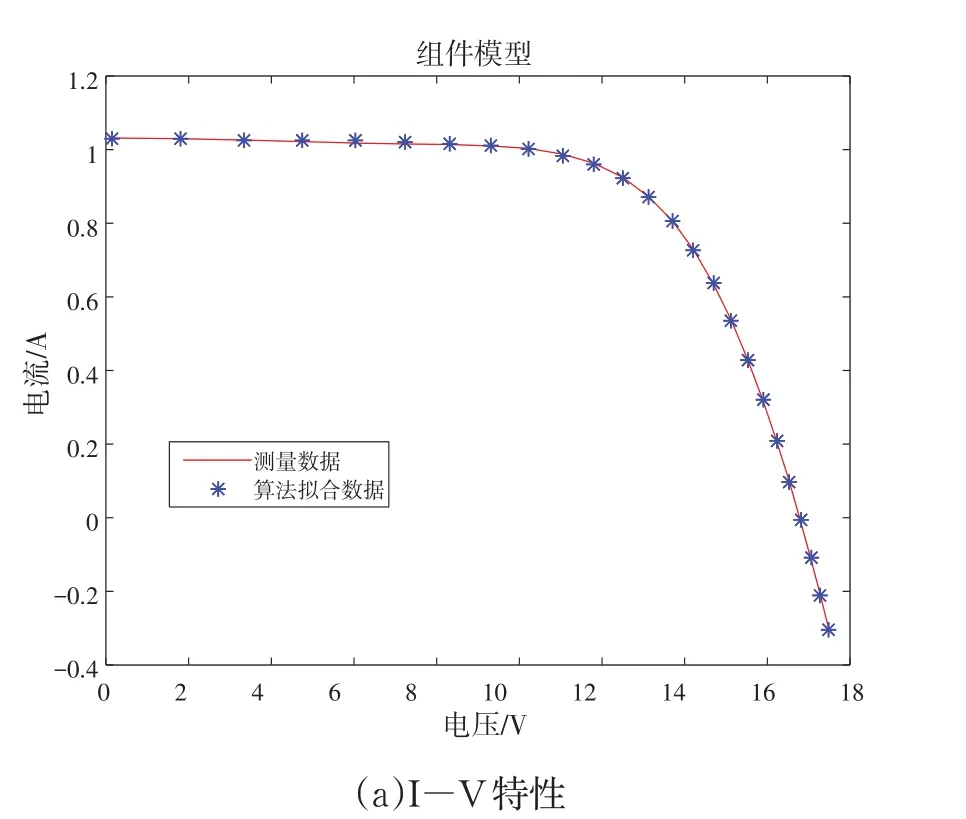
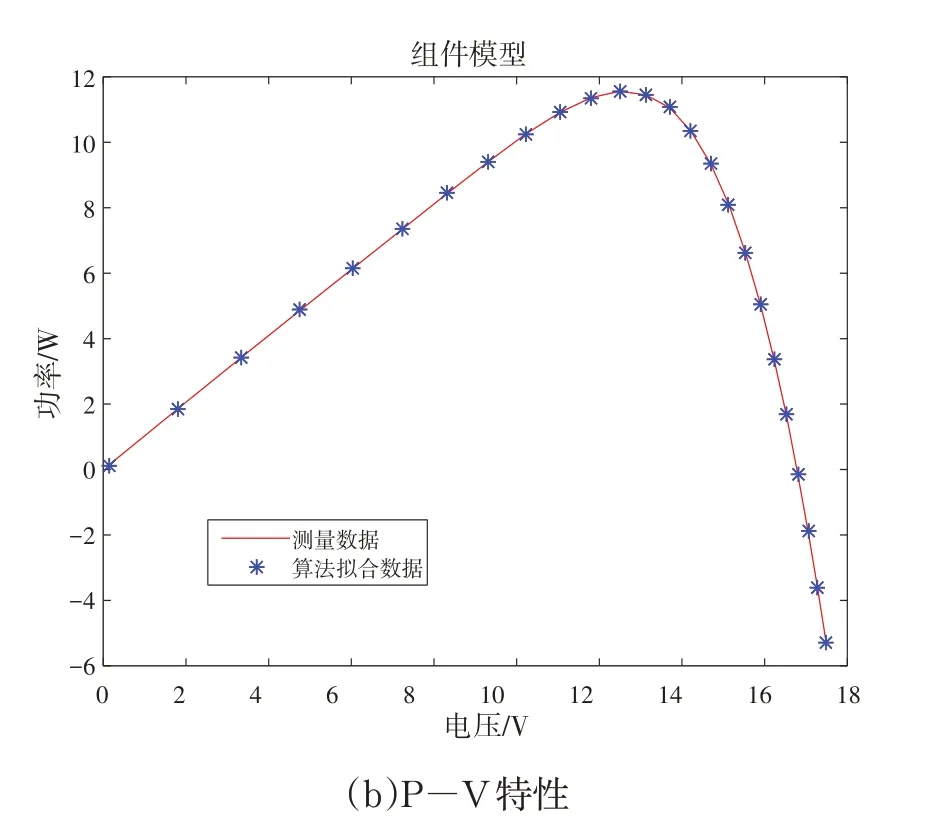
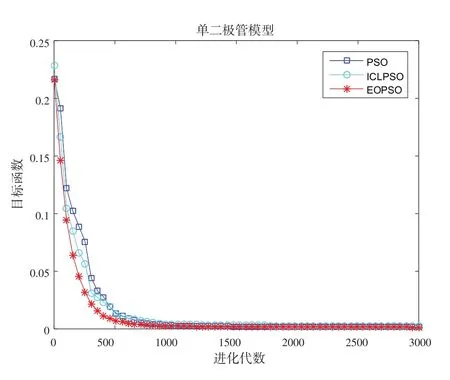
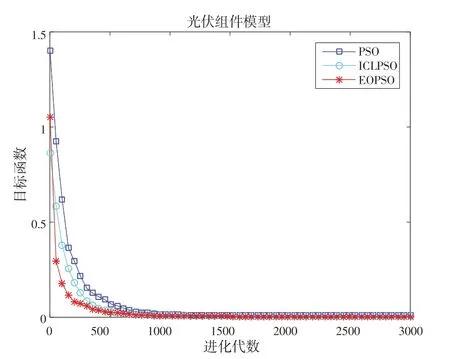
3.2 辨识结果

4 结束语
