高地隙三角履带底盘多体动力学建模与试验

扈 凯 张文毅 李 坤 刘宏俊 祁 兵

(农业农村部南京农业机械化研究所， 南京 210014)

0 引言

履带底盘具有接地比压小、机动性好、转向灵活等特点[1-3]，三角履带底盘在保留了上述优势的基础上，进一步提高了离地间隙，因此在丘陵山地、水田区域被广泛采用[4-5]。三角履带底盘结构较为复杂，加工制造成本高[6-7]，多采用虚拟样机技术进行前期设计和优化。但由于履带底盘拓扑结构复杂，难以准确分析履带与其轮系的受力、运动关系及构建履带路面接触模型，且路谱的不确定性进一步增加了建模难度[8-11],因此履带底盘多体动力学模型的精度一直难以达到要求。

近年来，国内外学者对履带底盘多体动力学的研究主要集中在爬坡越障性能分析、行驶平顺性优化、行驶系统与履带张紧力数学模型构建等方面[12-17]。刘妤等[18]对小型农用履带底盘进行多体动力学建模分析，建立了履带底盘运动学方程，并对模型的驱动力转矩、行驶速度、履带张紧力等参数进行了仿真。潘冠廷等[19]分析了小型山地履带拖拉机爬坡越障性能，求解了最大越障高度的计算公式，并进行了正交试验和单因素变量试验，结果表明，越障速度、坡度角和拖拉机质心位置对履带拖拉机最大越障高度有显著影响。马星国等[20]以高速履带车辆为研究对象，建立了整车动力学模型，获得了履带张紧力、承重轮法向力的仿真结果，仿真数据与理论计算基本吻合。

本文以高地隙三角履带底盘为研究对象，建立履带底盘各组件和车体总成的拓扑结构模型，分析各部分之间的约束和运动关系，推导履带与地面、履带与其轮系的受力关系，采用谐波叠加法构建B级路面(水泥硬质路面)和E级路面(农田软质路面)的路谱，并建立高地隙三角履带底盘的多体动力学模型，对模型进行仿真和履带底盘测试试验。

1 多体动力学模型

1.1 拓扑结构分析

高地隙三角履带底盘由车体和履带行走装置组成，车体包括发动机、座椅总成、车架、油箱等，履带行走装置主要包括驱动轮、承重轮、导向轮、橡胶履带、张紧器等。以某高地隙三角履带底盘为研究对象，底盘主要技术指标如下：整机空载质量1 945 kg；最大爬坡度25°；整机长、宽、高分别为3 400、1 430、1 580 mm；履带总长度为2 350 mm，驱动轮2个，承重轮10个，前后导向轮各2个，其中前侧导向轮受张紧器的作用。在建模过程中，将整个车体简化为一个刚性部件，仅考虑履带、车体和地面之间的相互作用。根据简化后的各部分之间的约束关系建立履带底盘拓扑结构，如图1所示，各部分之间的力和运动副如表1所示。

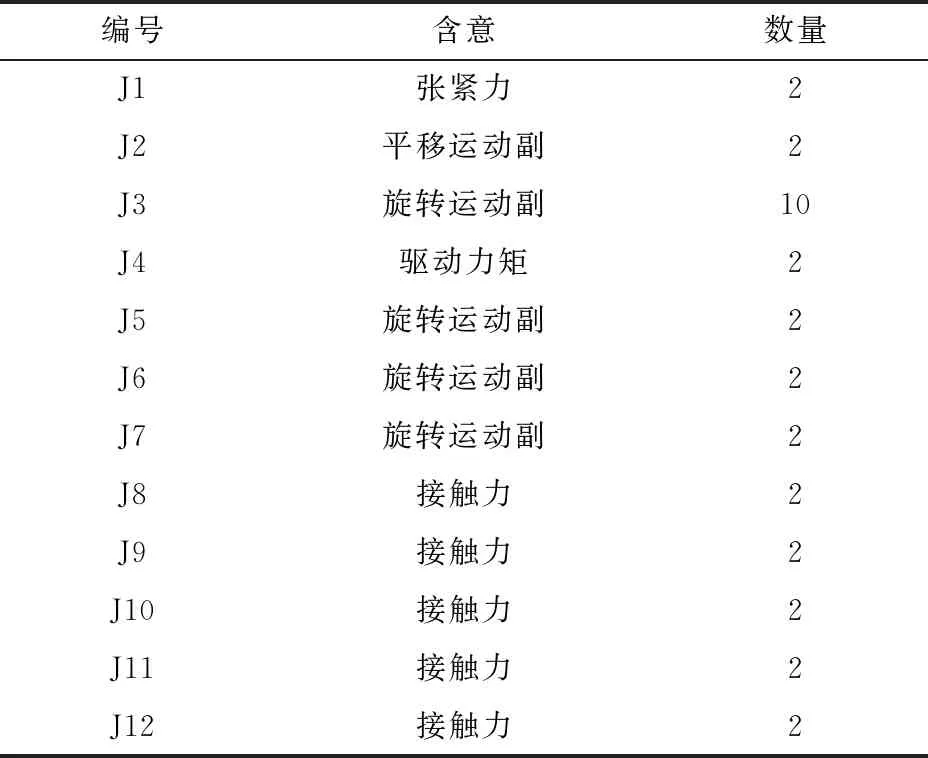
表1 力和运动副

1.2 履带底盘运动学分析

在分析履带底盘运动学时，作如下假设：履带底盘由左侧履带、右侧履带和车体3部分组成；车体与行走部件之间无相对运动；履带长度在行驶过程中不改变；履带与履带轮之间不存在滑移。图2为履带底盘运动示意图。

履带底盘的运动方程为

(1)

(2)

(3)

αk——履带前进方向与运动轨迹的夹角，rad

Δxm——底盘质心x方向的位移，m

Δym——底盘质心y方向的位移，m

同时，定义履带底盘的广义坐标为

Z=(xm,ym,θm)

(4)

对公式(4)求导，同时运用极限理论和瞬态运动分析理论[21]可得

(5)

式中r——履带驱动轮半径，m

dm——左右两侧履带间距，m

d0——履带底盘质心到左右两侧履带驱动轮中心连线的垂直距离，m

qr——右侧履带驱动轮转角，rad

ql——左侧履带驱动轮转角，rad

srx——右侧履带的滑动位移，m

slx——左侧履带的滑动位移，m

履带底盘的运动速度、角速度可通过公式(5)计算求解。

1.3 履带底盘爬坡过程动力学分析

履带车辆在爬坡行进时的受力如图3所示。

在垂直路面方向和平行路面方向的受力平衡方程式分别为

Fz=Gcosα+Fy

(6)

Ft=Gsinα+Ff+Fx

(7)

式中Fz——路面对履带底盘支撑反力的合力，N

G——整机重力，N

Fx——悬挂的工作部件平行于路面方向的作用力，N

Fy——悬挂的工作部件垂直于路面方向的作用力，N

Ff——摩擦阻力，N

Ft——驱动力，N

α——坡度，(°)

根据作用在履带车辆的外力对后导向轮中心(点O2)的力矩方程式，可推导出压力中心横坐标为

(8)

式中xO1——压力中心(点O1)横坐标，m

a——质心沿坡面方向至后导向轮中心的垂直距离，m

w——质心到两导向轮中心连线的垂直距离，m

xc——悬挂的工作部件垂直路面方向的作用力到后导向轮中心的垂直距离，m

yc——悬挂的工作部件平行路面方向的作用力到后导向轮中心的垂直距离，m

h——后导向轮中心至坡面的垂直距离，m

压力中心的位置越靠近后导向轮，履带底盘的俯仰角越大，反之，履带底盘的俯仰角变小。压力中心的位置与履带底盘质心位置、悬挂的工作部件、运动状态、路面对履带支撑力等诸多因素相关。坡度越大，路面对履带底盘支撑反力的合力越大，公式(8)中分母变大，压力中心横坐标后移，履带底盘俯仰角变大；在悬挂工作部件时，重心后移，悬挂的工作部件对底盘的作用力变大，公式(8)中分子变小，压力中心横坐标后移，履带底盘俯仰角变大；当底盘处于加速状态时，驱动力大于摩擦阻力，公式(8)中分子变小，压力中心横坐标后移，履带底盘俯仰角变大。

1.4 承重轮与履带接触模型

在履带底盘行驶的过程中，承重轮承担着车体的重力，还承受地面通过履带传递来的作用力，构建承重轮与履带接触模型具有重要意义。承重轮与履带之间的接触模型可分为3种情况：承重轮悬空；承重轮与履带接触，而对应的履带部分不与地面接触；承重轮与履带接触，对应的履带部分与地面接触。对于第1种情况，承重轮只受重力。对于第2种情况，承重轮所受的力是履带板与承重轮之间作用力矢量的合力。第3种情况最为复杂，其受力分析如图4所示。

地面对履带反作用力可以分解为法向分量和切向分量，法向分量可以表示为沉陷量与沉陷速度的函数，切向分量可以表示为法向分量与履带滑转速度或滑移速度的函数[22]，分别表示为

(9)

T=T(N,vs)

(10)

式中N——地面对履带反作用力的法向分量，N

T——地面对履带反作用力的切向分量，N

z——沉陷量，m

vs——履带滑转速度或滑移速度，m/s

假设地面为硬质地面，则法向力和沉陷量之间的关系可简化为[22]

(11)

同时，假设切向力在相同的滑移速度下与法向力之间呈线性关系，则切向力可简化为

(12)

其中

μ=μ0(1-e-λ|vs|)

(13)

式中μ——摩擦因数

μ0——最大静摩擦因数

λ——系数，一般取0.85

d、j——常数

切向力等于法向力与摩擦因数的乘积，方向与滑移或滑转的速度相反。

1.5 履带张紧力模型

履带底盘在行驶过程中，驱动轮输出驱动转矩，而承重轮、导向轮与履带接触面之间会产生摩擦力以阻碍履带的运动，同时，受张紧器的影响，履带会受到动态张紧力的作用。而履带轮将履带分为多段，某个履带轮前后侧的动态张紧力计算公式为

(14)

(15)

式中Fq——某个履带轮前侧所受的张紧力，N

Fw——某个履带轮后侧所受的张紧力，N

k1——履带拉伸方向的刚度，N/m

bk-1——履带轮前侧拉伸变形后履带长度，m

bk+1——履带轮后侧拉伸变形后履带长度，m

b0——静态时履带长度，m

F0——静态时履带张紧力，N

考虑到履带和地面之间的相互作用，某个履带轮前后侧所受的动态张紧力为

Fw-Fq=Twt

(16)

式中Tw——某个履带轮切向力分量，N

t——单位向量，正负表示切向力方向

由上述分析可知，履带的动态张紧力受到履带的拉伸方向刚度和变形长度的影响，前者由履带的结构和材料决定，而后者较为复杂，受到张紧器作用力、地形、行驶速度等多个因素的影响。

1.6 履带-软地面接触模型

履带与硬地面的接触模型主要受履带对地面的穿透深度、摩擦因数、阻尼系数等因素的影响[22-23]，而履带与软地面的接触模型则更为复杂。履带底盘大多在软地面上行驶作业，建立履带-软地面接触模型尤为必要。

履带和软地面的正压力符合基于贝克的经典压力-沉陷关系模型[22]

(17)

式中p——接地压力，Pa

kc——土壤内聚变形模数，N/mn+1

kφ——土壤内摩擦变形模数，N/mn+2

s——土壤变形指数

b——履带板宽度，m

δ——履带板对地面的穿透深度，m

在软地面行驶过程中，履带对地面的压力使得地面沉降，继而产生了运动阻力，同时，履带会剪切地面，产生的剪切应力所引起的反力即为地面对履带的推力，纵向剪切应力和横向剪切应力表述式为(纵向为履带底盘前进方向，横向为履带底盘左右方向)

(18)

(19)

式中τz——纵向剪切应力，Pa

τh——横向剪切应力，Pa

c——内聚力，Pa

σ——法向应力，Pa

θ——内聚角，rad

R——承重轮半径，m

Cz——纵向阻尼系数

Ch——横向阻尼系数

K——土壤水平剪切变形模数

履带板受到来自软地面的纵向推力和横向推力为

(20)

(21)

式中Fr——纵向推力，N

FH——横向推力，N

L——履带板接地长度，m

Q——履带接地段法向负荷，N

2 仿真模型建立

2.1 底盘三维模型

构建某高地隙三角履带底盘的三维模型，综合考虑各部分质量、连接装配关系、运动关系等因素，所建立的模型如图5所示。由于底盘各部分的质量分布会影响仿真结果的精度，所以对各部分的质量进行对比以消除误差，实际底盘与底盘模型中各部分的质量如表2所示。

由表2可知，所构建的模型中各部件的质量与实际底盘的误差较小，总质量误差为45 kg，误差率为2.37%，说明三维模型具有较好的精度。

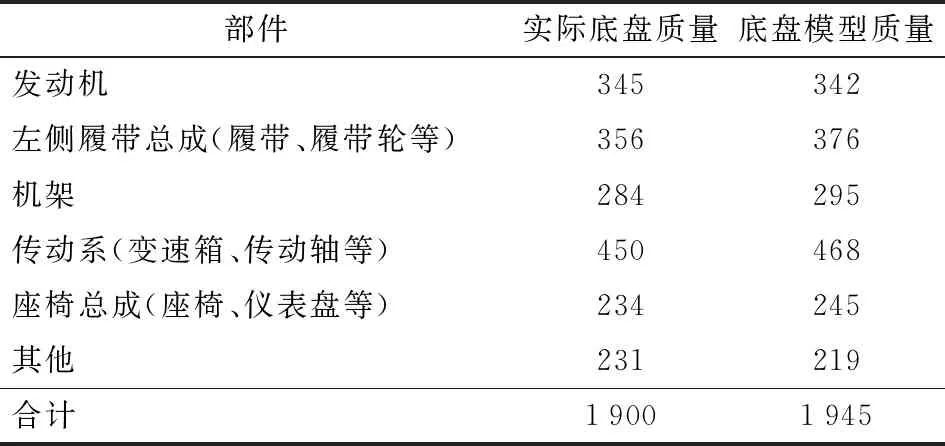
表2 实际底盘与所建的底盘模型中各部分质量

2.2 路面谱模型

路面不平度具有随机、平稳和各态历经的特征，可以用平稳随机过程理论来构建路面谱，通常把与道路垂直纵断面和道路表面的交线作为路面不平度的样本，并通过样本的功率谱密度函数来描述。谐波叠加法是目前最常用的路谱生成方法，其原理是假设路面高程为平稳、各态历经的高斯过程，可以采用不同形式的三角级数来进行模拟，本文采用谐波叠加法来生成路谱模型。

路面位移功率谱密度可表示为

(22)

式中Gd(n)——路面位移功率谱密度

Gd(n0)——参考空间频率n0下路面不平度系数

n——空间频率，m-1

利用平稳随机过程的特性，在空间频率n1和n2之间的路面不平度方差γ为

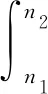
(23)

进一步将n1和n2之间的频率空间划分为k个小区间，每个小区间的中心频率为nmid-k(k=1,2,…,n)，第k个小区间对应的路谱不平度表示为

(24)

式中Gd(nmid-k)——第k个小区间对应的路面不平度系数

Δnk——第k个小区间的长度

θk——相位角

将所有小区间的正弦波函数叠加起来，即可获得随机位移输入。按照国标GB 7031—2005《机械振动 道路路面谱测量数据报告》，水泥路面属于B级路面，软质路面属于E级路面，采用数学软件编制出随机路面程序，每间隔0.25 m生成一个数据点，获取的B级路面和E级路面模型如图6所示。

2.3 路面参数设置

根据底盘试验的实际环境，利用动力学软件构建水泥硬质路面和农田软质路面的模型，两种路面的特征参数如表3所示。在软件中，假设硬质路面不会因履带的碾压产生变形，采用刚体接触摩擦模型来模拟履带和地面之间的相互作用关系，在农田软质路面中，采用1.6节中分析的贝克经典压力-沉陷关系模型来模拟履带和地面之间的相互作用关系。

表3 两种路面的特征参数

3 仿真分析与试验验证

将三维模型导入动力学软件进行仿真，在软地面行驶仿真模型中建立1.6节中分析的贝克经典压力-沉陷关系模型，在硬地面行驶仿真模型中采用软件自带的刚体接触摩擦模型。将2.2节中构建的路面谱以mat文件格式导入形成多个坐标点，连接各个坐标点以形成路面模型，设置各部件之间的旋转副、固定副等运动关系和力学参数。仿真模型如图7所示。对高地隙三角履带底盘样机进行试验测试，在驱动轮处安装旋转编码器以获取实时转速，继而可获取整机实际行驶速度，编码器每转产生600个脉冲，同时，在拖拉机座椅下方安装有水平倾角传感器以获取底盘的俯仰姿态，由高精度数据采集卡采集水平倾角传感器输出的0～5 V电压。试验现场如图8所示。

3.1 直线行驶速度

对高地隙三角履带底盘分别在硬质路面和软质路面的直线行驶速度进行仿真和试验测试，发动机油门固定在理论行驶速度1.50 m/s的位置，通过编码器的脉冲数计算出实际行驶速度。相较于轮式机械，履带对地面具有较好的附着能力，其在硬质路面的滑转率低于1%，在软质路面滑转率低于2.5%[24-25]，故试验测试不考虑履带打滑的影响。每间隔0.20 s采集一次数据，仿真步长设置为0.20 s。仿真获取的行驶速度变化曲线如图9所示，测试获取的行驶速度变化曲线如图10所示。

由图9可知，在硬质路面上，仿真获取的平均速度为1.486 m/s，最大速度为1.511 m/s，最小速度为1.462 m/s，标准差为0.014 13 m/s。在软质路面上，仿真获取的平均速度为1.492 m/s，最大速度为1.540 m/s，最小速度为1.432 m/s，标准差为0.030 7 m/s。由图10可知，在硬质路面上，试验获取的平均速度为1.477 m/s，最大速度为1.530 m/s，最小速度为1.430 m/s，标准差为0.031 63 m/s。在软质路面上，试验获取的平均速度为1.472 m/s，最大速度为1.549 m/s，最小速度为1.391 m/s，标准差为0.043 98 m/s。实测的行驶平均速度略低于仿真的行驶平均速度，在硬质路面和软质路面的平均速度误差率均小于1.50%。当履带底盘在软质路面行驶时，速度的标准差较大，这意味着速度在一定范围内存在较大的波动。

3.2 直线行驶偏移量

对履带底盘分别在硬质路面和软质路面的直线行驶偏移量进行仿真和试验测试。试验设置如下：使用标记线以履带右前方地点为起点，沿着履带方向向前标定30 m作为终点；履带底盘以1.5 m/s速度前进；每种路面测试3次；驾驶员在初始时刻将方向调正，在行驶过程中不再对方向盘进行操作。仿真和试验测试数据如表4所示。

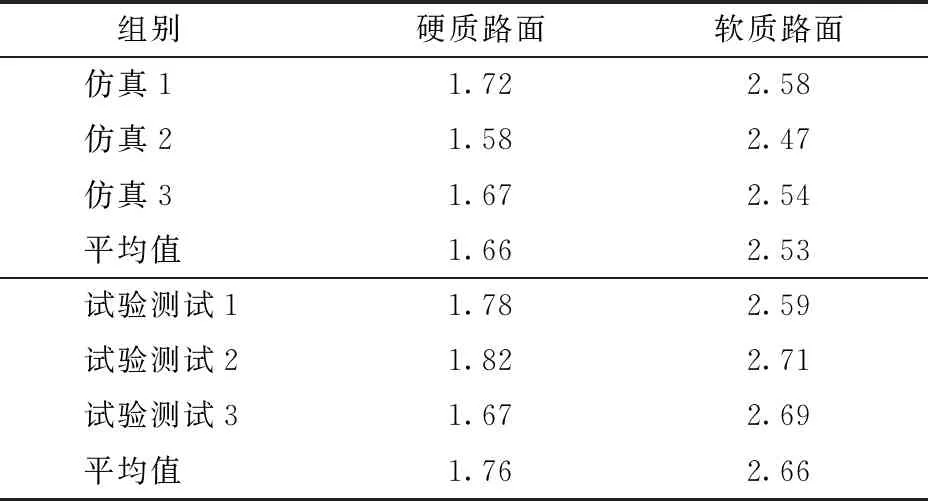
表4 行驶偏移量仿真和试验测试结果

由表4可知，在硬质路面上，仿真和实测的行驶偏移量为1.66 m和1.76 m，误差率为5.68%，在软质路面上，仿真和实测的行驶偏移量为2.53 m和2.66 m，误差率为4.89%。

GB/T 15370.4《农业拖拉机通用技术条件 第4部分：履带拖拉机》中规定，履带拖拉机在干硬平整、纵横坡度不大于1%路面上的跑偏量应不大于6%，本文仿真和测试的硬地面行驶的最大跑偏量分别为5.73%和5.86%，满足国标规定的要求。

3.3 爬坡过程俯仰角

对履带底盘行驶速度分别在1.0 m/s和1.5 m/s下在硬质路7.5°坡面爬坡过程中的俯仰角进行仿真和试验测试。在0～2 s的过程中，履带底盘速度由0均匀加速至1.0 m/s或1.5 m/s，在2～5 s的过程中，履带底盘速度稳定不变，采样和仿真计算步长均为0.1 s。俯仰角变化曲线如图11所示。

由图11可知，在速度1.0 m/s时，对于0～2 s的加速工况，俯仰角仿真平均值为7.936°，俯仰角实测平均值为8.173°，误差率为2.90%，对于2～5 s的匀速工况，俯仰角仿真平均值为7.672°，俯仰角实测平均值为7.823°，误差率为1.93%，仿真和实测的俯仰角最大值分别为8.246°和8.443°。在速度为1.5 m/s时，对于0～2 s的加速工况，俯仰角仿真平均值为8.155°，俯仰角实测平均值为8.400°，误差率为2.92%，对于2～5 s的匀速工况，俯仰角仿真平均值为7.805°，俯仰角实测平均值为8.044°，误差率为2.97%，仿真和实测的俯仰角最大值分别为8.497°和8.785°。综上所述，当加速工况时，平均俯仰角的误差率相对较大，但不超过3.0%，当速度为1.0 m/s匀速工况时，平均俯仰角的误差率不大于2.0%，当速度为1.5 m/s的匀速工况时，平均俯仰角的误差率不大于3.0%。故仿真与实测的俯仰角吻合度较好，所建立的多体动力学模型具有较高的精度。

4 结束语

以高地隙三角履带底盘为研究对象，分析了各部件之间的受力和运动关系，以理论分析、建模仿真和试验验证相结合的方法对履带底盘的动力学特性进行研究，采用谐波叠加法构建了B级路面(水泥硬质路面)和E级路面(农田软质路面)的路谱，并进行模型仿真与测试验证。结果表明：在硬质路面和软质路面上，平均速度误差率均小于1.50%，行驶偏移量误差分别为5.68%、4.89%，平均俯仰角误差不大于3%。试验表明，所构建的高地隙三角履带底盘多体动力学模型具有较高的精度，可用于理论仿真分析，为履带底盘动力学分析与优化提供支撑。