基于三维激光扫描技术的盾构隧道变形分析

王 鑫 景 冬 徐 飞 刘洪涛

(1. 山东科技大学 测绘与空间信息学院, 山东 青岛 266590; 2. 济南市勘察测绘研究院, 山东 济南 250000)

0 引言

近年来,随着城市的不断发展,地铁建设的高速推进。在隧道建设过程中,地面设施的建设、不同区段地理环境的差异等因素,都会使地铁隧道发生一定程度上的变形,当变形程度超过限定要求时会严重影响隧道的结构安全[1-2]。地铁隧道竣工后需要检测其超欠挖是否合理、横断面与设计值的误差量。地铁隧道距离长、分布区域广,需要在天窗时间测量,因此对测量手段要求较为苛刻[3]。传统方法通常采用全站仪、断面仪等设备进行特征点位测量。全站仪采用单点测量,具有较高的精度,但存在测量速度慢、采集的数据量有限等缺点[4-5];另外断面仪测量时只能获取一个断面信息,在长距离隧道检测中,作业效率低[6-7]。综上所述,传统方法的数据采集量少,工作量较大,工作效率较低,短时间内无法全面反映隧道的变形状况。

三维激光扫描技术近年来发展迅速,受到人们的广泛关注,相比于传统测量方法具有高速度、高效率等特点,在地铁隧道监测领域的应用具有广阔的应用前景[8]。李珵等[9]将三维激光扫描技术用于地铁隧道检测,其精度可以满足施工要求。曹先革等[10]通过对三维激光点云数据进行处理,测得隧道断面误差精度在10 mm左右。三维点云数据能够更加详细地反映隧道整体的轮廓趋势,通过对三维点云数据进行处理并提取相关参数,可以对隧道整体进行变形分析。本文基于三维激光点云对盾构隧道进行监测,在测量过程与数据处理上做了说明,并与全站仪测量数据进行联合分析。通过对两种仪器数据的对比来显示三维激光扫描技术中隧道监测的形变特点和技术优势,从而更好地指导隧道验收。

1 基本原理

地面式三维激光扫描系统以自身为原点建立坐标系,通过计算距离及角度信息来确定目标的坐标。通过激光测距的原理获取被测目标到仪器中心的距离R,再获取在水平方向及竖直方向上对被测目标的扫描角度,即可求得任意点在坐标系内的坐标值。可表示为:

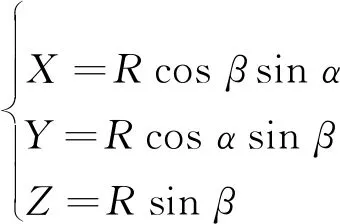
(1)

式中,X、Y、Z表示点云的坐标值;R表示被测距离;α、β表示扫描仪在水平方向及竖直方向上扫描的角度。

2 外业数据采集

在开始采集数据之前,首先要根据隧道的具体情况布设测站,在保证点云扫描质量的情况下,尽量减少测站数,减少点云拼接误差[11];根据实际情况,设置符合工程需求的最佳扫描分辨率;由于三维激光扫描仪测距精度上的限制,每扫描完一段区域后需要转移测站使得各测站间数据相互独立,因此需要在两测站之间布设不少于3个标靶球作为公共点,方便后期数据拼接;在准备工作完成之后,即可开始对隧道进行扫描。

3 数据处理

由于原始数据未对测站数据进行拼接,同时含有大量的噪声点,并不能直接进行使用。因此,需要对数据进行拼接、去噪、轴线及轮廓线提取等操作,才能对隧道的变形状况进行分析,具体内容如下文所示。

3.1 点云拼接

上文提到,由于三维激光扫描仪各测站间的数据相互独立,因此,采用布尔莎模型将各测站的点云数据转化到同一坐标系下。在扫描仪参数不变的情况下,可认为各测站的尺度因子k不变,在拼接时只需计算旋转参数εx、εy、εz和平移参数ΔX、ΔY、ΔZ即可。通常情况下至少需要3个标靶点才可进行求解,假设某一标靶在第一测站中的坐标为(Xt,Yt,Zt),在第二测站中的坐标为(xt,yt,zt),则二者关系为:

(2)

式中,εx、εy、εz为旋转参数;ΔX、ΔY、ΔZ为平移参数。利用最小二乘法求解出转换参数后,即可进行点云拼接。

3.2 中轴线拟合

在监测中,隧道中轴线常用于表示隧道的整体姿态和走向[12-13]。将拼接好并去噪后的点云数据投影到水平面XOY上,利用角准则提取边界点。如图1所示,从x轴正方向起分别测量点P附近点Pi之间连续夹角的差值Δαi,若存在Δαi大于设定阈值Tα,则点P为边界点。其中,图1(a)为内部点与i个邻近点形成的夹角,图1(b)为边界点与i个邻近点形成的夹角。将提取出的边界点进行曲线拟合,取其均值作为初始中线。

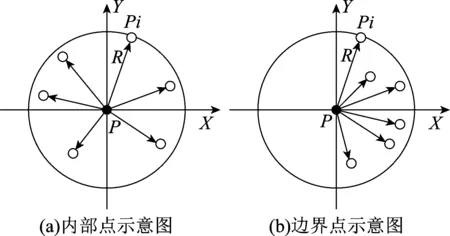
图1 边界点提取原理

为提升中线的精度,在初始中线的基础上使用最小二乘法再次拟合,设拟合函数为

S(x)=α0φ0+α1φ1+…+αnφn

(3)

对于初始中线坐标(xi,yi),存在函数y=S*(x)得到

(4)

式中，ωi表示在点(xi,yi)重复观测的次数。将公式(4)转化为求方程

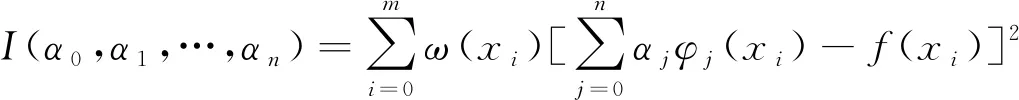
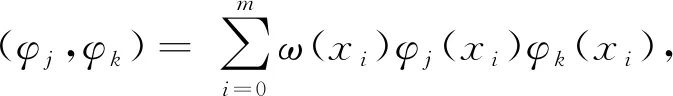
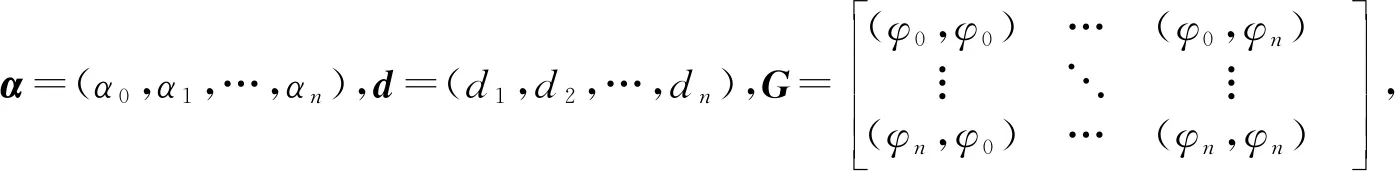
(5)

3.3 断面提取及分析

在拟合出的中线上任取一点Pi(Xi,Yi,Zi),计算过点Pi的切向量ni(l,m,n),则过该点的法平面方程为

l(x-Xi)+m(y-Yi)+n(z-Zi)=0

(6)

(7)

将符合要求的点云数据绕Y轴和Z轴旋转进行坐标转换,令切向量ni平行于z轴,其目的是为了让断面内的点在旋转后z方向上坐标等于0,将其投影到XOY面上;将三维点云数据转化为二维平面数据进行变形分析,简化数据分析难度,故只需要在XOY面内分析断面的变形情况即可。

地铁隧道在设计之初为圆形结构,但由于周围岩层压力分布上的不均匀会导致隧道发生收敛变形,隧道管片逐渐失圆呈椭圆形。为了能够直观地了解隧道的变形状况,需要对提取出隧道断面进行椭圆拟合。将拟合出椭圆的长半轴及短半轴与设计参数进行对比,分析形变量的大小并采取相应措施避免相应问题的发生。为此,本文采用最小二乘法进行椭圆拟合,其步骤如下所示。

设平面内任意位置椭圆方程为

x2+Axy+By2+Cx+Dy+E=0

(8)

设点Pi(xi,yi)(i=1,2,...,n)为断面轮廓上的n个测点。根据最小二乘法原理,目标函数为

(9)

为求函数中A、B、C、D、E的值,至少需要5组测点。所以对A、B、C、D、E求偏导,使

(10)

(11)

通过对方程的求解即可得到A、B、C、D、E的值。得到椭圆方程后,根据椭圆的几何性质得到椭圆圆心位置(x0,y0)及长短半轴a、b的值。

(12)

将椭圆拟合得到的横断面与设计横断面进行比较,求取隧道变形量。以拟合椭圆的中心O为圆心,断面设计半径R做圆。如图2所示,计算实测断面轮廓点到设计断面上的距离AB,即可求得其形变量Δ。

图2 形变量分析

Δ(AB)=OA-OB

(13)

4 实验分析

本实验选择济南某条建设中的地铁隧道,测试区域长度约180 m。实验设备使用Trimble TX8地面式三维激光扫描仪及Leica TS09全站仪进行测量。本实验在VC++环境下编写相关算法对点云数据进行处理,后期利用CloudCompare软件处理并实现数据的可视化。本次实验共扫描点位10 540 762个,对点云原始数据进行拼接、去噪、简化后剩余点数为10 518 516个。

将处理过后的点云数据投影到XOY平面上,利用角准则法则提取出隧道的边界点,对边界点进行曲线拟合,取两条拟合曲线的均值作为初始中线。在初始中线的基础上利用最小二乘法精确拟合,如图3所示。

图3 边界点及中轴线

选取其中10个断面进行分析,全站仪实测的断面中心与扫描仪实测的断面中心进行对比,结果如表1所示。

(14)

从表1可以看出,两种仪器测量得到的断面中心在X轴方向上的偏差最小为1.1 mm,最大为2.6 mm;在Y轴方向上的偏差最小为1.3 mm,最大为3.6 mm。根据中误差公式(14)计算得到X方向上的中误差σx=2.04 mm;Y方向上的中误差σy=2.75 mm;点位中误差σp=3.42 mm。证明了三维激光扫描技术的可以达到毫米级的测量精度。将这10个拟合后的横断面的长半轴a和短半轴b与隧道设计半径R=2.9 m进行对比,如表2所示。

表1 断面中心数据对比表

从表2可以观察得出,三维激光扫描系统测量得到的横断面长半轴(a)最大形变量为1.04 cm,短半轴(b)最大形变量为-1.09 cm。全站仪系统测量得到的横断面长半轴最大形变量为1.05 cm,短半轴最大形变量为-1.06 cm。如图4所示,两种仪器测得的长半轴之差最大为3.3 mm,最短为0.1 mm,中误差为1.92 mm;短半轴之差最大为2.9 mm,最小为0.3 mm,中误差为1.64 mm,总体中误差为2.53 mm。证明了三维激光扫描仪在精度上的可靠性。

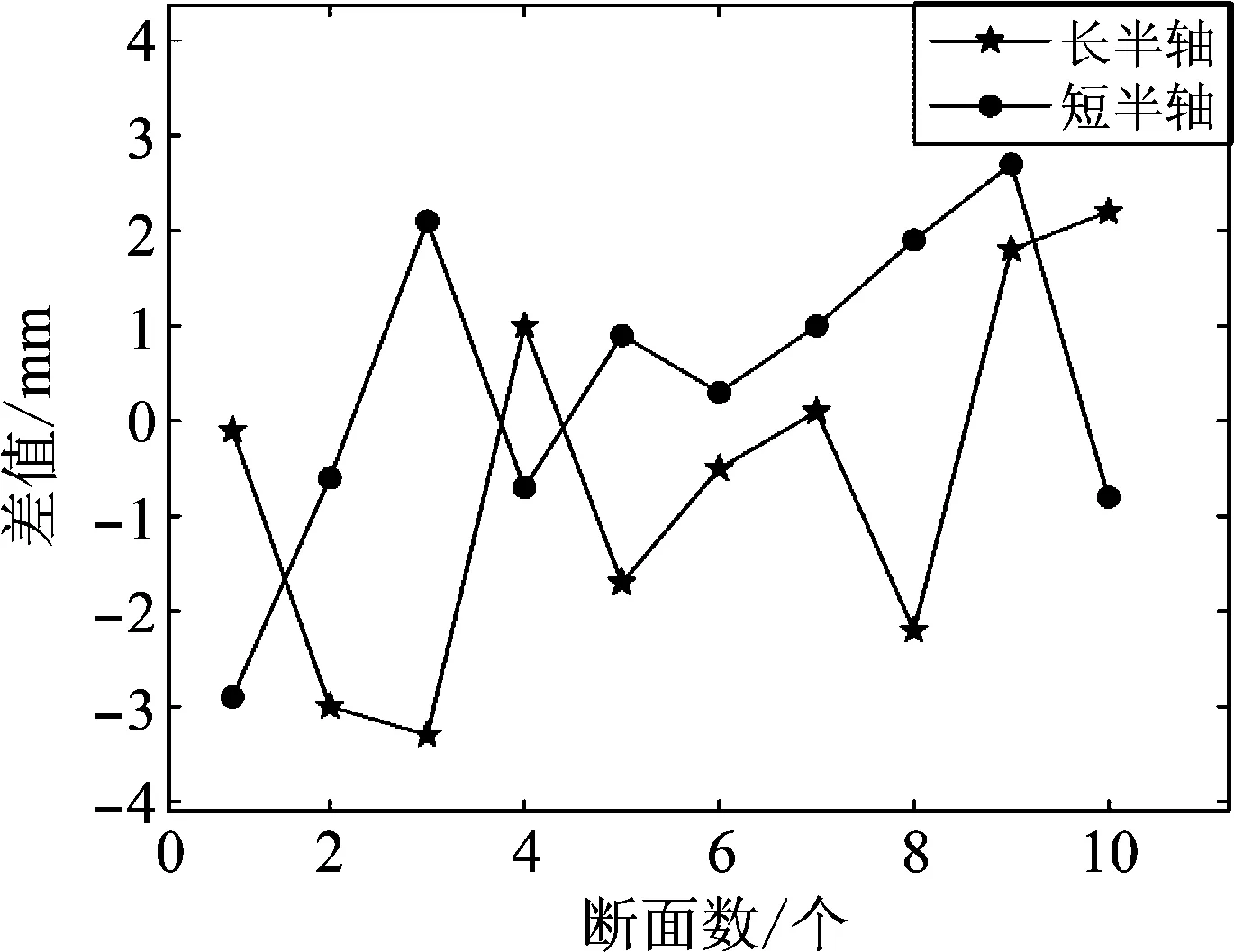
图4 扫描仪全站仪测量结果差值

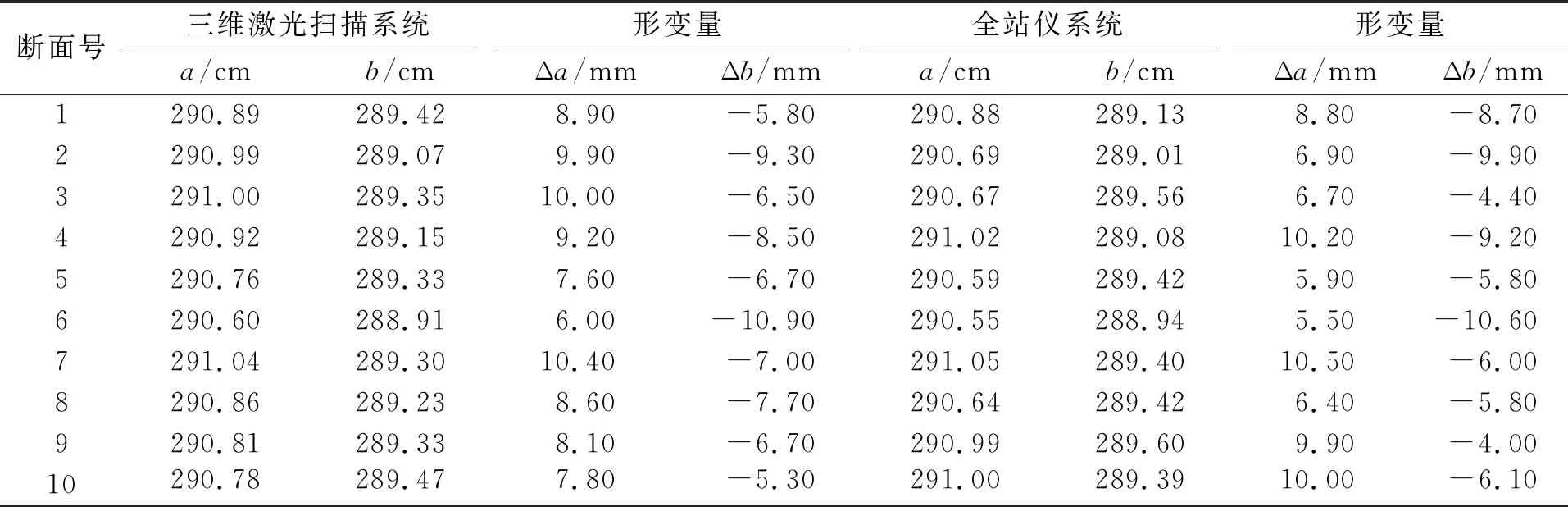
表2 横断面半轴长度对比表

对三维点云中提取出的剩余横断面的长短半轴形变量进行分析,如图5所示。长半轴最大形变量为3.32 cm,平均形变量1.19 cm;短半轴最大形变量为-2.08 cm,平均形变量-0.74 cm。可以看出,水平方向的形变量多为正值,竖直方向上的形变量多为负值,说明隧道整体在竖直方向上的受力大于水平方向上的受力,使得隧道整体表现为水平方向外凸,竖直方向下沉的状态。断面77长半轴的形变量大于3 cm,短半轴形变量大于2 cm,其周围断面的长短半轴形变量也接近2 cm,说明该区域受到的应力较大,应加强此区域监测。

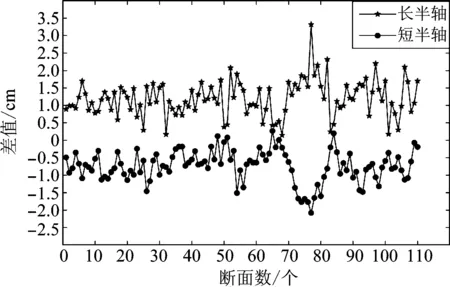
图5 整体形变量

5 结束语

本文介绍了三维激光扫描系统在隧道检测中数据采集的原理及数据处理流程。采用最小二乘思想对隧道中线及横断面进行拟合;经计算,两种仪器测得断面中心坐标在X方向上的中误差为2.2 mm,Y方向上的中误差为2.61 mm,点位中误差为3.41 mm;测得的长短半轴之差均小于4 mm;说明三维激光扫描系统在测量精度上可达到毫米级。通过分析得到隧道整体表现为水平方向外凸,竖直方向下沉的状态,其中水平方向及竖直方向变形量集中在-0.02～0.02 m。证明了三维激光扫描系统在测量精度上的可靠性,相比于传统测量系统可以做到对检测目标变形情况进行整体分析,在地铁隧道施工建设中有着广阔的发展前景。本文方法在中轴线及横断面提取上达到了较高精度,但在点云缺失程度较大时横断面的提取鲁棒性不足,今后应在相关算法上做进一步研究。