基于Adams仿真分析多边形效应和磨损链轮对链系统运行的影响

2021-07-27刘振振付振明

现代制造技术与装备 2021年6期

刘毅刘振振付振明

（青岛征和工业股份有限公司，青岛 266700）

链传动相对带传动有着平均传动比准确、无滑动、结构紧凑及传动效率高的特点，在温度较高、恶劣环境下也可以正常作业，所以在汽车、摩托车、农业、石油器械等领域有着广泛应用[1]。但是，链传动由于结构特点瞬时传动比不稳定，传动时存在噪声、冲击等问题[2]。链系统多在高速、多冲以及交变的工况下运行，因此在日常生产应用中链传动的失效形式主要有链板疲劳断裂、链条磨损伸长、链轮齿部磨损及断裂等[3]。所以，分析链传动系统的失效模式具有重要意义，可为以后链传动系统的优化设计提供一定的数据支持。本文利用Adams对链传动系统进行虚拟仿真，重点分析链条多边形效应对链系统的影响和链轮齿部不同磨损状态下的链系统运动和受力情况。

1 链传动特性分析

如图1所示，链传动与围绕多边形运动的带传动类似。当链条绕在链轮上时呈多边形，多边形的边长等于链条的节距P，而链轮的齿数相当于多边形的边数。

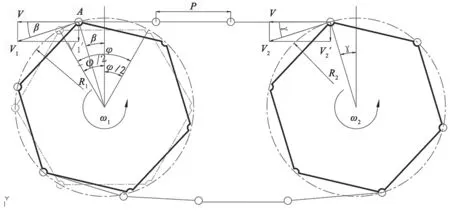
图1 链传动运动示意图

如果两个链轮的齿数分别为Z1、Z2，那么当链轮转速分别为n1、n2时[4]，有：

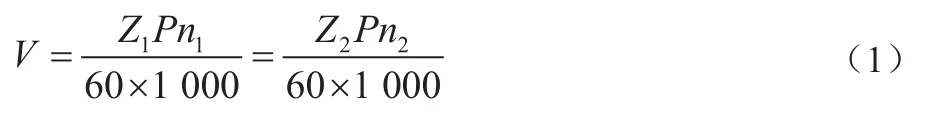
传动比i为：

为了便于分析，假设主动链轮角速度为ω1，从动链轮角速度为ω2，将链条运动速度V1分解成垂直方向的分运动V1´和水平方向的分运动V，那么有：

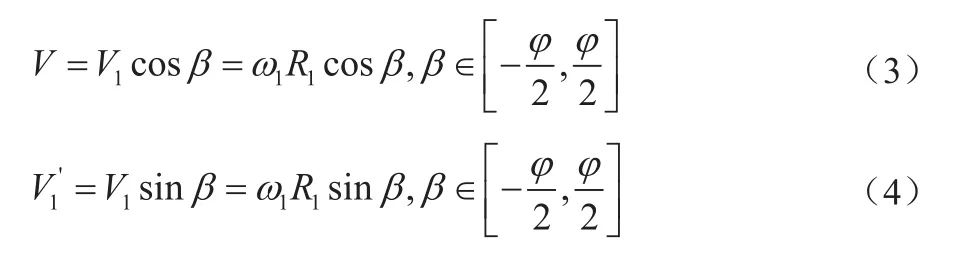
（1）当β=0°时，有：

在链系统运动过程中，β在之间变化时，水平速度V将经过最小到最大再到最小的变化，而垂直速度V1´将经过最大到最小再到最大的变化，呈周期波动。

链条在主动链轮与从动链轮上运动的水平分速度是相等的，所以从动链轮角速度可以表示为：

如果主动链轮的角速度在不断变化，那么从动链轮的角速度也在相应不断变化；如果主动链轮角速度恒定，那么从动链轮的运动将周期变化。

从以上分析可以看出，β和γ的大小决定了速度的变化范围，所以可以通过减小β和γ角度变化范围的方式使多边形效应对链系统的影响降到最低。

2 链传动系统建模及仿真分析

2.1 建立链传动模型

在Adams中可以利用自带的链系统模块快速建立链传动系统。

系统建立过程主要包括以下几个步骤：

（1）建立主动链轮和从动链轮，如果有张紧轮或张紧导轨，可同步建立；

（2）建立链条；

（3）对链轮和链条进行组装，在链条和链轮自动装配过程中，链轮和链节、链节和链节之间的约束自动生成；

（4）施加激励和约束。

本文分析所用链传动参数如表1所示。

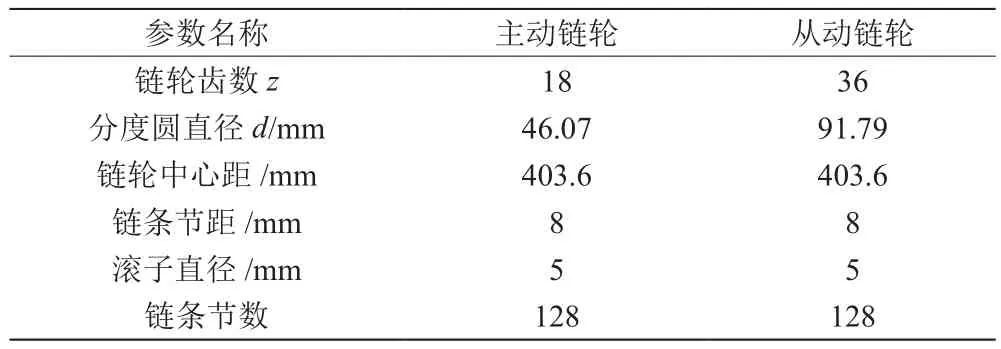
表1 链传动系统主要参数

根据以上步骤和参数建立的仿真模型，如图2所示。

图2 链传动仿真模型

2.2 链传动模型仿真及分析

令模型在空载下运行，为了减小冲击，提高仿真结果的准确性，采用step函数，使链轮在0.2 s内由0 r·min-1加速到600 r·min-1，然后保持该速度运行。仿真步长设置为100，仿真时间设置为0.4 s。链系统运动特性仿真结果，如图3所示。

图3是主动链轮与从动链轮的角速度变化曲线，其中实线代表主动链轮，虚线代表从动链轮。从动链轮角速度为主动链轮的1/2，验证了模型的准确性。从图3可以看出，主动链轮角速度曲线较为平稳，而从动链轮角速度曲线呈上下波动，说明由于链传动的多边形效应引起的角速度周期性波动。

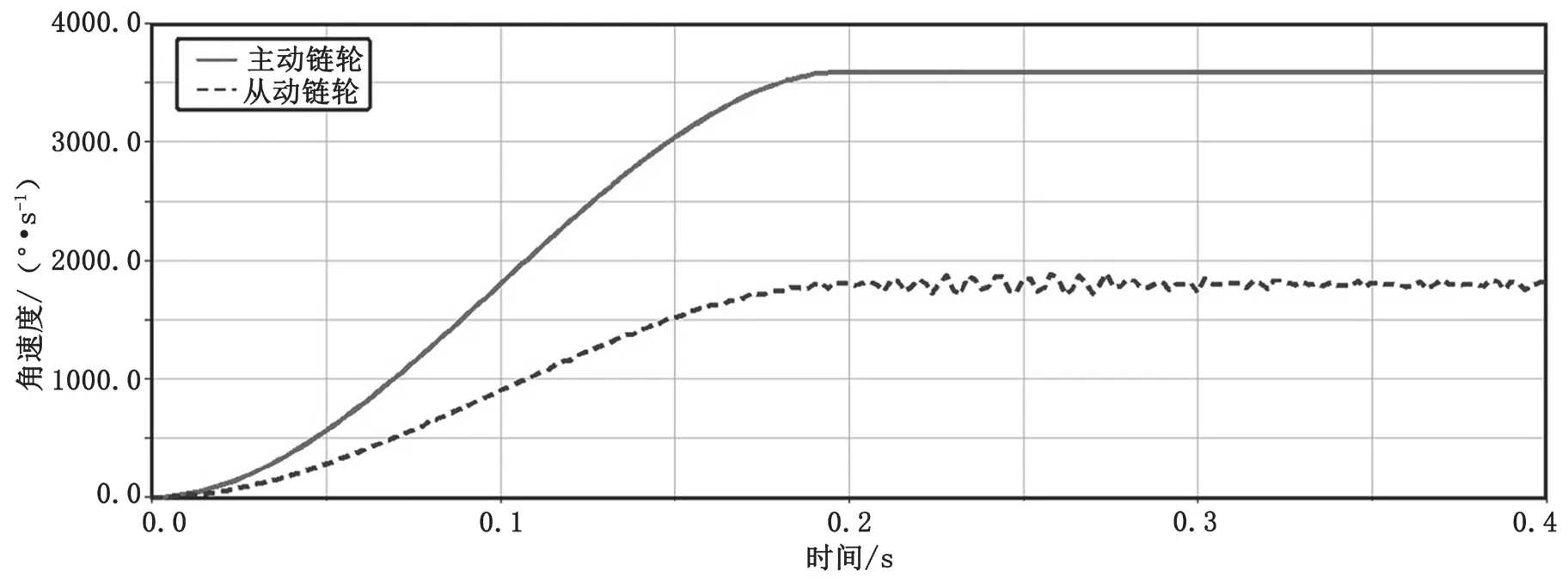
图3 主动轮与从动轮角速度曲线

从图4可以看出，主动链轮经过一个加速度由大到小的加速过程，角速度加速到3 600 °·s-1，而后保持平稳运行。加速度曲线呈正弦波形，此时链节传动速度如图5所示，传动速度在1 500 mm·s-1上下波动。图6和图7是在链系统运动过程中，主动链轮与从动链轮应力曲线变化。可以看出，两者受力情况相近。由于多边形效应，在运动过程中链条链节会在中心线部位上下波动，造成横向振动[5]。运动速度较快时，波动剧烈，造成较大的动载荷，使链轮应力曲线存在个别峰值。分析主动链轮受到的支反力，其中在X轴方向所受载荷最大，峰值在1 250 N左右；在Y轴方向正负载荷均存在，且交替出现，主要原因是链传动系统由于多边形效应造成运动不均匀性，使链上下波动，引起载荷在Y轴方向的正负交替变化；在Z轴方向受力为零，与实际分析相符。

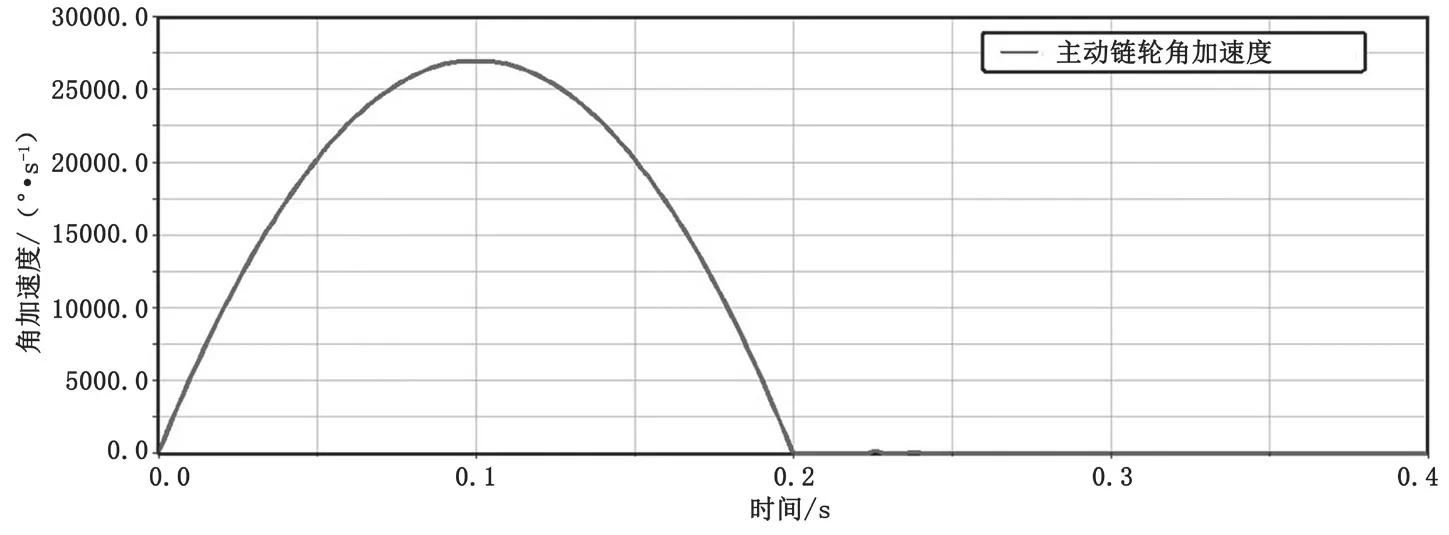
图4 主动轮角加速度曲线

图5 链节传动速度

图6 主动链轮受力

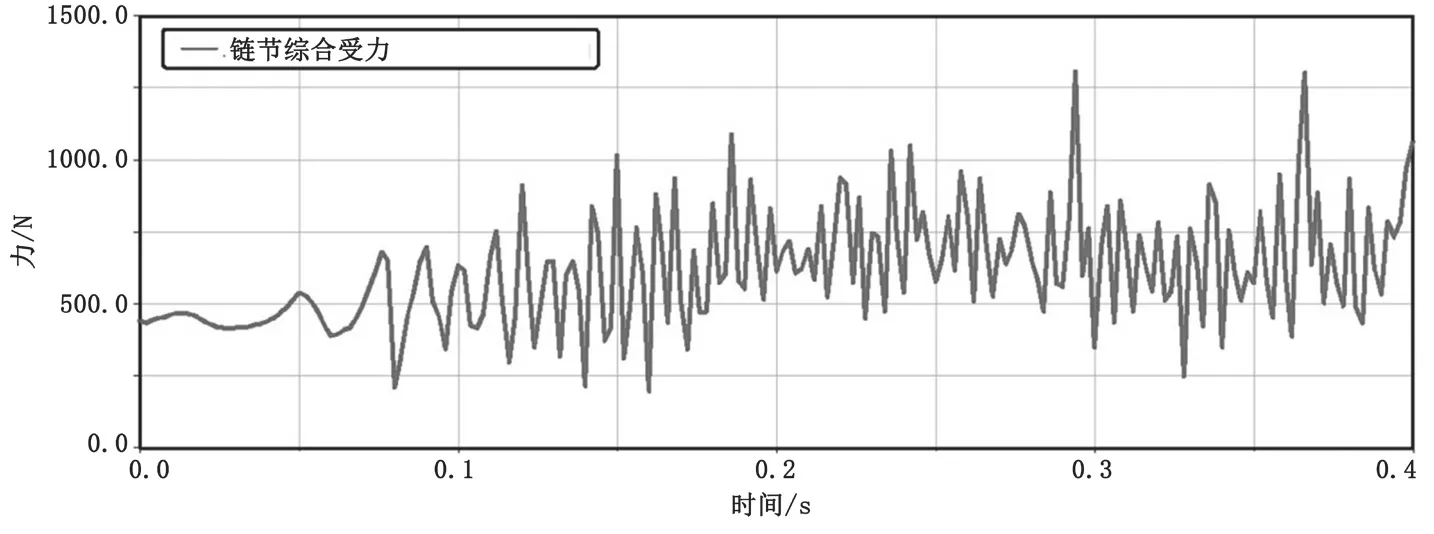
图7 从动链轮受力

2.3 不同磨损状态的链轮对链系统的影响

为了分析链轮在不同磨损状态下对链传动系统的影响，对链轮齿廓进行修改，如图8所示，并对不同状态链轮下的链系统进行仿真分析。如图8所示，实线为正常齿廓形状，虚线为磨损后齿廓形状，D为齿顶轮廓磨损尺寸。D为0.05 mm和0.10 mm时，主动链轮受力分别如图9和图10所示。D为0 mm、0.05 mm和0.1 mm时的齿廓链节受力，如图11所示。

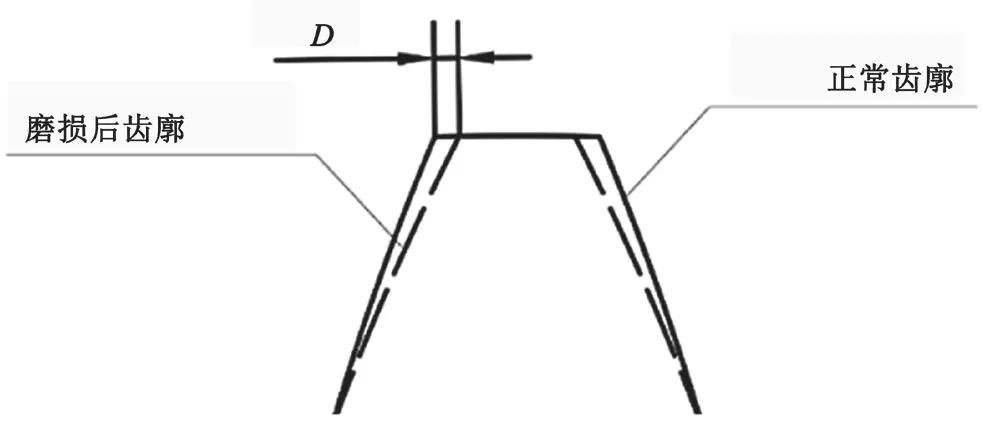
图8 正常齿廓与磨损齿廓对比示意图

图9 D=0.05 mm时主动链轮受力

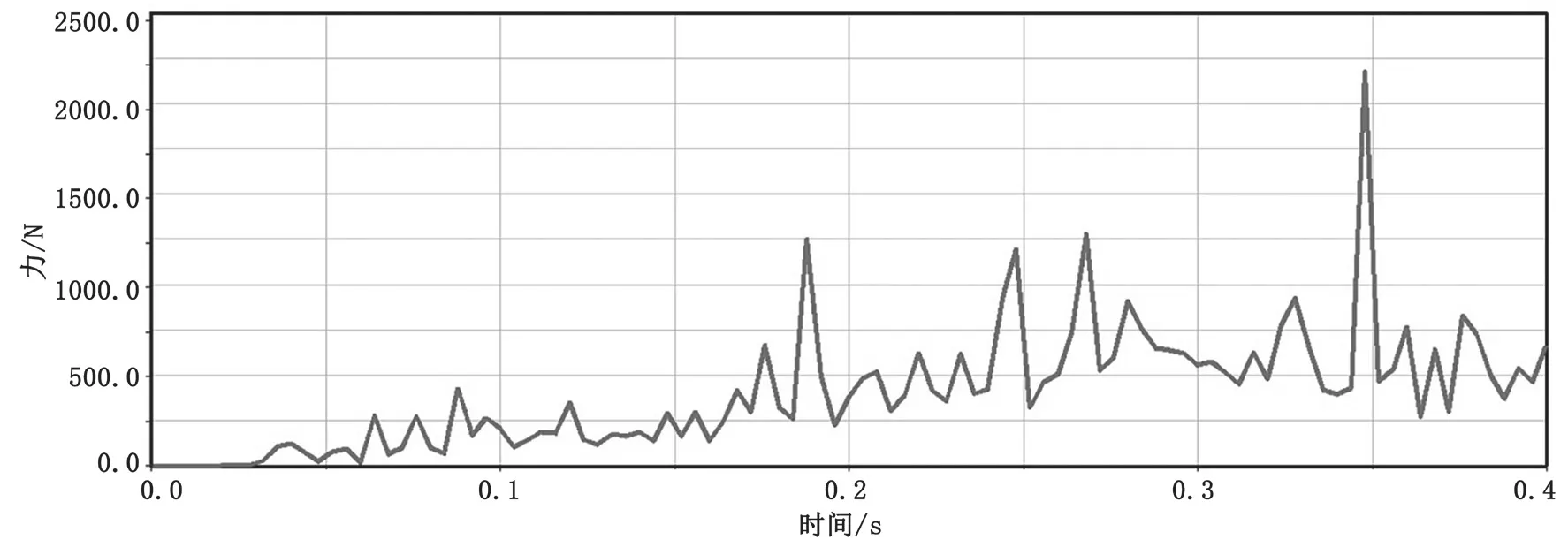
图10 D=0.1 mm时主动链轮受力

图11 不同D下的齿廓链节受力

链轮正常齿形受力情况下，综合受力峰值在1 250 N左右，在X轴上所受载荷峰值在1 500 N左右，Y轴上的载荷在-100～100 N波动；当磨损0.05 mm后的齿形特征输入后，综合受力峰值明显增大，在2 000 N左右，X轴上所受载荷峰值在2 000 N左右，Y轴上的载荷在-250～100 N波动；当磨损0.10 mm后的齿形特征输入后，综合受力峰值进一步增大，达到2 250 N，X轴上的所受载荷峰值在2 250 N左右，而Y轴上的载荷在-75～200 N波动。根据以上受力情况分析可以发现，随着链轮磨损的加重，链轮所受到的最大支反力逐渐增大，力变化曲线波动范围增大，波动明显加剧。发生上述变化的原因主要是链轮齿廓的磨损会导致链轮与链条的啮合位置发生改变，造成链轮与链条啮合过程中相对滑动趋势明显增大，使链系统运动不平稳性增加，波动逐渐加剧，链传动震动和噪声会明显增强。当波动进一步加剧时，会导致链节与链轮啮合时的瞬时加速度过大，导致跳齿，甚至链条脱落。对链节受力进行分析，也可以验证上述分析。随着磨损的加重，链节受力明显增大，由最大900 N变为1 200 N，再到3 500 N。更大的力会造成更大的加速度，加剧链节的波动，导致链传动系统的不平稳性，使传动效率下降，甚至系统失效。