电流互感器饱和后的二次侧电流有效值分析

朱忠亭，高 晶

(中国电力工程顾问集团华东电力设计院有限公司，上海 200063)

0 引言

电流互感器原理上与变压器类似，当一次侧电流远大于额定电流时可能会出现磁路饱和，此时电流互感器无法按照额定变比将一次侧电流转换为二次侧电流，从而可能对二次侧保护设备产生不利影响。为解决电流互感器饱和对保护设备动作的影响，一般可采取两类措施：一是选择抗饱和的电流互感器，当一次侧电流远大于额定电流时磁路仍然处于线性区域内；二是保护装置采取减轻饱和影响的措施，保证电流互感器在特定饱和条件下不致影响保护性能。

抗饱和的电流互感器成本较高、体积较大，一般只用于电压等级较高的重要电力系统中；而在普通的中、低压电力系统中，仍广泛采用易饱和的电流互感器。在同样的一次侧电流及不同的电流互感器情况下，饱和的电流互感器二次侧电流有效值显然应小于未饱和的电流互感器二次侧电流有效值；在同一个的电流互感器而不同的一次侧电流情况下，要确定饱和后电流互感器二次侧电流有效值与未饱和的电流互感器二次侧电流有效值的大小关系，必须对饱和后电流互感器二次侧电流有效值进行定量分析，这对于过流类有效值保护装置具有重要意义。

在不考虑非周期分量情况下，通过分析铁芯的饱和特性、研究电流互感器饱和时二次侧电流的波形，可以得出二次侧电流有效值的计算公式，再通过与电流互感器未饱和时二次侧电流有效值进行比较，即可得到两者的大小关系，从而可以判断电流互感器饱和是否会对过流类有效值保护装置产生影响。

1 饱和特性分析

为使铁芯得到充分利用，电流互感器额定运行点的磁通最大值往往已经处于铁芯的饱和段，主磁通φ与励磁电流If的关系呈饱和特性[1]，如图1(a)所示。铁芯磁路除了饱和以外，还有磁滞作用。它的磁化曲线不是单一的，上升和下降特性不相重合，形成了一个磁滞回环，如图1(b)所示。

为简化分析，假定电流互感器的磁化特性为阶跃函数。这里有两个简化，一个是将略有上涨的饱和线简化成完全的水平线；二是假定不饱和时铁芯材料的磁导系数为无穷大，即忽略了电流的励磁分量。在两个假设条件下，磁化曲线如图1(c)所示。鉴于磁滞作用只是改变一次侧电流和二次侧电流之间的相位关系，并不改变其比值关系，所以在计算二次侧电流有效值时，可以不考虑磁滞作用的影响，磁化曲线如图1(d)所示，后续分析及研究中均采用此种简化后的磁化曲线。

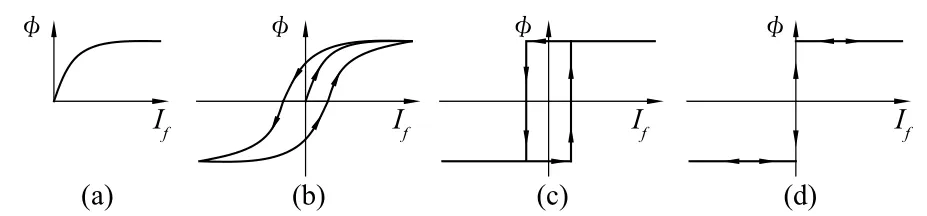
图1 磁化曲线

2 饱和前后有效值计算及比较

电流互感器的等值电路如图2所示，i1为一次侧电流，i2为二次侧电流，e2为二次侧电动势，R为二次侧等值电阻。分析计算中均不考虑非周期分量。

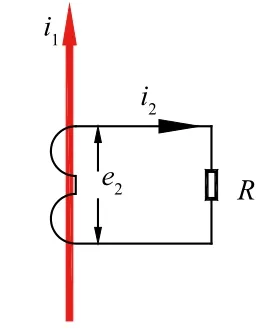
图2 电流互感器等值电路图

下面将根据图2等值电路，对电流互感器饱和前、饱和后进行分析，并对比相应的有效值。

2.1 饱和前

电流互感器在饱和前，二次侧电流随一次侧电流的增长而增长，是以额定变比为系数的线性比例关系，故电流互感器临界饱和时的二次侧电流有效值为饱和前的最大值。在图3中，i1、i2及φ分别代表电流互感器临界饱和时的一次侧电流、二次侧电流及磁通的波形。在0°～180°的半个周期内，i2为正，e2=i2R也为正。由于，故为负，磁通φ不断减小，至180°时为负的最大值，即为负的饱和值。

2.2 饱和后

若一次侧电流i1'增大为i1的K倍，即，如果磁通不饱和，则磁通的波形如图3中φ'所示，但实际上第一个周期内只有在90°-δ～90°+δ和 270°-δ～270°+δ范围时磁通才会处于不饱和状态，其他时间磁通均为饱和状态，实际的磁通波形如如图3中φ''所示。δ的数值取决于K，K较大时δ较小，反之亦然。根据前面的假定条件，磁通达到饱和以后即维持不变，于是，e2' =0，i2' =0，由于二次电流为零，一次电流全部成为励磁电流，一直维持φ''为饱和值。同样，根据前面的假定条件，在未达到饱和时励磁分量可以略去不计。在 90°-δ～90°+δ范围时，在 270°-δ～270°+δ范围时，。二次电流i'2的波形如图3中所示。

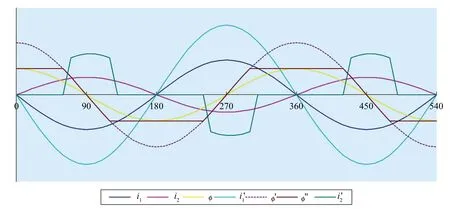
图3 电流和磁通波形

i2，e2及φ，e2之间的关系如式(1)和式(2)：

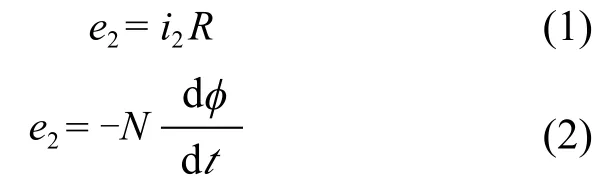
式中N为电流互感器二次绕组的匝数。

假设i2=Imsinϖt，根据式(1)和式(2)可得式(3)：

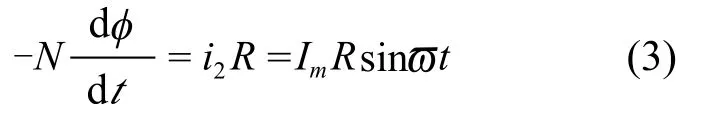
在临界饱和时，ϖt从0°变化到180°，φ从φm变化到-φm，可得式(4)和式(5)：

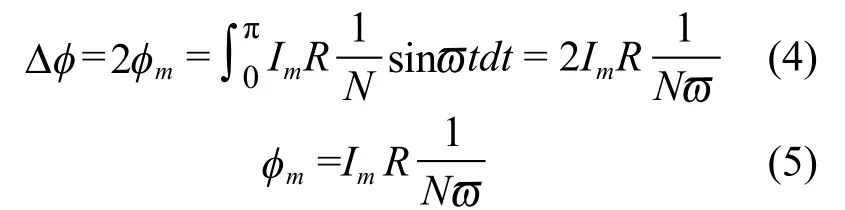
当一次侧电流增大K倍时，ϖt从90°-δ变化到 90°+δ，φ的变化量也是 2φm，可得式 (6)和式(7)：

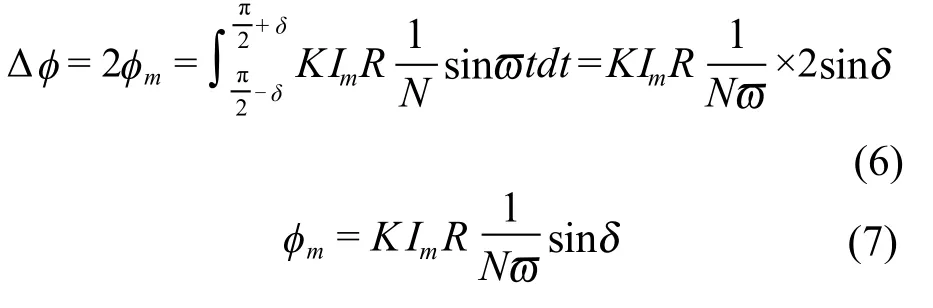
根据式(5)和式(7)，可得式(8)：

在电流互感器饱和以后，一次侧电流i1'=Ki1，二次侧电流的有效值为式(9)：

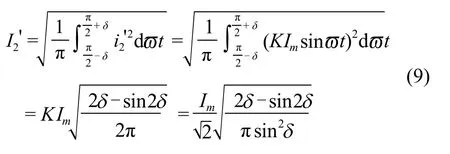
在电流互感器临界饱和时，二次侧电流为正弦函数，有效值为式(10)：

2.3 饱和前后对比

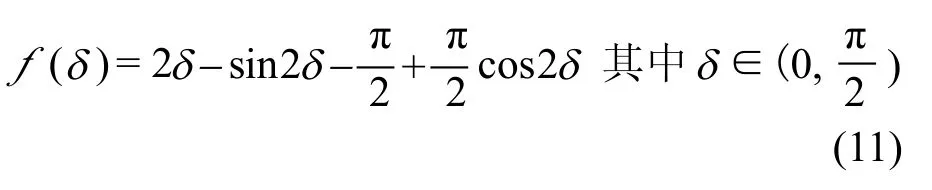
再设：

则式(11)可转化为式(13)：

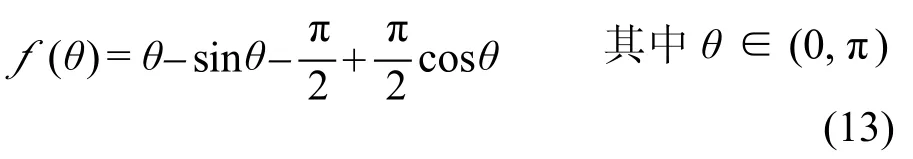
f(θ)函数曲线如图4所示。

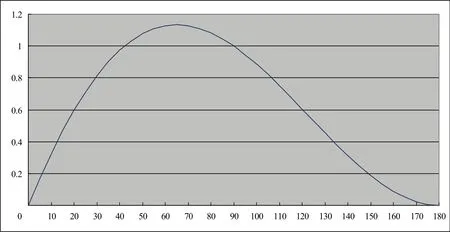
图4 f(θ)函数曲线

从图 4中可以看出，在θ∈(0, π)内，f(θ)＞0；即在内，f(δ)＞0。

可得式(14)和式(15)：

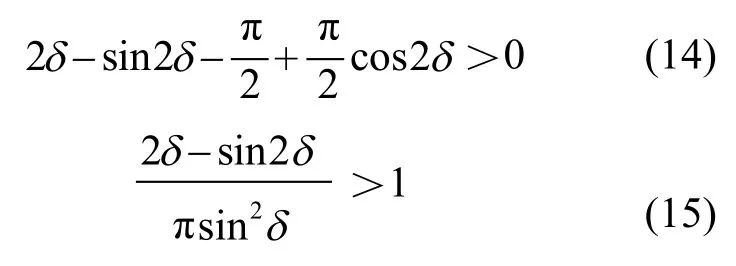
汇总式(9)、式(10)和式(15)，可得出结论：I'2＞I2，即在不考虑非周期分量情况下，电流互感器饱和时二次侧电流有效值总是大于临界饱和时的电流有效值，也大于未饱和时的电流有效值。当然，图4中的曲线均对应于理论计算值，在铁芯饱和后电流波形将严重畸变，而且分散性很大，保护装置内计算用电流值实际还受采样频率的影响。只有采样频率满足准确获得二次侧电流有效值的要求时，保护装置才能适用上述“饱和值总是大于未饱和值”的结论。

3 结语

随着电流互感器一次侧电流的增加，在铁芯达到饱和前，二次侧电流按照变比线性增加；在铁芯达到饱和后，二次侧电流虽然无法按照变比线性增加，但通过定量分析计算可知，其有效值仍然大于未饱和时的有效值。因此，对于过流类有效值保护装置，在其采样频率满足准确获得二次侧电流有效值要求的条件下，如果铁芯不饱和时能正确动作，则在铁芯饱和后仍能正确动作。