基于柔性神经元的煤矿安全风险预警模型研究
2021-07-27陈佳林付恩三
陈佳林,付恩三
(应急管理部信息研究院,北京 100029)
为进一步强化煤矿企业本质安全水平,提升企业对煤矿企业安全风险的预测预警能力,提高安全生产监管监察水平,本文以人工智能技术为基础,基于连续值逻辑的健全性,连续值逻辑把M-P神经元模型扩张为连续值神经元,通过多源柔性神经网络[1,2]多维度、多视角、全方位对煤矿各类主要在线监控数据,安全生产规章制度、技术管理制度,安全风险管控、隐患管理治理等过程数据进行训练,建立煤矿风险预警指标体系指标因子的属性关系网络和连续值逻辑柔性算子库,提取隐含的规律和有用信息,构建基于柔性神经元决策树算子模型,实现煤矿风险的分析研判和实时预警,为日常监察、远程联网分析、执法检查和应急救援等工作提供数据支撑和技术手段[3-5]。
1 连续值逻辑谱与健全性
随着人工智能领域的不断发展,人们在实际的应用中发现,很多的非标准逻辑中,标准逻辑的一些重要性质发生了变化。很多专家通过验证,信息传输和使用中,信息在处理过程中发生了畸变,因此,很多非标准逻辑虽然具有“可靠性”和“完备性”,它们的逻辑推理失去了“可信性”,专家通过引入不确定性因素,形成了多组逻辑组成一个逻辑系统,不同应用条件对应不同逻辑算子,连续值逻辑演变成逻辑谱,从逻辑谱的角度利用连续值逻辑代数完善现有的各种柔性逻辑命题逻辑系统[4]。
1.1 健全逻辑的基本性质
在信息处理的过程中,要遵循相应的逻辑规律,其中,逻辑规律包含一些数学规律。可以设定,逻辑中的命题P是信息的一种抽象表示,通过多种多样的逻辑表达式描述不同信息的复杂构成,逻辑的推理过程可以表述信息的变化过程。通常使用的标准逻辑的基本性质反映了信息结构和信息运动的基本规律,它满足了健全的逻辑系统必须具有的基本性质[5,6]:
(L1)P∨P=P信息(命题)不会因为被无限多的分享而发生改变。
(L2)P∧P=P信息(命题)不会因为多次地重复而改变。
L1和L2统称为吸收律或幂等律。
(L3)~P∧P=0矛盾律。
(L4)~P∨P=1排中律。
(L5)~~P=P对合律。
(L6)P,P→Q|=QMP规则。
逻辑是信息世界的基本法则。具有基本性质L6的系统为逻辑系统。如果一个逻辑系统具有全部的基本性质L1、L2、L3、L4和L5,则称为健全的逻辑系统;否则称为非健全的逻辑系统。
1.2 连续值逻辑的健全性
连续值逻辑中存在5种不确定性[7-9]:①基于命题真度的不确定性x,y,z∈[0,1];②基于命题之间广义相关关系的不确定性h∈[0,1];③基于命题真度误差的不确定性k∈[0,1];④基于不同权重的不确定性β∈[0,1];⑤基于组合阈值的不确定性e∈[0,1]。
连续值逻辑非运算的基模型是N(x,k)=N(x,0.5)=N(x),组合运算的基模型是Ce(x,y,k,h,β)=C0.5(x,y,0.5,0.5,0.5)=C0.5(x,y),其它各种柔性二元运算的基模型是L(x,y,k,h,β)=L(x,y,0.5,0.5,0.5)=L(x,y)。常用的基模型有:
非运算基模型N(x)=1-x
与运算基模型T(x,y)=max(0,x+y-1)
或运算基模型S(x,y)=N(T(N(x),N(y)))=min(1,x+y)
蕴涵运算基模型I(x,y)=max(z|y≥T(x,z))=min(1,1-x+y)
等价运算基模型Q(x,y)=T(I(x,y),I(y,x))=1-|x-y|
平均运算基模型M(x,y)=N(S(N(x)/2,N(y)/2))=(x+y)/2
组合运算基模型C0.5(x,y)=ite{min(0.5,max(0,x+y-0.5))|x+y<1;
N(min(N(0.5),max(0,N(x)+N(y)-N(0.5))))|x+y>1;0.5}
=min(1,max(0,x+y-0.5))
其中e∈[0,1]是表示弃权的幺元(决策阈值),ite{y|x;z}是条件表达式,意思是“如果x,则y;否则z”。
1)通过对N性生成元完整簇Φ(x,k) =xn,n∈(0,∞),n=-1/log2k完成对误差系数k连续变化对连续值逻辑基础运算模型的调整,Φ(x,k)对一元运算基模型N(x)调整公式为N(x,k) =Φ-1(1-Φ(x,k),k) = (1-xn)1/n,Φ(x,k)对二元运算基模型L(x,y,k) 调整公式为L(x,y,k)=Φ-1(L(Φ(x,k),Φ(y,k)),k)。
2)通过对T性生成元完整簇F(x,h)=xm,m∈(-∞,∞)上,m=(3-4h)/(4h(1-h))完成命题的广义相关系数h的连续变化对逻辑运算模型的调整。F(x,h)对各种二元运算基模型L(x,y)的运算公式是L(x,y,h)=F-1(L(F(x,h),F(y,h)),h),k,h二者对二元运算基模型L(x,y)双参数运算公式是L(x,y,k,h)=Φ-1(F-1(L(F(Φ(x,k),h),F(Φ(y,k),h),h),k)。
3)通过完成相对权系数β的连续变化对二元运算基模型L(x,y)的运算公式是L(x,y,β)=L(βx,(1-β)y),k,h,β三者对二元运算模型L(x,y)多参数运算公式是L(x,y,k,h,β)=Φ-1(F-1(L(βF(Φ(x,k),h),(1-β)F(Φ(y,k),h),h),k)。
误差系数是不确定性推理密码串
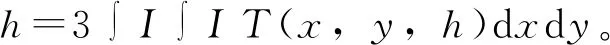
偏袒系数是不确定性推理密码串
组合运算模型中的决策阈值e是不确定性推理密码串
2 柔性神经元的
2.1 柔性神经元模型
通过理论证明,基于连续值逻辑的健全型基模型,可以验证神经元信息变换模式与逻辑推理模式有一一对应的关系[8,9],连续值逻辑把M-P神经元模型扩张为连续值神经元(相当于基模型状态),然后再引入基于命题真度的不确定性、基于命题之间广义相关关系的不确定性、基于命题真度误差的不确定性、基于不同权重的不确定性和基于组合阈值的不确定性等多种不确定性,扩张为柔性神经元模型(详细如图1所示)。
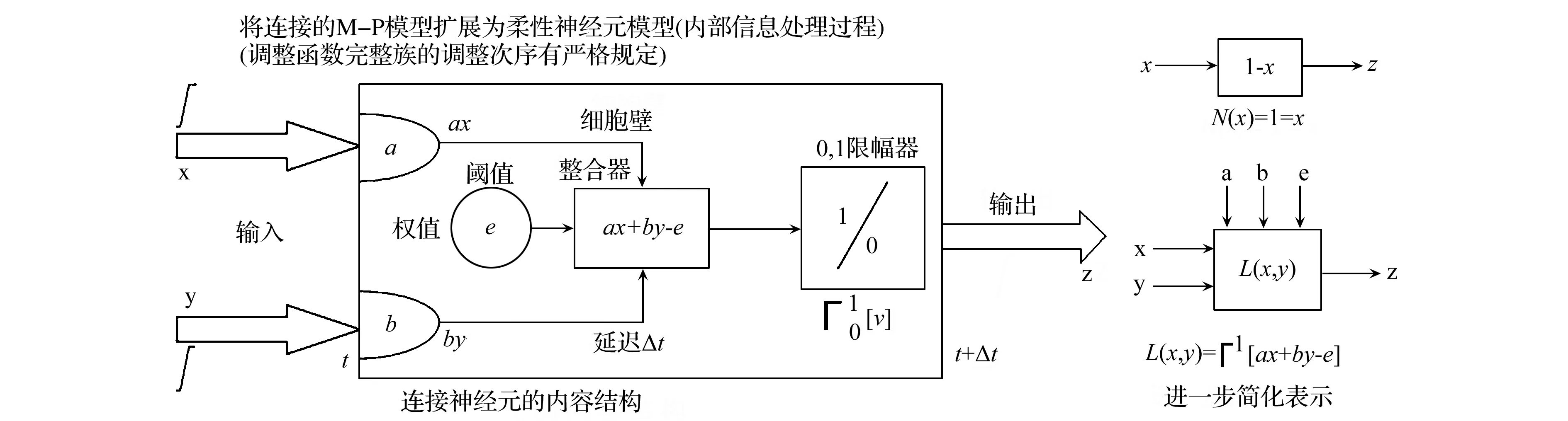
图1 柔性神经元模型
已知待识别对象的实测数据集合S’={s’i|i=0,1,2,3,…,n},对这些数据进行统计分析和知识挖掘,可获得对象可能具有的因素空间关系网络W’={w’i|i=0,1,2,3,…,n},其中每一个w’i都是一个柔性逻辑推理结点或者柔性信息变换的神经元,具有相应的类型参数
在指标体系的构建方面,选取内蒙古井工煤矿的指标体系,人机环管的方面考虑较多,将煤矿静态指标、动态指标以及历史事故指标纳入其中。包含人的因素(学历占比、工龄占比、年龄占比、培训率、持证率、井下领导、超员次数、三违次数、超时次数等9项),环境因素(气象风险指数、水害风险指数、顶板风险指数、瓦斯风险指数、火灾风险指数、煤尘风险指数),管理因素(安全经费、月产量、标准化等级、通风隐患整改率、地质灾害防治与测量隐患整改率、采煤隐患整改率、掘进隐患整改率、机电隐患整改率、运输隐患整改率、职业卫生隐患整改率、安全培训和应急管理隐患整改率、调度和地面设施隐患整改率、月度重大风险检查、月度标准化自查结果、井下重点部位隐患排查、行政处罚次数、是否存在重大违规),井工矿设备因素(大型在用设备检验合格率、送检设备合格率、人员定位系统运行状况、瓦斯监控系统运行状况、视频监控系统运行状况、矿压监测系统运行状况、水文监测系统运行状况、压风系统运行状况、无轨胶轮车监控系统运行状况),共4类一级指标,40个二级指标,93个三级指标[10-15]。
选取内蒙古煤矿小鱼沟煤矿、呼和乌素煤矿等27家煤矿的20000条历史数据构成实测数据集合S’,指标体系指标因子关系网络集合W’初始情况随机赋值,利用神经网络训练不断调整关系网络集合W’,使实测数据集合S’无限接近真实集合S。经过多次循环验证,获取关系网络集合W,从而获得每一个wi,确定每一个神经元的属性
2.2 算法与实验分析
获取到每个神经元的属性值,就可以根据属性关系,利用柔性组合算子模型,选择合适的算子,本文采用柔性神经元算子模型算法。
设x1,x2,…xn表示输入变量,β1,β2,…βn表示输入变量的权值,h表示输入变量的广义相关系数,e仍然是组合运算中的幺元,c表示运算结果。
G(x1,x2,…xn,h,e,β1,β2,…βn)
{
ifh=1
{c=ite{min(x1,x2,…xn) |β1x1+β2x2+…+βnxn
else ifh=0.75
{c=ite{x1β1x2β2…xnβn/en-1|β1x1+β2x2+…+βnxn
else ifh=0.5
{c=min(1,max(0,β1x1+β2x2+…+βnxn-(n-1)e));}
else ifh=0
{c=ite{0 |x1,x2,…xn
else
{m=(3-4h)/(4h(1-h));
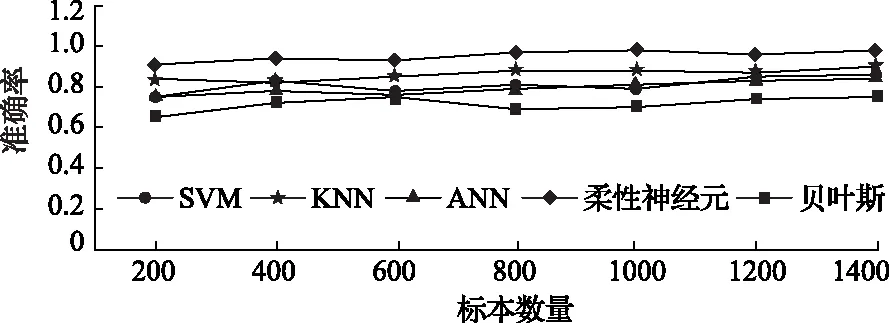
c=ite{min(e,(max(0,β1x1m+β2x2m+…+βnxnm-(n-1)em))1/m) ite{min(x1,x2,…xn) |β1x1+β2x2+…+βnxn β1x1+β2x2+…+βnxn>ne;e}|β1x1+β2x2+…+βnxn Return(c); } 构建决策树的匹配过程,其匹配结果依赖于基于柔性神经元所选的推理算子。对已产生的柔性神经元算子模型进行匹配的算法如下图所示。首先对测试数据进行模糊化,得到的模糊数据进行匹配,匹配过程如图2所示,最后对得到的测试精度进行比较研究。 图2 算法流程图 通过利用基于20000条历史数据训练获取的指标体系指标因子关系网络,利用柔性神经元算子模型进行测试分类,并与传统的分类算法SVM(基于内核函数的无监督学习算法),KNN(最近邻分类算法),ANN(人工神经网络算法)和贝叶斯算法(概率统计知识分类算法)比较,如图3所示。 图3 各类算法分类比较图 通过上述数据模拟训练可知,根据小鱼沟煤矿、呼和乌素煤矿等27家煤矿的实际生产的指标体系,进行多次算法模型计算,得出煤矿风险评价结果。柔性神经元算子在风险预测准确率上具有较大的优势,柔性神经元法准确率高出其他算法将近20个百分点。结合专家对上述煤矿的风险信息解读风险权重影响因子及本模型风险研判的极高风险因素占比,该模型算法得出结果与专家评价具有较好的一致性。 为保证该模型的实用、好用、管用,实现对煤矿安全风险进行实时预警。同步开发一套煤矿风险预警与防控系统,将上述训练优化后的柔性算法模型,打包嵌入至该系统中。系统部署在煤矿端,每天定时调用柔性模型算法包,对煤矿进行综合风险实时巡查。通过该柔性算法模型的计算,可给出煤矿风险评价指标体系中四个一级指标的得分情况以及84个三级指标的权重及得分情况。当前煤矿实时风险分布及灾害信息。可摸清煤矿井下风险,知悉风险趋势。以小鱼沟煤矿风险预警系统为例:通过调用柔性指标模型,实现对煤矿的风险研判。 通过柔性模型研判结果可知,当前煤矿综合风险得分为74.86分,其中,煤尘风险、火灾风险、水害风险处于极高和较高风险的状态。系统根据模型打分结果,结合煤矿安全监控系统、束管监测系统、水文地质监测系统数据,发现当前煤矿井下煤尘浓度较高、井下水位/水文异常以及井下上隅角CO浓度超标。上述问题均是导致事故发生的异常风险点。柔性模型根据上述因子之间的风险程度关系和各类指标之间的相关联因素,给出不同风险因子的权重。上述各类风险信息等级,通过与煤矿总工程师、安全生产专员沟通后,认为柔性风险分析模型结果与煤矿当前面临的风险结果一致,该模型可实现对煤矿风险的实时预警,研判结果可靠。 柔性神经元网络有效的规避了模糊逻辑运算的最大最小刚性原则,通过考虑参数(属性)之间客观上存在的广义相关性及交互信息等信息,提供了一个选择匹配算子的准则。通过建立的基于柔性神经网络模型,指标体系相关数据的检验分析表明,基于柔性神经元网络的决策树风险预警模型算法,能够较充分的反应煤矿企业安全风险,分类效果显著,有助于企业安全风险的预测预警能力率。对于煤矿安全风险预警分析模型需要说明几点: 1)基于柔性神经元的煤矿安全风险预警模型应用到内蒙古小鱼沟煤矿,目前已经运行半年时间,系统模型研判结果与煤矿识别风险结果基本保持一致。该算法有一定的应用价值,为煤矿安全生产预警和决策提供重要的理论依据。 2)煤矿安全风险预警模型的构建,是一个长期的过程,需要充分结合煤矿安全生产业务系统中所涉及的关键指标,同时需要充分考虑指标体系的数据可获得性,根据煤矿的特点,逐步优化指标体系、逐步训练优化分析模型,充分与煤矿安全管理人员进行模型风险辨识校对,最终实现模型的落地应用。 3)在今后的研究中,将不断的优化指标模型,通过获取不同矿山数据,逐步完善风险预警模型,最终形成模型适用条件、适用场景以及适用煤矿,逐步积累,形成一矿一策的预警模型。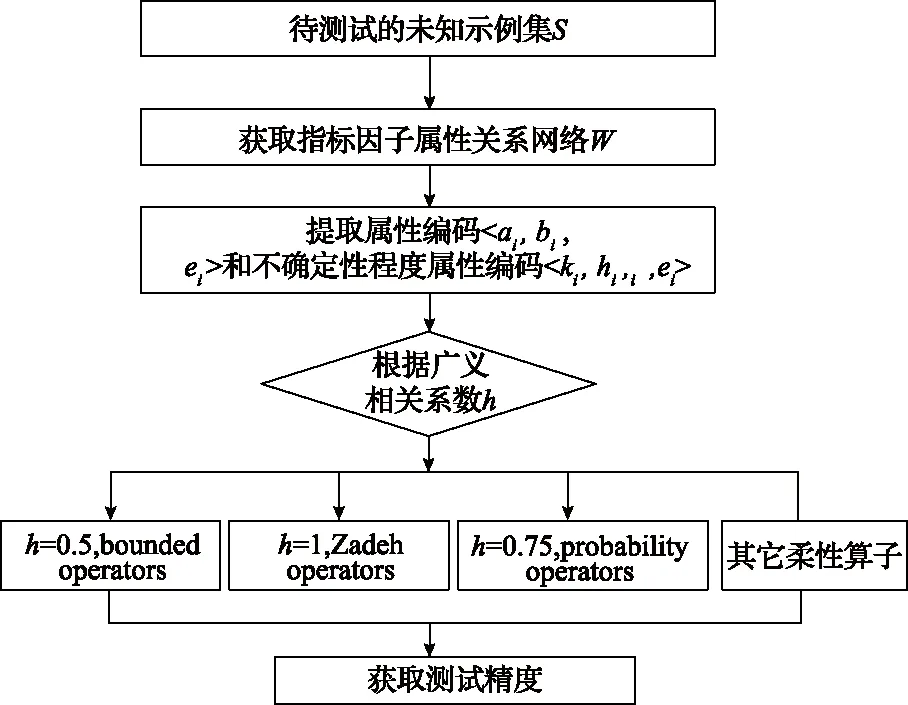
3 实例研究
4 结 论
