高速列车牵引电机自适应故障诊断研究
2021-07-27申欣艳
谭 畅,申欣艳,杨 辉
(1.华东交通大学电气与自动化工程学院,江西 南昌 330013;2.华东交通大学江西省先进控制与优化重点实验室,江西 南昌 330013)
高速列车凭借其速度快、运量大等优点成为越来越多人出行的选择[1-2]。 作为保障列车安全准点运行的重要组成部分,列车牵引系统受到学者的广泛关注,其中,牵引电机是列车牵引系统中动力单元的核心部件。 在高速列车运行期间,牵引电机可能因为长时间工作或者自然气候的腐蚀, 导致其老化、磨损而发生故障。 这些故障会产生非正常的牵引力,使列车不能按预期的设定运行,甚至失控而引发事故[3-5]。 开展对高速列车牵引电机故障诊断与调节的研究具有重要的理论和实际意义。
为了保障高速列车安全运行,姜斌[6],张振宇[7],程海鹏[8]等为这方面研究提供了理论基础。 Tao 等[9]和Tan 等[10]从理论角度提出了用冗余执行器解决执行器故障调节问题,分别采用直接自适应和间接自适应故障调节的方法。 罗茹丹等[11]以高速磁浮列车为对象,对其电机进行建模,从电磁场角度分析故障。 马杰等[12]和陈哲明等[13]以高速动车组为研究对象,分别从牵引电机的定子匝间短路和转子振动两方面分析, 通过故障对动车组的影响进行诊断研究。 丁小健等[14]分析了单相交流电机常见的4 种故障状态,用小波降噪方法进行试验。杨超等[15]从故障输入、仿真可信度评估、算法性能评估和仿真平台等方法进行分析,对列车牵引传动系统的故障检测问题提出解决方案。 Zhang 等[16]对高速列车制动系统传感器故障提出一种基于滑模观测器的诊断方法。 Lin 等[17]针对高速列车执行器发生故障,同时受到外界干扰的条件下,用一种基于滑模技术的神经自适应控制方法。 Tao 等[18]从设计控制器方面入手,提出了故障检测、 故障隔离和模型预测控制的方法,对高速列车容错控制做出重要贡献。 Wang 等[19]针对高速列车动态系统的跟踪问题,借助广义参数估计误差,提出一种分布式容错控制方案。 Yin 等[20]运用深度学习的方法与人工神经网络方法对比,设计了较准确的高速列车的自诊断方案。Bai 等[21]设计了高速列车动力学故障检测滤波器,用来解决基于耦合器的非线性动力学特性建模问题。 Mao 等[22]考虑到因时变摩擦特性引起的列车动力学参数的变化,提出适用于具有可变参数的动力学模型的一种新的分段常数模型,设计自适应律更新控制器参数达到渐近跟踪。 虽然国内外专家学者在理论与实际方面做出了很多贡献,但现有的成果要么是针对牵引电机内部零件故障对电机建模,分析对电机造成的影响,未与列车运行相结合;要么从列车牵引力角度诊断故障,在实际中不方便操控。
本文的主要创新点包括:结合列车牵引力特性和列车运行特点,将多模型自适应的方法用于牵引电机的故障诊断和调节,利用多个估计器,实现了对未知牵引电机故障的快速准确诊断;将自适应善于处理被控对象不确定性的优势用于高速列车故障诊断和速度跟踪控制,使其在系统和故障不确定性的情况下, 仍能实现对给定速度曲线的渐近跟踪,保障高速列车的安全可靠运行。
1 存在牵引电机故障的高速列车动力学模型
为了研究高速列车牵引电机自适应故障诊断和调节方法,建立高速列车纵向动力学模型和牵引电机故障模型,推导出存在牵引电机故障的高速列车动力学模型,并提出控制目标。
1.1 高速列车纵向运动学模型
为研究方便,将高速列车看作一个刚体,建立其单质点运动学方程为

式中:M 为列车质量;x¨(t)为列车运行加速度;F(t)为列车所受的牵引力;Fr(t)为基本阻力;Fg(t)为坡道阻力;Fc(t)为弯道阻力;Fg(t)与Fc(t)合称附加阻力。 为了建立高速列车动力学模型,接下来进一步对F(t),Fr(t),Fg(t)和Fc(t)进行分析。
牵引力:高速列车的牵引力由牵引系统的执行机构,如牵引电机、机械传动机构以及脉冲宽度调制器(pulse width modulations,PWMs)等产生。 为了设计简单,本文仅考虑牵引电机产生的影响,并将电流作为系统的控制输入,与经典控制理论中的表达形式一致,用u(t)表示。 根据文献[23]中列车牵引力与电流之间的非线性关系,可近似拟合为

式中:n1,n2均为拟合系数。
基本阻力:基本阻力是指零部件之间、列车表面与空气之间、 车轮与钢轨之间的摩擦力和冲击力。 参考文献[24],将基本阻力Fr(t)定义为
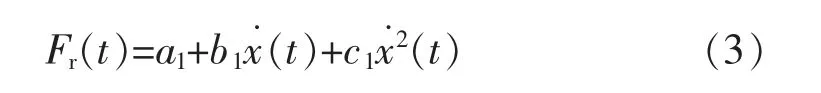
式中:a1,b1,c1为基本阻力系数,与列车车型、运行环境有关;x˙(t)为列车运行速度。
坡道阻力:坡道阻力由列车运行当前的轨道倾斜角决定,参考文献[24]。 将其表示为

式 (7) 为本文建立的高速列车纵向动力学模型。 接下来本文将以该模型为基础推导存在牵引电机故障的高速列车模型。
1.2 存在牵引电机故障的高速列车模型
通过对高速列车常见的牵引电机故障进行分析,推导其故障模型,建立存在牵引电机故障的高速列车动力学模型。
常见的牵引电机故障有定子故障、转子故障以及轴承故障。 定子故障主要为定子匝间短路,转子故障主要为转子断条和断裂,轴承故障主要为内圈故障、外圈故障与滚动体故障[7]。 定子或转子发生故障时,由于定子转子之间存在的耦合关系,电流呈周期变化[13],建立故障模型为
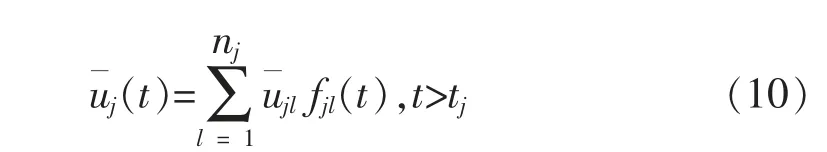
式中:ujl为未知常数;j 为牵引电机编号;tj为发生故障的时刻;fjl(t)为已知基函数,一般选取正弦或余弦函数;nj为基函数的个数。 大部分牵引电机出现故障后的参数化模型可以通过选择适当的基函数fjl(t)逼近实际故障,并通过ujl参数化,尤其是只要nj足够大,选择的基函数足够多,就可以使参数化故障模型逼近实际故障。 另外,当电机过热或电机转子卡住时, 电机将会停止运行来保护系统安全,其故障模型可表示为

在存在牵引电机故障的情况下,具有4 个牵引电机的高速列车的输入信号为

得到存在牵引电机故障的高速列车纵向动力学模型为

上述模型的输入信号由控制信号v0(t)和故障信号v(t)组成,共同作用于高速列车牵引系统。 当高速列车所有牵引电机正常工作时,各个电机按照式(14)提供不同大小的牵引力;当某几个电机出现故障,由剩余的健康电机提供牵引力,使高速列车仍能跟踪给定的速度曲线。
1.3 控制目标
针对存在未知牵引电机故障式(16),设计自适应故障诊断策略,确定发生故障的电机和其故障大小,并根据诊断结果设计容错控制器,使其在发生未知牵引电机故障后不但能保证系统稳定,且能实现对给定的速度曲线的渐近跟踪。
为了实现上述控制目标,根据熟练司机的驾驶经验设计理想的速度曲线xm2(t),据此计算理想的位移曲线xm1(t)。 为了设计自适应控制策略,本文选取稳定的参考模型
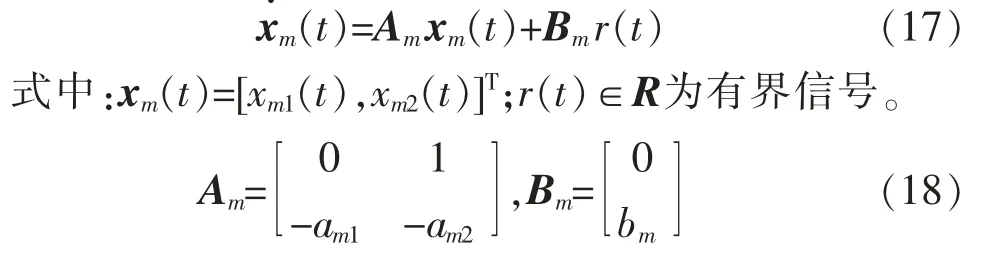
式中:am1>0,am2>0,bm>0 为设计参数, 其根据设计要求和实际的列车数据进行选择。
本文选择参考模型的方式区别于传统模型参考自适应控制(MRAC)方法,传统的MRAC 选择外部输入信号r(t),再根据具体跟踪选定参考模型(Am,Bm),产生参考模型的输出xm(t)作为系统输出x(t)跟踪的目标曲线,其主要体现了MRAC 对任意曲线的渐近跟踪能力。 本文在选择跟踪目标曲线和参考模型时,是根据司机的驾驶经验设计理想的速度曲线,即参考模型的输出xm2(t),计算得到xm1(t),再根据设计要求和列车数据选定参考模型 (Am,Bm),计算得到外部输入信号r(t),并将r(t)用于自适应控制器的设计实现对理想速度曲线的渐近跟踪。 本文选择参考模型的方式是根据具体控制问题对传统MRAC 的应用与发展。
2 高速列车自适应故障诊断与调节
为了实现对高速列车未知牵引电机故障的自适应诊断和调节, 对常见的牵引电机故障进行分析,定义故障模式集;然后推导高速列车在每种故障模式下的参数模型和自适应估计器;再基于估计误差设计性能损失函数,诊断高速列车发生故障的模式和大小;最后根据诊断结果设计故障调节控制器,使其在发生未知牵引电机故障时仍能实现对给定速度曲线的渐近跟踪。
2.1 故障模式集
为了研究方便, 将无故障的情况看作一种特殊的故障模式。 通过对高速列车牵引电机故障进行分析,定义包括如下4 种情况的故障模式集。
1) 无故障模式,即所有执行器正常工作;
2) 常值故障模式,牵引电机故障模型为式(11);
3) 时变故障模式,牵引电机故障模型为式(10);
4) 组合故障模式,牵引电机故障模型为式(12)。
为了推导高速列车在不同故障模式下的动力学模型,本文在式(15)的基础上进一步定义
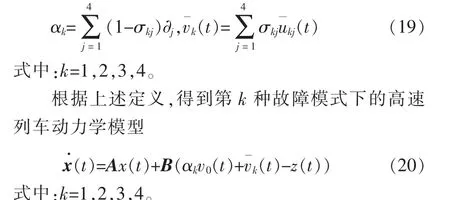
2.2 不同故障模式下的高速列车参数化模型
为了设计高速列车自适应故障诊断和调节策略,本节推导高速列车在不同故障模式下的参数化模型。 对于高速列车故障调节系统,有如下基本的匹配等式。

1) 无故障模式:ωk(t)=ω1(t)=1;
2) 常值故障模式:ωk(t)=ω2(t)=1;

2.3 基于多模型的自适应故障诊断

式中:P 为常值矩阵;η1=η1T>0;η2>0;η4=η4T>0;η3=η3T>0;P=PT>0。满足PAm+AmTP=-Q,Q=QT>0。不同故障模式下的参数值构成了自适应估计器参数的集合。 通过参数的更新可以得到所有参数值。
为了实现高速列车牵引电机自适应故障诊断,本文基于估计误差设计性能损失函数,通过性能损失函数判断与实际故障最匹配的估计器,从而诊断出实际发生的故障模式,即首先基于估计误差e(k)(t)定义每种故障模式下的性能损失函数
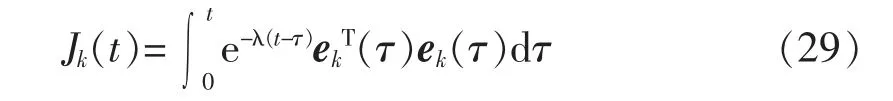
式中:k=1,2,3,4;常数λ>0;再找出与实际故障最匹配的估计器对应的故障模式,即对应性能损失函数最小的故障模式
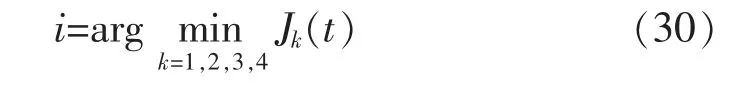
则第i 种故障模式即为本文设计的多模型自适应故障诊断策略诊断出的故障模式。 最后由第i 种故障模式下对应的参数值θ(i)3(t),得到发生故障的大小,由此完成故障诊断过程。
2.4 牵引电机故障调节
为了使高速列车能在发生未知牵引电机故障情况下仍能保持稳定,且能实现对给定速度曲线的跟踪, 本文依据诊断出的故障模式i 和故障大小信息θ(i)1,θ(i)2,θ(i)3,θ(i)4,设计这种故障模式下的故障补偿控制器,对故障进行调节,即

本文设计的高速列车牵引电机故障调节控制器v0(t),在存在未知牵引电机故障情况下能保证闭环系统所有信号有界,且当时间t→∞时,速度位移跟踪误差x(t)-xm(t)趋于零。
3 仿真验证
为了验证本文设计的自适应故障估计和调节策略的有效性, 本节以CRH 型高速列车为被控对象进行仿真验证,并与Zhang 等[16]和Lin 等[17]的方法对比,以验证该方法的优势。
根据文献[23],有M=106kg,D=0.34,θ=10°,a=1.66 kN/kg,b=0.007 5 (kN·s)/(m·kg),c=0.000 155(kN·s2)/(m·kg),n1= 0.640 6,n2=7.6。 选择参考模型参数为:am1=0.12,am2=1.9,bm=(500×103)-1。
基于前文对故障原因的分析,在仿真中,我们假设在70 s 处牵引电机发生了常值故障,160 s 处假设发生组合故障,即
1) 当t<70 s 时,4 个牵引电机正常工作;
2) 在70 s 时,牵引电机2 发生常值故障u2(t)=300 A;
3) 在160 s 时, 牵引电机2 发生常值故障,即u2(t)=300 A,牵引电机4 发生时变故障,即u4(t)=200sin(1+0.05t)A。
为了进行仿真,选择状态初始值x(0)=xm(0)=[0,0]T,选择参数初值为θ(k)j(0)=95%θ*(k)j,其中θ*(k)j为参数真值[23],θ*(k)1T=[-6 000,-9.5×105],θ*(k)2=0.640 6,θ*(k)3=0,θ*(k)4T=[-2.665×106,3.2×10-4];选择设计参数为η(k)1=1.2I,η(k)2=1,η(k)3=0.75I,η(k)4=2I,I 为单位矩阵。 设计高速列车牵引电机故障诊断和调节策略并用MATLAB进行仿真,得到的仿真结果如图1~图2 所示。
图1(a)反映了在70 s 之前故障诊断策略判断系统处于第1 种故障模式,即牵引电机正常工作,在70 s 和160 s 之间故障诊断策略判断系统处于第2 种故障模式,在160 s 后故障诊断策略判断系统处于第4种故障模式。 图1(b)和图1(c)可以看出自适应故障诊断方法有效地估计出了故障大小。 图1(b)反映了在70 s 处发生的常值故障模式下, 参数通过自适应律的更新对实际故障进行了估计;图1(c)反映了伴随着70 s 处发生的常值故障,高速列车在160 s 又发生一次故障时,本方案同样估计出了实际故障大小。

图1 高速列车自适应故障诊断效果Fig.1 High-speed train fault mode diagnosis and fault value estimation
图2(a)和图2(b)分别反映出位移跟踪误差和速度跟踪误差。 位移误差在-4.9~3.8 m 内波动,速度误差在±0.47 m/s 内波动。可见本文对系统设计的自适应调节策略,在故障发生后经历一个短暂的调节时间,误差越来越小直至趋近于0,使系统达到预期的性能,实现速度位移的渐近跟踪。
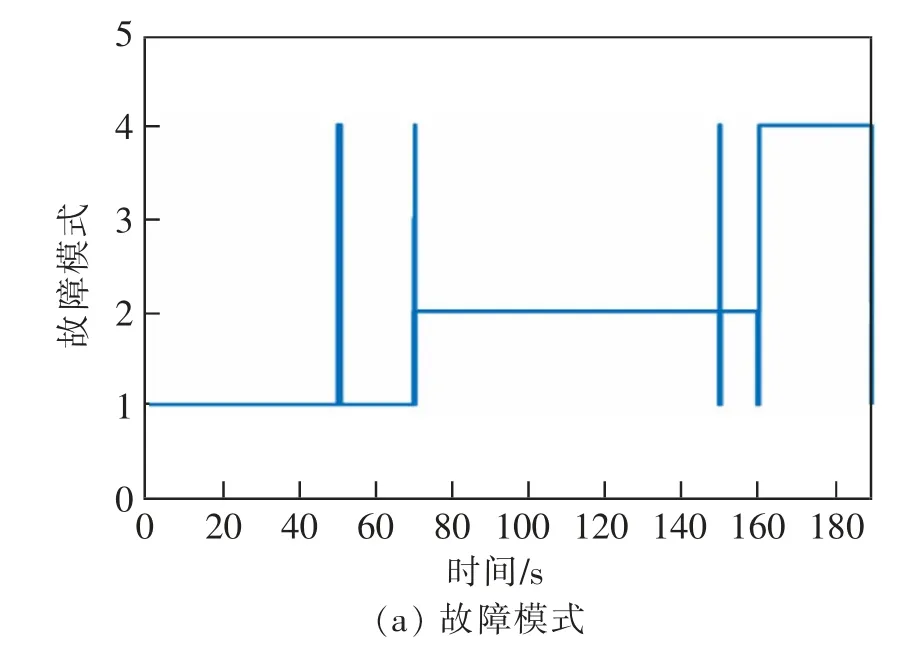

图2 高速列车自适应故障调节跟踪误差曲线Fig.2 Adaptive fault adjustment tracking error curve of high-speed train
本节选用基于滑模技术的方法与本文方法的效果进行对比,见图3 和图4。 从图3(a)可以看出,通过区间滑模观测器的方法,尽管能诊断出故障模式,但诊断时间需要20 s 左右,且切换频繁,容易造成误诊。 图3(b)和图3(c)分别反映了发生常值故障和组合故障时,实际故障大小与诊断出的故障大小之间的误差,常值故障诊断误差经过30 s 左右的时间稳定在50 A, 组合故障的诊断误差也未趋近于零。 相比于本文的设计方法,基于滑模技术的诊断误差较大,本文的诊断方案更简单准确。
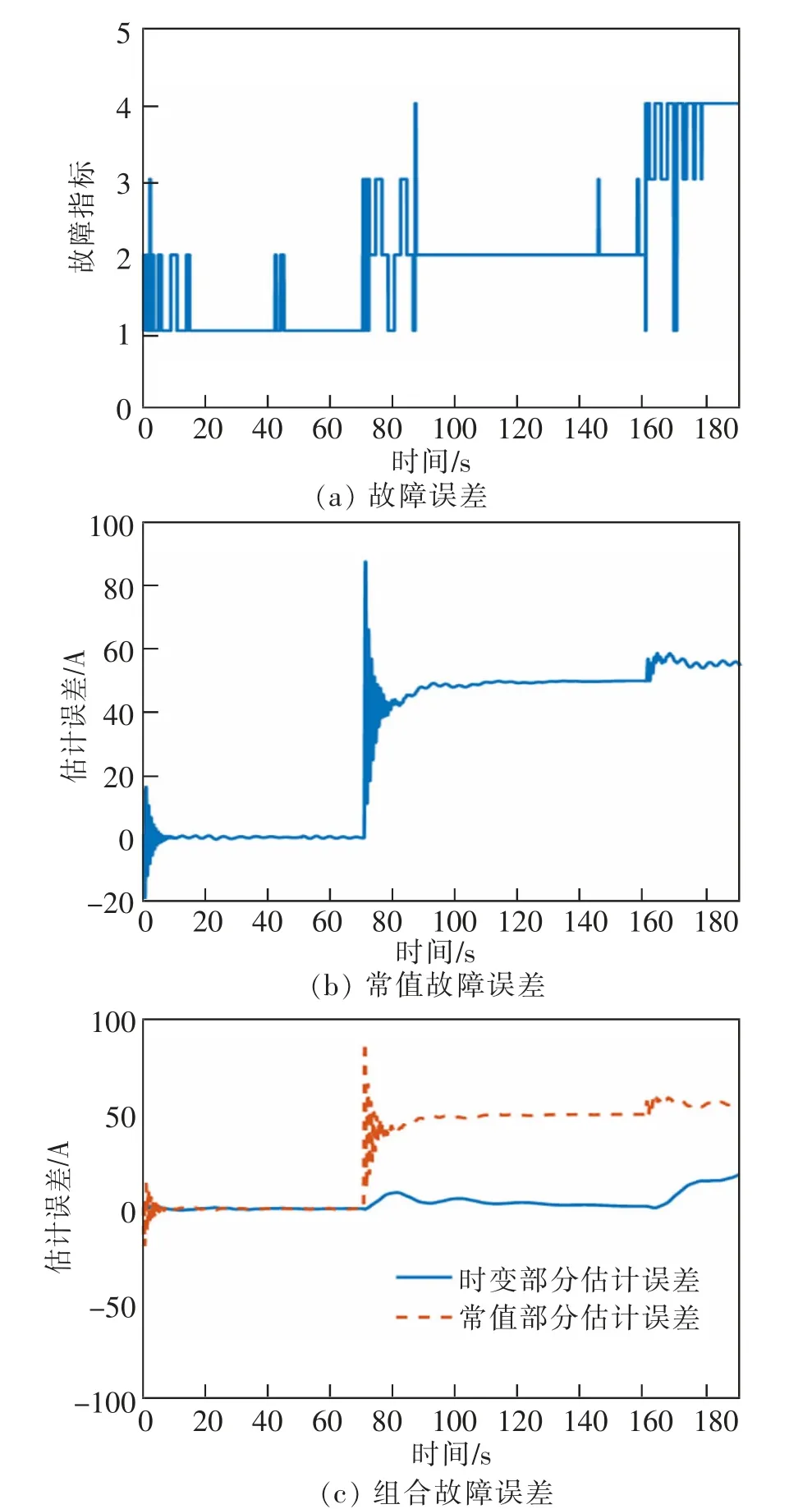
图3 基于区间滑模观测器的故障诊断Fig.3 Fault diagnosis based on interval sliding mode observer
通过图4 可以看出,在使用滑模控制器对发生故障的高速列车进行调节后, 位移误差在-90.6~87.3 m 之间波动,速度误差在-3.5~5.4 m/s 内波动,尽管可以实现故障调节, 并实现对给定曲线的跟踪,但误差相较于本文设计方法的误差更大。 综合分析,本文的诊断效果与调节效果更佳。

图4 基于滑模控制的故障调节误差Fig.4 Fault adjustment error based on sliding mode control
4 结论
在高速列车动力学模型的基础上, 考虑牵引电机产生的影响,深入到牵引特性层面进行建模。
1) 采用基于多模型的方法设计高速列车牵引电机故障自适应诊断与调节策略, 该方法运用多模型的思想设计了多个估计器, 极大地简化了故障诊断策略; 运用自适应方法善于处理系统不确定性的优势设计了故障调节控制器, 实现了对给定速度曲线的渐近跟踪。
2) 进一步分析高速列车牵引电机故障, 建立更加精确的牵引电机故障模型和更加完备的故障模式集是下一步的研究方向。
