面向密集热点区域的多层异构网络建模方案

吕亚平，贾向东，2，陈玉宛，路 艺

（1.西北师范大学计算机科学与工程学院，兰州730070；2.南京邮电大学江苏省无线通信重点实验室，南京210003）

0 概述

随着高速多媒体应用和高密度物联网设备的普及，未来5G/B5G 网络将会是基站（Base Station，BS）密集部署的热点通信网络，现有的蜂窝网络也将向小区密集化和以用户为中心的小型基站（Small Base Station，SBS）部署方向发展。

由于实际部署在多层5G HetNets 中的BS 位置表现出不规则性，因此随机几何空间模型被视为HetNets 精确建模和分析的重要工具［1-2］。在该方法中，大规模无线网络被抽象为点过程［3-4］，从文献［5-6］的研究中可以得出将BS 的分布视为一个点过程的原因。通过蒙特卡洛模拟，文献［7］研究得出理想六边形蜂窝系统下行链路信号干扰比的分布，接近根据齐次泊松点过程（Poisson Point Processe，PPP）部署BS 的蜂窝系统。在上述文献的启发下，文献［8-10］采用基于随机几何的模型对蜂窝网络性能进行评估，且已有大多数工作都将蜂窝网络建模为传统的理想六边形网格模型。然而，上述研究只将BS 和用户设备（User Equipments，UE）在每层中的位置建模为独立的PPP。在基于热点的5G HetNets中，当UE 和BS 之间存在相关性时，UE 和BS 之间的独立性假设可能不太准确。在实践中，虽然传统宏基站（Macro Base Station，MBS）的部署较一致，但为了满足全覆盖要求，又部署了其他类型的SBS，如微微基站（Pico Base Station，PBS）和毫微微基站（Femto Base Station，FBS）。因此，SBS 有望部署在拥挤或热点地区，以修补覆盖死区，这实际上耦合了UE 和SBS 的位置，使UE 和SBS 之间存在一定的相关性［11］。

虽然现有研究大多利用UE 和SBS（如PBS）之间的耦合，但在现实中，由于热点区域中密集UE 在短时间内引起数据速率突然激增，可能导致以集群为中心的BS 过载。在此情况下，需要在以集群为中心的部署模式下部署更多的低功耗FBS 作为UE，为过载BS 提供流量分流。在实践中，对于高密度HetNets，一个通用的模型是从热点区域中抽象出集群中心并建模为PPP。UE 和所有SBS 均分散在热点中心周围，并建模为泊松簇过程（Poisson Cluster Process，PCP）。虽然这种部署利用UE 与中心之间的耦合以及所有SBS 与中心之间的耦合，但对活动节点的位置呈空间分离的场景单纯使用PPP 和PCP来建模是不现实的，更合适的模型是泊松洞过程（Poisson Hole Process，PHP）。此外，文献［2-10］仅研究了单层蜂窝网络或者两层异构网络，并未对三层异构网络进行建模和研究。

本文在PPP 和PCP 的基础上结合PHP，提出一种面向密集热点区域的三层异构网络建模方案，以应用于移动UE 和FBS 都集中部署或分散在公共集群中心的网络场景。此外，本文还分析有序和非有序FBS 这2 种情况下不同网络参数对级联概率的影响。

1 网络建模

本文考虑一个三层异构蜂窝网络，如图1所示，其中，第1 层、第2 层和第3 层分别由MBS、PBS 和FBS 组成，分别称为M 层、P 层和F 层。所有MBS 都配有大规模多输入多输出（Multiple-Input Multiple-Output，MIMO）天线NM，所有PBS 都配备传统的MIMO 天线NP，所有FBS 和UE 都是单天线。利用简单的线性迫零波束形成（Zero Forcing Beamforming，ZFBF），每个MBS 和PBS 可以同时分别与SM个和SP个UE 进行通信。MBS 和PBS 的空间位置分别建模密度为λM和λP的独立PPPΦM和ΦP，假设整个网络在可用带宽W低于6 GHz 的频带上工作。

与MBS 和PBS 的空间分布不同，本文在PHP 的辅助下对FBS 和UE 的空间分布进行建模，PHP 是拥挤或热点区域移动UE 更真实的空间分布模型。同时，为了进一步提高容量，本文在PBS 周围密集部署FBS，从而实现PBS 位置与UE 和FBS 的耦合。此外，除建模UE 簇分布，本文还假设剩余的UE 服从PHP。

本文将FBS 的位置建模为密度λF的托马斯簇过程（Thomas Cluster Process，TCP）ΘF，其父点过程服从ΦP［12-13］，即这个点过程ΘF是由散布在父点过程ΦP周围的簇成员（FBSs）按照方差为的对称正态分布形成的，每个簇中的平均点数为。为了提高小区边缘UE 的性能，采用PHP 对簇边缘的点进行建模。

在给定父点过程ΦP中PBS 的覆盖半径为R2，在PBS 覆盖区域内的点ΘF被建模为 PCP，称为簇中心FBS；余下的FBS 点被建模为，称为簇边缘FBS。UE 的位置遵循空间密度为λU的任意独立点过程ΘU。为了捕获耦合特性，UE 根据点的平均数为的TCP 独立地散布在父点过程ΦP周围。在PBS 覆盖区域内的点ΘU被建模为PCP，称为簇中心UE；剩余的点UE 被建模为，称为簇边缘UE。

2 UE 分类和距离分布

2.1 UE 分类

由上文可得，目标UE 可以与MBS、PBS 或FBS相级联，此外，对于给定的级联，目标UE 分为簇内UE 或簇外UE，所有这些情况使UE 类型变得更复杂。图2所示为UE 分类情况，具体如下：

图2 UE 分类情况Fig.2 Classification of UE

1）簇中心UE 和簇边缘UE 过程：簇中心UE 过程ΦCUE是在PBS 覆盖范围内UE 点的集合，簇边缘UE 过程ΦEUE是剩余UE 点的集合。

2）簇中心FBS 和簇边缘FBS 过程：簇中心FBS过程ΦCFB是位于PBS 覆盖范围内的FBS 集合，簇边缘FBSs 过程ΦEFB是剩余FBS 集合。

3）簇中心宏小区UE（MUE）、微微小区UE（PUE）和毫微微小区UE（FUE）过程：簇中心MUE、PUE 和FUE 过程ΦCMU、ΦCPU和ΦCFU分别表示与MBS、PBS 和FBS 级联簇的中心UE 的集合。

4）簇边缘MUE 和FUE 过程：簇边缘MUE 和FUE 过程ΦEMU和ΦEFU分别表示与MBS 和FBS 级联的簇边缘UE 的集合。

基于簇UE 的分类，本文根据带宽分配因子η将可用的总带宽W分成两个正交的子带宽W1和W2，因此，W1=ηW，W2=(1-η)W。假设W1被分配给为簇中心UE 提供服务的PBS，W2被分配给为簇边缘UE提供服务的MBS，则簇中心FBS 与MBS 共享子带宽W2，簇边缘FBS 与PBS 共享子带宽W1。

2.2 距离分布

忽略簇和洞的重叠影响，在随机选取的簇中随机选取一个目标UE，本文将其称为代表簇。根据Slivnyak-Moche 定理，在Borel 空间上的点过程是PPP，当且仅当Palm 分布几乎处处与原分布定理一致。因此，对以xP0∈ΦP为中心的代表簇中位于原点的目标UE 进行分析是合理的。

服务于目标UE 的BS 被称为标记BS。由于MBSs 的位置被建模为密度λM的齐次表示目标UE 到最近MBS 的距离，距离的PDF由给出，其中，xM∈ΦM。将目标UE 到簇中心PBS 的距离记为‖x‖

P。

对于FBSs，本文分别在有序和非有序情况下考虑目标UE 到代表簇中FBSs 的距离‖x‖F的集合。在有序FBSs 的情况下，考虑在同一簇或代表性簇中最接近目标UE 的FBS，其相应的距离记为，该方法产生了较少的路径损耗。然而，在非有序FBSs 的情况下，在代表簇中随机选择FBS，其相应的距离表示为，该方案为ΘF中每个UE 接入FBSs 提供了公平的机会，其优点是网络不需要额外的瞬时信道状态信息，但在某些网络中由于基础设备性能较差而无法获得这些信息。

其中，I0(·)表示零阶、距离的方差修正的第一类贝塞尔函数。然而，文献［15-16］研究结果表明，修正部分非常微弱，可以忽略。由于从代表簇中心到目标FBS 和UE 的距离分别是具有方差和的独立且非均匀分布的高斯随机变量，因此得到的目标UE 到FBS 的总距离也具有方差为的高斯分布，所以，可以使用方差的瑞利衰落来近似分布，即的PDF 近似为：

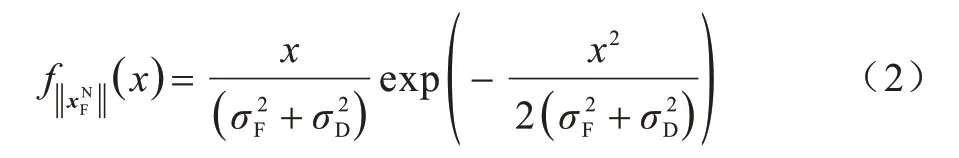
根据次序统计［17］和类似于式（2）的考虑，在有序FBSs 的情况下，目标UE 到最近FBS 的距离的CDF 为：

3 UEs 级联和访问距离分布

3.1 簇中心UEs 级联

由于UEs 可能属于簇中心也可能属于簇边缘，因此本文将分别研究簇中心和簇边缘UEs 的级联。

考虑到UEs 可能有3 种类型的级联概率（Association Probability，AP），即MBS、PBS 和FBS，以下利用长期平均接收信号功率模型，则目标UE 到位于xz∈ΦZ（xz∈ΘZ）处的BS 接收的长期平均下行链路信号功率［18］表示为：

其中，z∈{F,M,P}，GM表示MBSs 的大规模MIMO 平均阵列传输增益。在ZFBF 传输下，阵列增益由Gz=Nz-Sz+1 给出。尽管在z=F 时，Sz=1、Gz=1，但仍然使用式（6）的一般形式，该假设仍适用于后续分析，除非另有说明。表示路径损耗模型，其中，α是值为2 ～6 的路径损耗指数，β是与频率相关的常数值，通常设置为(c/4πfc)，并且c=3×108m/s，fc为载波频率［18］。

在接收信号的平均功率模型式（6）中，首先关注簇内UEs（即簇中心UEs）的级联。由于本文仅考虑蜂窝下行链路传输，因此使用最强的平均偏置接收功率（Average Biased Received Power，ABRP）来决定UEs 的级联［19］。ABRP 的基本思想是目标UE 根据ABRP 与强BS 相级联，因此，决定服务于目标簇中心UE 的BS 表示为：

其中，Bz表示z 层相同的偏移因子。因此，使用级联准则式（7），获得AP，具体变量定义如下：

当z=F 时，有Sz=1 和Gz=1。同时，由于簇中FBS的数量是固定的，因此，假设在有序和非有序FBSs 两种不同场景下从同一簇中选择服务的FBS。在有序FBSs的情况下允许目标UE 访问代表簇中最近的FBS；在非有序FBSs 的情况下允许目标UE 在代表簇中随机选择FBS。在此基础上，本文实现命题1。

命题1在有序FBSs 的情况下，目标簇中心UE与z层中一个BS 级联的概率分别为：

证明在有序FBSs 的情况下，首先计算目标簇中心UE 与位于毫微微小区层xF∈ΦF的FBS 的AP，即。在此情况下，计算如下：

在区域A 内通过应用密度为λ的PPP 的空概率，即exp(-λA)，则来自ΦM的干扰的级联概率表示为：

注意代表簇中只有一个PBS，并且目标簇中心UEs 落在PBS 半径为R2的覆盖范围内，目标UEs 到其簇中心的距离的CDF 可写为：

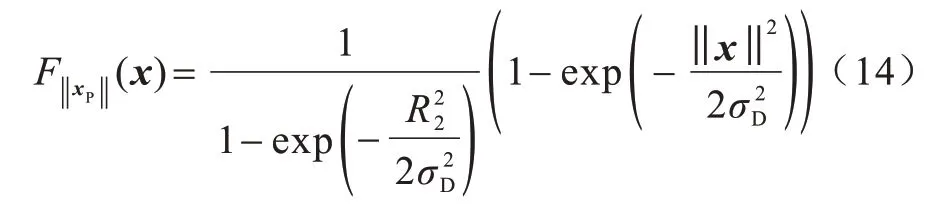
其中，σD是TCP 的高斯UE 分布的标准推导，由式（14）得出式（15）。因此，可进一步写为式（16），其中是目标UE 到代表簇中最近FBS的距离，其PDF 由式（2）给出。因此，结合式（2）和式（16）可得到目标簇中心UE 与FBS 的AP，即如式（17）所示。

当目标簇中心UE 与式（12）的具有对称性的MBS 相级联时，级联概率表示为：

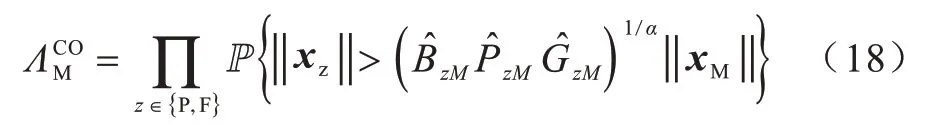
当z=P 时，结合式（14）中分布和PBS 的覆盖半径R2，可以得到式（19）。当z=F，利用式（4）中有序 FBSs的，则概率如式（20）所示。将式（19）和式（20）代入式（18），则可以进一步计算得到式（21）。对于密度为λM的PPPΦM，距离的PDF 为。因此，如式（22）所示。类似地，利用式（37）中距离的分布，目标簇中心UE 与唯一的PBS 的级联概率如式（23）所示。

利用与命题1 相似的论据，可以得到在非有序FBSs 情况下的AP，即推论1，其中推论1 可以用与命题1 相似的准则来证明。

推论1在非有序FBSs 的情况下，目标簇中心UEs 与z层中的一个BS 级联的概率分别如式（24）～式（26）所示。

由命题1 易得目标UE 到z 层服务BS 级联距离的PDF。在有序FBSs 的情况下，假设服务FBS、MBS 和PBS 分别位于和处，则目标UE到其服务FBS、MBS 和PBS 的级联距离分别表示为和且。根据这些假设，可以实现命题2。

命题2在有序FBSs 的情况下，假设目标簇中心UE 与z层中的一个BS 相级联，则级联距离和的PDF 分别如式（27）～式（29）所示。

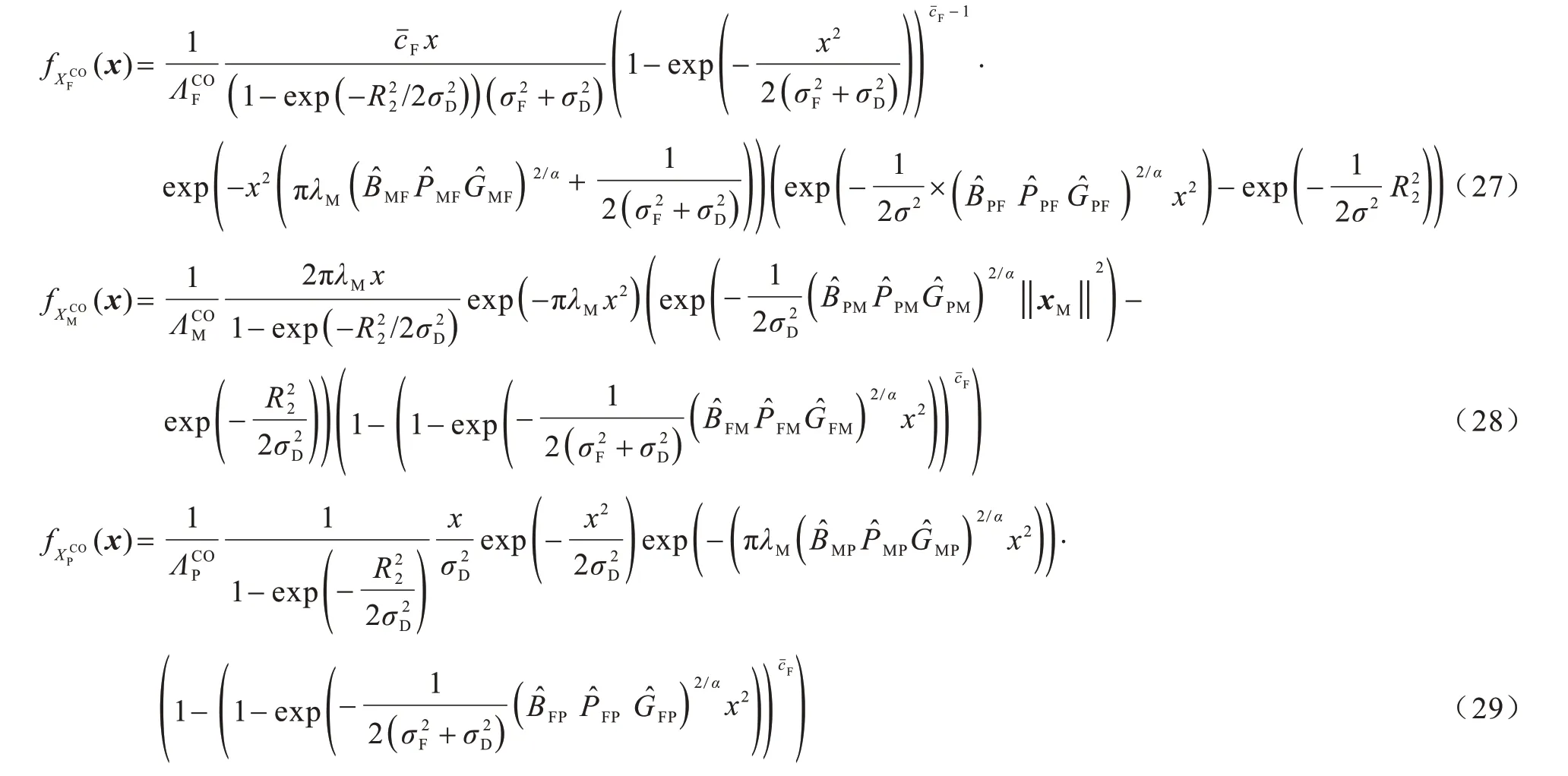
此外，在非有序FBSs 的情况下，推论2 给出了相应级联距离的PDF。

推论2在非有序FBSs的情况下，假设目标簇中心UE 与z层中的一个BS 相级联，则级联距离，且和的PDF分别如式（30）～式（32）所示。

3.2 簇边缘UEs 级联

在目标UE 位于PBSs 的覆盖范围之外时，簇边缘UEs 仅具有两种可能的级联类型，即MBS 和FBS，如图1所示。级联准则式（7）可以重新记为：

因此，对于有序FBSs 的情况，可以得到命题3。

命题3在有序FBSs 的情况下，目标簇边缘UE与z层中BS 的级联概率分别为：

推论3在非有序FBSs 的情况下，目标簇边缘UE 与z中一个BS 的级联概率分别为：

此外，在有序FBSs 的情况下，目标簇边缘UE 与其服务FBS 和MBS 的级联距离分别为和，且，由此可得命题4。

命题4在有序FBSs 的情况下，假设目标簇边缘UE 与z层中的一个BS 相级联，则级联距离和的PDF 分别为：

此外，在非有序FBSs 的情况下，目标簇边缘UE与其服务FBS 和MBS 的级联距离分别为和，且，由此可得推论4。

推论4在非有序FBSs 的情况下，假设目标簇边缘UE 与z层中的一个BS 相级联，则级联距离和的PDF 分别为：

4 仿真和数值分析

本章节进行模拟实验和数值结果分析，以验证HetNets 建模方案的正确性，并说明不同网络参数对级联概率的影响。在整个网络中，假设所有链路的路径损耗指数均为α=2，MBSs 和PBSs 的位置分别被建模为密度λM=(1～10)MBSs/(π×km2)和λP=10λM的独立PPPs，PCP 中的点ΘF和ΘU以方差10～1000 和分布在父点周围。活动FBSs 和UEs 的平均数目分别为和总的可用带宽为W=20M Hz。参考文献［20］，本文参数取值如表1所示。

表1 系统参数及其取值Table 1 System parameters and their values

图3 目标簇中心UE 与FBS、MBS 和PBS 的级联概率Fig.3 Association probability of target cluster-center UE with FBS，MBS and PBS

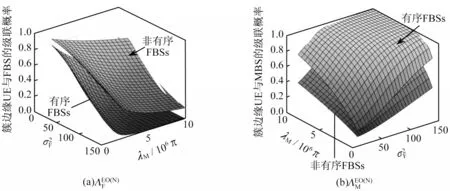
图4 目标簇边缘UE 与FBS 和MBS 的级联概率Fig.4 Association probability of target cluster-edge UE with FBS and MBS

由于只有MUEs 和FUEs 不在PBS 的覆盖范围之内，因此图4 给出了和。由于UEs 与MBS 级联的概率更多，因此簇边缘UE 与MBS 的随密度λM增加而增加。方差的增加表明更多的FBS 将远离目标簇边缘UE，根据全概率定律，可以得出随方差和密度λM的增加而减小。与图3（a）中的类似，图4（b）表明在有序FBSs下的AP 小于非有序FBSs 下的AP，这是因为在非有序FBSs 下，目标UE 随机选择其服务的FBS，使得目标UE 与FBS 获得了更多的级联概率。

5 结束语

本文针对密集热点通信场景，提出一种三层HetNets建模方案。分析不同网络参数对UEs级联概率的影响，并在有序FBSs 和非有序FBSs 两种情况下，分别对比目标UE 与FBS、MBS 和PBS 级联的AP 大小。下一步将在本文方案的基础上对网络覆盖概率进行研究，并且将在该网络模型中加入D2D 用户，研究D2D 通信模式下的网络覆盖概率。