基于深度学习提高数学教学效果的对策分析

颜秀容

摘 要：小学数学深度学习模式的构建，是培养学生数学思维能力，发展学生数学核心素养的有效途径。新课程改革背景下，小学数学教师要积极构建深度学习课堂，培养学生高阶思维，提高数学教学有效性。

关键词：小学数学;深度学习;有效性

所谓深度学习，是指学习者在理解学习的基础之上，能够批判性地学习新的思想和事实，并能够将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，做出决策和解决问题的学习。深度学习是相对于浅层学习而言的一种学习模式。在教育改革不断深入发展的背景下，教师在实施教学的过程中，应当结合教学需要，积极构建深度学习的课堂，深化学生对知识的认知，提高学生的学习思维能力。基于深度学习的视角，数学作为一门思维性极强的学科，在数学教学中构建深度学习的模式及其重要。文章中，笔者立足深度学习视角，探索在小学数学教学中构建深度学习模式的意义、现状极其对策。

一、 小学数学教学中构建深度学习课堂的意义

（一）全面提高学生的数学思维品质

数学是思维的体操，思维是数学的心脏。在数学学习中，学生数学思维能力的高低，直接决定其数学学习效果的好坏。在数学教学的过程中，强化对学生思维品质的训练极其关键。美国教育家布鲁姆的教育理论认为：在知识习得的过程中，学生的思维有低阶思维和高阶思维之分。高阶思维对应的学习方式是深度学习，低阶思维对应的学习方式是浅层学习。低阶思维的学习，体现为“记忆—理解—应用”，这是一种依靠模仿和记忆来获取知识的学习模式，相对而言比较机械;而高阶思维的学习方式，则是“分析—创造—评价”，强调学生在理解的基础上记忆知识，发挥其批判性思维和创造性思维。立足高阶思维与低阶思维的区别、深度学习与浅层学习的区别我们可以轻松地总结出：在小学数学的教学中，教师积极构建深度学习的数学教学课堂，培养学生的高阶思维，提高学生在数学学习中的分析、总结和归纳能力，促使学生数学思维能力的提升。由此可见，和浅层学习模式相比，深度学习教学模式的构建，是全面提高学生数学思维品质的需要。

（二）发展学生数学核心素养

在核心素养视角下，数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析共同构成了学生数学素养的六个维度。在核心素养视角下，教师在数学教学中，应当改变过去应试化的教育模式，培养学生适应于未来发展和社会发展的必备品格和关键能力，强化学生知识、技能、态度和价值观等的综合表现。而传统的以考核为目标的数学教育模式，导致学生在知识习得的过程中，常常是在机械记忆的基础之上理解知识，这是一种典型的浅层学习模式，不利于学生数学思辨能力、独立思考能力以及知识迁移能力的提升。在深度学习视角下，小学数学教师在教学的过程中，强化学生在数学学习中自主学习能力、思辨能力、分析和创造能力的培养，这种立足知识与技能，强化学生对知识理解而后记忆的教育模式，能够有效地革新传统的数学教育模式，进而达到发展数学核心素养的目的。

二、 基于深度学习，提高数学教学效果的对策

（一）整体分析内容，设计长程学习目标

1. 设定长程目标

小学数学教科书的内容通常以单元为单位，并且单元的内容顺序排列以反映数学学习的内容。该单元的主要内容，包含最重要的要点，学生掌握知识点，学生了解重要的数学内容和基本单元概念，把握知识迁移和解决问题的水平，并设定学生单元目标及长期目标。这些目标称为单元根对象。在该目标的指引下，再结合课程设计，使得缩短的目标是长期目标的序列点，但它们始终会与长期目标保持一致。例如，三年级“分数的初步认识”，主要目标旨在理解和运用分数的含义，了解如何比较分数大小并进行计算。

2. 整体分析核心内容，设计靶向长程目标

小学数学教材内容的编排通常是递进编排式，但是，对小学数学内容进行梳理时会发现，一些具有相同的数学思想包含在核心内容中，核心内容由具有共同特征的基本技能，数学知识组成，所有这些数学思想都像目标中心。随着学生年龄的增长，学习内容变得越来越多，并且逐渐扩散到中心外水平。这些内容不管怎么扩展和发展，最主要的是围绕核心思想来扩展。例如，学生探索计算平面图面积的最重要的内容是计算方法，数学的核心概念转换，专注于数学的推理能力。我们紧随这个中心，然后慢慢扩展：平行四边形的面积→三角形的面积→梯形的面积→圆形的面积→圆柱体的体积→……因此，我们必须学会学习和理解数学思想以及各种数学内容的核心知识，使之所有内容都围绕着这个目标落实。

（二）深化知识理解，引导深度学习

常言道：“基础不牢，地动山摇。”在数学教学中，深化学生对知识的理解，是提高教學质量的关键，同时也是促使教学改革创新的有效途径。小学数学的教育，课本教材是学生获取知识的主要途径，同时也是教师进行授课的依据。小学数学教师在教学的过程中，要认真研读教材，深入剖析，把握知识的内涵，深化学生对知识的理解，引导深度学习。

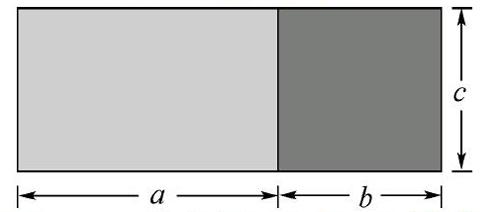
例如，在“乘法分配律”的教学中，笔者并没有让学生直接记忆乘法分配律的表示方式，而是融入数形结合思想，立足问题导学教学模式，引导学生推导乘法分配律的表示方式。图形如下：

通过图片展示，笔者提出问题：同学们，要求出图中图形的面积，有哪几种表示方式呢？学生积极主动思考，并得出了不同的答案，有学生用a×c+b×c表示，也有学生用（a+b）×c表示。笔者继续提问：哪一种方式的计算是正确的呢？学生深入思考，发现两种表示方式都是正确的计算方式。笔者：既然同学们发现两种计算方式都是正确的，说明：（a+b）×c=a×c+b×c，而这个公式所表达的，就是乘法分配律。这种自然的知识过渡，能够让学生对知识的理解更加深刻，有效地改变过去让学生死记硬背相关知识的学习方式，实现深度学习的教学目标。

（三）科学问题导学，引导深度学习