全钢子午线轮胎的滚动阻力效应分析
2021-07-24王晓东孙佳佳孙宝余
王晓东,孙佳佳,孙宝余
(三角轮胎股份有限公司,山东 威海 264202)
滚动阻力系数是轮胎性能表征的一个关键参数。随着欧盟标签法的深入推进,终端客户及主机厂对轮胎滚动阻力的要求愈加严格,对滚动阻力效应的研究也随着产品的更新换代而不断取得突破[1-3]。
为系统研究各效应项对轮胎滚动阻力的影响,本工作对滚动阻力测试结果的相关参数进行统计分析,验证轮胎的规格、花纹、应力(F)、测试充气压力、胎面胶损耗因子(tanδ)和行驶速度(v)对滚动阻力系数的影响,以为轮胎产品开发及优化提供预测依据和方向。
1 实验
1.1 测试设备
本次测试采用的是三角轮胎股份有限公司国家工程实验室的TSⅡ001型滚动阻力测试机床。
同一条轮胎测试的滚动阻力系数标准偏差(σRRC)为0.09,规格内稳健σRRC为0.12,规格内σRRC为0.18,设备检测范围为5.5~8.5;检测的概然误差σpe(分布中相对于概率分布中点两侧对称区间内分布概率等于50%的点与中点的距离,即概率分布从25%~75%区间所对应的随机变量区间长度的一半;对于正态分布,σpe与σRRC具有固定的转换关系)主要判断在检测范围内误差主要来自于设备还是来自于测量件。本试验σpe=0.675σRRc≈0.06,检测σRRC与设备检测范围比例最大值为0.06/(8.5-5.5)×100%=2%。
说明该设备满足测量条件的要求,同时可确保测量的变差主要来自于产品而非设备。
1.2 测试方法
滚动阻力测试方法采用汽车轮胎滚动阻力检测标准[4],在不同速度和充气压力下对轮胎进行滚动阻力检测。
2 结果与讨论
对5个规格的82个产品进行滚动阻力系数检测,并分别构建数学模型进行效应检验,对其影响因素进行拟合分析。
2.1 数学回归模型构建
对滚动阻力系数(RRC)和轮胎的规格(ai)、花纹(bj)、v、F和tanδ进行了回归分析,所得数学模型如下。
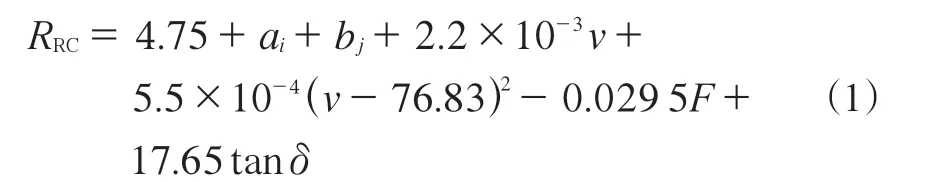
式 中,i与j分 别 取1—5,a1,a2,a3,a4和a5对 应 的轮胎规格分别为205/75R17.5,215/75R17.5,225/70R19.5,235/75R17.5 和245/70R19.5,a1—a5分 别 取0.049,0.062,0.349,-0.102 和-0.355;b1—b5分别对应5个不同花纹,取值为-0.287,-0.086,0.257,0.332和-0.215。
2.1.1 显著性分析
各影响因子对滚动阻力系数影响的显著性结果如表1所示。
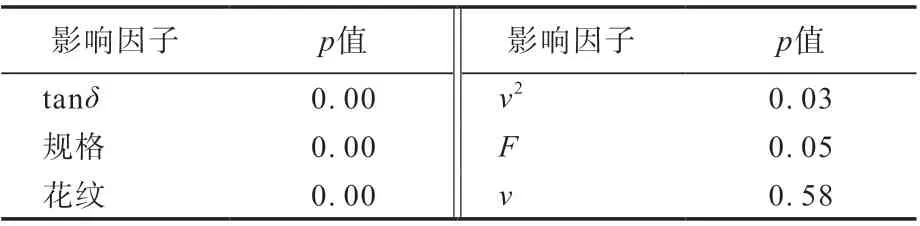
表1 滚动阻力系数影响因子显著性对比
从表1可以看出:对轮胎滚动阻力系数影响最大的3个因子分别为tanδ、轮胎规格和花纹;其次是v的二次项和F,且其显著性水平较高;由于对v采用了二次项回归,也就意味着不能简单删除进入回归模型但概率并不大的v一次项。
2.1.2 方差分析
该模型的方差分析结果如表2所示。
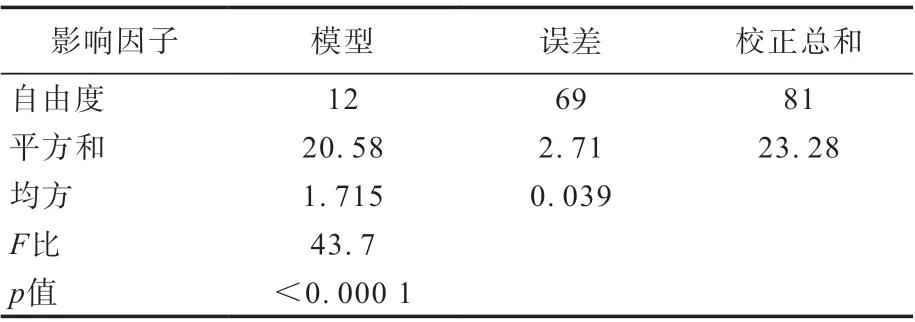
表2 滚动阻力系数回归模型的方差分析
从表2可以看出:该模型的无效p值远小于统计值阈(0.05),因此该模型可以有效地反应滚动阻力系数的变异。
2.1.3 失拟分析
失拟检验是一种判断回归模型是否可以接受的假设检验,H0为模型不存在失拟,主要通过残差方差进行分析。残差方差由随机误差和失拟误差两部分组成。失拟检验是失拟误差方差与随机误差方差的比值作为F值来进行F检验;若p值<α,则模型无法与数据充分拟合,需要添加项(通常是二次项或更高次项)或对数据进行转换;若p值>α,则不能断定模型与数据无法进行很好的拟合,接受H0假设。
为防止出现滚动阻力效应因子的二次甚至更高次的效应项,应对模型进行失拟分析。该模型的失拟结果如表3所示。
从表3可以看出,失拟p值>0.05,则该模型可认为不存在失拟。
2.1.4 回归分析汇总
该模型的预测值与实际值的线性关系如图1所示。
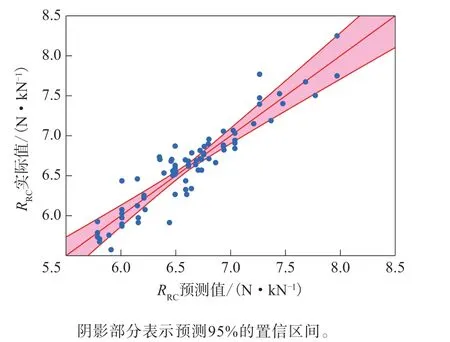
图1 滚动阻力系数预测值与实测值的关系
从图1可以看出,通过构建模型得到的滚动阻力系数的预测值与实际值基本呈线性关系,不存在弯曲或者倾斜。经计算,该模型的相关因数(R2)和调整R2分别为0.884和0.864,说明该模型的变异比例明显高于随机误差,能有效反映滚动阻力系数的变化。
2.1.5 残差分析
回归模型的残差具有不可预测性和随机性,进行残差分析以验证回归模型的有效性。其中不可预测性使用残差图检查;随机性采用正态性分析以验证残差的随机性。
2.1.5.1 不可预测性分析
对构建回归模型后的滚动阻力系数残差与预测值作残差图,如图2所示。
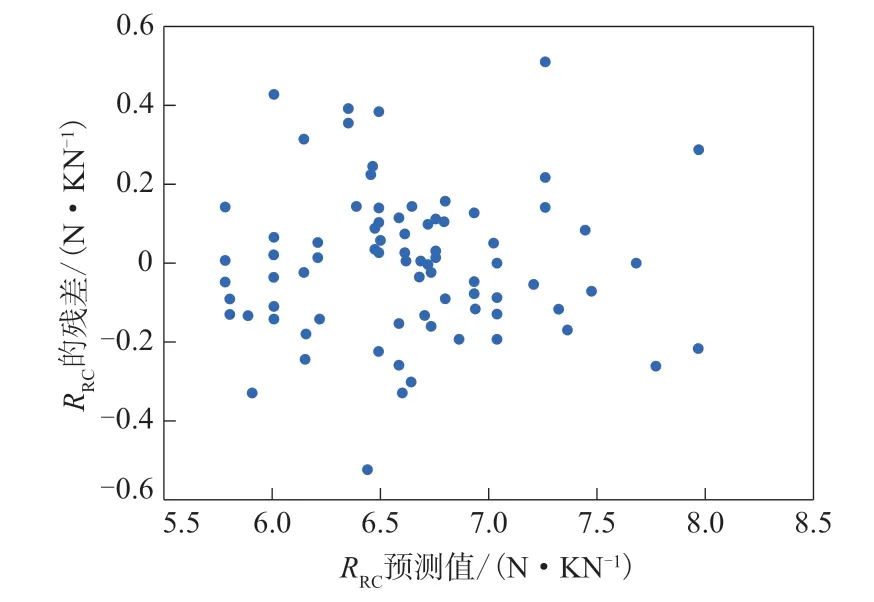
图2 滚动阻力系数回归模型的残差图
从图2可以看出,滚动阻力系数的残差与预测值之间不包含单一趋势或者弯曲信息。
2.1.5.2 随机性检验
回归模型的正态性检验是残差分析的数学公式之一,为保证残差的随机性,一般会对残差进行正态检验。经检验,该模型拟合的滚动阻力系数预测值与实际值的残差基本符合正态分布。
采用Shapiro-Wilk方法进行正态分布优度检验,可得W值为0.983 469,p值为0.373 8。残差的正态检验显示滚动阻力系数实测值与模型预测值的残差符合正态分布,可认为拟合模型有效。
因残差不存在可预测性,同时符合正态分布,因此可以认为该回归模型很好地体现各效应项因子对滚动阻力系数的影响。
2.2 拟合v二次项的探索
滚动阻力系数回归模型中除了常用的一次项拟合外,还增加了v的二次项拟合,从而控制模型的失拟风险。
轮胎的滚动阻力系数与v不呈现线性关系,当v低于80 km·h-1时滚动阻力系数与其呈负相关,当v高于80 km·h-1时滚动阻力系数与其呈正相关。为保证分析的严谨性,应先对v进行线性分析,线性模型合理且存在失拟则证明确实存在v的高阶效应项,反之应摒弃其高阶效应项。
2.2.1 均值和线性关系的显著性研究
为验证一次效应是否能够表征滚动阻力系数的变化,建立了滚动阻力系数和各效应项的线性回归模型,模型的效应分析和失拟分析分别如表4和5所示。
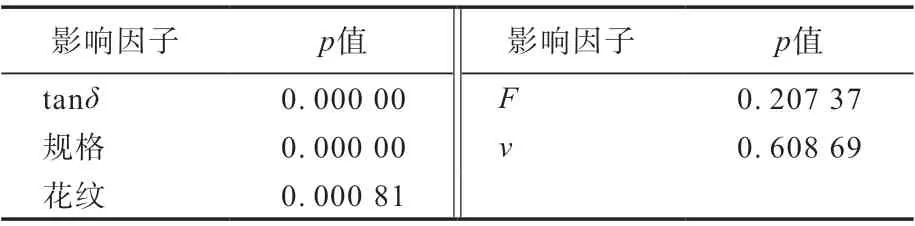
表4 均值和一次项拟合效应分析
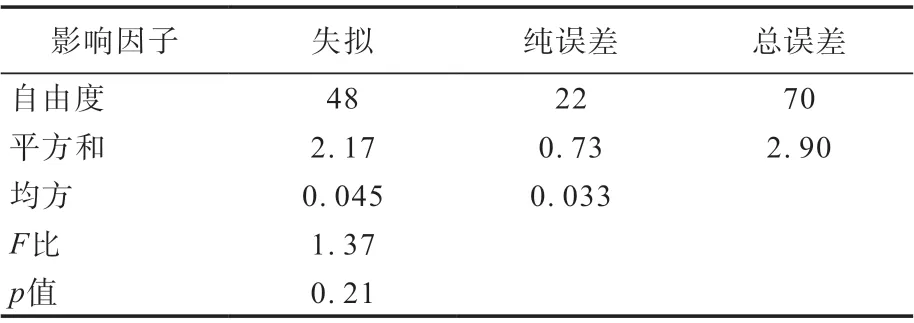
表5 均值线性模型的失拟分析
从表4和5可以看出:线性拟合模型中失拟不显著;v和F的滚动阻力系数效应不显著,需要排除v后重新进行回归分析。
2.2.2 排除效应不显著项目的回归分析
排除v和F后对回归模型进行效应分析,可得tanδ、轮胎规格和花纹的p值均为0,说明各影响因子对滚动阻力系数的影响显著。同时对排除v和F后的回归模型进行失拟分析,结果如表6所示。
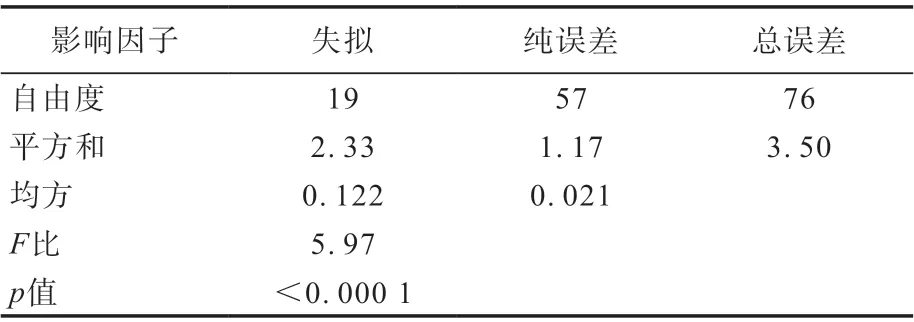
表6 去除效应不显著的因素后模型的失拟分析
从表6可以看出,排除v和F后的回归模型出现了明显的失拟。结合表4—6可以看出,回归模型应存在高次项。
2.2.3 滚动阻力系数测试的速度依赖性分析
在不同检测速度条件下对同一产品的滚动阻力系数进行回归分析,结果如图3所示。
从图3可以看出,同一产品的滚动阻力系数在一定速度范围内可以很好地采用二次项进行拟合,即滚动阻力系数与速度在一定范围内可以认为是二次相关的[5]。
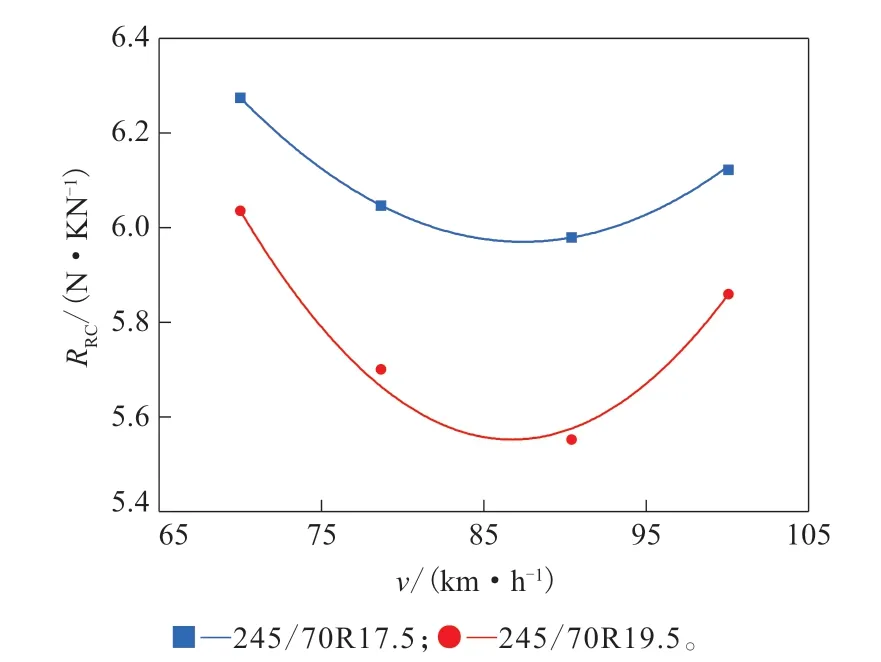
图3 滚动阻力系数与检测速度的相关性
2.2.4 滚动阻力系数与速度二次相关性的经验模型
依据ISO 28580—2018,在特定试验工况下,滚动阻力(FRR)的经验模型为:
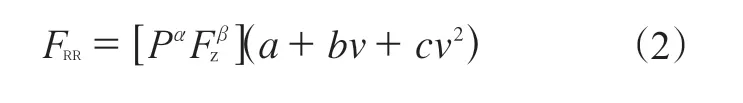
式中,P为充气压力,Fz为垂直负荷,α和β为幂次系数,a,b和c为滚动阻力系数与速度回归曲线系数。
结合统计分析的结论以及理论实践,在回归分析过程中考虑v二次项符合实际情况,也利于降低统计失拟的风险。
2.3 胎面配方对滚动阻力效应贡献率分析
通过该回归模型可以评估tanδ对轮胎滚动阻力的贡献率(即17.65tanδ/RRC)。各规格轮胎的tanδ对滚动阻力贡献率如表7所示。
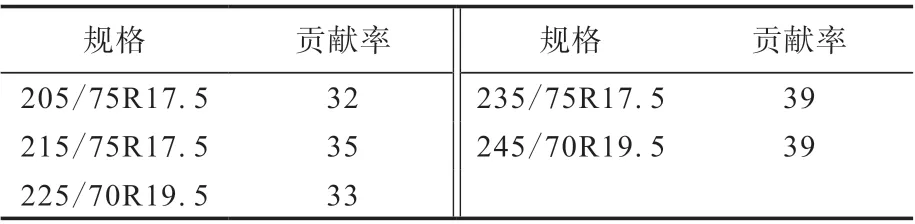
表7 各规格轮胎tan δ对滚动阻力贡献率 %
从表7可以看出:轮胎大部分滚动阻力效应来源于胎面胶的滞后损失,且随着轮胎规格的增大,tanδ对滚动阻力贡献率增大;随着轮胎角速度的降低,由密封气体压缩及流动的能量损耗以及轮胎其他部件所导致滚动阻力贡献率越来越小。理论上,充气轮胎滚动阻力的极限应为充气柔性轮胎的滚动阻力。
3 结论
采用回归模型分析轮胎规格和花纹对滚动阻力的影响,探索其他设计因素对滚动阻力的影响,而且构建回归模型的相对误差较小;回归模型的预测结果在后续的花纹扩展、产品抽样检测、品质控制和性能优化等方面具有很好的指导意义;同时将结构和配方设计的相关参数继续深入分解,最终体现在各种设计参数对轮胎滚动阻力的影响上;对探讨各种影响因素对滚动阻力的贡献率等方面提供了很好的借鉴。
