滑动轴承运行模态参数理论分析及试验验证*

王全召 陈 阳 张 浩 甄 冬 师占群

(河北工业大学机械工程学院 天津 300130)

滑动轴承由于其成本低、负载能力强等优点，在旋转机械中具有广泛的应用。然而，对滑动轴承故障的监测一直是一个难题。轴承在转子系统中属于薄弱的一环，对轴承的运行模态进行有效监测对整个转子系统的正常运行具有重要意义。能够反映轴承工作状况的参数主要有油温、油屑、振动信号、噪声信号、声发射信号等[1]。一般来说，油温在达到一定值之前对磨损故障不敏感；油屑检查需要的设备成本高且测试程序耗时长；声发射信号容易受到环境噪声的影响。相比之下，振动信号在实时监测[2]、抗干扰、对故障发生的敏感性等方面具有明显优势，并且使用非侵入性方法分析振动信号不会影响轴承的正常运行。但是，在振动信号分析时从激励源到传感器安装位置的传输路径复杂，因而从原始振动信号中提取有效故障特性比较困难。因此，在内部流体动力润滑[3]与外部振动信号之间建立准确的关系具有重要的意义。

运行模态分析方法主要有两类，即频域方法和时域方法。经典的时域方法使用随机子空间识别(SSI)，频域方法采用峰值拾取方法[4]和量子域分解(FDD)[5]。多数方法基于状态空间动态模型和傅里叶变换[6]的思想。

本文作者通过建立滑动轴承动力学模型，运用复模态分析方法，分别分析了转速、载荷和润滑剂黏度对模态参数的影响，并通过实验模态分析验证了理论分析的正确性。

1 理论分析

1.1 滑动轴承动力学模型

轴承的主要结构如图1(a)和(b)所示，即由轴颈、轴瓦和油膜组成。一般来说，轴承在工作时通常受不平衡离心力和径向载荷以及油膜中产生的流体动力的作用，它们会激发转子的工频及其谐波振动。同时，摩擦副表面与流体油膜之间的微观流固耦合作用所产生的小振幅、宽频带的随机激励，会激发转子轴承系统的随机共振。

滑动轴承的动力学模型如图1(c)所示，将轴瓦、壳体所组成的支撑系统离散为通过弹簧和阻尼连接的质量节点，建立如下滑动轴承运动微分方程[7]：

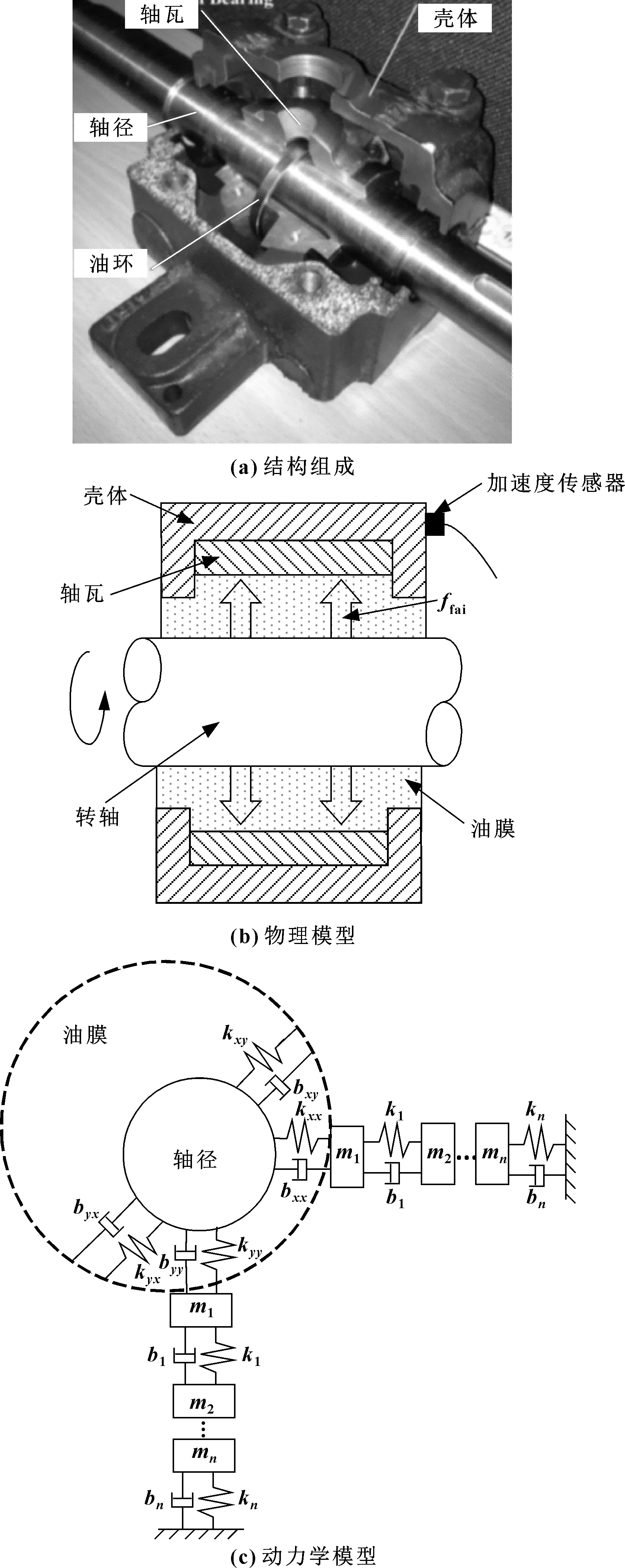
图1 自对中滑动轴承结构、物理模型和动力学模型

(1)

式中：[M]、[Beq]、[Keq]分别表示滑动轴承的质量、阻尼、刚度矩阵；{u}={u1,......,un}T表示位移矢量;{fext}、{fh}是外力和油膜力;{ffai}是由流体与表面相互作用(FAI)引起的随机力[8]。

与转轴相比，轴承的模态更加复杂，因此文中将重点研究轴承的振动信号。而轴承的振动信号与宽径比和Sommerfeld数、负载、速度和润滑剂黏度[9]有关。如果外力{fext}由油膜力{fh}平衡，那么方程(1)可以简化为

(2)

式中：[Beq]、[Keq]是考虑流体动力润滑的等效阻尼和刚度矩阵。

由于油膜的影响，轴承的模态参数不仅受结构的质量、刚度以及阻尼的影响，还与流体动力润滑状况有关。由于轴承间隙通常非常小，一般可以忽略油膜的流体模态，油膜的影响一般可以用动态特性系数来评估，即刚度系数(kxx，kxy，kyx，kyy)和阻尼系数(bxx，bxy，byx，byy)。因此，为了对滑动轴承进行模态分析，需要计算不同运行工况下的动态特性系数[10]。

动态系数可以转换为量纲一化形式如下：

(3)

式中：C是轴承的间隙；Ω是转速；W是径向载荷。

1.2 复模态分析

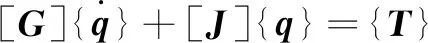
(4)

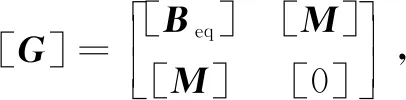
det(v[G]+[J])=0

(5)

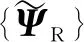
(6)

(7)

借助左、右特征矩阵，可以对矩阵[G]和[J]进行对角化。

(8)

(9)

对状态方程(4)进行傅里叶变换得：

(10)

由于特征向量的正交性,方程(10)可以写成下面形式:

(11)

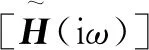
(12)

1.3 模态参数的提取

随机子空间算法[12-13]的基础是离散时间状态空间模型，假设输入为白噪声，利用白噪声的特性来计算。通过QR分解，奇异值分解和最小二乘法计算离散后的状态矩阵并获得模态参数。

1.3.1 状态空间模型的建立

系统的运动微分方程可以表示为

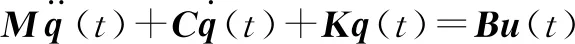
(13)

经过变换后，式(13)也可以写为

(14)

式中：x(t)为状态向量；Ac为状态矩阵；Bc为输入矩阵。

振动系统的响应信号可以用y(t)表示：

(15)

通过式(15)变换，可以写为

y(t)=Ccx(t)+Dcu(t)

(16)

由此得出系统的连续状态空间模型。

在实际情况下，测量出的都是一些离散的时间点，而且噪声的影响也相当大，需要将连续的时间模型离散化，输入是不可测量的随机激励，而且无法将其与噪声区分清楚。因此需要将输入项与噪声项合并，获得随机子空间方法的基本模型，即为离散随机状态空间模型。

xk+1=Axk+wk

(17)

yk=Cxk+vk

(18)

式中：A为系统状态矩阵；C为输出矩阵。

1.3.2 模态参数识别

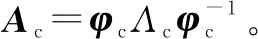
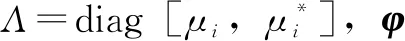
(19)

式中:λi为系统的特征值；Δt为采样时间间隔。

由固有频率ωi、特征值λi和模态阻尼比ξi的关系，可以得出结构的第i阶固有频率、阻尼比和模态振型[15]。

(20)

2 模态参数分析

文中就流体动力润滑对轴承模态参数的影响进行了数值仿真。假定模型为3个由弹簧和阻尼相连的质量节点组成，第1个节点通过油膜与轴连接，第3个节点与底座相连。质量和阻尼的值分别设置为m1=m2=m3=5 kg，b1=b2=b3=10 N·s/m。

2.1 刚度影响分析

首先比较了在有润滑和无润滑条件下轴承的频响函数(FRF)。如图2所示为刚度不同情况下，在第1个节点水平方向上进行激励，并从第3个节点同一方向获得响应时，系统在有无润滑条件下的频响函数。若无油膜的影响，动态模型在水平和竖直方向上是对称的。因此，系统有3组模态参数，每组模态具有相同的频率和阻尼比。每个 FRF 中可以观察到3个峰值。在相同的质量和阻尼下，刚度系数越大则固有频率越高。

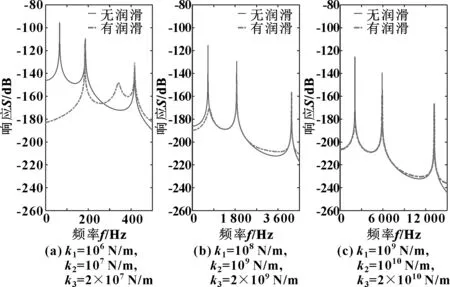
图2 刚度不同时系统的频响函数

滑动轴承的几何参数设置为：轴承宽度与直径相等，即L=D=0.1 m，油膜间隙C=10-4m。最初假定在轴表面上分布的不平度有3个波长，分别为0.1、0.067和0.033 m。相应的峰值分别为2×10-7、5×10-7和1×10-7m。在考虑润滑情况下，油膜不均匀导致不同方向的模态参数不同。其中一个方向的阻尼比通常较高，因此振动在很大程度上取决于阻尼比较低的一个方向。在其他条件相同的情况下，油膜刚度的不同会导致系统的固有频率不同。这里将系统刚度设置为k1=108N/m、k2=109N/m、k3=2×109N/m，然后计算不同条件下系统 FRF。结果如图2(a)所示，系统的前四阶模态受润滑影响。随着系统刚度的增加，只有前两阶模态受到影响，而分布在较高频段内的模态几乎与没有油膜的情况保持相同的固有频率，如图2(b)所示。进一步提高系统刚度，润滑对所有模态的影响更小,如图2(c)所示。此外，响应振幅和高阶模态的分布均不受润滑的影响，润滑的影响通常为一定频段，同时结构和润滑情况也影响带宽。在该频段内润滑条件对系统模态参数有较大的影响，而在该频段之外模态参数受润滑的影响不大。刚度越低的情况下，模态参数受润滑影响的阶数越多。

2.2 转速影响分析

为了研究转速对模态参数的影响，分别将径向载荷和润滑剂黏度设置为2 kN和0.012 Pa·s。如图3所示，速度范围为296～5 296 r/min，对应的Sommerfeld数为0.024～1.24。随着转速的增加，固有频率从约 710 Hz 增加到 830 Hz，阻尼比在转速为1 000 r/min时最小，随后增加，原因是在Sommerfeld数较大时交叉刚度kyx体现出来。从系统FRF还可以看出，随着转速的提高，敏感频段内固有频率会增大，响应振幅也会增大，直到达到一定值后由于阻尼比的增加而下降。

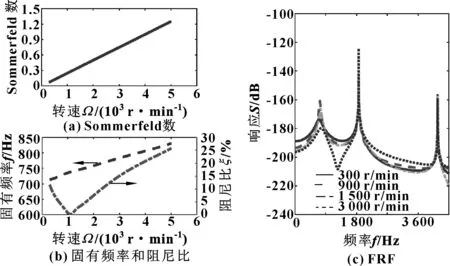
图3 滑动轴承在不同转速下的模态参数

2.3 载荷及润滑剂黏度影响分析

为研究径向载荷对模态的影响，分别将转速和润滑剂黏度设定为496 r/min和0.012 Pa·s，考虑的负载范围为 0.2～4.5 kN，对应的Sommerfeld数的范围为0.055～1.24。如图4(b)所示，增加径向载荷会导致敏感频段内固有频率和阻尼比增加。由图4(b)可看出，随着径向载荷的增加，固有频率上升，响应振幅逐渐降低。

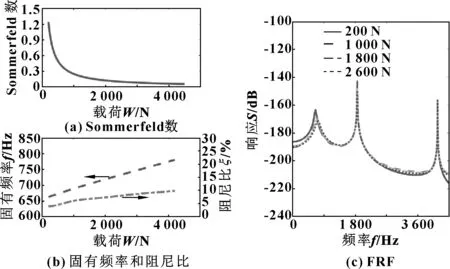
图4 滑动轴承在不同径向载荷下的模态参数

为研究润滑剂黏度对模态分布的影响，将转速和径向载荷分别设置为496 r/min和2 kN。考虑的润滑剂黏度范围为0.004～0.1 Pa·s，对应的Sommerfeld数为0.04～1.075。如图5所示，当使用高黏度的润滑剂时，系统敏感频段内固有频率降低，阻尼比增大，响应振幅降低。

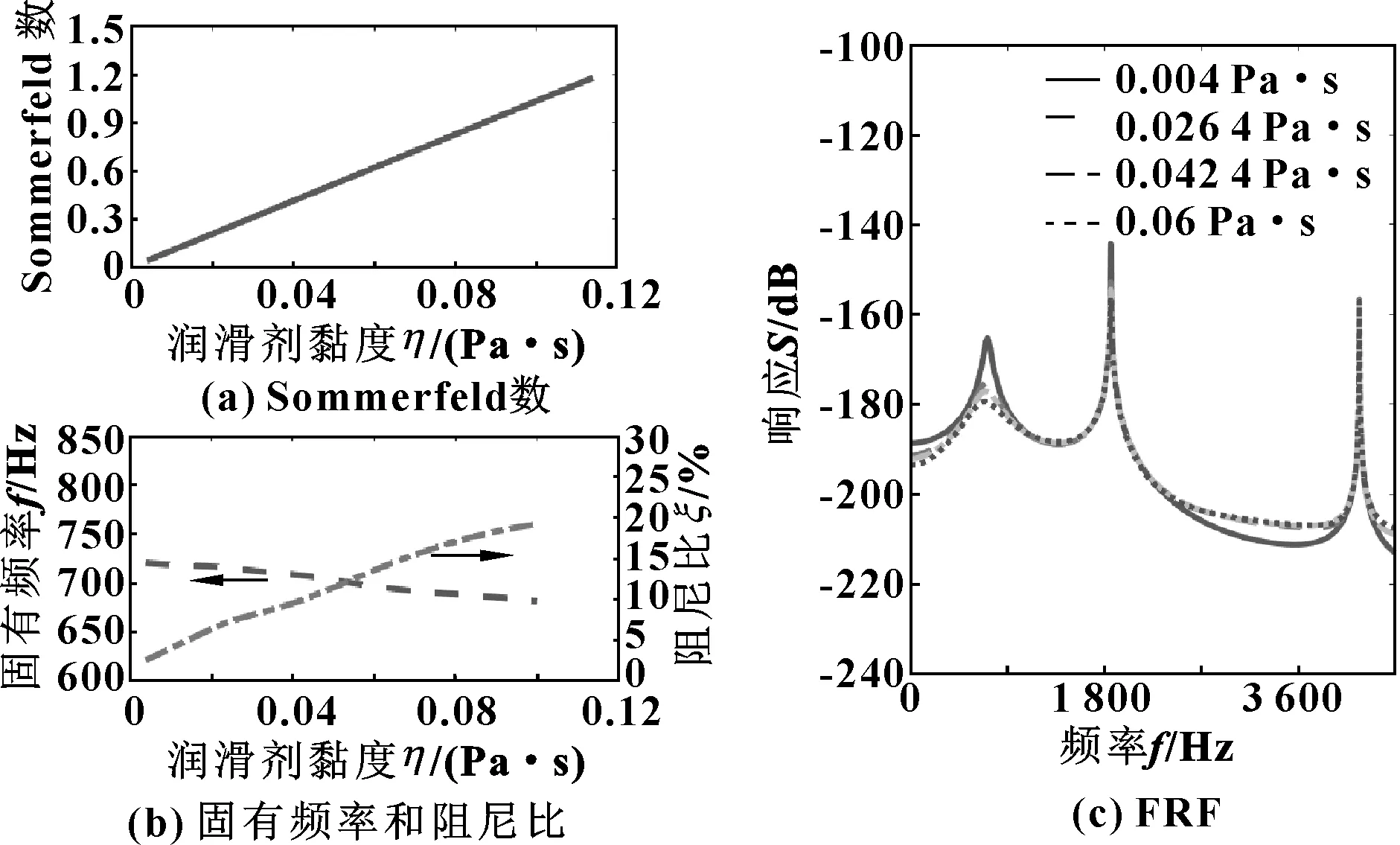
图5 滑动轴承在不同润滑剂黏度下的机械共振

3 实验研究

为了验证上述结果，首先在被测试滑动轴承上进行实验模态分析(EMA)，这样可以估计一下其模态分布情况，然后将该滑动轴承安装在转子轴承试验台上。外壳的宽带振动是在不同的实验条件下获得的，然后用随机子空间法(SSI)确定其模态参数。

3.1 实验模态分析(EMA)

SA35M是一种自对中滑动轴承，如图1(a)所示，表1列出了其几何参数。

表1 SA35M轴承的几何参数

文中用锤击法获得该轴承的模态参数。轴承通过弹性绳悬挂，使用锤子激发宽带响应，然后通过安装在外壳上的加速度传感器获得宽带响应，其频率响应从1 Hz到约20 kHz。重复测试5次获得自由状态下固有频率和阻尼比的均值，列在表2中。

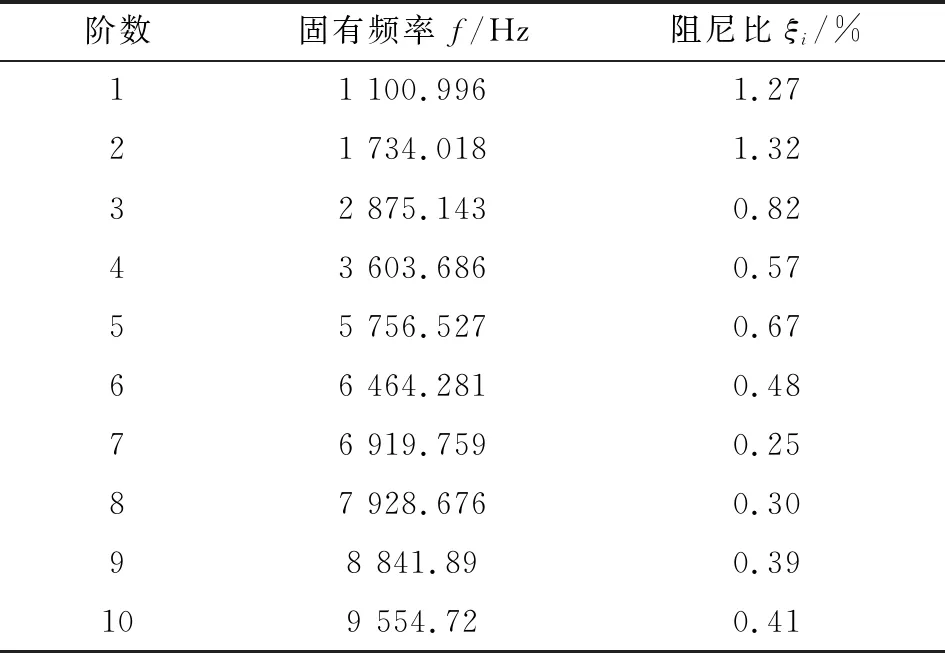
表2 SA35M轴承的模态参数

3.2 转子轴承试验台

如图6所示，三相交流异步电机驱动支撑在一对测试轴承上的转轴旋转，由编码器测量转速，采用液压装置对轴施加径向负载。

实验分别在不同的工作条件下进行。速度分别为600、900、1 200、1 500 r/min，径向负载分别为0.1、0.5、1.0、2.0 kN，润滑剂的黏度分别为5 VG(0.004 5 Pa·s)，15 VG(0.013 5 Pa·s)，37 VG(0.033 3 Pa·s)，46 VG(0.041 4 Pa·s)。

3.3 不同工作条件下的实验信号

从频谱图7(a)可以看出，转速较低时轴承在高于10 kHz时达到固有频率，大致与通过 EMA 获得的模态一致，它验证了微观流固耦合作用所激发的共振现象的出现。由图7(b)可见，振动成分主要发生在2个频率范围内，即低频段(3 000～7 000 Hz)和高频段(7 000～11 000 Hz)内。转速提高会导致激励强度提高，2个频段内固有频率处的振幅也会增大。

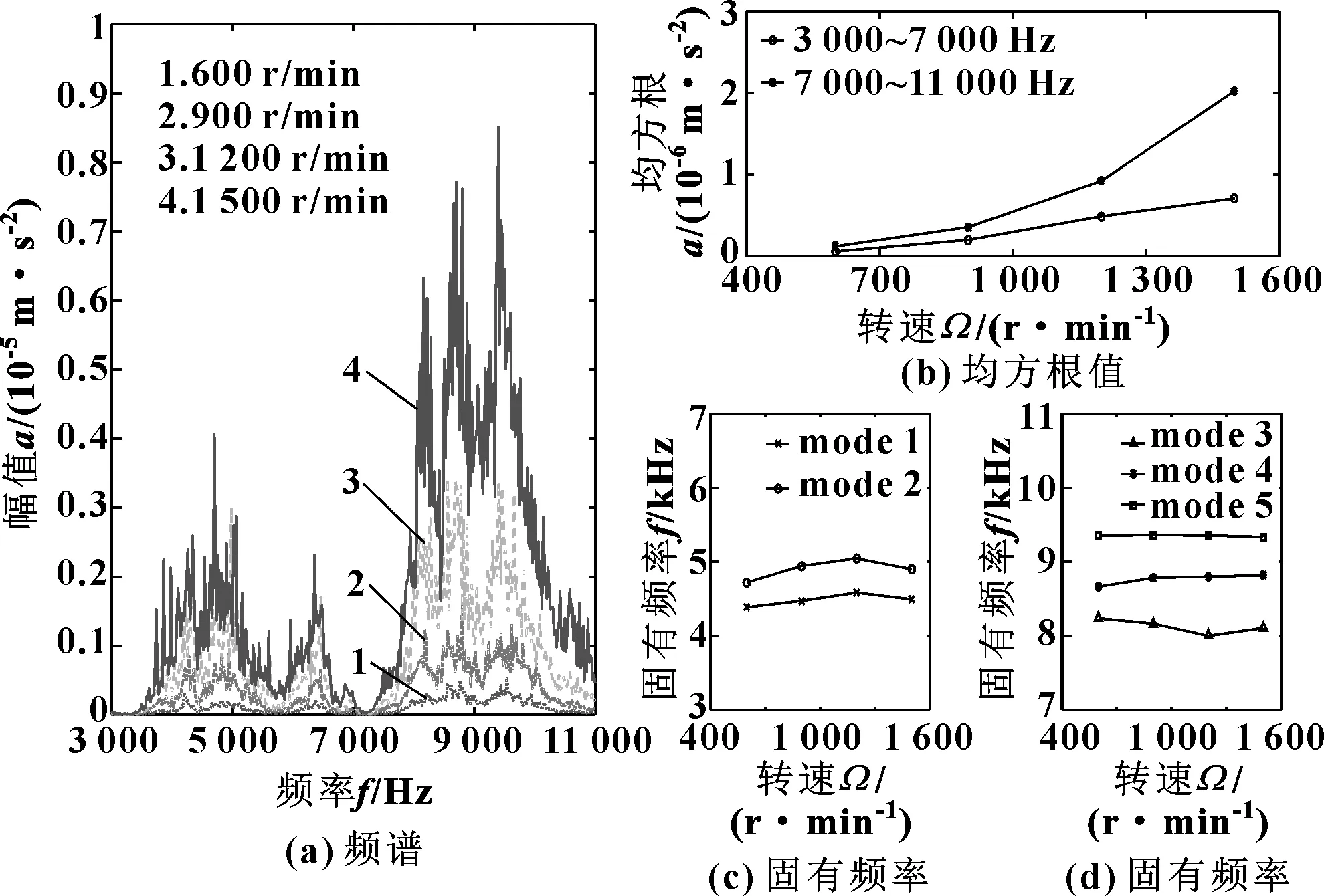
图7 径向载荷1 kN和润滑剂黏度0.033 3 Pa·s条件下，轴承在不同转速下的振动

通过SSI方法获得五阶模态参数，分别对应于EMA中的第3、4、8、9、10模态，这些模态参数更易激发和提取。其中的第3、4阶模态对应的转速和固有频率之间的关系表现出类似的趋势。在1 200 r/min以内，随着转速提高，它们的固有频率逐渐上升。而其他3阶模态参数与转速没有表现出明显的相关性，由此可以推断第3、4阶模态都出现在对流体动力润滑更加敏感的频率范围内。

如图8所示，径向载荷主要影响第3、4阶模态参数，这两阶固有频率分布在对流体润滑敏感的频率范围内。在7 000～11 000 Hz频率范围内，固有频率随着径向载荷增加而振幅的变化并不明显。因此可以看出，高频带内的振幅仅由激励强度决定，当径向载荷加大时，振幅会增大；另外低频带内的振幅同时受到激励强度和系统FRF的影响；较大的径向载荷会导致低频范围内的阻尼比增加，从而降低了相应模态的振幅。

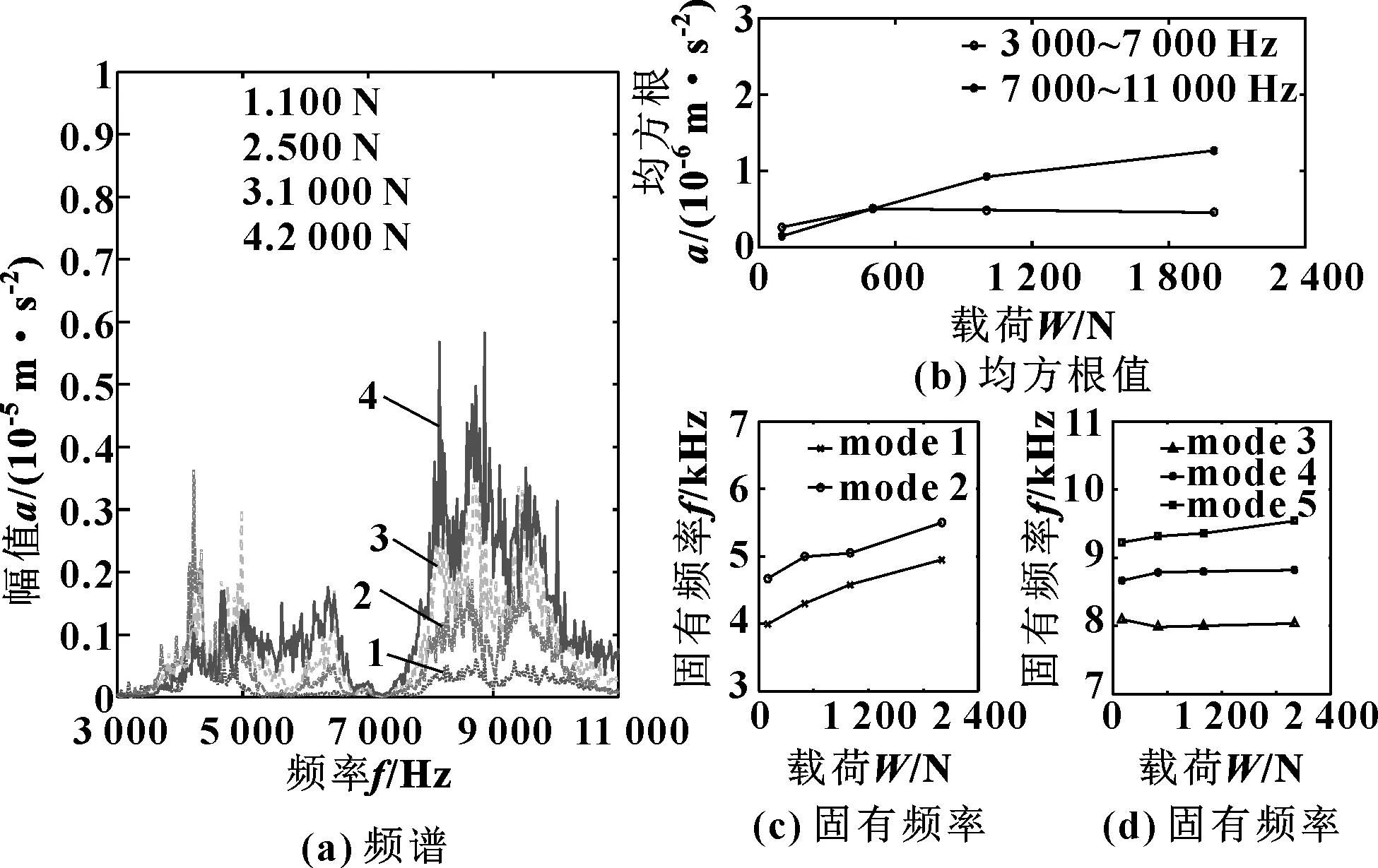
图8 在转速1 200 r/min和润滑剂黏度0.033 3 Pa·s条件下，轴承在不同径向载荷下的振动

如图9所示，由于润滑剂黏度影响水平和竖直方向的激励强度，低频段内两阶模态频率会随着润滑剂黏度的增加而略有下降，而振幅几乎保持不变。

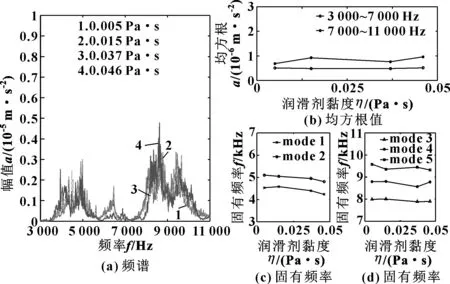
图9 在转速1 200 r/min和径向载荷1 kN情况下，轴承在不同润滑剂黏度下的振动

4 结论

对轴承的随机共振进行了分析，研究了不同操作条件下的激励和模态参数，并进行实验验证。主要结果如下：

(1)系统刚度越高，受润滑影响模态的阶数越少。

(2)随着速度提高，敏感频段内的固有频率增大，响应振幅也增大。速度达到一定的值时由于阻尼比的增加而下降，这个速度转折点由Sommerfeld数决定。

(3)在低频范围内，径向载荷增加会导致固有频率和阻尼比增加，响应振幅降低。

(4)系统使用高黏度的润滑剂时，低频范围内的固有频率降低，阻尼比增大。