圆柱腔小孔节流空气静压轴承动力学性能研究*

李一飞 尹益辉 张 丹

(1.青海民族大学土木与交通工程学院 青海西宁 810007；2.中国工程物理研究院总体工程研究所四川绵阳 621900；3.青海大学土木工程学院 青海西宁 810016)

小孔节流空气静压支承轴承广泛使用于超精密加工或测量设备，如各类超精密光学镜面的加工设备、光刻机等[1-3]。该类轴承的力学性能对相关设备的使用性能有直接的影响，例如，良好的动力学性能有助于提升轴承运行时的稳定性，并可有效提升加工精度[4-5]。轴承力学性能即轴承气膜抵抗载荷的能力，包括静力学性能与动力学性能，静力学性能主要为轴承的承载力与静刚度，反映气膜抵抗静载荷的能力；动力学性能则包括与外激励相关的气膜刚度、阻尼，反映气膜对动载荷的抵抗能力。轴承具备良好的动力学性能，能够更加有效地抵抗动载荷、维持稳定运转，在工程实践中具有重要价值。

对于空气静压轴承的静、动力学性能，目前已有广泛的研究[6-12]。但由于计算、分析的复杂性，目前对轴承气膜刚度、阻尼等动力学性能的认识仍然不足，尚无法有效支撑轴承设计，故目前在设计中，仍以静力学性能为主要设计目标。在动力学性能研究中，将气膜等效为刚度-阻尼系统[13]，其中刚度、阻尼与外激励频率、节流尺寸、运行参数等轴承参数密切相关，可采用有限元、有限差分法或CFD(Computational Fluid Dynamics)数值仿真方法进行计算[2]。对于有限元或有限差分法，首先利用小扰动理论，引入小位移扰动，将雷诺润滑方程分解为稳态与扰动方程，并根据给定的计算区域与边界条件进行求解，即可得到气膜刚度、阻尼。BHAT等[14]使用有限差分法进行计算，讨论轴承尺寸参数、激励频率等对气膜刚度、阻尼的影响。BOFFEY[15]、ARGHIR和MATTA[16]分别针对小孔节流空气静压支承止推轴承与导轨展开研究，求解扰动雷诺方程，分析了气膜的刚度、阻尼性能。

对于轴颈轴承，动力学性能的计算是轴承-转子系统稳定性分析的基础[4-5]，但由于相对止推轴承具有更加复杂的气膜构型，因此针对轴颈轴承动力学性能的分析也更加复杂，不易计算。雷诺润滑方程由流体连续性方程与动量方程简化推出，采用了层流假设且忽略压力、密度沿气膜厚度方向的变化；此外，在基于有限元或有限差分的求解中，通常忽略孔尺寸，并且在流量计算中使用经验流量系数进行修正。这些假设与简化削弱了分析精度，尤其在使用带腔轴承的情况下，更容易引入误差[2]。因此，在轴承气膜的动力学性能计算中，研究人员引入了直接数值仿真方法，基于CFD仿真进行动力学性能计算，由于不需引入上述假设与简化，因此具有更高的精度。CHEN等[17]基于CFD仿真对多孔空气静压支承止推轴承进行分析，讨论了轴承尺寸参数、位移激励幅值、频率等对动力学性能的影响。YU等[18]通过实验校核了采用数值仿真求解轴承动力学性能的准确性。由于轴颈轴承气膜的几何构型远复杂于止推轴承，数值仿真规模激增，LI等[13]结合传统静力学性能计算的工程简化方法与CFD数值仿真，提出了针对轴颈轴承动力学性能计算的ESA-CFD方法，并讨论了轴承参数对力学性能的影响。

气膜的刚度、阻尼与外激励频率密切相关；此外，节流参数、气膜厚度等轴承参数对动力学性能也有显著影响。由于分析的复杂性，目前尚无法获取以轴承参数表示的动力学性能解析表达式，因此，在轴承设计中无法有效考虑动力学性能，不利于轴承性能的进一步提升。

本文作者以圆柱腔小孔节流空气静压支承轴承为研究对象，首先利用CFD数值仿真，结合动网格技术，对轴承气膜刚度、阻尼特性进行分析；其次，基于径向基神经网络模型(Radial Basis Functions Model，RBF)，建立气膜刚度、阻尼与轴承参数的相关性数学模型；最后，基于得到的RBF近似模型，针对轴承气膜的动力学性能展开进一步讨论，尤其讨论了气腔尺寸对动力学性能的影响。

1 轴承几何与数值仿真模型

单孔圆柱腔空气静压支承止推轴承如图1所示，轴承直径D=40 mm，小孔长度l=0.5 mm。其余参数作为变量，其中小孔直径0.1 mm≤do≤0.25 mm、腔直径5 mm≤dc≤8.5 mm、腔深0.02 mm≤hp≤0.12 mm、气膜厚度5 μm≤h≤22.5 μm。在运行中，考虑供气压范围为：0.3 MPa≤ps≤0.65 MPa，外激励频率范围为：10 Hz≤ω≤10 000 Hz。

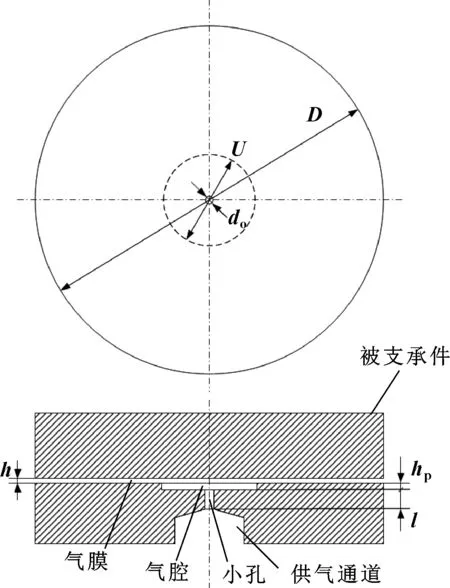
图1 单孔圆柱腔空气静压支承轴承

针对轴承间隙流场进行数值仿真，由于流场几何具有旋转轴对称特性，因此，考虑旋转轴对称二维模型建立流场。边界条件如图2所示：在入口处为压力入口，压力等于供气压力；在出口为压力出口，压力等于大气压；对称轴处设置轴对称边界条件，其余均设置为壁面，为绝热不可穿透无滑移边界。

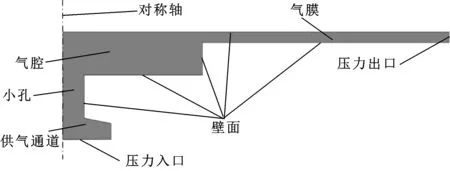
图2 轴承间隙流场边界条件设置示意

在轴承间隙流场中，流动介质为空气，为理想可压气体，黏度满足苏士兰公式[19-20]。由于轴承间隙流场中流动复杂，尤其气腔中的流动为内部射流，空气自小孔进入气腔后撞击止推壁面，形成大量漩涡，因此，在计算中采用湍流。在湍流数值仿真中采用k-ε湍流模型进行计算，该模型广泛使用于轴承间隙湍流流场的模拟中[20]，能较好模拟射流、管流、通道与喷管内流动等内部流场。在数值分析中，还需使用动网格技术模拟外界位移激励，故采用瞬态流计算。

2 轴承气膜动力学性能的数值仿真求解

在轴承设计中，其力学性能包含静力学与动力学性能，静力学性能指承载力、静刚度等，表征轴承气膜抵抗静载荷的能力。动力学性能体现在2个方面，首先为由流场内激励引起的微振动、气锤振动特性；其次为反映轴承气膜抵抗动载荷能力的刚度、阻尼性能。在计算刚度、阻尼时，通常将气膜等效为弹簧-阻尼系统，可采用数值求解雷诺润滑方程或CFD数值仿真的方法进行计算。前者引入简谐时变小位移扰动，首先将雷诺方程分解为稳态与扰动方程，再根据边界条件进行求解；后者在数值仿真中直接施加位移激励，基于气膜的动载荷响应计算刚度、阻尼，具有更高的计算精度。

文中采用数值仿真的方法，计算轴承气膜的动力学性能，采用软件FLUENT数值求解流体连续性方程、动量方程与能量方程[21]，并采用k-ε湍流模型进行湍流模拟。在轴承的动力学性能计算中，给予轴承气膜简谐位移激励，膜厚h的变化满足：

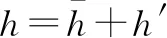
(1)

其中：

h′=hceiωt

(2)

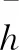
则压力p满足：

(3)

轴承承载力为压力在止推面上的积分，因此，当施加简谐位移激励后，承载力随之变化。若将轴承气膜等效为刚度-阻尼系统，则扰动承载力即为弹性力与阻尼力的合力，在动力学性能求解中，根据输入激励的幅值、频率与输出动承载力的幅值、相位与频率，即可等效求出气膜刚度、阻尼。在数值仿真中施加时变正弦位移激励，使用动网格技术，采用铺层算法，设置分割因子为0.4，合并因子为0.2。在计算中采用瞬态流计算，考虑不同激励频率下气膜的力学性能，为平衡计算效率与精度，在一个激励周期内设置100个时间步，并依此确定时间步长。当位移激励为小扰动时，幅值对于动力学性能的计算结果影响较小[13-14]，故后续仿真计算中，位移激励幅值取为0.1 μm。当气膜厚h=5 μm，小孔孔径do=0.1 mm，气腔直径dc=5 mm，腔深hp=0.1 mm，供气压ps=0.5 MPa时，在不同的激励频率下，动承载力随时间的变化如图3所示。

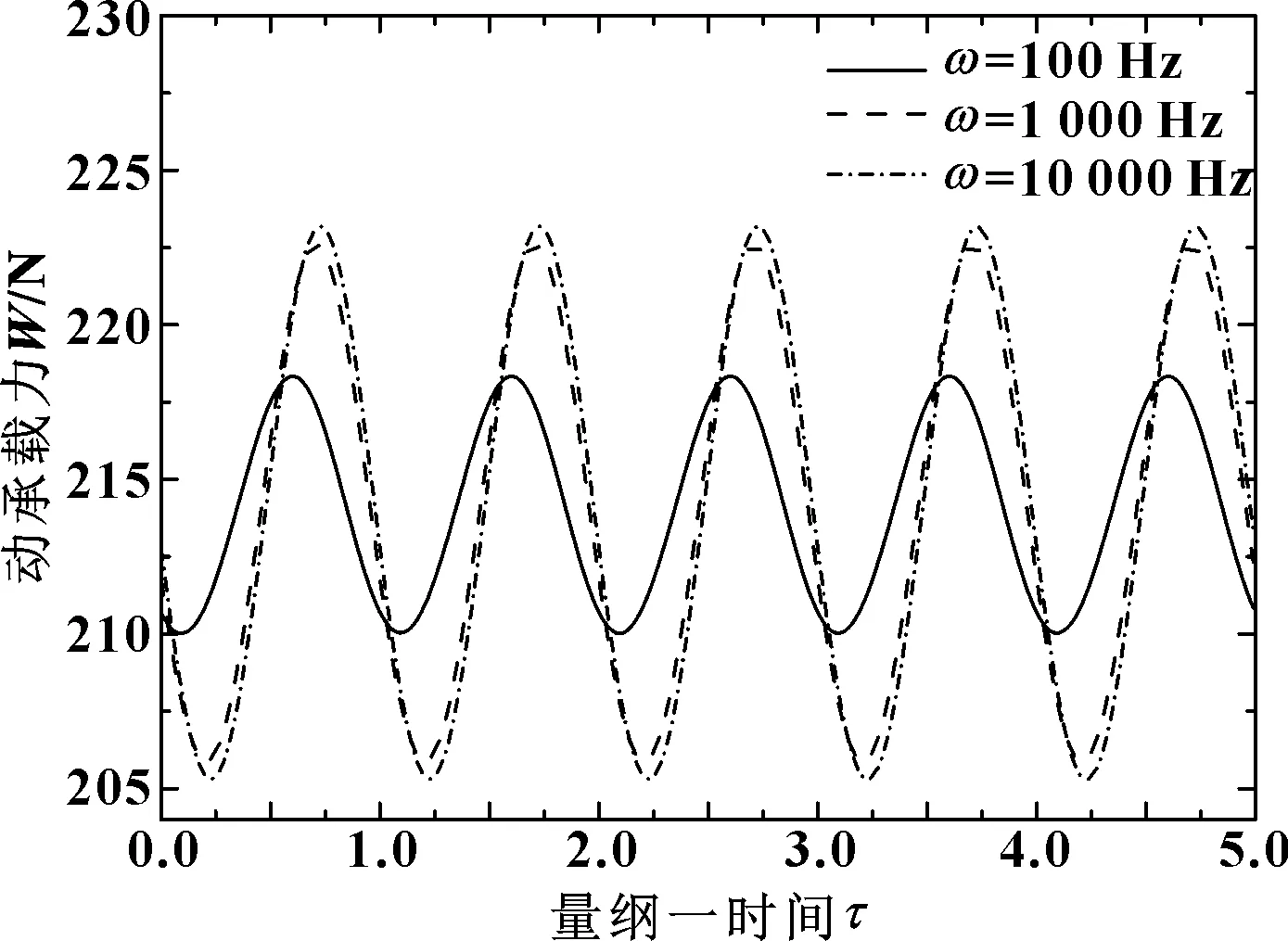
图3 不同激励频率下动承载力随时间变化

由图3可见，当输入正弦激励且频率变化时，动承载力也相应发生变化，其时均值即静承载力保持不变，而动承载力幅值随激励频率增大而增大，相位角发生改变，使轴承气膜在不同激励频率下的刚度、阻尼发生改变，如图4所示。

由图4可见，当激励频率较低时气膜刚度较小，而阻尼较大，随着激励频率增加至某一特定值，刚度开始显著增加，而阻尼相应减小，直至达到另一更大特定值时，刚度的增加与阻尼的减小趋于平缓。形成这种现象的机制在于静压轴承气膜中存在的挤压膜效应。当激励频率较低时，在挤压作用下，气膜内空气有足够时间流出外边界，故刚度接近于静刚度；而激励频率较高时，在挤压作用下，气膜内空气来不及以对应速度流出，气膜刚性变大，导致刚度显著增加，而阻尼相应减小。可见，气膜的刚度、阻尼与激励频率有密切关系。

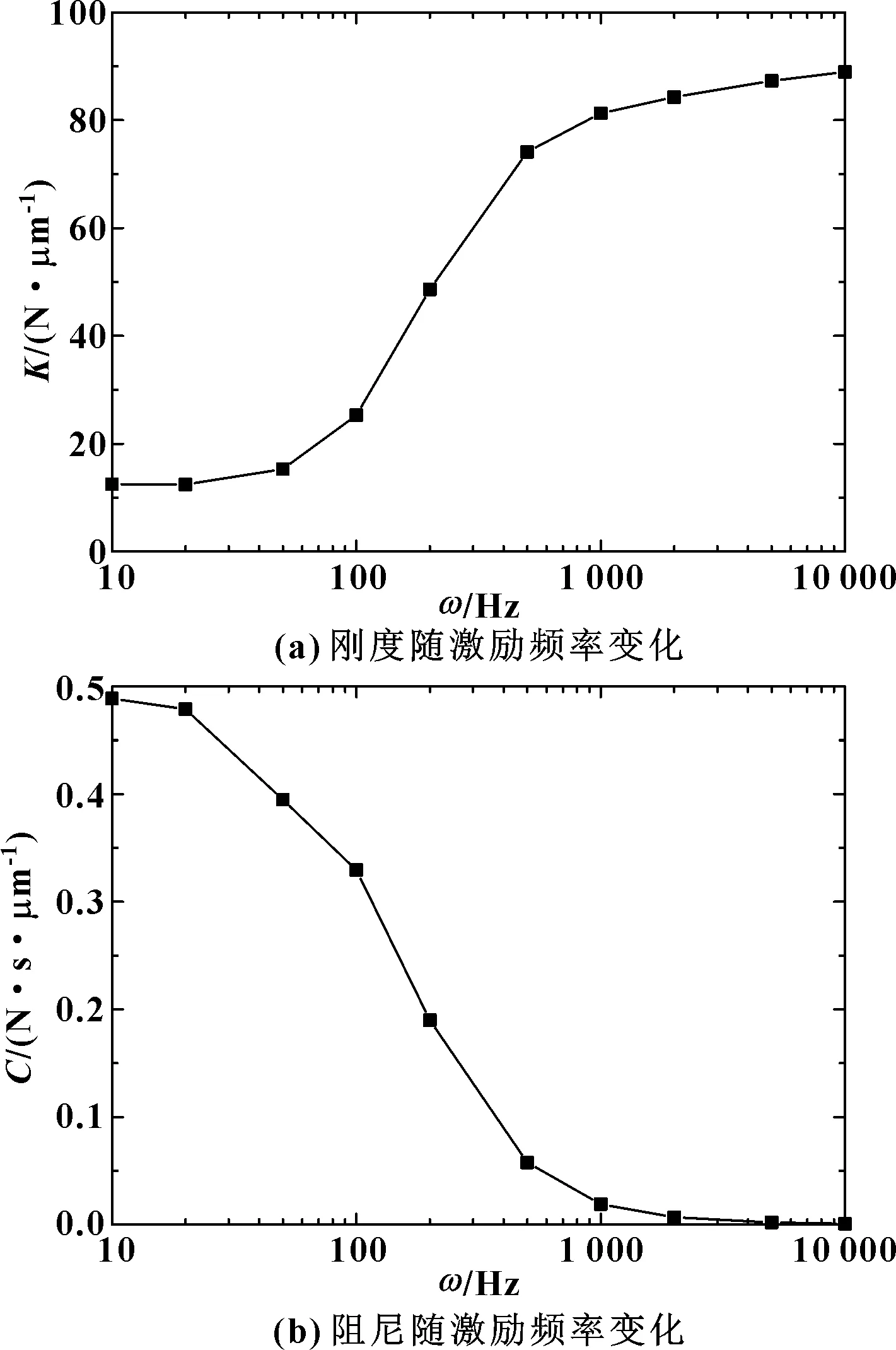
图4 气膜刚度、阻尼随激励频率的变化趋势

为了校核数值分析的准确性，文中采用与文献[22]相同的轴承尺寸进行数值仿真，将时均承载力计算结果与其承载力实验结果进行对比。仍采用瞬态流仿真，激励频率取为1 000 Hz，由数值仿真计算得到时均承载力。如图5所示，数值计算与实验结果最大误差相差8.3%，位于小气膜厚度(h<5 μm)处，其余误差均小于5%，可见数值仿真方法具有足够的准确度[22]。对于空气静压轴承的力学性能，在小气膜厚度下实测值与数值仿真结果间常存在一定误差，其原因为：首先，在小气膜厚度的实测状态下，气膜的厚度尺寸较难设定、测量，易引起误差[23]；其次，在小气膜厚度下，轴承表面粗糙度对力学性能的影响显著增加，也会引起测量误差[24-25]。

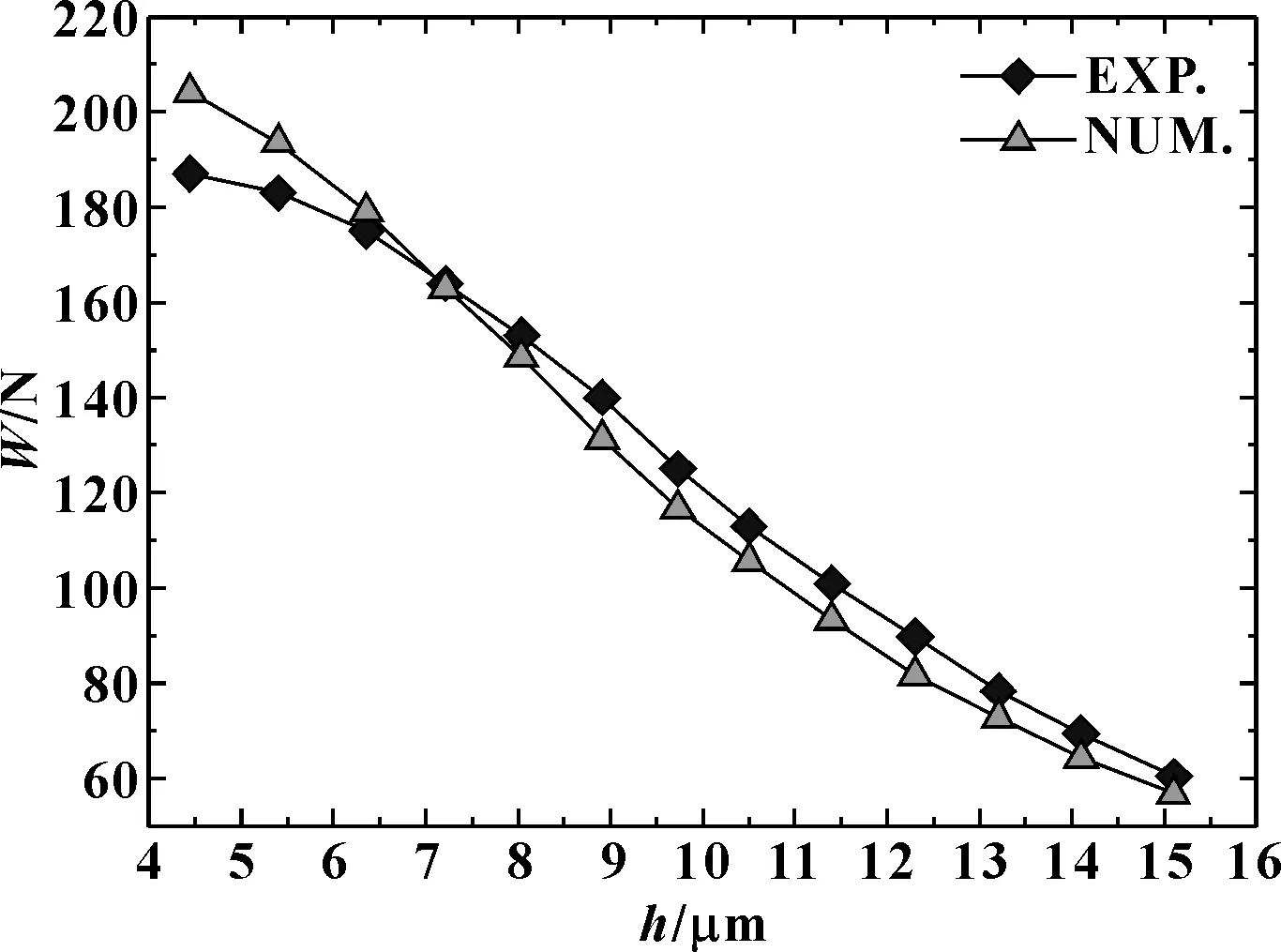
图5 仿真、实验数据对比

3 基于径向基神经网络模型的轴承力学性能研究

对于空气静压支承轴承的动力学性能，目前尚无法获取以轴承参数表示的动力学性能解析解，故尚不能在轴承设计，尤其是优化设计中有效考虑动力学性能的设计。因此，文中基于径向基神经网络(RBF)模型[26]，建立以轴承参数表示的力学性能分析数学模型，并进一步对动力学性能进行研究。

RBF模型广泛应用于工程分析之中，是一种高精度拟合模型[27]。文中利用RBF模型拟合轴承静承载力、气膜刚度、阻尼与轴承参数间的数学模型。其中，静承载力为图3中动承载力的时均值，反映轴承气膜对静载的承受能力，与激励频率无关。因此，考虑轴承气膜厚度h、气腔直径dc、腔深hp、小孔孔径do、激励频率ω，需拟合的力学性能包括静承载力W=W(h,dc,hp,do)，刚度K=K(h,dc，hp,do,ω)，阻尼C=C(h,dc,hp,do,ω)。由于动力学性能关于激励频率有如图4的变化规律，为增加拟合准确性，针对lgK与lgC进行拟合，并且以lgω代替ω，在实际分析中求反函数即可得对应刚度、阻尼。RBF模型插值函数为

(4)

式中：G在拟合中分别表示W、lgK、lgC；x为拟合变量。对于W，x=(h,dc,hp,do)T；对于lgK与lgC，x=(h,dc,hp,do,lgω)T。α=(α1,α2,......,αn+1)T，为未知系数。φj(x)满足：

φj(x)=‖x-xj‖m

(5)

m系数以最小化残差得到。在拟合中采集样本点xi与对应的样本值yi，将其代入式(4)，利用内插法求解式(6)：

(6)

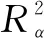
在变量范围内，针对刚度与阻尼，建立5因素、9水平正交表，即L121(95)，针对承载力，建立4因素、9水平正交表，即L121(94)，共进行121组数值仿真，采集样本点并基于RBF模型进行拟合。通过建立近似模型，得到了以轴承参数表示的气膜刚度、阻尼、承载力数学模型。如图6所示为do=0.1 mm、dc=6 mm、hp=0.1 mm、ps=0.5 MPa时气膜刚度、阻尼关于气膜厚度与激励频率的变化规律。可见，由于存在挤压膜效应，使激励频率增加时气膜刚性变大，气膜刚度显著增加，而阻尼减小，在气膜厚度更小时这种变化规律更加明显。基于径向基神经网络模型得到以轴承参数表示的动力学性能数学模型，可详细揭示参数对力学性能的影响特性，为后续讨论轴承气腔尺寸、气膜厚度对力学性能的影响提供了分析基础。

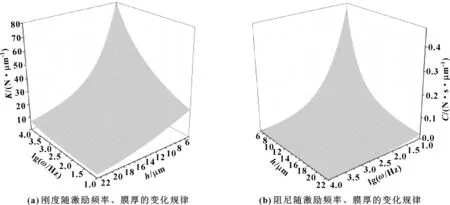
图6 刚度、阻尼随激励频率、气膜厚度的变化规律

4 腔尺寸对轴承气膜动力学性能的影响研究

在工程应用中，较关注气腔尺寸对轴承力学性能的影响，因此，文中对此进行着重讨论。

如图7和图8所示，为分别取小孔孔径do为0.1、0.15、0.2 mm，并取供气压为0.5 MPa时小腔(dc=5 mm、hp=0.02 mm)与大腔(dc=8.5 mm、hp=0.12 mm)轴承刚度、阻尼随气膜厚度、激励频率的变化规律。

由图7可见，当采用小腔时，在高频激励下(ω>300 Hz)轴承刚度大于采用大腔时的刚度。如前所述，由于存在挤压膜效应，气膜刚度随激励频率的增加而增加；对于较低激励频率，气膜内空气在受到激励时有足够时间流出轴承外边界，故刚度较小，接近于静刚度；而对于较高的激励频率，气膜内的空气来不及以相应速度流出，故气膜刚性变大，不易被挤压，导致刚度增加。气腔的存在增加了轴承间隙的气容，由图7可见，对应于给定激励频率，若气腔越小，则轴承间隙气容越小，刚度变化对于激励更加敏感，刚度随激励频率增加更快。同理，当气膜厚度越小时，轴承间隙气容越小，则刚度更大，且随激励频率增长更快。由图8可见，阻尼具有与刚度类似但相反的变化规律。在高频激励下，不论使用大气腔还是小气腔，阻尼均较小；在低频时，随孔径的增加，大腔轴承的阻尼较大，即使用大腔时，在低频，且采用更大的小孔孔径时，具有更大的阻尼。

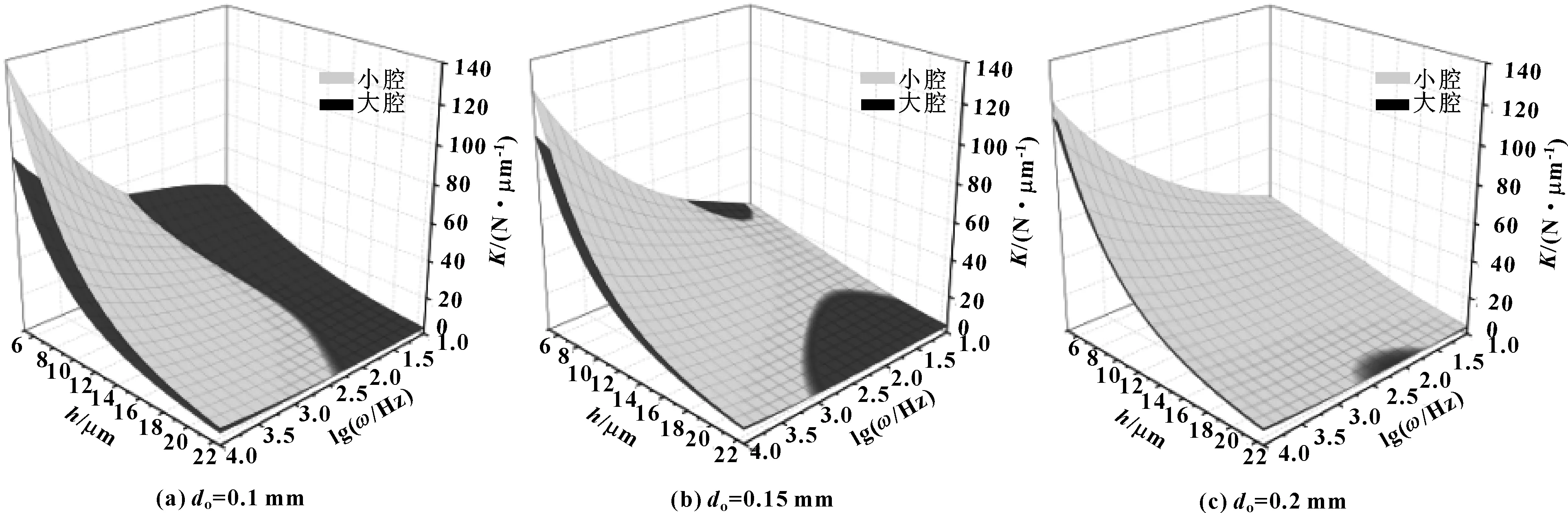
图7 不同腔尺寸下刚度对比

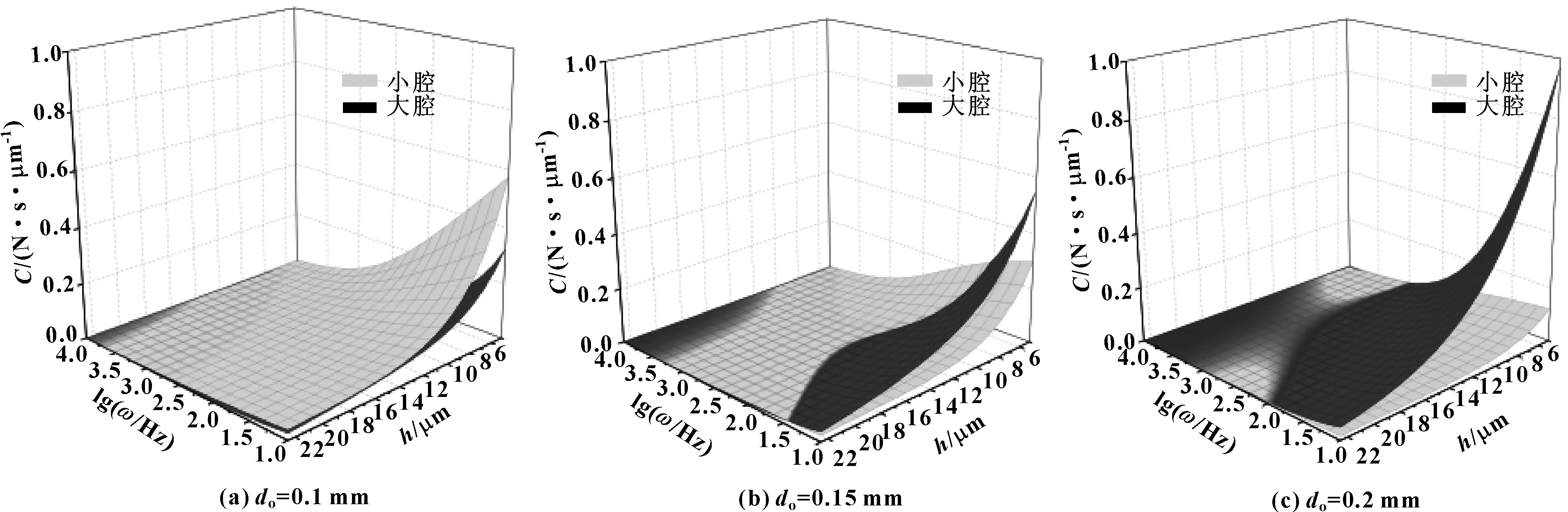
图8 不同腔尺寸下阻尼对比

图9所示为孔径do取0.2 mm时承载力随供气压力、气膜厚度的变化趋势。可见，当气腔变大时，承载力相应提升，与CHEN和HE[19]的研究结论相同，即增加气腔容积可提高承载力。

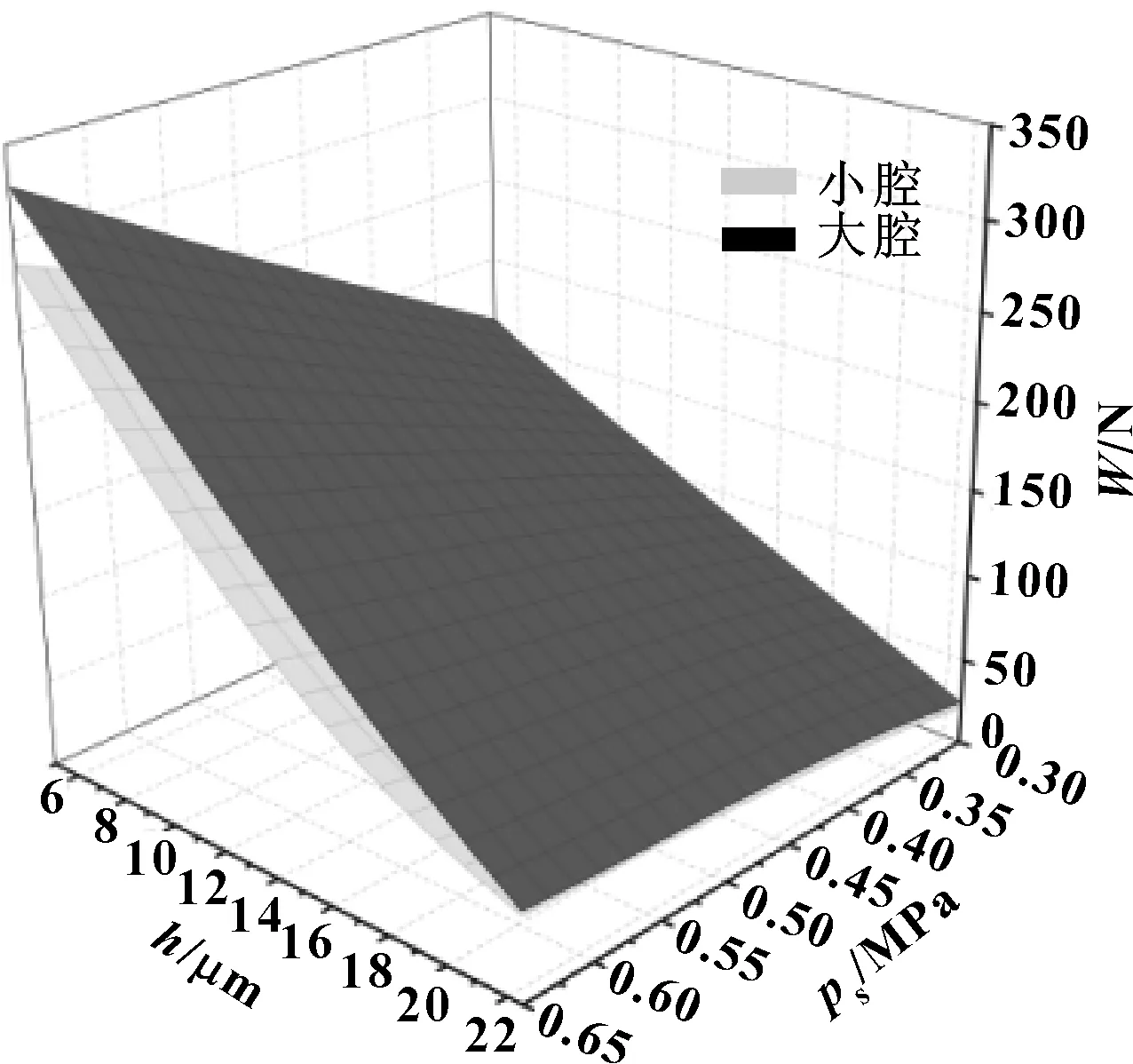
图9 不同腔尺寸下承载力对比

5 结论

(1)首先基于动网格方法进行数值仿真，分析轴承参数、激励频率对力学性能的影响规律。结果表明：当气膜受简谐位移激励时，刚度随激励频率增加而增加，阻尼随激励频率增加而减小，这是由于挤压膜效应而导致。

(2)采用径向基神经网络模型建立轴承动力学性能分析的数学模型，可为轴承力学性能的分析与设计提供有效支撑，尤其相应的近似模型可进一步应用于优化设计，寻求使轴承力学性能最优的设计点。

(3)利用近似模型讨论分析轴承气腔尺寸对力学性能的影响规律，结论表明：当采用小气腔时，轴承承载力较小，但刚度随激励频率的增加更快，而在低频、大节流小孔孔径下，气膜阻尼更小。同样，基于挤压膜效应，当气膜厚度增加时，刚度随激励频率增加的速度减缓。即采用小腔或小气膜厚度时，轴承间隙气容变小，刚度随激励频率的增加变快。