对数修形圆锥滚子轴承接触副径向刚度分析*

杨春辉 王君逸

(华东交通大学机电与车辆工程学院 江西南昌 330013)

高铁轴箱轴承的圆锥滚子轴承中的滚子母线为直线形，存在“边缘效应”。为了消除“边缘效应”，应将母线进行修形。而对数修形滚子可减小“边缘效应”，改善滚子-滚道接触应力分布，改善倾斜滚动体偏载效应，因而得到较多使用[1]。滚子-滚道接触副接触变形及径向接触刚度是轴承负荷分布、动力学特性分析的基础。付圆宁等[2]基于Hertz接触理论和有限元方法分析了圆锥滚子轴承的弹性变形和接触应力等的影响规律；HOUPERT[3]基于 Hertz接触变形计算公式，推导了圆弧形修形圆锥滚子-滚道接触变形的计算公式；王爱林等[4]应用影响系数法推导了圆锥滚子轴承接触变形的计算公式及接触应力分布；CHIPPA和SARANGI[5]基于弹流润滑理论和线接触理论分析了圆柱滚子轴承的接触刚度；刘光辉等[6]采用有限元接触分析方法对圆柱滚子轴承刚度进行分析；吴正海等[7]建立了润滑油膜等效刚度和等效阻尼的圆锥滚子轴承保持架全动力学模型。上述的滚子-滚道接触变形公式均是以点接触计算公式出发进行的，采用数值计算方法求解，需要求解超越方程，对动力学特性分析的效率相当低，实用性不强。

本文作者以Hertz弹性接触理论为基础，给出了对数修形圆锥滚子与滚道之间的接触变形公式，依据弹流润滑理论，建立对数修形圆锥滚子轴承滚子-滚道接触副等效刚度分析模型，为修形圆锥滚子轴承的动力学特性分析提供理论基础。

1 对数修形滚子-滚道接触变形

1.1 弹性接触问题的数值计算方法

陈强等人[8]根据Hertz接触理论对有限长线接触滚动轴承接触变形进行求解，在沿滚子素线方向将可能接触区域Ω，划分为n个矩形单元。设各单元格上的压力pj(j=1,......,n)沿素线方向均匀分布，可得到压力与变形δ关系的线性方程组。

π∑ajhjp0j=Q

(1)

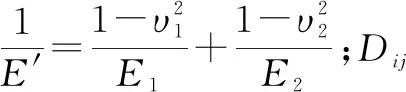
zi为接触表面的初始间距；p0j为单元中心处的最大接触应力；aj为接触半宽。

当Q和Zi已知时，即可解出p0j和δ数值解结果。

1.2 对数修形滚子-滚道接触变形

对数修形滚子母线的一般表达式[9]为

Δ=f1ln[1-f2(2x/le)2]-1|x|≤0.5le

(2)

式中：f1、f2为对数修形参数，f1单位为μm，f2无量纲;le为滚子有效接触长度。

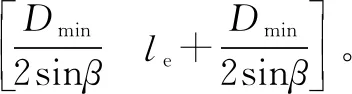
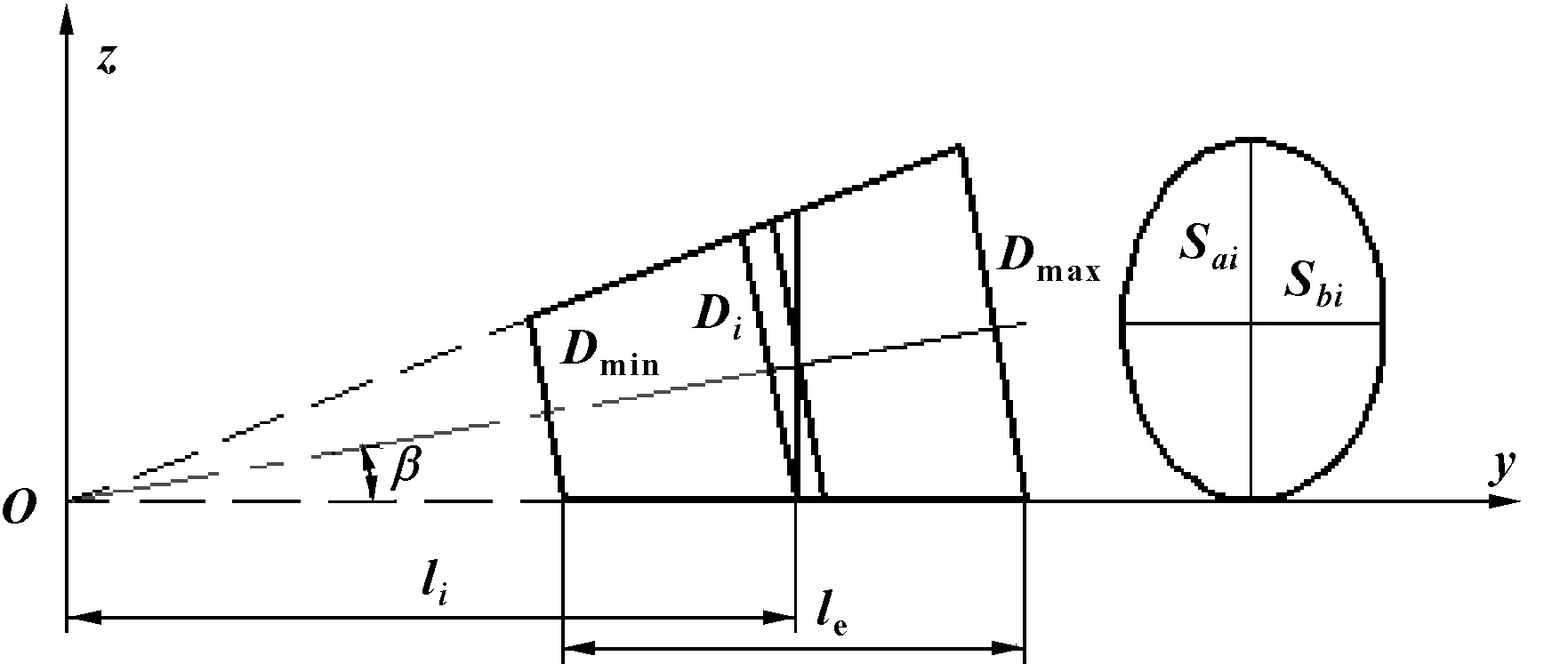
图1 滚子切片

内圈、外圈与滚子接触变形δ1、δ2为

0.58]

(3)

(4)

其中，

式中：Fr为轴承承受的径向力。

各切片处滚子修形量可以看成轴承的径向游隙，切片处内外圈的径向弹性趋近量δ12[11]为

δ12=δ1+δ2+2Δ

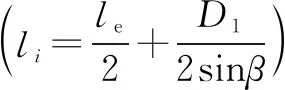
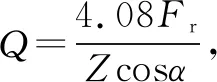
(5)

2 对数修形滚子-滚道接触副油膜厚度的计算

DOWSON根据修形滚子和滚道接触副弹流润滑特性，给出了修形滚子中心油膜厚度公式[13-15]。

(6)

式中：α为黏压系数；η0为润滑油黏度；u为卷吸速度；ker为接触椭圆率，ker=1.033 9(Rv/Re)0.636，Rv为垂直于卷吸速度方向上的等效曲率半径;Ac为载荷油膜厚度系数；Re为等效曲率半径。

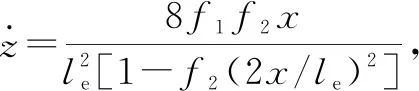
对数修形滚子滚道接触副中心处(x=0)的曲率半径为

3 对数修形圆锥滚子轴承的等效径向刚度

根据弹性流体力学润滑的接触副力学特性研究，将接触副区划分为润滑剂入口区、Hertz接触区、出口区，如图2所示。

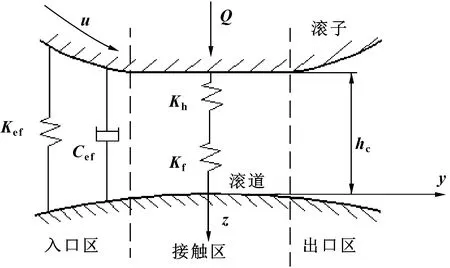
图2 接触副的接触力学模型

两弹性体接触弹性变形时，接触表面将被一层润滑油膜所隔开。弹流润滑下，弹性体接触弹性趋近量δE可表示为

δE=δ+w-h

(7)

式中:w为接触副径向游隙。

根据接触副刚度定义，由式(5)可得到内滚道接触副的Hertz接触刚度为

由式(6)可得到接触区的油膜刚度为

由于接触区的接触刚度和油膜刚度为串联，可到润滑情况下滚子-滚道接触区的等效刚度为

对数修形滚子与滚道接触副入口区的油膜刚度为

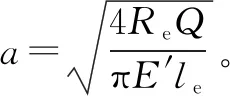
根据图2所示的内、外滚道接触区刚度串并联关系，可到润滑情况下对数修形圆锥滚子轴承内、外滚道接触副的等效刚度为

K1=Kef+KE1

K2=Kef+KE2

内外滚道接触刚度为串联，于是轴承接触副的等效刚度为

4 计算实例及分析

以352 226×2双列圆锥滚子轴承对数修形滚子为例，滚子有效长度为40 mm，滚子半锥角β=0.806°,内圈接触角α=7.75°，滚子小端直径Dmin=22.8 mm，圆锥体等效曲率半径为7.5 mm，对数修形参数f1=4.40 μm，f2=0.997，黏压系数α=2.1×10-8m2/N，润滑油黏度η0=0.02 Pa·s。列车运行速度为v=250 km/h，卷吸速度u=6.8 m/s。轴承的材料选为 GCr15SiMn，弹性模量E=2.06 GPa，泊松比ν=0.3。滚子与内、外圈设置为面-面接触对，摩擦因数设为0.1，轴承外圈全约束，在内圈施加径向载荷为Q=3.5 kN，径向游隙为0。对对数修形圆锥滚子轴承进行有限元静力学接触分析，得到滚子、滚道接触变形分布。

圆锥滚子轴承圆锥滚子-内圈滚道接触变形的有限元分析和理论分析结果如图 3 所示。有限元静力学分析的接触副径向位移与等效刚度计算接触副位移如表1所示，圆锥滚子-滚道接触副的Hertz接触刚度及等效刚度的结果如图4—6所示。

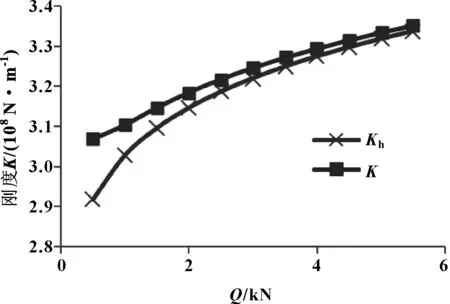
图4 修形滚子-滚道接触刚度随载荷变化

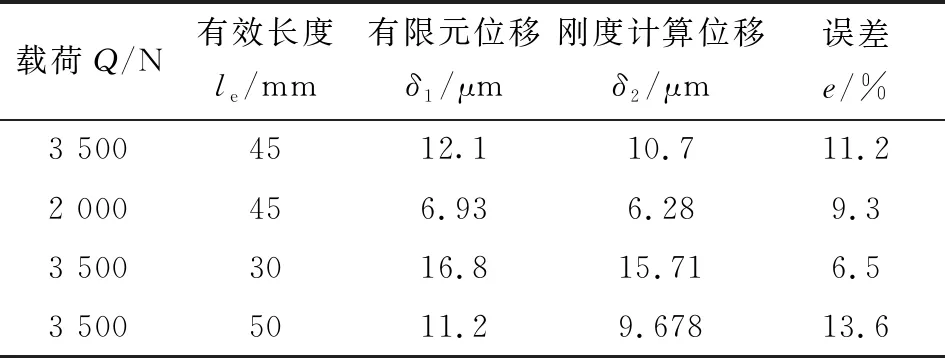
表1 有限元分析接触径向位移与等效刚度计算位移比较

从图3可以看出：接触变形随滚子有效长度le的增大而减小，接触变形随等效半径Re的增加而减小。

有限元分析的径向接触位移与等效刚度计算位移最大误差为14%左右，验证了等效刚度计算结果的正确性。

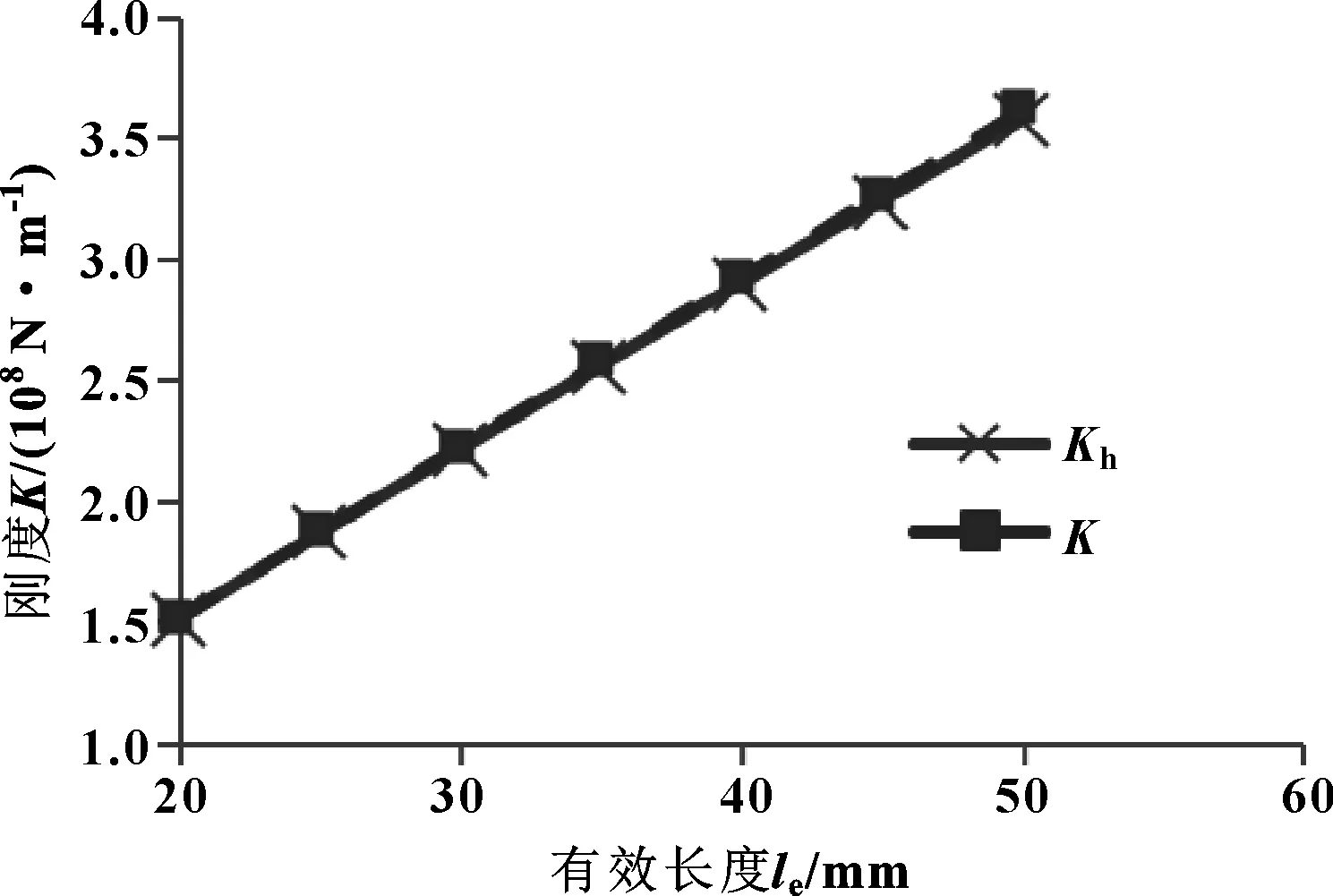
图5 修形滚子-滚道接触刚度随滚子有效长度变化

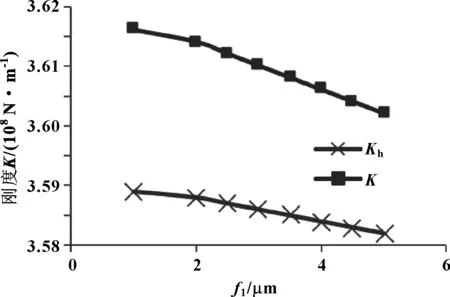
图6 修形滚子-滚道接触刚度随修形量f1变化

从图4—6可以看出：随着接触载荷的增大，对数修形滚子-滚道接触刚度也增大，润滑情况下接触副的等效接触刚度略低于Hertz接触刚度，两者差值随载荷增大而逐渐减小，轻载时油膜刚度对等效刚度影响较大，这是由于径向载荷增大导致油膜厚度会减小，油膜刚度增大所致；随着滚子有效接触长度增大，接触刚度呈线性增大，等效接触刚度与Hertz接触刚度几乎相等，这是由于有效接触长度增大，参与接触面增大，滚子滚道接触变形减小，从而刚度增大，且有效长度对油膜刚度没有影响；随着修形量f1增大，接触刚度减小，但变化微小，可以忽略，这是由于修形量f1增大，垂直于卷吸速度方向上的等效曲率半径减小，油膜厚度增大，油膜刚度减小所致。

5 结论

以Hertz弹性接触理论为基础，针对对数修形圆锥滚子轴承的滚子-滚道接触副接触变形，依据弹流润滑理论和刚度计算方法，建立对数修形圆锥滚子轴承滚子-滚道接触副等效刚度分析模型。结果发现：接触变形随滚子有效长度le和等效曲率半径Re的增大而呈曲线较小；等效接触刚度随着接触载荷的增大而增大，随着滚子有效接触长度增大而呈线性增大，随着修形量f1增大而几乎不变。