银行杠杆及其波动风险对经济增长影响的异质性

杨志辉 杨 嵩

(1.南京大学 商学院，江苏 南京 210093；2.贵州财经大学 数统学院，贵州 贵阳 550025)

一、引言

当前我国经济正从高增长阶段向高质量阶段转化，经济结构调整与增长动力转换矛盾较为突出，总体上经济增速呈现逐年放缓的态势：2012～2019年我国GDP年增长率从7.9%降至6.1%。受2020年突如其来的新冠疫情影响，2020年GDP同比仅增长2.3%。为应对经济增速的下滑，2020年货币政策延续了稳健策略，且《政府工作报告》明确提出充分利用好“降准降息”手段，引导提高M2和社会融资的增速，并设定“大型商业银行普惠型小微企业贷款增速要高于40%、贷款余额同比增速力争不低于30%”的指标，这些措施给银行去杠杆以及控制杠杆波动风险带来新的压力，且这种压力又会因为保障经济增长的内在要求而长期存在。实际上，自2008年全球金融危机爆发以来，银行杠杆及其波动风险便成为政府部门及相关学者关注的重点，银行杠杆水平的设定及其波动风险的控制关乎金融稳定以及经济增长目标的实现。因此，深入研究银行杠杆及其波动风险对经济增长的影响以及在不同地区、不同增速之间的差异性，从而为制定相关政策提供借鉴，具有重要理论研究和现实意义。

梳理银行杠杆对经济增长影响的文献发现，国内外相关学者的研究思路主要沿着两条路径：一条路径是通过银行信贷的渠道来研究银行杠杆对经济增长的影响(促进或是抑制)；另一条路径是通过金融风险来研究银行杠杆率波动对经济增长的影响(金融安全)。早期学者Rioja和Valev、Shen和Lee 研究发现，金融杠杆总体助推了经济增长，但过高的金融杠杆对经济增长会产生负面影响[1][2]。对于这个观点，后期学者基本上给予了肯定。在金融杠杆对经济增长产生负面影响的具体原因分析上，Wagner和Menzoda 认为，高金融杠杆直接或间接地导致了社会资源的错配，引发了社会过度投资，造成了虚拟经济和实体经济的不匹配，从而给经济增长带来不利影响[3][4]。在金融发展方面，银行是金融体系的主体，影响了社会信贷的派生和收缩速度，决定了社会货币供应水平。银行发展给经济发展输送了“血液”，为经济发展提供了强有力的支撑，以银行为代表的金融深化影响着经济增长的速度和质量。Roulet认为，自2008年全球金融危机后，许多国家认识到了金融风险的危害，加大了对银行去杠杆的力度，这些国家银行杠杆率的下降导致了社会贷款总额显著下降[5]。王连军认为，银行去杠杆的程度主要体现在银行信贷供给下降的速度[6]。刘喜和和王晶晶认为，银行去杠杆导致了政府、企业和个人流动性相对过去变得短缺[7]。在金融风险方面，学者主要从金融顺周期的特性(金融变量围绕某一趋势值波动，顺周期性增强会导致金融变量波动幅度增大，进而使得金融乃至经济运行风险增加)出发，研究金融杠杆及其波动对金融风险的影响。比如，Adrian和Shin通过构建金融机构资产负债表模型，明确提出金融机构杠杆行为具有顺周期性[8]。Baglioni等、Dewally等、汪莉以及王倩等的研究进一步为商业银行杠杆行为具有顺周期性提供了证据[9][10][11][12]。何山和彭俞超对比了中国银行业杠杆率与全球银行业杠杆率均值后发现，尽管2011年之后我国银行业杠杆率出现了明显的下降趋势，但目前仍然高于世界平均水平[13]。Greenwood等以及方意等认为,银行杠杆是银行系统风险的重要组成部分，银行杠杆及其波动会放大金融风险以及增加经济波动[14][15]。我国经济要实现健康持续发展，需要进一步平衡好银行业杠杆率与经济增长之间的关系，探索出银行业杠杆率最优调整方式。

综上所述，尽管2008年金融危机后，学者们对银行杠杆与经济增长关系进行了持续关注，但还存在一些不足，且分析问题的视角有待进一步拓展。首先，银行杠杆和经济增长的关系是怎样的？是线性的还是非线性的？其作用机理有哪些？这些有待进一步明确。其次，学者们主要考虑银行杠杆对经济增长的影响，而对于银行杠杆波动如何影响经济增长的讨论还不充分。最后，一些学者发现银行杠杆对经济增长在空间和时间上存在差异，却没有进一步研究其产生差异的原因。鉴于此，本文构建动态面板数据模型，在分析银行杠杆对宏观经济增长影响的同时，探索银行杠杆波动对经济增长的空间异质性。本文可能的边际贡献在于：第一，在研究银行业杠杆水平对经济增长影响的基础上，引入了银行杠杆波动指标，分析了银行杠杆波动对经济增长的影响，为相关研究提供一个新的视角；第二，从地域效应及不同经济增速角度研究了银行杠杆及其波动风险对经济增长的异质性，从而为政策的差异化制订与执行提供借鉴；第三，研究发现银行杠杆波动风险对经济增长会产生抑制作用，这为银行杠杆波动风险的控制提供理论依据。

二、理论分析与研究假设

银行杠杆对经济增长的作用机制可以分为微观和宏观两个方面，微观作用机制通常对应企业层面，通过企业成本和盈利水平进行传导；宏观作用机制包括消费、需求、风险、债务和周期等多个方面，其相对于微观作用机制，宏观作用路径更为广泛。本文拟从宏观角度探索银行杠杆率及其波动对经济增长的作用机制。本文借鉴Grenier的研究，构建家庭、政府两部门模型，从资本变动角度分析银行杠杆与经济增长的关系[16]。

(一)模型设定

1.家庭部门

假定经济社会由多个以无限期人均消费最大化为目标的理性同质家庭构成，其消费函数C(t)受预算约束的影响。若忽略时间影响，并将人口标准化为1，则家庭效用最大化函数可表达为：

(1)

式(1)中，δ表示贴现系数，效用函数取对数形式。预算约束条件：

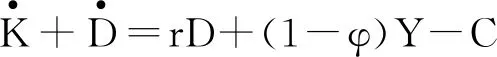
(2)

式(2)中，Y表示总产出(或GDP)；r表示利率；K表示不考虑折旧的私人资本；D表示政府债务；φ表示对总产出所征的固定税率，取值范围为(0,1)。式(2)假设资本变动由政府债务和私人储蓄共同构成。本文将式(2)中的Y设定为Cobb-Douglas生产函数形式，并把公共资本P作为独立的投入要素纳入函数：

Y=AK1-αPα

(3)

式(3)中，A表示技术进步，α∈(0,1)表示公共资本P的产出弹性，1-α表示私人资本K的产出弹性。在均衡条件下，私人资本的净边际产出与利率相等，净产出可表达为：

(1-φ)Y=(1-φ)AK1-αPα

(4)

利率水平通过对私人资本求导得出：

r=(1-φ)(1-α)AK1-αPα

(5)

2.政府部门

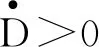
政府部门的约束条件为：

(6)

(7)

鉴于政府部门不仅需要遵守公共财政的“黄金法则”，还需要符合跨期预算约束limt→∞e-rtD(t)=0，则政府债务可表达为：

(8)

(二)模型求解与结果分析

在家庭部门最优化条件下，人均消费增长率gC可表达为：

(9)

同理，私人资本增长率gK可表达为：

(10)

政府债务增长率gD可表达为：

(11)

(12)

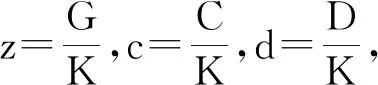
(13)

从式(13)可以看出，均衡增长路径上的经济增长率g与d之间存在非线性的“双倒U”型关系，α=φ时，经济增长率g达到最大值。

通过上述模型分析可知，首先，银行杠杆是银行主体对于私人储蓄和政府债务水平的调节，通过影响私人资本K和公共资本P进而影响经济增长g，其路径是“银行杠杆—私人和公共资本—经济增长”，中间作用变量是贷款成本r、资本产出弹性α和税率φ。其次，银行杠杆对于经济增长g的影响有两种方向，既有正向促进作用也有反向抑制作用，因而银行杠杆对经济增长的总体方向是不确定的。具体而言，银行杠杆水平的上升(下降)使得可用于投资的资本数量P增加(减少)，而投资数量的增加(减少)在一定上能够促进(抑制)经济增长；但是从投资效率和投资质量的角度来看，效果却是相反的，受政策执行期的经济社会发展条件约束，银行杠杆上升(下降)会相对减弱(提高)投资效率和投资质量(α)，增加(控制)投资风险，进而放大(平抑)经济增长的波动，不利于(促进)经济增长。我们用银行去杠杆作为实例进行分析：一方面银行杠杆的下降必然导致银行缩减信贷投放，进而恶化融资环境，导致投资(个人和政府投资)缩减，经济增长下降；另一方面银行杠杆的下降，反映银行在信贷投放过程中更加谨慎，也提高了银行对贷款的监督能力，减少了无效的私人资本(K)和公共资本(P)，使得经济增长更加健康稳定。两方面的综合影响，使得银行去杠杆对经济增长的影响是复杂和不确定的。最后，从局部发展来看，各地区由于经济发展基础、所处产业链地位以及制度环境等差异，导致其总体的投资机会和资本的净边际产出(α)不同，同一货币政策的执行效果也不同，因此中央银行等监管机构在银行杠杠水平的选择上也应强调因时因地制定差异化政策，银行杠杆水平保持适度水平，这样才能保证经济增长处在一个相对较高的水平。在上述理论分析的基础上，再结合其他学者研究的结果(比如Greiner认为银行杠杆对经济增长既有正面的也有负面的影响)[16]，本文提出研究假设1。

假设1：总体上，银行杠杆对于经济增长的影响不确定；局部上，在不同地区和不同经济增速下，银行杠杆对经济增长的影响具有明显的异质性。

经济要保持持续稳定较快的增长，在金融(银行为主体)方面，要综合考虑融资成本和融资后带来的盈利水平(和经济环境及经济周期等有关)，包括和金融有关的消费、需求、风险、债务等多方面因素。从银行主体来看，银行杠杆波动与经济周期的演变为：在经济繁荣时期，银行对于潜在风险的感知较弱，对未来经济增长持乐观态度，对个人和政府的贷款意愿普遍较高，银行内部贷款审核松、门槛低、信贷规模大，继而在银行杠杆指标上表现出较高的特征，由此又推动经济增长，但是在这种经济增长中包含了潜在的风险，或者说是一种不稳定的经济增长，使得经济增长越发膨胀，越偏离最优增长区域，然而在未来某一时刻，当潜在的风险爆发时便会抑制经济增长；在经济萧条时期，银行对于潜在风险的感知较强，对未来经济增长是悲观的，对个人和政府的贷款意愿普遍较低，银行内部贷款审核严、门槛高、信贷规模小，继而在银行杠杆指标上表现出较低的特征，由此进一步抑制经济增长。银行杠杆波动与经济周期作用的内在逻辑在于：银行基于对潜在风险的感知，选择了不同的风险承担水平和不同杠杆水平，进而产生杠杆波动，进而使得经济发展出现波动，其外在表现为经济周期的演变。从投资主体来看，投资主体通过对银行杠杆波动风险的感知，形成资本成本变动预期，并在此预期的指导下形成不同的投资水平和产出水平，但是此预期与实际银行杠杆波动之间存在不匹配，使得投资主体的决策不是实际情况下的最优水平，进而对经济增长产生抑制作用。现实中，投资者(公共投资和私人投资者)一般基于对银行杠杆波动的历史风险与未来风险的感知形成自己投资风险预期，从而表现出不同的投资水平，最终传导到经济增长上，但是银行杠杆波动风险的加大会使得投资的各项资本预期和实际之间的扭曲度加大，资本使用成本加大和收益不确定性加大，使得投资主体的决策偏离实际情况下的最优水平，进而对经济增长产生抑制作用；同样，个人消费也是如此，个人基于银行杠杆波动的历史风险与未来风险的感知，具有不同的消费函数，表现不同时期的消费分配和消费效用，最终传导经济增长上，银行杠杆波动风险的加大会使得个人消费更容易偏离理性决策和最优模式，进而对经济增长存在一定的抑制作用。马勇和陈雨露研究发现，金融杠杆波动会对经济的增长产生负面作用[17]。基于此，本文提出研究假设2。

假设2：银行杠杆波动风险对经济增长会产生明显的抑制作用。

三、样本与变量定义

(一)样本选取与模型设定

在2008年全球金融危机爆发的背景下，世界各地金融与经济的发展受到了重挫，银行业作为我国金融业发展的中流砥柱，为我国金融与经济发展做出巨大的贡献，通过建立良好的金融发展模式保持了我国经济持续稳定增长。本文选用金融危机前后共16年(2001～2016年)我国31个省(市、自治区)的数据，分析我国银行杠杆x及其波动sx对于经济增长y的影响，鉴于银行杠杆波动指标的构造需用到前后两年标准差的移动平均值，因此最后整理为2003～2014年的年度面板数据，并建立如下形式的动态面板模型：

yi,t=α+βyi,t-1+γxi,t+δsxi,t+ηControli,t+μi+εi，t

(14)

式(14)中，被解释变量为经济增长y，核心解释变量分别为银行杠杆x和银行杠杆波动sx，Control为其他各个控制变量，α为常数，μi代表个体效应，εit为残差项，下标i和t分别表示个体和时间，β，γ，δ，η分别为对应回归变量的系数项。

(二)代理变量选取

对于被解释变量(经济增长y)，本文按照通常宏观经济增长变量选取惯例，选用地方年度GDP增长率(记为gdp)作为被解释变量的代理变量，同时后期为了检验结果的稳健性，选用了地方年度人均GDP增长率(记为gdpp)作为被解释变量的辅助变量。

对于核心解释变量(银行杠杆x和银行杠杆波动sx)，已有文献依据《巴塞尔协议III》及中国银监会《商业银行杠杆率管理办法》中对杠杆率的定义(杠杆率=一级资本/调整后的表内外资产余额)，并考虑数据的可获得性，将杠杆率定义为总资产除以权益，同时将银行杠杆定义为杠杆倍数，即杠杆率的倒数[18][19]，该银行杠杆的定义可在整体层面上很好地体现银行业的杠杆水平。然而，对于银行业而言，各银行的分支机构遍布全国各个地区，且各地区银行的所有者权益与总行层面的所有者权益均一致，此时总资产除以权益并不能很好地体现各地区银行业杠杆水平的特征。存贷比作为银行业流动性风险的一项重要指标，不仅可用于监控各地区银行业的流动性风险水平[20]，还可很好地体现各地区银行业的差异特征[21]，并且在我国银行业中，银行存款与贷款仍为银行总负债与总资产的主要组成部分，那么地区银行业的存贷比可近似为地区银行业的资产负债比，而杠杆倍数等于权益除以总资产，又等于1减去资产负债比，即杠杆倍数可近似为1减去存贷比。当存贷比越大，杠杆倍数越小，则杠杆率越高。因此，为更好地反映各地区银行业的杠杆水平，本文选用各地区银行业金融机构贷款余额与存款余额的比值(记为leverage=银行贷款余额/银行存款余额，即存贷比)作为银行杠杆x的代理变量。此外，为分析地区银行杠杆波动风险对当地经济增长的影响，在地方银行业存贷比作为地方银行杠杆指标的基础上，将地方银行业金融机构存贷比的5年移动平均标准差(记为sigmalev)作为银行杠杆波动sx的代理变量。

除了核心解释变量，还需加入可能对经济增长产生影响的因素作为控制变量，本文主要参考马勇、陈雨露的文献，将控制变量分为宏观经济、金融和社会人口状态三个方面[18]。其中，宏观经济变量包括工业化程度(记为ind=工业增加值)、地方政府一般公共预算支出占GDP比重(记为gov=政府一般公共预算支出/GDP)和资本形成率(记为cfr=资本形成总额/GDP)；金融变量包括存款与GDP的占比(记为sag=存款/GDP)和全球金融危机①(记为crisis，虚拟变量，数据年份为2008年全球金融危机时取1，否则取0)；社会人口状态变量为人口增长率(记为popul)。因为这些控制变量对地区经济增长都会产生影响，所以通过对这两方面因素加以控制，能够更好地分析银行杠杆及其波动对经济增长的影响程度。回归变量的定义和数据来源如表1所示。

表1 回归变量定义

为观察这些变量的基本性质，我们将各变量进行了描述性统计(见表2)。

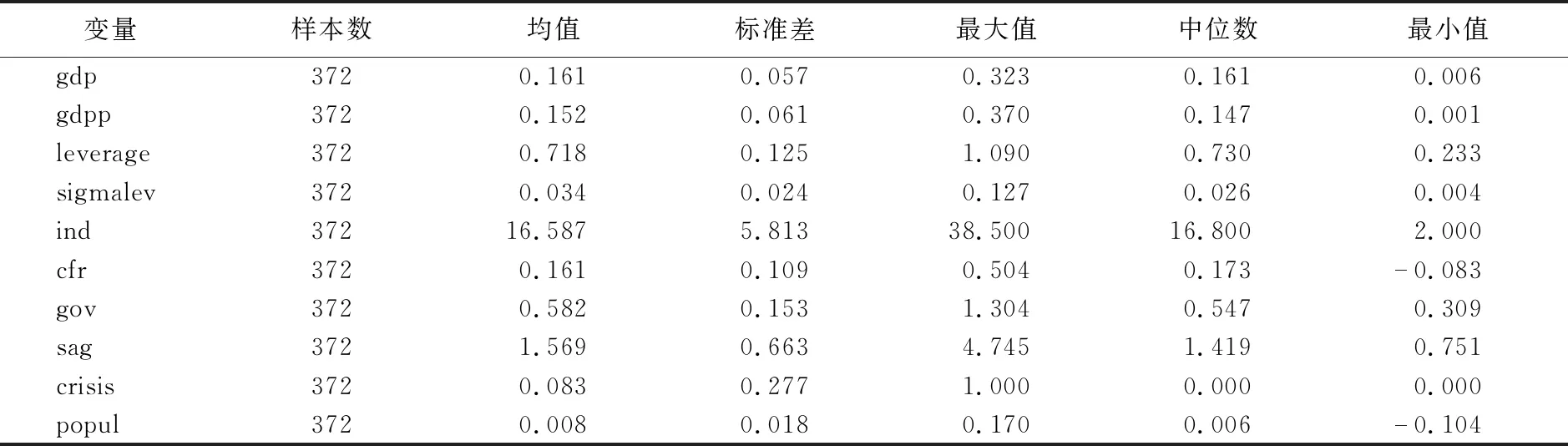
表2 回归变量的描述性统计

由表2的变量描述性统计表可发现，我国各地区GDP人均增长率比GDP增长率的波动更大，且分布更散，说明人均GDP增长率由于受到各地区人口数量限制，使得各地区的增长率差异更大。而银行杠杆率最高达到109%，最低为23.3%，平均为71.8%，这说明我国银行杠杆率多数处于较高水平，另外银行杠杆波动风险主要介于0.4%～12.7%间。

四、实证结果及分析

(一)银行杠杆及其波动风险对GDP增长率的影响

为了分析我国银行杠杆及其波动风险对GDP增长率的影响，下文在动态面板模型式(14)的被解释变量和核心解释变量的基础上，先添加工业化程度、资本形成率以及政府一般公共预算支出占GDP比重作为控制变量，得到模型1，然后，在模型1的基础上，逐次添加存款与GDP的占比、金融危机以及人口增长率，分别得到模型2至模型4，回归结果如表3所示。

从表3的AR(2)检验和Sargan检验可以看出，模型1至模型4都通过了AR(2)检验和Sargan检验，即表示模型的残差项都不存在二阶序列相关和模型过度使用工具变量的情况，说明模型估计过程中的工具变量选择有效，同时模型的估计也是有效的。

由表3的回归结果可以发现，变量leverage与被解释变量gdp在10%的置信水平上没有表现出显著的相关关系，这说明银行杠杆对于经济增长的影响不显著，支持了研究假设1的前部分。而变量sigmalev与被解释变量gdp在10%的置信水平上均表现出显著为负相关关系，这说明银行杠杆波动风险会对经济增长产生抑制作用，支持了研究假设2。

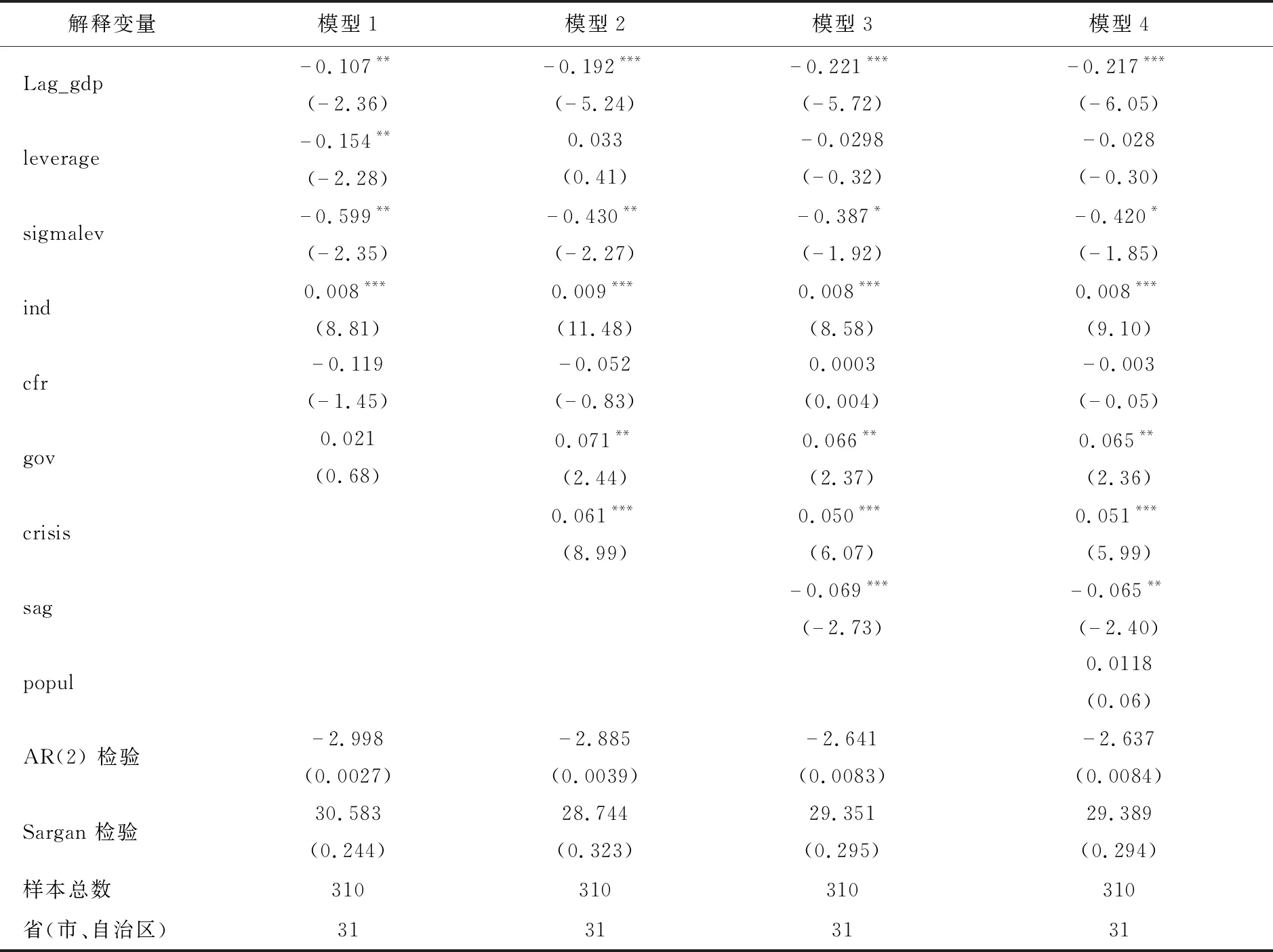
表3 银行杠杆及其波动风险对GDP增长率影响的回归结果

总之，银行杠杆率与经济增长无显著相关关系，而银行杠杆波动风险却会降低经济增长。换而言之，通过提高银行杠杆率并不能有效促进我国经济增长，而有效控制银行杠杆波动风险却可促进我国经济增长。

(二)稳健性检验

从以上回归分析得到结论：银行杠杆率对经济增长无显著影响，而银行杠杆波动风险却会降低经济增长。为检验该结论的稳健性，下文用被解释变量的辅助代理变量(人均GDP增长率gdpp)替代表3中的变量gdp，然后逐次与核心解释变量及控制变量进行回归，得到模型5至模型8，回归结果如表4所示。

从表4的AR(2)检验和Sargan检验也可以看出，模型5至模型8都通过了AR(2)检验和Sargan检验，即表示这些模型的残差项都不存在二阶序列相关和模型过度使用工具变量的情况，说明模型估计过程中的工具变量选择有效，同时模型的估计也是有效的。

由表4的回归结果同样可以发现，变量leverage与被解释变量gdpp在10%的置信水平上没有表现出显著的相关关系，这说明银行杠杆对于经济增长的影响不显著。而变量sigmalev的与被解释变量gdpp在1%的置信水平上均表现出显著为负相关关系，这说明银行杠杆的波动会对经济增长产生抑制作用。

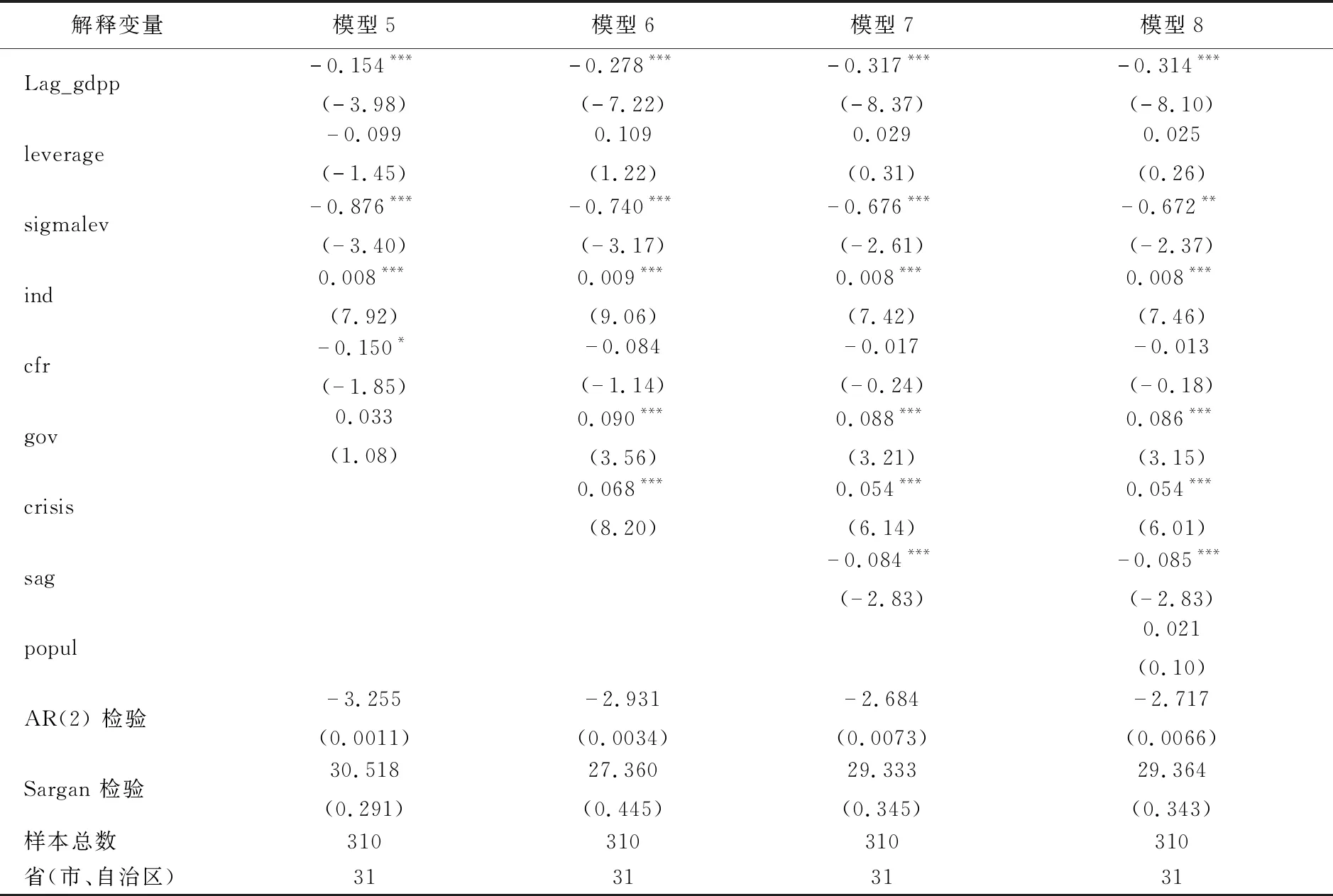
表4 银行杠杆及其波动风险对人均GDP增长率影响的回归结果

以上结论与表3得到的结论相一致，这些进一步验证了表3结论的稳健性，也支持了研究假设1和研究假设2。

五、进一步分析

为了进一步分析我国银行杠杆及其波动风险对经济增长的影响，下文将在前文省际间分析的基础上从三个方面来展开研究。第一，考虑地区杠杆水平及其波动风险与经济增长之间的关系除了地理空降层面的异质性，还可能存在时变性，因此，引入空间杜宾模型(简称SDM)，从空间计量的角度同时讨论了时间及空间上地区杠杆水平及其波动风险对地区经济增长的影响；第二，考虑到我国各个地区差异较大，不同地区的金融环境以及经济发展也有所区别，因此我们针对我国各个省(市、自治区)的不同情况，将我国31个省(市、自治区)按照地理位置进行划分，并针对不同地理区域中的情况进行详细分析；第三，当各地区经济增长不同时，银行杠杆松紧政策对经济的影响也会不同，因此，我们接着依据各地区2003～2014年各省(市、自治区)的年均GDP增长率，将其划分为三个不同经济区域②，然后针对不同经济区域的情况进行讨论。

(一)时变效应

为分析地区杠杆水平及其波动风险对经济增长的空间影响及时变性，本文选用各省(市、自治区)的省会城市或直辖市间的地理距离矩阵作为空间权重矩阵的参考，为简化模型，暂不考虑跨区域的政策性影响，此时距离相近的省(市、自治区)间的相互影响可能会更大，因此对非零的地理距离求倒数并乘上10000进行放大，使得原空间距离矩阵的取值与各区域间影响力度的大小同向化，然后用同向化后的空间距离矩阵作为空间权重矩阵。当空间权重选定后，基于SDM模型，进行空间面板回归，得到回归结果如表5所示。

从表5的回归结果可知：(1)由于Hausman检验值小于0，因此接受随机效应的原假设，即采用随机效应模型的回归结果进行分析。(2)无论是固定效应还是随机效应，回归结果的Spatial rho均显著，这说明在我国31个省(市、自治区)间地理空间差异显著。(3)由随机效应SDM回归结果可知，在同时考虑空间及时间效应时，在10%的水平下，地区杠杆波动风险对GDP增长会起到显著的抑制作用，而地区杠杆水平对GDP增长的影响不显著，此结论与前文得到结论一致。此外，在1%的水平下，地区杠杆波动风险的一阶滞后项会显著促进GDP的增长，而地区杠杆水平的一阶滞后项对经济增长的影响不显著。这说明，地区杠杆水平对经济增长的影响不存在时变效应，而地区杠杆波动风险对经济增长则存在显著的时变效应，表现为当期的杠杆波动风险可促进下一期的经济增长，但是当期的杠杆波动风险却会抑制当期的经济增长，即在不同区域，银行杠杆及其波动风险对经济增长的影响具有明显的时变性。

表5 银行杠杆及其波动风险对GDP增长率影响的空间时变效应

(二)地理区域效应

为了详细分析我国各个省(市、自治区)的不同情况，本文依据我国31个省(市、自治区)所处的地理位置，将其分为6大区域③，并将各区域的GDP增长率、人均GDP增长率、银行杠杆及其波动风险的均值进行统计，统计表如表6所示。

表6 不同地理区域的统计均值

由表6的统计结果可以发现，6大地理区域中，西北的GDP增长率均值最高，而东北的GDP增长率均值最低，而人均GDP增长率均值最高的地区为西北和西南，华东地区最低。此外，华东的银行杠杆率均值最高，华北的银行杠杆率均值最低，而华北的银行杠杆波动风险最高，华东的银行杠杆波动风险则最低。为直观地观察各地理区域中以上4个指标的差异及各指标间相关关系分布情况，我们给出各地理区域4个指标的散点分布图、GDP增长率与银行杠杆及其波动风险的二维散点分布图(图1)。

由图1可以发现，在不同地理区域，以华北和西北区域的GDP增长率、西南区域的人均GDP增长率、西北地区的银行杠杆以及东北和西南区域的银行杠杆波动风险均呈较高趋势。此外，GDP增长率与银行杠杆及其波动风险会呈现出不一样的相关关系，如：在西南区域，随着银行杠杆率的增加，该地区的GDP增长率整体呈现上升趋势；在西南区域，随着银行杠杆波动风险的增加，该地区的GDP增长率又出现下降的情况。

图1 不同地理区域各指标散点分布、GDP增长率与银行杠杆及其波动风险的二维散点分布图

总之，经济增长与金融环境会随着地理区域的改变而改变，因此，针对不同地理区域，分析银行杠杆及其波动风险对经济增长的影响很有必要，我们将该影响的差异称为“地理区域效应”。为了分析该地理区域效应，本文在模型4的基础上，添加银行杠杆及其波动风险的一阶滞后项，依据不同地理区域筛选出各自的样本，因每个区域回归的个体数小于时间长度，不适合再采用差分GMM方法，所以采用偏差校正LSDV(简称LSDVC)法在不同的区域进行回归，得到回归结果如表7所示。

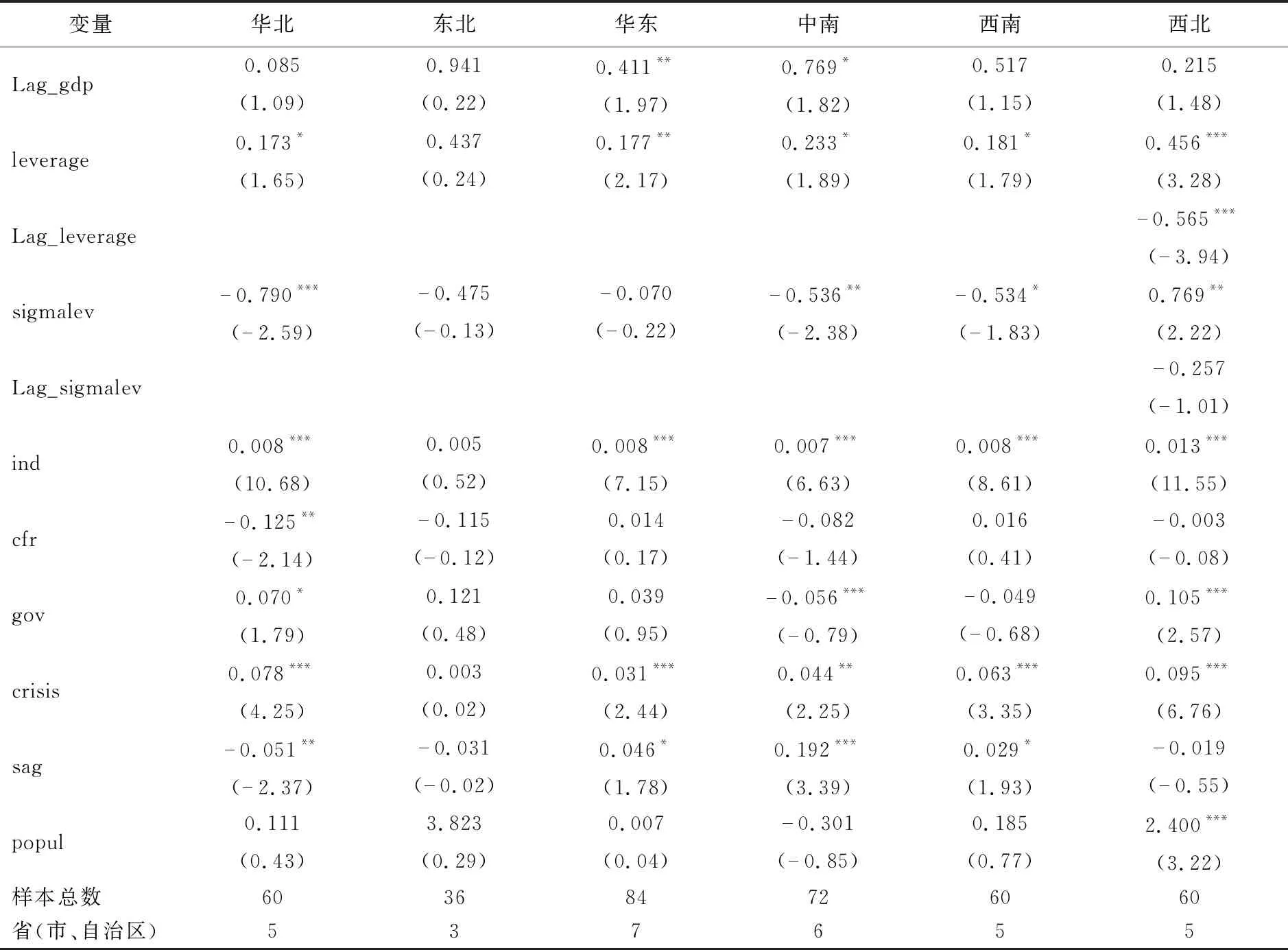
表7 银行杠杆及其波动风险对GDP增长率影响的地理区域效应

由表7的回归结果，可以得到以下两点结论。(1)在西北区域，当期银行杠杆水平在1%的水平下可显著促进当期经济增长，但是当期银行杠杆水平却会抑制下一期经济增长。这说明在西北地区虽然当期银行杠杆水平的提升可拉动经济增长，但是该增长的可持续性并不强，在下一期就会因当期的高杠杆而抑制经济增长。因此，在西北区域放宽银行杠杆限制要求的政策要慎重，需长远考虑。在华北、华东、中南和西南区域，在10%的水平上，当地银行杠杆可显著促进其经济增长，并且均不存在银行杠杆的时变效应。这说明，在华北、华东、中南和西南地区，可以通过适当放宽银行杠杆要求，提升银行杠杆来拉动当地经济增长。然而，因为在东北区域，银行杠杆对经济增长的作用并不显著，所以在东北区域不适合采用“放宽银行杠杆要求”来拉动经济增长。(2)在华北和西南区域，当地银行杠杆波动风险在1%的水平下会抑制其经济增长。在西北区域，当地银行杠杆波动风险在5%的水平下会促进其经济增长，而其他区域中，银行杠杆波动风险对经济增长的影响并不显著。这说明，在华北、中南和西南区域，当地银行杠杆的大幅波动，会提升其流动性风险，并抑制当地经济增长。而在西北区域，正因银行杠杆的变动，降低了高银行杠杆水平对经济增长的抑制作用，反而促进了经济增长，且在各个区域，银行杠杆波动风险对经济增长影响的时变效应均不显著。

为了进一步检验表7得到的结论，本文接着将表7中的被解释变量替换为人均GDP增长率(gdpp)，得到的回归结果如表8所示。

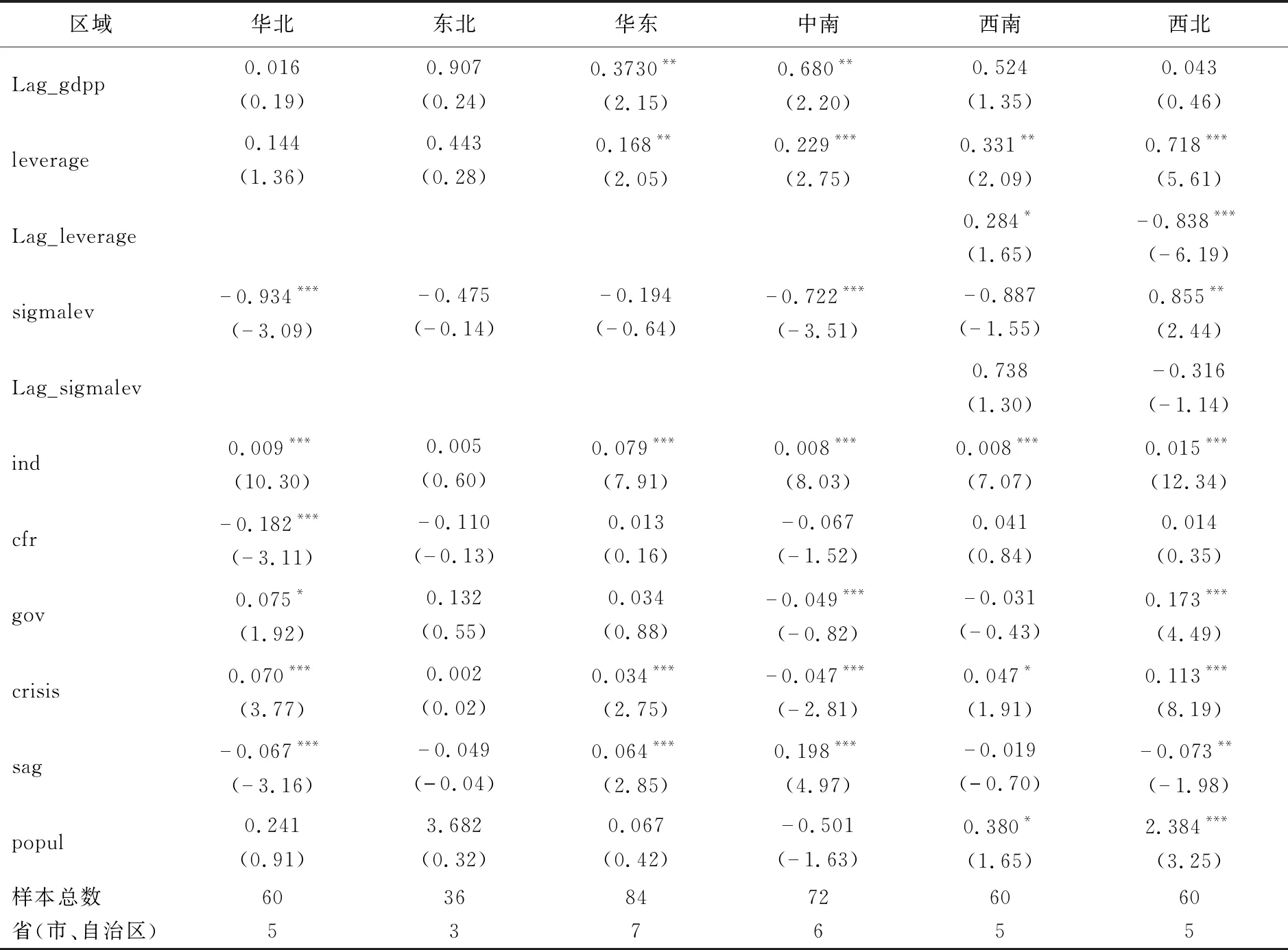
表8 银行杠杆及其波动风险对人均GDP增长率影响的地理区域效应

由表8的回归结果可以发现：在华东、中南、西南和西北区域，当地当期的银行杠杆可促进当期经济增长，但是他们之间的时变效应却表现不同。在华东和中南区域，银行杠杆对经济增长的影响并不存在显著的时变效应，在西南区域，当期银行杠杆可促进下一期人均GDP的增加，而在西北区域，当期银行杠杆却会抑制下一期人均GDP的增加。同时，在其他两个区域，银行杠杆与经济增长间的关系并不显著。此外，在华北和中南区域，当地银行杠杆波动风险在5%的水平下会抑制其经济增长，在西北区域，当地银行杠杆波动风险在5%的水平下会促进其经济增长，而其他区域中，银行杠杆波动风险对经济增长的影响并不显著，且在各区域中，银行杠杆波动风险对经济增长影响的时变效应也不显著。

综合表7和表8得到的结论可以发现，在华东、中南和西南地区，有关部门可以通过适当放宽银行杠杆要求，提升银行杠杆来拉动当地经济增长。但是，在西北地区，当期的高银行杠杆虽然可拉动当期的经济增长 ，但是该增长并不持久，该高银行杠杆在下一期会对当地经济增长产生抑制作用，因此政府在当地采取“高银行杠杆拉动经济发展”的政策时需要慎重。此外，在调节银行杠杆的同时，需重点检测华北和中南区域，由于高的银行杠杆波动风险会抑制其经济增长，因此需加强对该区域银行杠杆波动风险的控制，避免银行杠杆波动对当地经济发展产生不良影响。上述发现进一步支持了研究假设1，即在不同区域银行杠杆对经济增长的影响具有明显的异质性。

(三)不同经济增长区域效应

在经济增速较高的地区，银行机构调整杠杆对经济增长的作用会有所降低，甚至会失效，因此，本文还需进一步针对不同的经济区域进行分析。首先，本文计算出2003～2014年我国31个省(市、自治区)的年均GDP增长率；其次，提取出这31个数据排列后的上三分位点(值为0.1659)和下三分位点(值为0.1548)；最后，定义变量gdparea。当省(市、自治区)的年均GDP增长率小于0.1548时，gdparea=1，表示该省(市、自治区)为经济增长慢区域；当省(市、自治区)的年均GDP增长率大于或等于0.1548并小于0.1659时，gdparea=2，表示该省(市、自治区)为经济增长中区域；当省(市、自治区)的年均GDP增长率大于或等于0.1659时，gdparea=3，表示该省(市、自治区)为经济增长快区域。本文将各经济区域的GDP增长率、人均GDP增长率、银行杠杆及其波动风险的均值进行统计，统计如表9所示。

表9 不同经济区域的统计均值

由表9的统计结果可以发现，三类不同经济发展区域中，经济增长快区域的GDP增长率和人均GDP增长率均最高，经济增长中区域次之，经济增长慢区域则最低。与此同时，经济增长快区域的银行杠杆最高，经济增长慢区域次之，经济增长中区域最低。此外，经济增长中区域的银行杠杆波动风险最大，其他两个区域则大小无明显差异。同样地，为了直观地观察各经济区域的差异，我们给出各经济区域GDP增长率与银行杠杆及其波动风险的二维散点分布图(见图2)。

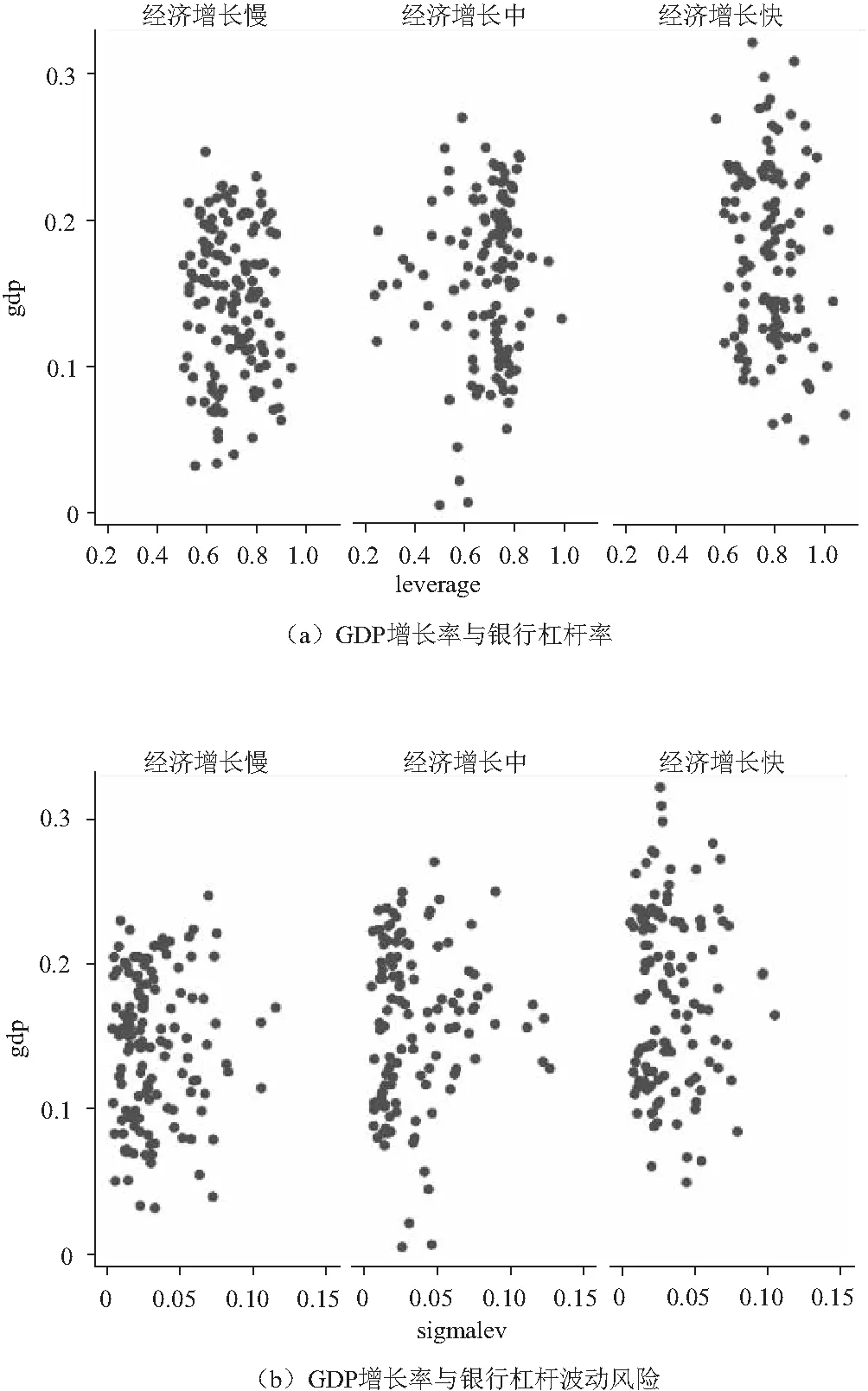
图2 各经济区域GDP增长率与银行杠杆及其波动风险的二维散点图

由图2可发现，在不同经济区域，GDP增长率与银行杠杆及其波动风险的关系存在差异，如：经济增长快区域的GDP增长率分布比经济增长慢区域的GDP增长率分布更散，且前者的GDP增长率整体而言更高。虽然各经济区域间，银行杠杆及其波动风险与GDP增长率之间的关系存在差异，但是仅从图形来看，它们之间的关系并不明显。

因此，为了更详细地分析银行杠杆及其波动风险与经济增长的经济区域效应，在模型4和模型8的基础上，依据不同经济区域筛选出各自的样本，本文分别选用gdp和gdpp作为被解释变量，采用偏差校正LSDV法进行回归，得到回归结果如表10所示。

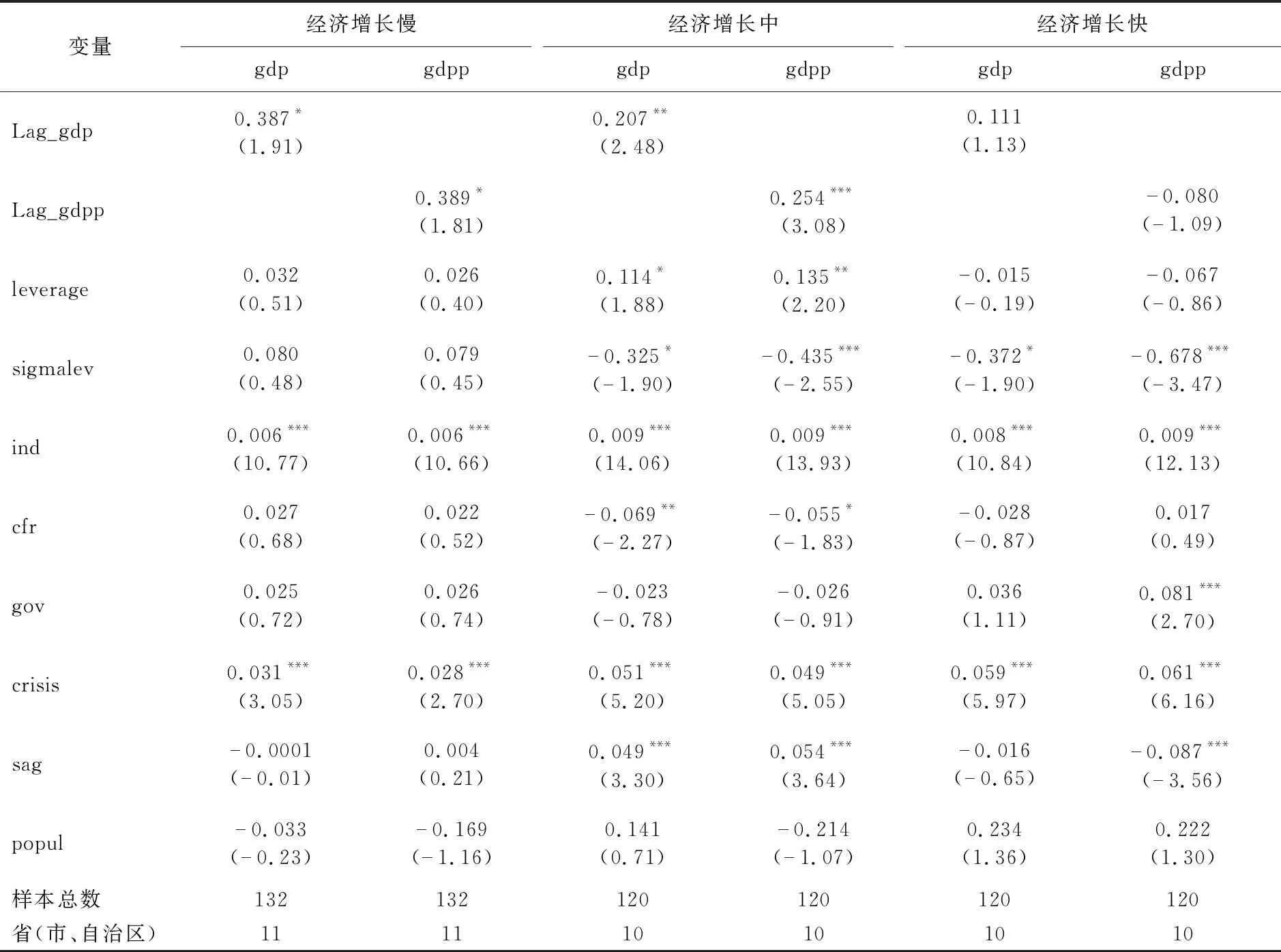
表10 银行杠杆及其波动风险对GDP增长率影响的经济区域效应

由表10的回归结果可以发现以下三点：(1)经济增长慢区域，银行杠杆及其波动风险与经济增长不存在显著的相关关系，即说明银行杠杆对经济增长的促进效应不显著。(2)经济增长中区域，在10%水平上，银行杠杆与经济增长显著正相关，而银行杠杆波动风险与经济增长显著负相关。这说明，在经济增长中区域，银行杠杆可促进经济增长，而银行杠杆波动风险会抑制经济增长。那么，在经济增长中区域，相关部门可适当提高银行杠杆，控制银行杠杆波动风险，进而促进该区域经济增长。(3)经济增长快区域，在10%水平上，银行杠杆波动风险与经济增长显著负相关，而银行杠杆与经济增长不存在显著相关关系。这说明，在经济增长快区域，银行杠杆波动风险会抑制经济增长，而银行杠杆本身对经济增长的作用不大。那么，在经济增长快区域，相关部门需要通过加强控制银行杠杆波动风险，以减少其对经济增长的抑制作用。

综上所述，我国银行杠杆及其波动风险与经济增长存在地理区域效应和经济区域效应。通过整合各地理区域和经济区域的结论还发现，在7个省(自治区)，包括江苏、安徽、山东、河南、广西、四川以及西藏，银行杠杆可以促进该地区的经济增长；在11个省(市、自治区)，包括天津、山西、内蒙古、河南、湖北、湖南、广西、重庆、四川、贵州以及西藏，银行杠杆波动风险会抑制该地区的经济增长。总体上，银行杠杆对于经济增长的影响不显著，不同地域和不同经济增速之间存在差异，但银行杠杆波动风险对经济增长会产生抑制作用，支持了研究假设1和研究假设2。

六、研究结论及启示

本文通过2003～2014年年度面板数据，采用GMM、偏差校正LSDV法以及SDM空间面板模型进行回归，研究了我国银行杠杆及其波动风险对经济增长的作用，同时，进一步通过地理区域和经济区域的划分，发现我国银行杠杆及其波动风险对经济增长存在地理区域效应和经济区域效应。本文得到主要结论如下：

第一，整体而言，我国银行杠杆对经济增长的影响并不显著，这说明银行杠杆不能作为拉动我国经济增长的主要动力。但对不同区域而言，在华东、中南、西南和西北区域，当地银行杠杆的提高可促进当地经济增长；在西北地区，当期高银行杠杆虽然可拉动当期经济增长，但是该增长并不持久，而且，高银行杠杆在下一期会对当地经济增长产生抑制作用。在经济增长中区域，银行杠杆也可促进经济增长。

第二，我国银行杠杆波动风险会显著抑制经济增长。在华北和中南区域，该抑制作用最为显著。同时，在经济增长中和经济增长快区域，当地银行杠杆波动风险对当地经济增长也会起到抑制作用。

第三，通过整合我国银行杠杆及其波动风险对经济增长的地理区域效应和经济区域效应发现，在7个省(自治区)，包括江苏、安徽、山东、河南、广西、四川以及西藏，银行杠杆可促进该地区的经济增长，而在11个省(市、自治区)，包括天津、山西、内蒙古、河南、湖北、湖南、广西、重庆、四川、贵州以及西藏，银行杠杆波动风险会抑制该地区的经济增长。

基于以上结论，本文提出以下政策建议：首先，整体而言，我国银行杠杆波动风险对经济增长会产生抑制作用，需要出台控制银行杠杆波动政策，降低银行杠杆波动风险，特别是以下11个省(市、自治区)，即天津、山西、内蒙古、河南、湖北、湖南、广西、重庆、四川、贵州以及西藏。其次，在7个省(自治区)，包括江苏、安徽、山东、河南、广西、四川以及西藏，相关部门可通过适当提升当地银行杠杆率来促进当地经济增长，但在提升银行杠杆的同时，也要加强对银行杠杆波动风险的控制，特别是河南、广西、四川以及西藏这4个省(自治区)。再次，相关部门应宏观和微观相结合、长期和短期相结合，差异化地、前瞻性地实施银行杠杆的动态管理措施，同时严加防控银行杠杆大幅波动对宏观经济产生的冲击，努力维护金融安全，实现经济增长健康持续稳定。为促进经济高质量发展，中央及地方各相关部门需要进一步平衡好银行业杠杆率与经济增长之间的关系，探索出银行业杠杆率最优调整方式。

本文从空间和时间的角度分析了地区银行杠杆及其波动风险对当地经济增长的影响，发现它们之间存在显著的个体地区效应和时变效应。然而，在构建空间权重矩阵时，仅考虑了各地区的地理距离，未针对国家跨区域的支持政策进行调整，如东部省份对西部省份的定向援助计划就可缩短地理距离，加大被援助区域与援助区域间的影响力度，因此对于如何加入政策性因素进一步构建空间权重矩阵，可作为未来研究的方向。

注释：

①金融危机虚拟变量指的是2008年全球金融危机。

②经济区域划分如下：经济增长慢区域：北京、河北、辽宁、黑龙江、上海、浙江、福建、广东、海南、云南、甘肃；经济增长中区域：山西、吉林、江苏、安徽、山东、河南、广西、四川、西藏、新疆；经济增长快区域：天津、内蒙古、江西、湖北、湖南、重庆、贵州、陕西、青海、宁夏。

③地理区域划分如下：华北区域包括北京、天津、河北、山西、内蒙古；东北区域包括辽宁、吉林、黑龙江；华东区域包括上海、江苏、浙江、安徽、福建、江西、山东；中南区域包括河南、湖北、湖南、广东、广西、海南；西南区域包括重庆、四川、贵州、云南、西藏；西北区域包括陕西、甘肃、青海、宁夏、新疆。