宽量程标准电能表的设计

何建新，李立雄

（1.广东省计量科学研究院，广东广州，510000；2.广州市格宁电气有限公司，广东广州，510000）

0 引言

在电能计量检定工作开展的过程中，经常需要进行宽范围电流测试研究，为了确保测试数据的连续有效性，因此在测试过程中电流不能进行电流档位换挡；而目前国内外主要的标准表为了保证宽量程测量精度以及性价比的需要均设置了多个档位；尽管部分厂家宣称宽量程设计单其只是在一次采用单匝或多匝CT采样，因而一次无需换挡设计，但二次还是进行了3档、4档甚至更多档位设计，在测试过程无可避免的面对档位切换带来的数据损失，特别是动态变化大的电流信号采集无法精准测量，其原理框图如图1所示。

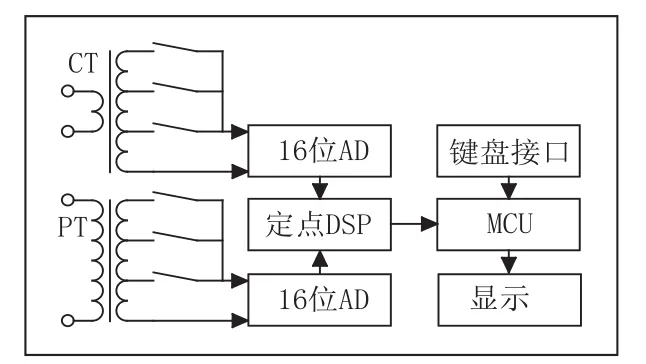
图1 常规标准电能表原理框图

由于电子电路的科技发展，针对标准电能表电流换档及信号采集、处理进行优化设计处理，真正的宽量程标准电能表是可以实现的，采用最新的电子器件，从采样CT、AD、FPGA、DSP、ARM、工控机进行优化组合设计，理论上就可以实现。其原理框图如图2所示。

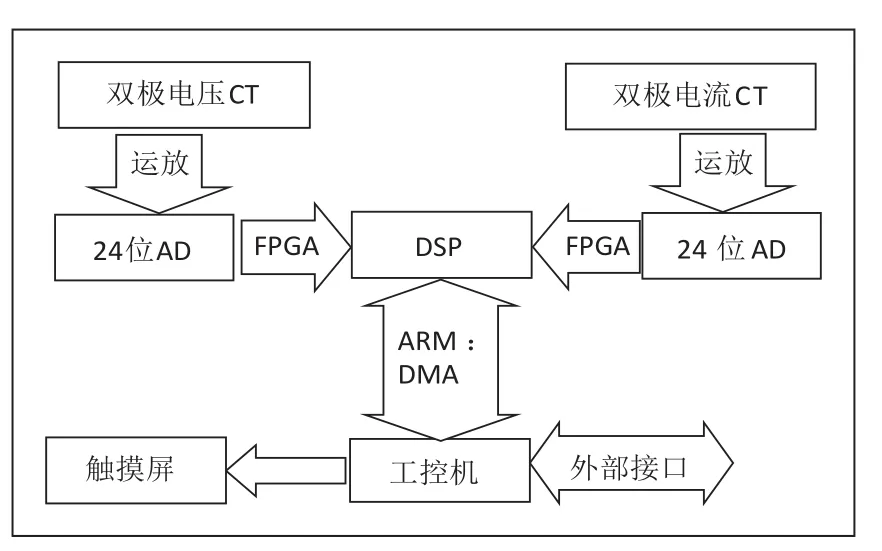
图2 宽量程标准电能表原理框图

1 电流采样电路

电流采样是标准表研制的关键一环，它直接影响整机的性能，是关键中的关键。为了确保电压输入通道的电隔离性，同时确保幅值及相位的准确性；因此电流通道采用双极铁芯电流互感器采样电流信号；通过有源阻抗的矢量电压合成来消除互感器测量误差的方法，带补偿绕组的双级互感器的电流测量原理如图3所示。

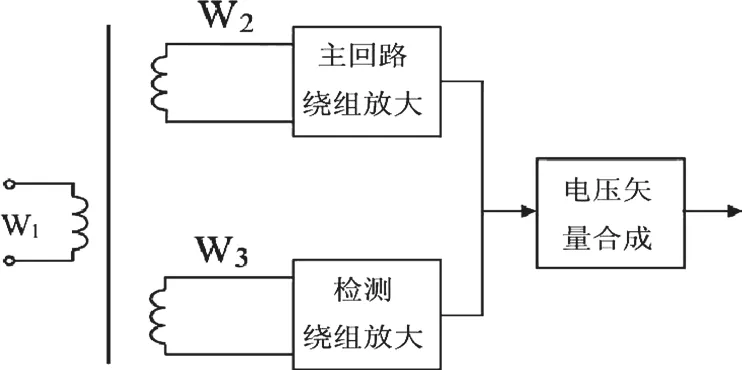
图3 有源阻抗的矢量电压合成原理图

W3为检测绕组，将激磁电流检出，送入补偿电路，通过补偿绕组W2产生补偿电流，使激磁磁通为0，而主回路电流I4可以准确测量出来，即I2从理论上得到公式（1）：

采用检测绕组的电流独立电路检测，使得检测绕组的二次负载用电子电路容易设计为零。当检测绕组的二次负载为零时，互感器的合成误差E在大量程范围内仍然有非常好的线性，使检测绕组铁芯仍处于可测量的线性范围内。

电流采集范围从0.001A～100A，达到10万倍的变化量，为确保0.001A能达到1%的精度，因此需要采集到1uA的信号，也就是采集信号达到千万位数量级，因此选用24位ADC芯片LTC2380-24,2M采样速率，ADC SNR为145dBFS，错码率LSB达到8.4，逐次逼近型SAR采样方式，差分采样输入接口。

采样电路在微信号时达到微安级电流，因此运算放大器选用需要考虑电流或电压的差值较小并且需要予以精确测量低输入偏置电流的运算放大器。使用这些运算放大器时，放大器的输入不会淹没信号。低输入偏置电流运算放大器在电路设计中起着关键作用。例如ADA4625运算放大器，输入偏置电流可低至25pA，满足设计需要。

2 电压采样电路

为了确保电压输入通道的电隔离性，避免电压取样长时间高压高温引起电阻裱花从而影响电压测量采集，同时确保幅值及相位的准确性；因此电压通道采用国内某企业的专利技术设计的双极铁芯电压互感器采样电压信号，达到从30V～480V连续信号幅值采样精度由于十万分之二，相位采集精度优于0.001度。电压互感器变比设计为480V:3V；AD采集芯片采用24位ADC芯片LTC2380-24，由于AD片内基准的稳定性较差，因此需要采用高精度外置电压基准LTC1000，保证电压基准的准确度及稳定度也就保证了A/D采样电路的长期稳定性。

3 信号处理

信号处理电路由FPGA+DSP为核心元件组成；FPGA选用ALTERA公司的Stratix系列高性能、大容量芯片，FPGA是作为连接AD芯片和DSP芯片的桥梁不二之选，采用FPGA作为AD信号读取有着其他芯片无可比拟的优点，由于FPGA具有同步多AD并发读取功能，因此相关联信号采集相位准确度得到很好的保障。原理框图如图4所示。

图4 FPGA+DSP构造框图

DSP负责数据处理及运算以及采集数据输出，选用TI公司TMS320C66X系列DSP，该系列是浮点DSP，浮点计算的速度高，闪光之处是可以通过循环提高运行速度，主频1.0GHz,单核能够达到40GMACS和20GFLOPS；包含2个Viterbi处理器和1个Turbo协处理器，8192个多用硬件队列，支持DMA传输；完全满足前端信号采集的运算量支持。

4 控制电路

控制电路采用独特的ARM架构芯片+工控机组合控制方式，基于ARM核的各种处理器具有高性能、低功耗、低价格，而且具有丰富的可选择芯片，目前市面上型号有好几百种，而且具有广泛的第三方支持。ARM处理器最独特之处是具有支持DMA传输功能，因此设计采用DMA传输方式读取DSP信号处理数据，配合丰富的外设接口支持如以太网、触摸屏等实现人机交互，此方式能够在不影响DSP计算处理的同时进行数据读取，真正实现“一芯二用”。

5 信号处理算法

标准电能测量的信号主要是低频成分，它往往蕴含着信号的主要特征，而高频成分占比相对较小，但它的信息是否能准确的抽取，则决定着信号处理的的细节。因此主要本设计采用快速傅里叶变换和离散小波变换两种计算相结合方式进行数据分析计算处理。

5.1 快速傅里叶变换（FFT）

FFT是用分裂法（Divide & Conquer）的思想，用来优化DFT 计算矩阵相乘的时间复杂度过高这一问题的算法。FFT的过程大大简化了在DSP中进行DFT的过程，简单来说，如果原来计算DFT的复杂度是N*N次运算（N代表输入采样点的数量），进行FFT的运算复杂度是N*lg10(N)，因此，计算一个1,000采样点的DFT，使用FFT算法只需要计算3,000次，而常规的DFT算法需要计算1,000,000次。我们要讨论的FFT也只不过是DFT的一种快速的算法。DFT的运算过程如公式（2）：

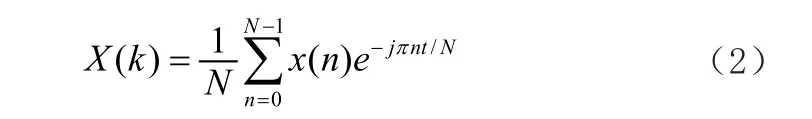
可见，在DSP里进行的DFT，使用的输入值是经过ADC后采集到的采样值，也就是时域的信号值，输入采样点的数量决定了转换的计算规模。变换后的频谱输出包含同样数量的采样点，但是其中有一半的值是冗余的，通常不会显示在频谱中，所以真正有用的信息是N/2+1个点。采用FFT算法能够使用运算效率提高200倍，如图5所示FFT算法和直接计算DFT所需复数乘法次数CM与变换点数N的关系曲线。由此图更加直观地看出FFT算法的优越性，显然，当N越大时优越性就越明显。

图5 FFT算法和直接计算DFT所需复数乘法次数比较曲线

5.2 离散小波变换（DWT）

离散小波变换在数值分析和时频分析中很有用，一维小波变换，二维小波变换小波分解:意义就在于能够在不同尺度上对信号进行分解，使人们在任意尺度观察信号，将信号分解为近似分量和细节分量。

虽然快傅里叶变换可以反映出信号的整体特征，但细节谐波分量的表现形式往往不够直观，并且噪声会使得信号频谱复杂化。在信号处理领域一直都是使用一族带通滤波器将信号分解为不同频率分量，即将信号f(x)送到带通滤波器族Hi(x)中，对信号进行分解、剔除、重构处里来完成信号的降噪，降噪流程图如图6所示。

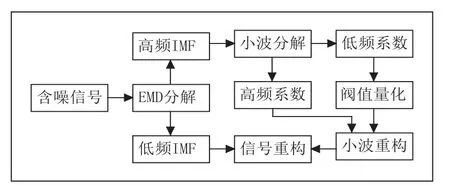
图6 信号降噪算法流程图

小波分析应用在本设计的小信号处理降噪中及电能谐波信号处理中，需要将连续的小波及其小波变换离散化。一般计算机实现中使用二进制离散处理，将经过这种离散化的小波及其相应的小波变换成为离散小波变换（简称DWT）。实际上，离散小波变换是对连续小波变换的尺度、位移按照2的幂次进行离散化得到的，所以也称之为二进制小波变换。

小波分解的意义就在于能够在不同尺度上对信号进行分解，而且对不同尺度的选择可以根据不同的目标来确定。通过不断的分解过程，将近似信号连续分解，就可以将信号分解成许多低分辨率成分。理论上分解可以无限制的进行下去，但事实上，分解可以进行到细节（高频）只包含单个样本为止。因此，在实际应用中，一般依据信号的特征或者合适的标准来选择适当的分解层数。离散小波变换就是对尺度a和偏移b进行离散化，而不是通常意义上的时间离散化。因为离散的间隔小，数据量和计算量就相当大，因此需要研究降低计算量和加快运算速度的算法。通常把尺度a和偏移b取做幂级数的形式表示。

6 结束语

在JJF1245型评大纲的最新要求下，宽量程、高精度的标准电能表将会是今后电能计量检测研究的主要方向及潮流。本设计的实现将为数据测试准确度提供有效准确的数据支持，是一种值得全面推广应用的设计理念。