研究晶须生长基元的一种数学新方法

吴健松，简 艺

(1.广东茂名幼儿师范专科学校 理工学院，广东 茂名 525000；2.岭南师范学院 化学化工学院，广东 湛江 524048)

1 前言

晶须是一种重要的功能材料[1-3]。在晶须的生长技术上，在国外，Jagtap P等[4]采用机械压力作用下锡涂层中晶须的成核和生长动力学。Vianco P T等[5]使用硅作为基底材料，铬作粘附层，铁和锡作蒸发层研究了锡晶须生长过程。Sun M等[6]研究了在长时间压应力作用下锡晶须生长过程，认为锡晶须及其邻近晶粒内部存在位错和层错导致晶须在压应力作用下生长,这是研究金属晶须生长的化学物理行为。在国内，张曼等[7]以 Al(NO3)3·9H2O、H3BO3为原料，Na2SO4做助熔剂，采用熔盐法成功制备出了硼酸铝晶须。杨丽庭等[8]以无水乙醇为介质，且添加有CTAB溶液，用超声波分散法制备了硫酸钙晶须。张宏泉等[9]采用水热合成法制备不同掺杂量的锌离子掺杂HA晶须，发现当 Zn2+掺杂量小于5% 时可合成物相单形貌相对均匀的Zn-HA晶须。这些研究都取得一定的生长技术革新，也表明晶须是一种重要的、有广泛应用的材料，对它的生长技术与生长机制一直以来都是备受关注的。

傅里叶变换，是把看似无规律的信号认为是由一定振幅、相位、频率的基本正弦(余弦)信号组合而得。傅里叶变换的目的就是找出这些基本正弦(或余弦)信号中振幅较大(即加权密度)信号对应的频率，从而找出那些杂乱无章的信号中的主要振动频率特点[17]。傅里叶变换会涉及两个重要的图谱，其一是时域图谱，另一个是频域图谱。简单来说，傅里叶变换就是将时域变到频域。时域图谱是杂乱无章的，很难判断是什么对象在其中起了主要作用。而频域图谱却可通过频谱线(峰)了解到起主要作用的是何对象，这就是变换的主要目的之一。就拿人工可控晶须生长来说，晶须生长体系的pH值随时间的变化图就是一个时域图，在这个图中只能看到无规则的曲线或折线，根本不知道是什么样的对象在其中起了主要的作用。但时域图经过傅里叶变换至频域图后，就可通过对频谱图中那些峰高显著的谱线进行指认。如上文所述，有多少条强谱线，就有多少种对象在起主要作用。傅里叶变换的应用非常广泛，文章不宜尽作解说。在这里，是将傅里叶变换应用在“晶须生长基元的指认”中。研究由金属离子(M)和氢氧根(OH-)组成的生长基元的“种数”。当M与不同的n个OH-组成的多面体[M-(OH)n]生长基元时，就产生不同的“种数”基元，例如当n=3时，组成的[M-(OH)3]就为一种，n=4时，组成的[M-(OH)4]又为一种，依此类推。通常情况下，n可取不同的正整数而组成了多种的基元，但是哪一种占最大比例，起主导作用的呢？这就只能从傅里叶变换得到的频域图中查找了，在时域的曲线图中是根本无法查找的。在这里需指出，傅里叶变换所得的基元“种数”与拉曼光谱测定所得的基元“种数”是完全不同的。傅里叶变换的种数只与n有关，有多少个不同的n就有多少“种”基元，与M无关。拉曼光谱除了与n有关外还与M有关。例如在某晶须生长体系中有镁离子和铝离子，镁与铝都分别与4个OH-组成[M-(OH)4]，那么在傅里叶变换中此种数只有一种，因为n只等于4。但在拉曼光谱就有两种，因为镁与铝是不同的离子，它们与OH-结合时键力常数是不同的，因此[Mg-(OH)4]与[Al-(OH)4]产生的拉曼位移是不同的，因此将有两个拉曼峰，有两种基元。同样，n不同时也必会有不同的拉曼位移峰。傅里叶频谱图是通过频率来区分各分量的，[Mg-(OH)n]与OH-的结合(或解离)，当n不同时将产生不同的频率(f)：

5OH-+M→[M-(OH)5]f1

4OH-+M→[M-(OH)4]f2

3OH-+M→[M-(OH)3]f3

……

因为傅里叶变换的对象是“pH值随时间的变化”，而pH值的增大或减少又只与OH-浓度的增大或减少有关，因此频率(f)只与n有关而与M无关。通常情况[M-(OH)n]的结合(或解离)可以是只有一种形式(n值一定)，也可同时有多种形式(即多个不同的n值)，但只有一种或几种起主要作用，傅里叶变换得到的频谱就可将这种起主要作用的形式通过谱线凸显出来。那些起次要作用的将被“压”在基线上无法凸显。例如上述解离中f2对应的解离是最主要的，就认为起主要作用的是[M-(OH)4]，它对“pH值随时间的变化”起主要作用，在频谱中就只有f2这个谱线(即唯一的主峰)，其他谱线将很弱或不能出现在频谱中，正是基于这一思想，应用傅里叶变换来指认晶须中主要生长基元。经上述的分析可知，这个频率“f”是等同于“几率”。

作者在大量的晶须生长实验中发现，晶须在生长过程中pH值是以小幅度“振荡”的形式变化的，认为这是由于生长基元[M-(OH)n]解离与结合OH-离子所致。解离出OH-时使得体系pH值升高，结合OH-时使得体系pH值降低，这种化学行为是体系pH值“振荡”的主要原因。将pH值“振荡”的函数作傅里叶变换并作图，根据上文所述的傅里叶变换原理，如果在频谱图中只得到1个主峰，就说明pH值振动主要是由一种起“统领”作用的生长基元所致。如果得到两个主峰，那就说明是两个种生长基元化学行为所致，余此类推。文章通过对两个晶须生长体系pH值的“振荡”方程作傅里叶变换，获知晶须生长体系生长基元的存在事实及其组成，这又从数学角度进一步印证了仲维卓、施尔畏等提出的ACP(负离子配位多面体生长基元)机制[16,18-20]及拓展ACP机制[11]的科学性。文章直接以两篇文献[21]和[22]为依托，着重介绍应用matlab实现傅里叶变换的过程及频谱分析方法，这些方法可为人工可控晶须生长、晶体生长领域研究人员提供借鉴。同时文章又是傅里叶变换应用的一种拓展。

2 两个晶须生长体系pH值振荡之傅里叶变换

应用matlab进行傅里叶变换以指认晶须生长基元的方法步骤是(假设晶须生长体系已形成)：第一，拟合晶须生长体系(pH值振荡的)一个周期内pH值随时间变化的函数关系式；第二，编写好matlab程序，将函数关系式(注意要将函数式写成matlab语句式)套入到程序中，运行程序，在输出的频谱图中查看主要谱线也即主峰，一个主峰对应一种生长基元。下面通过两篇文献的数据进行详细论述。

2.1 文献[21]数据的傅里叶变换

对文献[21], 经实验发现，在此晶须生长体系中，浓度随时间的变化呈周期性(t=15 min)的振荡，在一个周期15 min内晶须生长体系pH值(y)随时间(t)的变化规律为如下分段函数所示：

(1)

在(1)式中，t为时间(min)，y为体系pH值。这一关系式在matlab中表达如下：

y=(8.66-0.53*t).*(t≥0&t<4)+(4.0+0.65*t).*(t≥4&t<7)+(8.50).*(t≥7&t<15)

如果应用matlab(2019版，下同)对(1)式作傅里叶变换，得到的傅里叶变换方程F的表达式((2)式)如下：

F=-(433*pi*dirac(w))/50+(pi*dirac(1,w)*53i)/100-(33*exp(1i/w))/5+(539*exp(w*4i) *(pi*dirac(w)-1i/w))/50- (exp(-w*4i)*(pi*dirac(1,w) +1i/w^2)*13i)/20-(exp(w*4i)*(pi*dirac(1,w)+1i/w^2)*53i)/100-(17*exp(-w*7i)*(pi*dirac(w)-1i/w))/2-(11*exp(w*7i)*(pi*dirac(w)-1i/w))/20+(exp(w*7i)*(pi*dirac(1,w)+1i/w^2)*13i)/20+(17*exp(w*15i)*(pi*dirac(w)-1i/w))/2+433i/(50*w)-53/(100*w^2)

(2)

这个经傅里叶变换后得到的(2)式虽然很复杂，但这式子的表达并不是文章所要关注的，之所以将其列出，仅想说明在下文进行傅里叶变换过程得到的频谱峰其实就是从这个方程中“提取”出而已。文章最关注的，是变换得到的频谱图，从频谱图中寻找主峰以获取晶须生长体系中主要生长基元的信息。其实傅里叶变换可绘出多个图像，这里根据需要只绘出两个。其中一个为原始的即(1)式的函数图像，另一个为频谱图，频谱图是文章着重讨论的部分。下文中的图1和图2都是由两个分图组成，A分图都是原始信号图(即上文所提到的“时域图”，这里也就是pH值随时间变化的曲线图，下文用“原信号图”表示)，而B分图都是变换后得到的频谱图(下文用“频谱图”表示)，为方便讨论，下文不再重做交代。为对(1)式实现傅里叶变换并绘出图像，编写如下的matlab代码(“%”后面为注释部分)：

clear all %清除matlab窗口中所有历史记录；

t_s=0.01; %采样周期(但这不是pH值波动周期，而是傅里叶变换采点周期)；

t_start = 0; %起始时间(即pH值波动周期开始的时间)；

t_end = 15; %结束时间(即pH值波动周期结束的时间)；

t=t_start:t_s:t_end;%pH值波动完成一个周期所需的时间；

y=(8.66-0.53*t).*(t≥0&t<4)+(4.0+0.65*t).*(t≥4&t<7)+(8.50).*(t≥7&t<15);%pH值

(y)随时间(t)变化的函数关系式；

yy=fft(y); %对pH值随时间变化的函数关系作傅里叶变换；

subplot(2,1,1); %指出即将作出原始信号图(即pH值(y)随时间(t)变化的函数关系图)的位置；

plot(t,y);title('original signal'); %作原始信号图,即pH(y)随时间(t)变化的图；

Druation = t_end -t_start; %计算采样时间；

Sampling_points=Druation/t_s+1; %采样点数；

fs=1/t_s; %采样频率；

fx=0:fs/(Sampling_points -1):fs; %频率分辨率就是fs/(Sampling_points -1)；

F=abs(fftshift(yy)); %取傅里叶变换正值部分(没有必要取负值)；

subplot(2,1,2); %指即将作出的图像的位置(将0频率分量移到坐标中心的图)；

plot(fx-fs/2,F);title('shift fft transform'); %将角频率最大的峰移到坐标中心。

运行上述matlab程序后，即得图1。在图1的原始信号图中，横坐标表示时间，纵坐标表示的是体系的pH值。原始信号图所示的曲线是一条折线，pH值先下降，再上升，然后又平稳。从图1的原始信号图中根本无法查知生长基元的种数。但图1中的频谱图却可快速得出结论：只有一种生长基元起主导作用，因为频谱图中只有一个主峰。频谱图中的横坐标表示频率。但需指出，将角频率最大的峰移至坐标中心，但并不是说此峰的角频率为0,这仅是作坐标变换，目的是使主频峰便于观测与比较而已。如果不将角频率最大的峰移至坐标中心，将不便观察。其实，图1频谱图中的主峰也可认为被位于过0点中心线拆为两个峰，分别位中心线两侧，不过中心线两侧是完全等同的，最终也是只有一个主峰，下文的图2和图4也属于这种情况。这方面涉及傅里叶变换比较抽象的内容，这里不便多作阐述，可参考文献[17]。频谱图有多少个主峰，就有多少种生长基元起作用。因此，频谱图证明了在文献[21]中，金属离子与OH-组成的生长基元只有四面体[M-(OH)4](M表示金属离子镁或铝)这一种。M解离与结合OH-的动态平衡是致使晶须生长体系pH值周期波动的主要原因。这种解离与结合导致体系pH值波动的过程如下：

[M-(OH)4]→M+4OH-pH值升高

M+4OH-→[M-(OH)4] pH 值降低

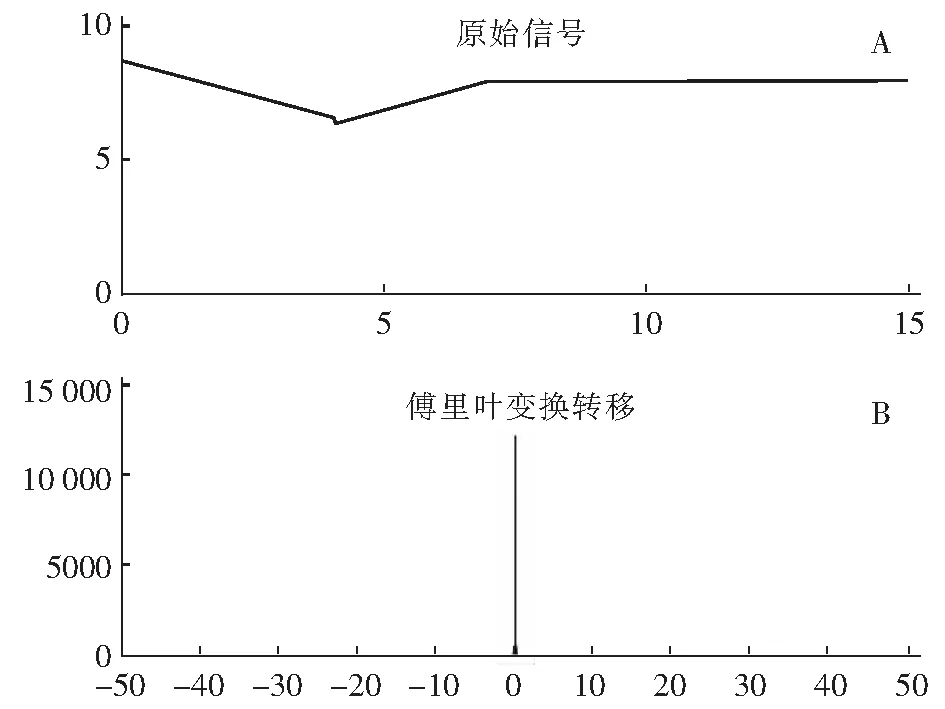
图1 (1)式傅里叶变换图Fig.1 Fourier transform diagram of formula(1)

2.2 文献[22]数据的傅里叶变换

现讨论文献[22]的情况，其pH值y随时间t的变化规律的函数关系为:

(3)

将(3)式写成matlab表达式：y=(8.9-1.1*t.^(2/3)).*(t>=0&t<=9)+(0.63*t.^(6/7)).*(t>9&t<=15),

仿照上文2.1中的matlab代码进行傅里叶变换并作图，可得图2。

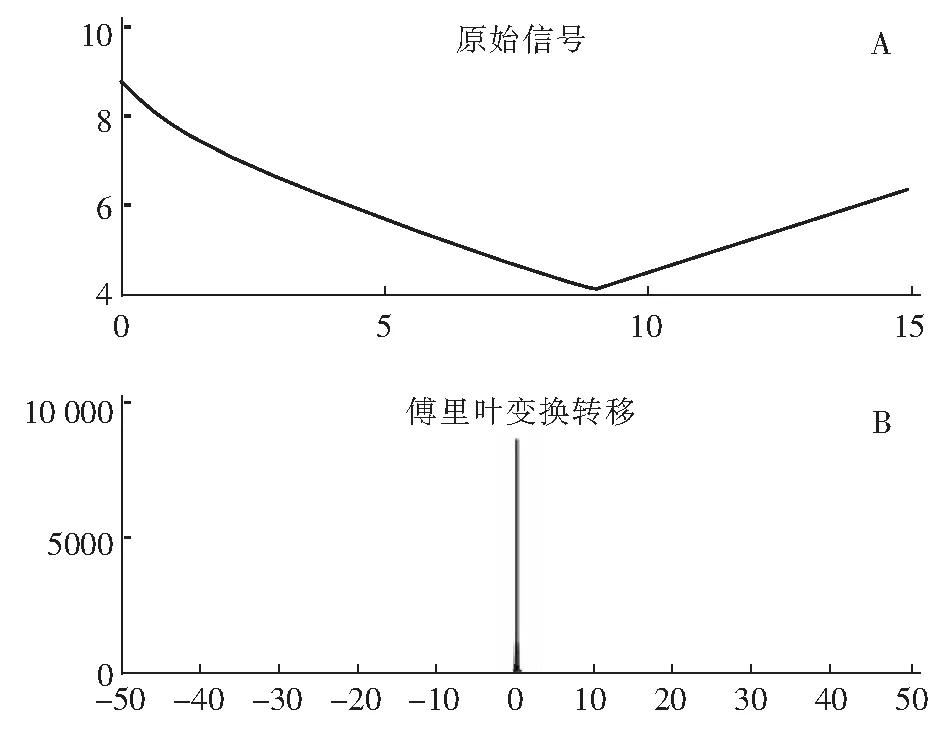
图2 (3)式傅里叶变换图Fig.2 Fourier transform diagram of formula(3)

从图2频谱图可见，频谱图中也只有一个显著的频谱峰，因而证明文献[22]与文献[21]相似，也只有一种生长基元[M-(OH)4]。究其原因，是因为这两篇文献都是在弱碱条件下生长晶须，使得金属离子与OH-只是形成一种四面体结构的生长基元。如果将文献[21]和[22]的pH值都用强碱将其调至pH值=11,增强体系碱性。那么它们在同样的生长条件下产物都只是生成片状晶体而不是晶须。它们的傅里叶变换所得的频谱(为便于讨论，这里只提供了频谱图，其他均忽略)见图3。 图3中虽然出现了4个峰，但实际上只有两个峰，因为“0点”左边谱线和右边谱线是等同的，这是由傅里叶变换规律决定的。图3的A、B分图分别对应文献[21]与[22]。图3之所以出现了两个主峰，究其原因，是因为在较强的碱性条件下，镁离子与OH-形成的是四面体[Mg-(OH)4]，但铝离子与OH-形成的却是八面体的[Al-(OH)6]。因此其傅里叶变换所得频谱上出现了两条显著的谱线，它们分别对应四面体生长基元与八面体生长基元解离与结合OH-的动态平衡，图3中峰高较高的对应[Mg-(OH)4]，较低的对应[Al-(OH)6]。八面体的解离与结合OH-(致使生长体系pH值波动)的动态平衡为：

[M-(OH)6] → M + 6OH-pH值升高

M+6OH-→[M-(OH)6] pH值降低

八面体的这种解离与结合平衡加上四面体的解离与结合平衡，就促成了在碱性较高的条件形成两个主频峰的原因。

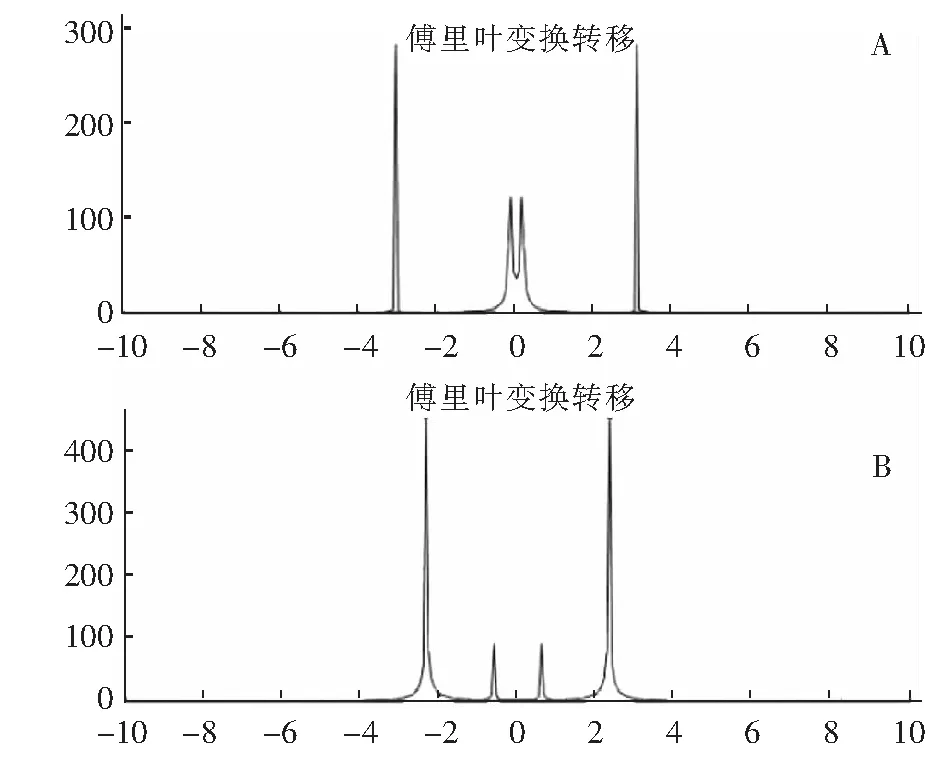
图3 pH值=11时的傅里叶变换频谱图Fig.3 Fourier transform spectrum at pH=11

如果继续将文献[21]与[22]体系的pH值用碱液调至pH值=12.5, 其频谱图见图4，A分图与B分图分别对应文献[21]与[22]。这时发现两频谱图中都只出现一条谱线，证明此时镁与铝都形成了八面体[M-(OH)6]生长基元，因此生长基元又只有一种。生长体系处于这种情况下也是生成片状晶体而不是晶须。

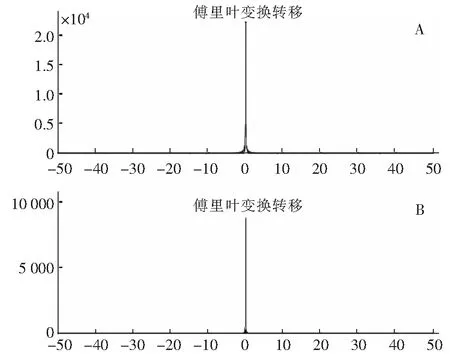
图4 pH值=12.5时的傅里叶变换频谱图Fig.4 Fourier transform spectrum at pH=12.5

2.3 文章提供的傅里叶变换法的准确性及优点的一个简单实验验证

在制备碱式硫酸镁晶须时，可在MgSO4·7H2O中加入少量的碱液，混合后再经水热反应后得到。这里仅是提供在确认晶须生长基元时，傅里叶变换法与拉曼光谱法的对比以凸显傅里叶变换的准确性与优点，其他的制备过程与表征等均不做赘述。

向MgSO4·7H2O溶液中加入少量的NaOH溶液(使pH值=8.8)后，即得碱式硫酸镁晶须生长体系。如果是采用拉曼光谱法去测定[Mg(OH)4]生长基元并确认，那么这个拉曼光谱法是比较费时费力的，甚至测不出来。因为用液相样品测拉曼比较难也比较繁，要做很多参数改变或修正。即使最终测出来，效果也不是很好。图5就是此体系下的拉曼光谱图，图5中标记为“5”的峰正是[Mg(OH)4]的拉曼位移峰，可见此峰比较弱，它远不如标记为1至4的峰强(特别是标记为“3”的峰)。图5中从左至右的4个峰依次是硫酸根的451 cm-1附近的弯曲振动峰、610 cm-1附近的弯曲振动峰、981 cm-1附近的对称伸缩振动峰和1 109 cm-1附近的变形振动峰。可见硫酸根的拉曼位移峰都比[Mg(OH)4]2-强，很易将[Mg(OH)4]2-峰“淹没”。

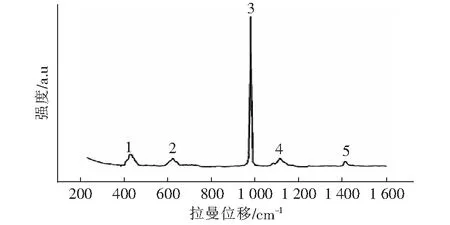
图5 碱式硫酸镁晶须生长体系拉曼位移图谱Fig.5 Raman shift spectra of basic magnesium sulfate whisker growth system

如果按照文章提供的傅里叶变换法方法，得到的傅里叶变换图谱见图6。

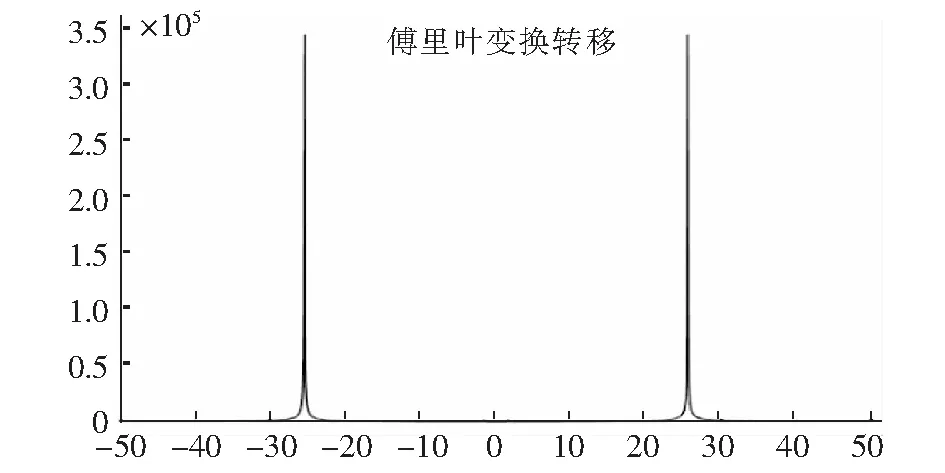
图6 碱式硫酸镁晶须生长体系傅里叶变换图谱Fig.6 Fourier transform spectrum of basic magnesium sulfate whisker growth system

图6表明只有一种生长基元(因为横坐标0的两边分别只有一个主峰(或谱线))，因此判定这一种生长基元即[Mg(OH)4]，一目了然，简单又快捷。从图6也可见，硫酸根的峰不出现在其中，这是因为这种仅以pH值随时间变化的函数的傅里叶变换与硫酸根无任何关系，因此对[Mg(OH)4]基元的测定无任何影响，不像拉曼光谱那样，[Mg(OH)4]峰受到硫酸根峰的严重干扰。

3 结论

傅里叶变换后得到的频谱，可直接读出生长基元的种数。它比采用拉曼光谱法指认生长基元要简化得多，省时省力，为研究晶须生长机制提供了重要的信息。这一变换更直接地反映液相体系下晶须生长基元真实存在的事实。也从数学角度进一步证明了ACP理论和拓展的ACP理论的科学性。将matlab这重要的数学工具应用到晶体、晶须生长研究中来，必然能更直接、更具体、更鲜明地揭示晶体、晶须生长的内在规律。