基于LSTM网络模型的高速公路软基长期沉降预测
2021-07-22郑罗春
郑罗春
(湖南省交通科学研究院有限公司, 湖南 长沙 410015)
0 引言
基于以上讨论,本研究拟将高速公路路基长期沉降变形作为时间序列对待,并基于LSTM神经网络算法构建智能预测模型,进一步结合实际监测数据对所构建模型进行验证。
1 LSTM模型构建及数据集处理
1.1 LSTM模型构建
LSTM网络作为循环神经网络中一分支,其有效的拓扑结构设计可解决一般循环神经网络中易于出现的梯度爆炸或梯度消失等数值问题[11]。对于LSTM模型而言,其基本单元为遗忘门、输入门、输出门、记忆细胞状态以及隐藏单元,如图1所示。LSTM可以较好保存时间序列内部蕴藏的有效信息,并及时剔除无效信息,因而具有长短期记忆能力。
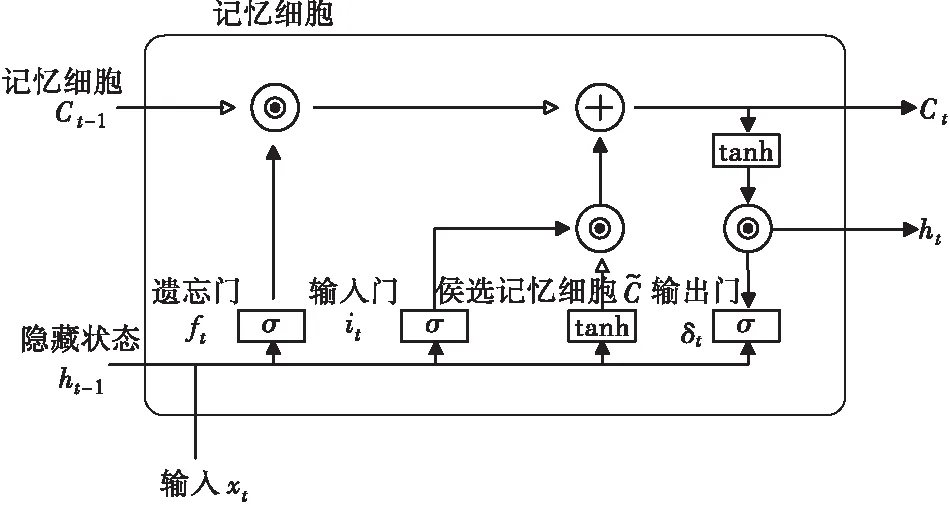
图1 LSTM网络模型结构
在LSTM模型中,其遗忘门可对输入信息进行筛选,并将适用信息保留进细胞状态中,其具体计算方式如式(1)所示:
ft=σ(Wfxt+Rfht-1+bf)
(1)
式中:Wf和Rf为遗忘门权重矩阵;bf为其偏置矩阵;xt则表示当前时刻t的输入值;ht-1则表示上一时刻t-1隐藏状态值;σ则表示Sigmoid函数,其计算方式如下:
(2)
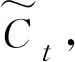
it=σ(Wixt+Riht-1+bi)
兴建小型农田水利工程势必会占用大量土地甚至是农田,在一定程度上影响动植物生长环境,迫使陆生生物重新寻找栖息地,在寻找过程中可能导致动物的死亡,生活在原有栖息地的生物之间为了争夺有限的空间会引发争斗,导致生物链的破坏。工程施工过程中占用的土地,经过工业废料的排放导致土地硬化无法进行耕种减少了耕地面积。
(3)
(4)
式中:Wi、Ri、Wc和Rc分别输入门以及临时细胞状态权重矩阵;bi和bc分别表示输入门以及临时细胞状态偏置矩阵;tanh 函数具体计算方式如下:
(5)
经过上述流程对数据流进行分析后,便可将所获取结果进行叠加,从而实现对细胞状态的更新,计算方式如下式所示:
(6)
数据流经上述处理后,便由输入门进行输出Ot,进一步结合输出门结果以及当前细胞状态,则可获得当前时刻隐藏状态信息ht,以便进行下一个循环计算,其具体计算方式如下:
Ot=σ(Wyxt+Ryht-1+by)
(7)
ht=Ottanh(Ct)
(8)
式中:Wy和Ry为输出门权重矩阵;by为其偏置矩阵。
1.2 数据集获取及预处理
本研究拟采用文献[13]中针对某高速公路监测过程中所获取的实测数据作为数据样本对所提出模型预测性能进行验证,如图2所示。为更全面论证所构建模型的正确性,本研究分别选取K38+210以及K32+100两个断面作为模型验证样本数据。考虑到本研究侧重于高速公路路基长期沉降问题,因而对实测数据进行剔除处理,选定沉降速率极值点后数据集进行预测。
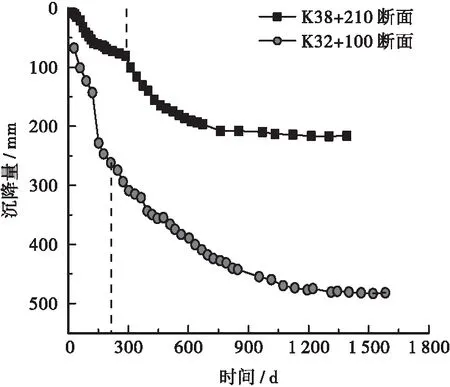
图2 数据集曲线
对于LSTM模型而言,为充分使得模型内部元件具有样本记忆功能,应当利用已有数据集对其进行训练。在本研究中,拟将所采集数据集前段80%作为训练集数据值所构建LSTM模型进行训练。当训练完成后,利用LSTM模型多步预测功能对后续沉降值进行预测。除此之外,对于神经网络模型而言,其输入及输出样本数据集数值浮动将对最终训练结果及预测结果产生显著影响,因而在对其进行模型训练时,应当对其输入及输出数据集进行归一化处理,在本研究中,拟采用对样本数据进行归一化,具体计算方式如下:
(9)
式中:x表示原始样本数据数值;xmax和xmin分别表示样本数据集中最大值及最小值。经由上述归一化处理后,模型训练集数据数值均被归一化至0-1范围内。
2 模型预测及精度评估
2.1 模型预测结果对比分析
为进一步准确验证本研究所提出LSTM模型的预测能力,在采用LSTM模型对高速公路地基长期沉降进行预测的同时,继而采用文献[14]所给出的指数曲线法对所采集沉降数据进行预测,指数曲线法基本表达式如下式所示:
s(t)=s∞-(s∞-s0)e(t0-t)/η
(10)
式中:s∞表示最终观测沉降量值;t0表示任意观测时刻;s0则表示时刻所对应的观测沉降值;η为模型拟合参数。
通过分别采用LSTM模型和指数曲线法进行预测,得到实际观测结果与预测结果对比曲线如图3所示。从图中可知,采用本研究所提出的LSTM模型获取的预测结果与实测结果较为接近,充分论证了本研究所提出高速公路长期沉降预测模型的正确性和合理性。
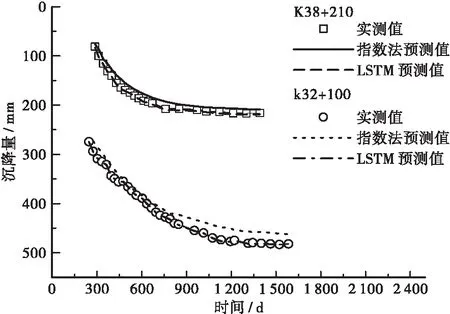
图3 不同预测方法结果对比
2.2 精度评价
为对模型预测精度进行评价,本研究中分别采用绝对误差(erri)和相对误差(r_erri)对不同数据点精度进行表征。其计算公式分别如下:
(11)
式中:pi和oi分别表示第i个数据点的预测值和实测值。
通过计算得到不同数据点相对误差值以及绝对误差值如图4所示。从图中可知,采用LSTM模型进行预测时,对于K38+210以及K32+100两断面而言,其平均绝对误差分别为0.65 mm和0.27 mm,平均相对误差值分别为1.23%和0.15%。就采用指数曲线法所获取的预测结果而言,对于K38+210以及K32+100两断面,其平均绝对误差分别为-4.96 mm和-9.21 mm,平均相对误差值分别6.92%和2.67%。上述结果表明,本研究所提出的LSTM模型可有效反映高速公路地基长期沉降特征,相较于传统的指数曲线法而言,LSTM模型预测精度较高。
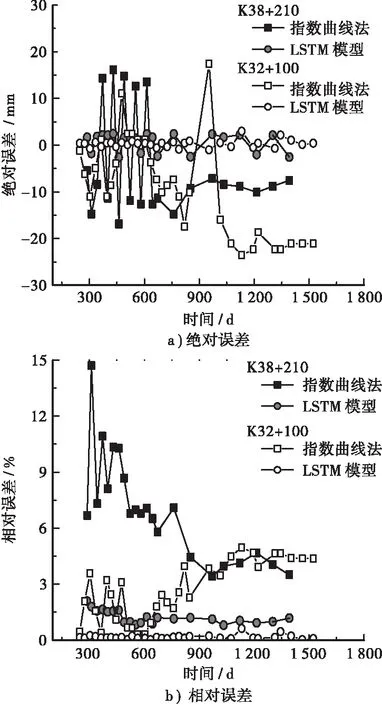
图4 不同预测方法误差对比
上文采用误差分析指标对LSTM模型预测能力进行了初步评估,为更为直观地表征两类预测方法的预测能力,进一步利用其预测值和实测值进行回归分析,得到如图5所示结果。从图中可直观看出,LTSM模型预测值与实测值高度接近,对于K38+210以及K32+100两断面而言,其R值分别为0.996和0.998,而采用指数曲线法进行预测时,两断面R值分别为0.912和0.901。由此进一步表明,本研究所提出LSTM模型在预测高速公路地基长期沉降问题上具有显著的高精度优势。
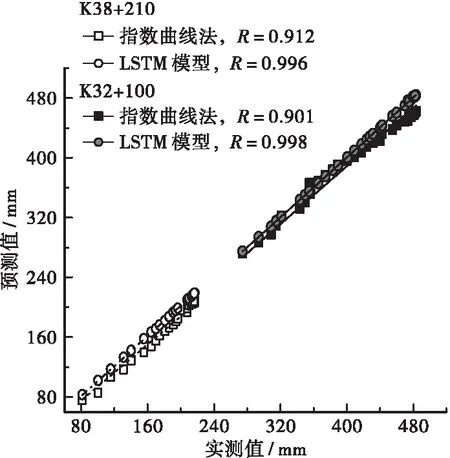
图5 不同预测方法回归分析
3 结论
考虑到高速公路建设和运行过程中,路基长期沉降将对其使用性能产生巨大影响,进一步认识并实现对路基长期沉降行为的预测可为实际工程运行和维护提供有效参考。本研究针对高速公路路基沉降问题展开研究,得到如下主要结论:
1) LSTM神经网络模型相较于一般曲线拟合方法具有容错性好、记忆功能强等显著优势,可有效识别并保存已有数据中的隐藏信息特征。基于以上优势,本研究构建得到了针对高速公路路基长期沉降预测的LSTM神经网络模型。
2) 在本研究中,利用高速公路路基长期沉降特征的时序化特征,基于LSTM神经网络模型对其进行预测,结果表明,所构建LSTM模型可有效表征高速公路路基长期沉降的非线性特征,相比较于指数曲线法而言,其误差低、预测精度较高。
3) 考虑到实际工程建设中,高速公路的使用年限较长,构建合理预测高速公路路基沉降预测模型,可有效利用现有检测数据实现对其长期变形行为的高精度预测,可为高速公路的维护提供有效参考,具有较高的实际工程价值。
