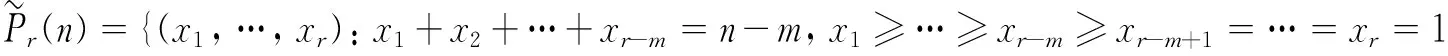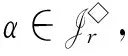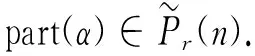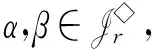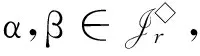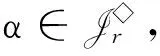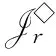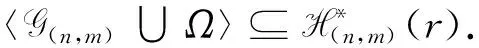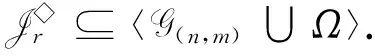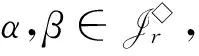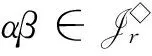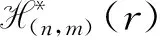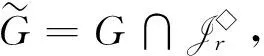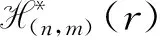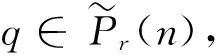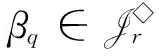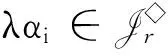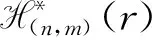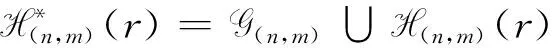半群的秩

袁 月，赵 平

贵州师范大学 数学科学学院，贵阳 550001

设n，m∈N+，Sn和Tn分别是Xn={1，2，…，n}上的对称群和全变换半群.对于1≤m≤n-1，记Xm={1，2，…，m}.令

T(n，m)={α∈Tn：Xmα=Xm}

G(n，m)={α∈T(n，m)：(XnXm)α=XnXm}

H(n，m)={α∈T(n，m)：(XnXm)α⊆XnXm}

则易证得G(n，m)，H(n，m)和T(n，m)都是全变换半群Tn的子半群，且G(n，m)⊆H(n，m)⊆T(n，m).显然G(n，m)=T(n，m)∩Sn且G(n，m)≅Sm×Sn-m，其中Sn-m是XnXm上的对称群.

对于r∈N+且2≤m+1≤r≤n-1，记

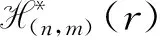
通常，我们定义有限半群S的秩为

rankS=min{|A|：A⊆S，〈A〉=S}

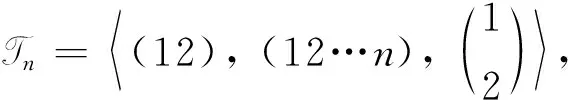
S(n，1)=S(n，n)=1S(n，r)=S(n-1，r-1)+rS(n-1，r)

文献[5]研究了半群Tn，r=Sn∪T(n，r)的生成元和相关秩.文献[6]研究了G(n，m)的生成集及秩，并得到T(n，m)的秩，即

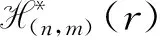
为了叙述上的方便，在H(n，m)上引入以下的二元关系：对任意α，β∈H(n，m)，定义

αL◇β⟺im(α)=im(β)

αR◇β⟺ker(α)=ker(β)

αJ◇β⟺|im(α)|=|im(β)|

则L◇，R◇与J◇都是H(n，m)上的等价关系.易得L◇⊆J◇，R◇⊆J◇.对r∈N+且2≤m+1≤r≤n，记

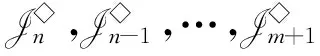
设1≤m≤n-1，用Sn-m，Tn-m分别表示XnXm上的对称群和全变换半群.用Sm表示Xm上的对称群.设α∈Tn，记ker(α)={(x，y)∈Xn×Xn：xα=yα}，则ker(α)是Xn上的等价关系，称为α的核.

引理1[6]设1≤m≤n-1，则

对于2≤m+1≤r≤n，记

H(n，m)(r)={α∈H(n，m)：|im(α)|≤r}

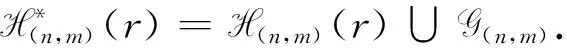
H(n，m)(m+1)⊆H(n，m)(m+2)⊆…⊆H(n，m)(n)=H(n，m)

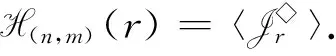
任意取n，r∈N+且r

Pr(n)={(x1，…，xr)：x1+x2+…+xr=n，x1≥x2≥…≥xr≥1且x1，…，xr∈N+}

称集合Pr(n)中的元素(x1，x2，…，xr)为n的一个r-划分，记pr(n)=|Pr(n)|(参见文献[16]).当xr-m+1=xr-m+2=…=xr=1(1≤m

则

其中Ai={i}(1≤i≤m)，Xm={a1，a2，…，am}且ai∈XnXm(m+1≤i≤r).显然存在σ∈Sr，使得|Arσ|≥|A(r-1)σ|≥…≥|A(m+1)σ|≥1且Aiσ=Ai(1≤i≤m).记

part(α)=(|Arσ|，|A(r-1)σ|，…，|A(m+1)σ|，|Amσ|，|A(m-1)σ|，…，|A1σ|)

βi=λiδiμi∈〈G(n，m)，δi〉

从而

因此

证设α，β的标准形式为

因此ker(αβ)=ker(α).

证由引理2可得

则

βq=α1…αi-1αiαi+1…αt=(1Xnα1…αi-1)αi(αi+1…αt1Xn)

定理1设2≤m

|G∩H(n，m)(r)|≥pr-m(n-m)

|G|≥pr-m(n-m)+2

从而

由rank G(n，m)=2可知，存在λ，μ∈G(n，m)，使得G(n，m)=〈λ，μ〉，于是由引理4可得

从而

因此