基于LCD-RQA的滚动轴承故障诊断与健康评估
2021-07-21周博王瑶瑶刘双燕文振华
周博,王瑶瑶,刘双燕,文振华
(郑州航空工业管理学院 a.民航学院;b.航空工程学院,郑州 450046)
滚动轴承的工作状况对旋转设备的运转起着至关重要的作用[1],相关调查研究发现,滚动轴承引起的问题占旋转设备故障的40%以上,因此,对滚动轴承进行故障诊断与健康评估的研究具有重要意义[2],其关键是对传感器所获取信号进行处理并提取有效的故障特征。实际工作中,由于机械部件的负载、摩擦力、阻尼不断变化,导致产生的振动信号常呈现出明显的非线性非稳态特点[3]。传统基于傅里叶变换的方法只能处理线性和平稳信号,因此对非平稳信号的特征提取成为机械故障诊断领域的重要课题[4]。
国内外研究人员针对非稳态信号的故障特征提取做了许多研究,傅里叶变换、Wigner-Ville分布、小波变换、希尔伯特-黄变换(HHT)、局部均值分解(LMD)等时频分析方法可以同时得到振动信号的时域信息和频域信息,近年来在旋转机械的故障诊断中应用广泛,且诊断效果良好。然而,上述分析方法在使用中均存在一定的不足:短时傅里叶变换的时频窗口是固定的[5];小波变换母小波的选择和分解层数不具备自适应性[6];HHT实现了信号的自适应分解,但存在过包络、欠包络以及拟合精度差等问题[7];LMD虽然能够改善上述缺陷[8],但其得到的分量往往掺杂着虚假频率,处理过程中还可能会发生信号突变,而且该方法计算量大,运算速度慢。局部特征尺度分解(Local Characteristic-Scale Decomposition,LCD)具有较强的自适应性,能够将非平稳信号分解成为多个内禀尺度分量(Intrinsic Scale Component,ISC)之和[9],相对于前述时频分析方法,LCD对信号的处理速度有很大提升,同时避免了过包络和欠包络的问题,而且降低了拟合误差。
另外,在滚动轴承故障诊断和健康评估的过程中,提取有效的故障特征非常关键,同时也是信号分解的重要内容。递归图是基于相空间重构理论分析时间序列的周期性、混沌性以及非平稳性的重要方法,可以获得信息量、相似性以及预测性等相关内容,了解时间序列的内在构成[10-12]。然而递归图只是一种定性分析方法,无定量判断依据,主要依靠科研人员的经验进行结果判定,客观性不足。因此,尝试通过提取递归图中的一些定量特性对非线性时间序列进行分析[13-14],通过递归定量分析(Recurrence Quantification Analysis,RQA)对滚动轴承进行更准确的故障诊断与健康评估[15]。
综上,将LCD和RQA进行融合,提出了基于LCD-RQA的滚动轴承故障诊断与健康评估方法:首先,利用LCD对传感器获取的滚动轴承振动信号进行自适应分解;然后,对分解的每条曲线进行相空间重构并绘制成为递归图,提取递归图中的递归率、确定性和层流性等作为故障特征;最后,利用提取出来的递归定量特征进行滚动轴承的故障诊断与健康评估。
1 局部特征尺度分解
局部特征尺度分解适用于处理非线性和非稳态信号,该过程将得到n个从高频到低频的内禀尺度分量[16],ISC分量必须满足以下条件:
①在整个数据集上,任何相邻2个极值点的符号互不相同。
②在整个数据集上,对于局部最大(最小)值点(tk,xk),任意临近的最大(最小)值(tk-1,xk-1)与(tk+1,xk+1)由一条直线相连,该直线可表示为
(1)
为保证ISC曲线的光滑性和对称性,xk与Ak的比值为一个常数,即
Ak/xk=(a-1)/a;a∈(0,1)。
(2)
通常情况下,a取0.5,因此Ak=-xk,此时xk与Ak关于x轴对称。
对于一个复杂的信号x(t)(t>0),可按如下步骤进行分解得到ISC分量:
1)选取信号x(t)的极值点(tk,xk)。
2)利用(1)式计算Ak并计算对应的Lk,即
Lk=aAk+(1-a)xk;k=2,…,M-1,
(3)
由于k的取值范围为从[2,M-1],因此需要将数据边界进行延长,设A1(t0,x0)和AM(tM+1,xM+1)为延伸之后两端的极值点,得到L1和LM。
3)将所有的Lk(k=1,…,M)用三次样条曲线L(t)连接,该曲线即LCD的基线。设原始信号与基线之间的差值h1(t)为
h1(t)=x(t)-L1(t),
(4)
若h1(t)满足条件①和②,则h1(t)作为第1个ISC分量;否则将h1(t)视为原始信号重复以上步骤,得
h11(t)=h1(t)-L11(t),
(5)
若h11(t)依旧不满足条件①和②,重复以上步骤k次,直到h1k(t)满足条件成为第1个ISC分量。
4)将第1个ISC分量c1(t)从原始数据x(t)中分离出来,残差记作r1(t),即
x(t)-c1(t)=r1(t)。
(6)
5)继续将残差r1(t)作为原始信号进行处理,重复以上步骤直到最终的残差rn(t)为常数或单调函数,以及极值点不超过3个的函数。则原始信号x(t)被分解成为多个ISC分量与残差之和,即
(7)
式中:ci(t)为第i个ISC分量。
2 递归定量分析
2.1 递归图的生成
递归图的构造原理如下[18]:
1)对于时间序列uk(k=1,2,…,N),其采样间隔为Δt,假设嵌入维数为m,延迟时间为τ,通过文献[19]和互信息法选取恰当的m和τ,得到一个新的时间序列,重构之后的相空间为
xi=(ui,ui+τ,…,ui+(m-1)τ);i=1,2,…,N-(m-1)τ。
(8)
2)计算重构后相空间中的点xi与点xj之间的距离,即
(9)
3)计算递归值。
R(i,j)=H(εi-Sij),
(10)
(11)
式中:εi为截止距离;H(r)为Heaviside单位函数。
4)以i为横坐标,j为纵坐标绘制递归图R(i,j),i,j分别为时间序列标号。
2.1.1 文献[19]方法
文献[19]在进行信号处理时可以清晰地将真实信号和噪声分辨出来,且计算效率较高。
在不同嵌入维数条件下,相空间中各点的最邻近点的距离变化值为
(12)
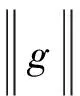
定义2个判别准则,即
(13)
(14)
当时间序列固定不变时存在嵌入维数,若d>d0时,E1(d)和E2(d)停止变化或者波动较小,则最小嵌入维数为d0。
2.1.2 互信息法
互信息函数方法在相空间重构中运用较多,用于估计重构相空间的延迟时间[20]。
对于离散变量X,Y,其联合熵为
(15)
式中:pij为变量X在状态i且变量Y在状态j时出现的概率;m,n分别为X,Y的状态数。
互信息可以定义为
I(X,Y)=H(X)+H(Y)-H(X,Y)。
(16)
设混沌时间序列s1,s2,…,时间延迟为d,嵌入维数为τ,重构相空间得
X(t)={x0(t),x1(t),…,xn(t)},
(17)
xn(t)=s(t+nτ),
(18)
则系统对变量s的平均信息量为系统的熵H,即
(19)
记[s,q]=[x(t),x(t+τ)],考虑一个总的耦合系统(S,Q),假定s已知为si,则q的不定性为
(20)
式中:Pq|s(qj|si)为条件概率。
设在时刻t时x已知,则在x+τ时刻,x的平均不定性为
H(S,Q)-H(S),
(21)
(22)
式中:H(S,Q)为孤立的q的不定性;H(Q|S)为已知s的q的不定性。所以s的已知减小q的不定性,互信息为
I(Q,S)=H(Q)-H(Q|S)=H(Q)+
H(S)-H(S,Q)=I(S,Q)。
(23)
互信息是联合概率分布Psq的函数。从概率分布的直方图中估计Psq通常采用以下方法:设在平面上点(s,q)处有一个大小为ΔsΔq的盒子,那么有
(24)
式中:Nsq,Ntotal分别为盒子中的点数和总点数。
对于一般情况,互信息为
(25)
若In(τ)是一个延迟时间重构,相空间重构的时间延迟则为In(τ)初次达到最小值时的时滞。
2.2 递归定量特征的提取
定义递归图中线结构和点密度中的特征递归率、确定性和层流性等参数来定量地描述时间序列的动态特性[3,13]。
对于相空间重构后的N个向量,根据(10)式构建递归图后,递归率RRR的定义为
(26)
设P(l),P(v)分别为递归图中45°方向和垂直方向直线的长度分布,分别定义为
(27)
(28)
式中:Nl为长度l的45°方向直线的数量;Nv为长度v的垂直方向直线的数量;Nα为长度α的45°方向或垂直方向直线的数量;lmin,lmax为45°方向直线的最小长度(一般取2)和最大长度;vmin,vmax为垂直方向直线的最小长度(一般取2)和最大长度。
确定性RDET和层流性RLAM的定义为
(29)
(30)
递归率、确定性和层流性分别反映了某个特定状态出现的概率以及系统的可预测性、间歇性和层次性,这些递归图中提取的参数都是系统动力学特征的反映,可以作为特征参数用于滚动轴承的故障诊断与健康评估。
3 基于LCD-RQA的滚动轴承故障诊断与健康评估
3.1 算法流程
综合上述理论分析,提出的基于LCD-RQA的滚动轴承故障诊断与健康评估方法的流程如图1所示。

图1 基于LCD-RQA的滚动轴承故障诊断与健康评估流程
3.2 数据准备
以美国Case Western大学所公开的滚动轴承故障诊断试验数据[21]为例进行方法验证。
故障诊断案例以驱动端SKF 6205-2RS型深沟球轴承为研究对象,分别选取1 797 r/min下正常状态以及故障直径为0.534 mm的内圈故障、钢球故障和外圈故障轴承所采集的数据,具体数据组成见表1,利用该数据验证LCD-RQA滚动轴承故障诊断方法的可行性。

表1 试验数据描述
健康评估的案例同样来自驱动端轴承SKF 6205-2RS型深沟球轴承,分别选取1 797 r/min下正常状态、内圈滚道上故障直径分别为0.178,0.356,0.534 mm的试验数据,具体数据组成见表1,利用该数据集验证LCD-RQA滚动轴承健康评估方法的可行性。
3.3 基于LCD-RQA的滚动轴承故障诊断
首先利用文献[19]算法和互信息法计算相空间重构的嵌入维数m和延迟时间τ,计算最小嵌入维数时,以E(d+1)-E(d)<0.01和E*(d+1)-E*(d)<0.01作为(13)式和(14)式的定量判定标准,具体结果见表2。然后利用LCD对4种故障状态的轴承振动数据进行自适应分解,分解层数为5,分解后的各ISC分量如图2所示。
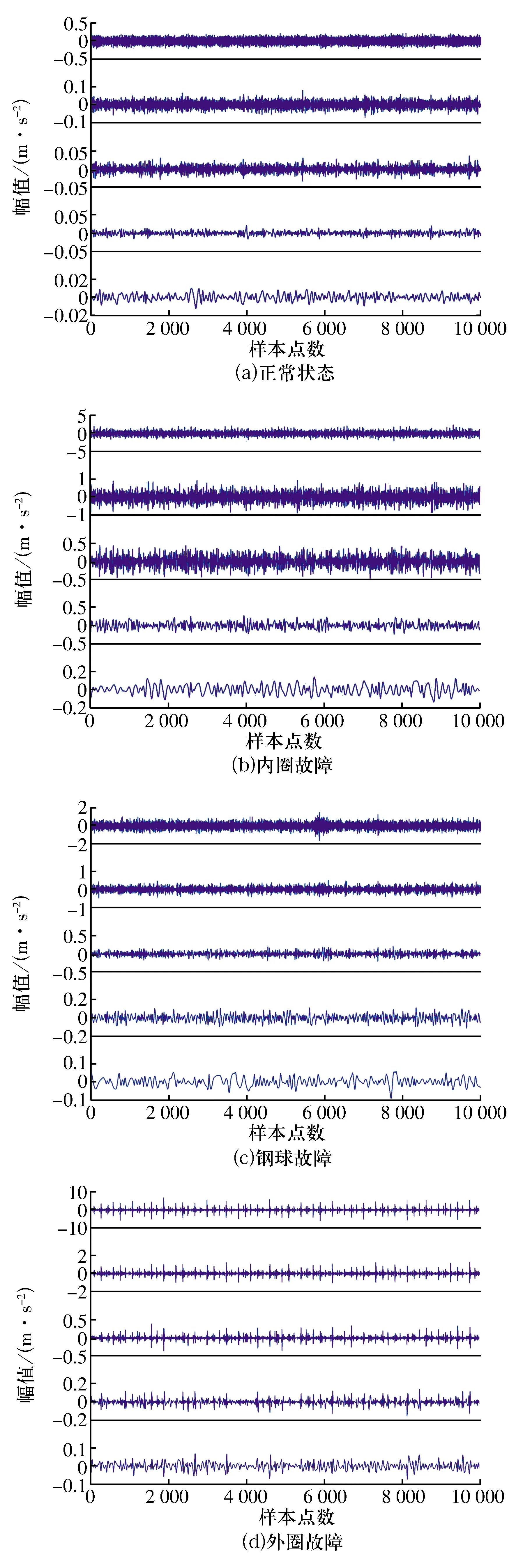
图2 不同故障状态轴承振动数据的LCD处理结果

表2 不同故障状态轴承数据相空间重构参数
将获得的ISC分量转化成为递归图,转化时每次选取的ISC分量长度为1 000个数据点,且每次向后滑移100个数据点来形成多个递归图。不同故障状态轴承振动数据各ISC分量第1~1 000个数据点所转化的递归图如图3所示,由图可知,不同故障状态轴承振动数据的递归图表现出递归点的密度和水平垂直线的结构均不相同。

图3 不同故障状态轴承振动数据的递归图
为定量描述各故障状态轴承振动数据的递归图,分别计算各递归图的递归率、确定性和层流性并将计算结果绘制在三维散点图中,结果如图4所示,由图可知:轴承振动数据的递归特征具有很好的可分性,同一故障状态的递归定量特征具有很好的聚集性,说明本方法可以很好地对滚动轴承进行故障诊断。
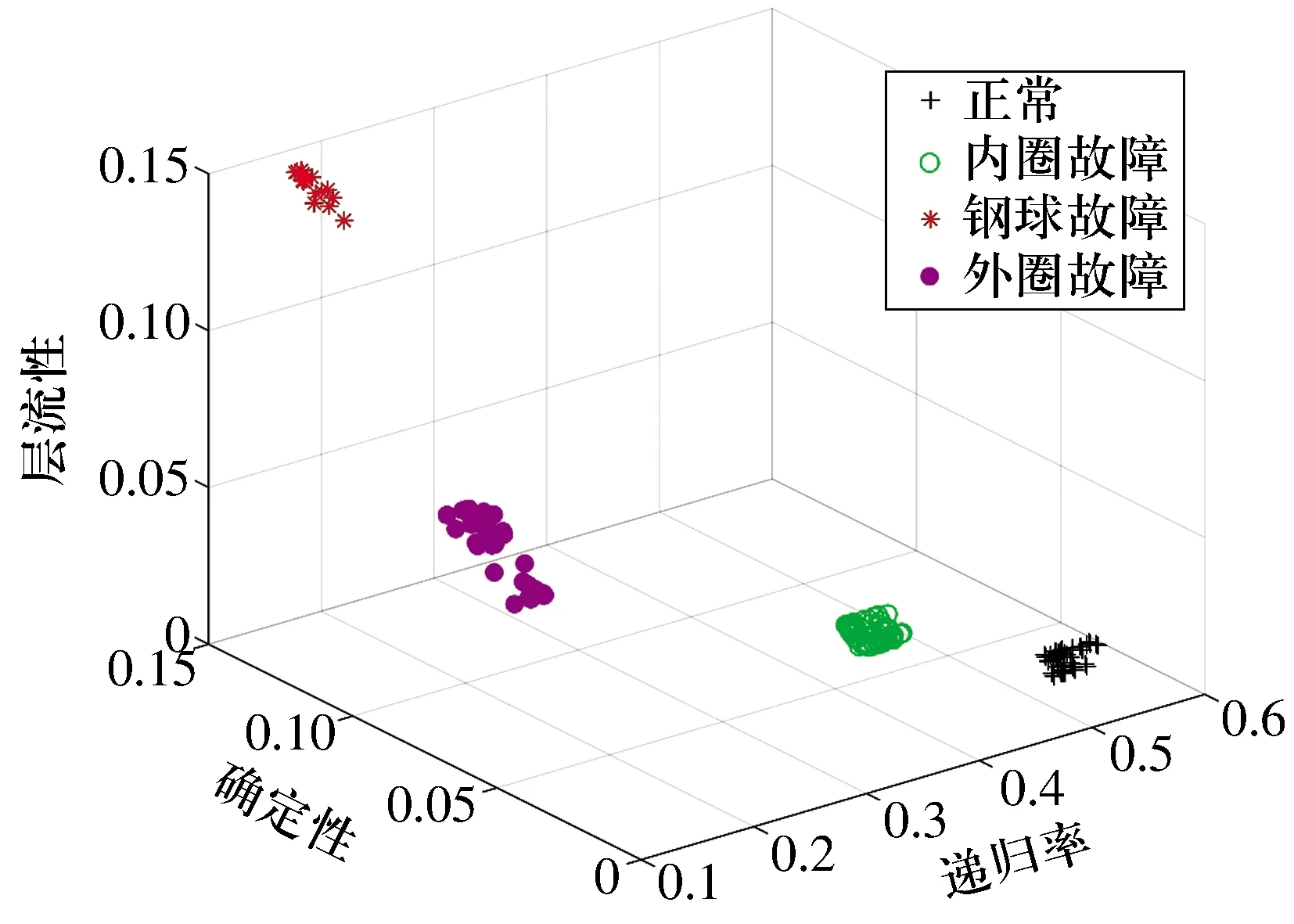
图4 不同故障状态轴承振动数据递归特征的三维散点图
3.4 基于LCD-RQA的滚动轴承健康评估
同样,利用文献[19]算法和互信息法计算相空间重构的嵌入维数m和延迟时间τ,计算最小嵌入维数时,以E(d+1)-E(d)<0.01和E*(d+1)-E*(d)<0.01作为(13)式和(14)式的定量判定标准,具体结果见表3。然后利用LCD对正常状态及不同内圈故障程度的轴承进行自适应分解,分解层数为5时所得各ISC分量如图5所示。

表3 不同故障程度轴承振动数据的相空间重构参数

图5 不同内圈故障程度轴承振动数据的LCD处理结果
将获得的ISC分量转化成为递归图,转化时每次选取的ISC分量长度为1 000个数据点,且每次向后滑移100个数据点来形成多个递归图。不同内圈故障程度轴承振动数据各ISC分量第1~1 000个数据点所转化的递归图如图6所示,由图可知递归点的密度和水平垂直线的结构随着轴承故障程度的增加而改变[3]。

图6 不同内圈故障程度轴承振动数据的递归图
正常状态循环计算300组,3种程度内圈故障数据均循环计算200组,生成递归率、确定性和层流性这3类递归定量分析特征参数。将正常状态的前100组特征作为健康评估的标准数据,其余数据的故障特征作为测试数据,计算测试数据递归定量特征与正常数据递归定量特征之间的欧式距离,并将所计算的欧式距离转化成为置信度(CV)以表示滚动轴承的健康程度,即
(31)
式中:di为欧式距离;a为计算标准化参数。
正常数据与测试数据之间的欧式距离及CV值如图7所示,由图可知:测试数据正常样本与标准数据之间的欧式距离非常小,在0附近波动,随着故障程度的加深,各故障样本与标准数据之间的欧式距离逐渐增大;将欧式距离曲线转换成为CV值并归一化到[0,1],正常情况的CV值在1附近,随着故障程度的加深,该滚动轴承的健康度在不断下降。

图7 不同故障程度轴承振动数据的欧式距离和健康度
根据经验将正常阈值设定为0.8,完全故障的阈值设定为0.4,根据故障注入的要求,故障程度1的滚动轴承故障程度较轻,该状态下的健康度可接受,轴承可继续使用;故障程度2的滚动轴承健康状态已经接近完全故障,而故障程度3的滚动轴承健康状态低于设定的完全故障阈值,判断为不可使用。可根据该参数设定下的模型对后续设备进行健康评估。
4 结束语
针对滚动轴承振动信号非线性非平稳的特点,提出了一种基于局部特征尺度分解及递归定量分析的滚动轴承故障诊断和健康评估方法。通过局部特征尺度分解对滚动轴承振动信号进行分解,将分解后的各ISC分量转化为递归图并计算其定量特征。试验数据的三维散点图可看出各故障状态具有很好的可分性,健康评估中测试数据与标准数据的欧式距离及置信度则表明随着故障程度的加深,滚动轴承健康度在逐渐下降。该方法对非线性振动信号具有良好的适用性,对滚动轴承的故障诊断和健康评估应用效果显著。
