云巴线路平面曲线参数研究
2021-07-21王楚骄
王楚骄,陈 剑
(中国铁路设计集团有限公司,广东深圳 518000)
1 引言
根据中国城市轨道交通协会发布的《比亚迪城轨交通系统的调研考察报告》,比亚迪云巴系统运量为0.6~1万人次/h,属于小运量胶轮有轨电车系统,是现代有轨电车的一种新系统,适用于三四线城市的骨干线和一、二线城市的辅助线、加密线、区域循环线。目前全国范围内已有重庆、深圳、天津、西安等地在建或规划建设云巴线路。
云巴的研究尚处于初步阶段,目前所形成的规范文件均缺少对条文(特别是线路技术参数条文)的详细解释。云巴与钢轮钢轨制式、跨坐式单轨制式、公交系统均有相似之处,但又存在较大差异。本文在参考其他轨道交通成熟计算理论的基础上,结合云巴的特点对线路曲线参数进行研究,有助于深化设计者对规范条文中线路技术参数的理解及促进本制式系统推广。
2 云巴系统简介
云巴是由比亚迪自主研发的一款小运量轨道交通系统,轮轨系统采用橡胶轮胎内嵌于U型梁的结构模式,动力系统为车载蓄电池组供电,电池为磷酸铁锂电池,道岔采用SAS型道岔,信号系统采用无人驾驶,车站设计采用无人值守,区间疏散方式采用端门疏散。因其结构体量轻盈、振动噪声对环境影响小,故一般情况采用高架敷设方式,如图1所示。根据广东省住房和城乡建设厅颁布的DBJ/T 15-172-2019《胶轮有轨电车交通系统设计规范》(以下简称《广东省标准》),相关参数如表1所示。

表1 云巴车辆主要技术参数表

图1 云巴系统
3 云巴舒适度标准
关于舒适度评价,不同国家有不同的标准,国内不同文献、规范所采用的标准也不尽相同,其评价指标主要有未被平衡的离心加速度a、滚动角时变率f、未被平衡的离心加速度时变率b、离心加速度变化率ap等。不同规范采用的的舒适度指标如表2所示。

表2 不同规范舒适度标准
从表2中可以看出,除未被平衡的离心加速度外,钢轮钢轨制式的铁路系统主要以未被平衡的离心加速度时变率b及滚动角时变率f作为舒适度标准来考虑;公路系统参照铁路的舒适度标准并结合道路设计的特点采用离心加速度变化率ap作为主要的舒适度考虑指标;跨坐式单轨则采用与公路系统相同的指标,但标准相对提高。目前云巴系统的舒适度标准尚未有正式的文献作出详细分析。《广东省标准》第6.2.6条的条文说明中提出滚动角时变率取f= 0.027 9 rad/s、离心加速度时变率取b= 0.35 m/s3。按允许最大欠超高率为5%,对应允许未被平衡的离心加速度ap= 0.5 m/s2。
综上分析,在编制《广东省标准》的过程中,关于舒适度评价,编制者同时考虑了滚动角时变率与离心加速度时变率2项指标,然而这2项指标一般不同时出现在同一系统中。规范编制者作此考虑的原因可能是云巴系统兼具公路系统与铁路系统的特点,故未将其清晰界定。结合笔者在深圳坪山云巴1号线的设计经验,因在设计过程中均采用铁路的设计思维及方法,建议云巴的舒适度指标与TB 10098-2017《铁路线路设计规范》采用相同的指标,以便于系统制式的推广。
4 平面参数研究
4.1 最小曲线半径
曲线半径的选定与线路性质、车辆性能、行车速度、地形地物等条件有关,其选定是否合理会直接对城市轨道交通的工程造价、运行速度、乘客舒适度及运营成本等产生很大影响。从提高旅客舒适度、减少轮胎磨耗、提高线型标准的角度来讲,平面曲线半径宜尽可能选取较大值。本文将从以下2个方面对最小圆曲线半径的取值进行分析。
4.1.1 满足车辆构造条件下的最小曲线半径
云巴转向架为单轴转向架,其结构如图2所示。云巴车辆在圆曲线上的运行状态如图3所示,当θ角达到转向架的最大转角时,所对应的转弯状态即为极限状态,此时的圆曲线半径R即为最小转弯半径。根据图3几何关系可知:

图2 云巴车辆转向架示意图

图3 云巴车辆在圆曲线上的几何关系示意图

式(1)中,Rmin为最小转弯半径,m;L为车辆轴距,m;θ为转向架最大转角,°。
云巴车辆的转向架最大转角θ为8°,车辆中心轴距L为4.2 m ,代入式(1)中可得Rmin≈15 m。
4.1.2 基于目标旅行速度条件下的曲线半径
《广东省标准》第6.2.2条规定“正线平面最小曲线半径一般情况下不宜小于30 m”,但缺少条文解释,没有对“一般情况”进行说明。根据GB 50157-2013《地铁设计规范》,“一般情况”考虑的因素主要有运营条件、轮轨磨耗等,但未对运营条件有详细的说明和数字支撑。
衡量城市轨道交通运行效率的主要指标为旅行速度,GB 50157-2013《地铁设计规范》及建标 104-2008《城市轨道交通工程项目建设标准》均对旅行速度作出了要求。建立基于目标旅行速度与区间下限速度之间的关系,进而通过速度与曲线半径之间的关系明确旅行速度对最小曲线半径选取的要求,是一种较为可行的研究思路。城市轨道交通中全线旅行速度的计算如式(2)所示:

式(2)中,Li为第i个区间的站间距;Ti为第i个区间的运行时间;ti为第i个站的停站时间;n为车站总数。
根据式(2)可知,旅行速度与站间距、区间限速及停站时间密切相关,线路的平均站间距越大旅行速度越高,区间限速值(含上、下限)越高旅行速度越高,停站时间越长旅行速度越低。只有在保证绝大部分区段满足旅行速度要求时,才能保证全线旅行速度达到要求,也即一般情况下区间的旅行速度不宜低于规范规定的旅行速度值V规定:

式(3)中,V旅j为第j个区间的旅行速度;Lj为第j个区间的站间距;Tj为第j个区间的运行时间;tj为第j个车站的停站时间;V规定为规范中对旅行速度的规定值。根据《广东省标准》3.1.2条“列车旅行速度不宜低于25 km/h”,故取V规定= 25 km/h。
根据《广东省标准》3.3.3条“车站设计最小停站时间一般站为25 s”,因此本文采用停站时间tj= 25 s。不同的站间距在其他限制条件一致的情况下所得出的旅行速度不一致,因平均站间距具有较强的代表性,故Lj采用平均站间距。云巴一般作为一、二线城市的加密线、区域循环线及三、四线城市的骨干线,线路的平均站间距介于城市公交系统与大运量轨道交通系统之间,如表3所示,一般在600~1 000 m左右,按最不利情况考虑,采用Lj= 600 m。

表3 部分云巴线路概况一览
根据《广东省标准》表4.1.2“云巴的最高运行速度为80 km/h,常用加/减速度均为1 m/s2”,在600 m站间距条件下的速度-时间曲线如图4所示。

图4 600 m站间距下列车运行速度 - 时间曲线
根据速度-时间-位移的关系可得:

式(4)中,V限制j为第j个区间的限制速度;a为加/减速度,取±1 m/s2;其他符号意义同前。
结合式(3)、式(4),可解得V限制j≥43.9 km/h。
根据《广东省标准》第6.2.1条,列车通过平面曲线的最大速度可通过下式计算:

式(5)中,V为通过曲线的运行速度,km/h;R为曲线半径,m。
将V限制j≥43.9 km/h代入式(5)中,可得最小曲线半径R≥117 m。
4.1.3 最小曲线半径选取建议
《广东省标准》第6.2.3条规定“折返线、渡线、停车线、出入线、车场线、联络线等平面最小曲线半径不应小于15 m”。在实际情况中,在考虑荷载作用不均匀、材料性能、设计值与实际值的区别、施工质量等不确定性因素后,一般不采用极限值。另外,折返线、出入线对行车速度均有要求,采用极限值可能影响配线的功能进而影响线路的系统能力。根据《广东省标准》,道岔的最小导曲线半径均为20 m,侧向过岔速度均为15 km/h,从云巴厂家试验线的运行情况来看,车辆通过道岔的状态良好,因此,建议折返线、出入线等辅助线的最小曲线半径采用与道岔导曲线相同的标准。
正线最小曲线半径的选取应综合考虑运营效率,结合本文4.1.2节的分析,最小圆曲线半径R>117 m时可满足规范对旅行速度的要求。从全国各地云巴线网规划情况来看,线路平均站间距均大于600 m,因此下限速度可适当降低,建议选取40 km/h作为一般情况下的下限速度,对应的圆曲线半径R取100 m。结合《广东省标准》对最小圆曲线半径的规定,建议“正线上最小圆曲线半径一般情况下不宜小于100 m,困难情况下不小于30 m”。
4.2 车站范围内曲线最小半径
车站范围内曲线半径大小受站台边缘与车辆(车门处)的间隙控制,同时也受车体与站台门之间的间隙控制。《广东省标准》第6.2.4 条条文解释表明该条规定仅考虑了站台边缘与车辆(车门处)的间隙不小于180 mm,而未考虑站台门与车体之间的间隙要求。实践表明,忽略站台门与车体之间的间隙要求是不可取的,可能加大乘客困在站台门与车门之间的概率。本文基于站台门与车体之间的间隙要求,对车站曲线的半径选取进行研究。曲线车站分为凸型站台及凹型站台,如图5所示。

图5 站台加宽示意图
由图5可知,凸型站台站台门与车辆轮廓线之间的净距可按下式计算:

式(6)中,T为直线地段站台滑动门与车辆轮廓线之间的最小间隙;l为直线地段站台门的滑动门体与车辆轮廓线之间的最小间隙;W1为有效站台的建筑限界加宽值;W2为车辆位于曲线上的最大内移量。
凹型站台站台门与车辆轮廓线之间的净距可按下式计算:

式(7)中各符号意义同上。
对比式(6)及式(7)可知,凹型站台的曲线半径更为受限。下面以凹型站台为例进行分析。
根据《广东省标准》5.6.2条“站台门内侧最近点距轨道梁中心线不宜小于1 360 mm”及附表B.9(车辆轮廓线计算位置x坐标值为1 203 mm)可知,直线地段站台门的滑动门体与车辆轮廓线之间的最小间隙可按l= 1 360 -1 203 = 157 mm考虑。
凹型有效站台的建筑限界加宽值W1可按下式计算:

式(8)中,L为车辆计算长度,云巴车辆分为头车Mc与中间车M,头车长度为8.3 m,因头车悬挑部分采用曲线设计,建筑加宽时可不考虑该悬挑部分的加宽量,故车辆计算长度L取7 m;Z为车辆轴距,取4.2 m;R为曲线半径;H为云巴限界图中计算点的高度;h为车站曲线的实设超高率。
车辆停靠于凹型有效站台位置的内移量W2可按下式计算:
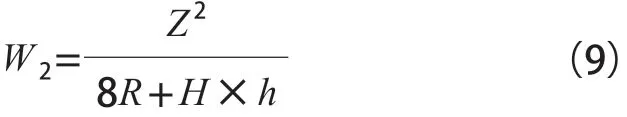
式(9)中各符号意义同上。
结合式(7)~式(9)可知,车辆停靠于凹型站台时,站台滑动门与车辆轮廓线之间的间距T可按下式计算:

根据GB 50157-2013《地铁设计规范》,间隙值T应按180 mm控制。经计算,满足间隙要求的凹型站台最小曲线半径R≥266 m。基于上述分析,建议站台范围内曲线的最小半径按300 m取值。
4.3 缓和曲线长度
缓和曲线长度的确定受许多因素影响,最主要是保证行车安全、平稳和旅客舒适条件。云巴的超高顺坡率主要由防倾覆系统引起,但其控制值较大,在缓和曲线计算中可以忽略,故缓和曲线长度可按下式计算:

式(11)中,LS为缓和曲线长度,m;V为设计速度,km/h;h为曲线实设超高率,%;hq为欠超高,%;f为滚动角时变率,取0.026 7 rad/s;b为未被平衡的离心加速度时变率,取0.35 m/s3;g为重力加速度,取10 m/s2。
由式(11)可知,缓和曲线的长度与实设超高率密切相关,超高率按下式计算:

式(12)中各符号意义同上。
在铁路设计中,未被平衡的超高使内外轨产生偏载,引起内外轨的不均匀磨耗,并影响旅客舒适度,因此一般情况下未被平衡的超高(欠超高或过超高)应尽可能小,则有恒大于,故在缓和曲线长度不受限的情况下有:

式(13)中各符号意义同上。
在实际工程中,特别在老城区等房屋密集区域修建云巴线路时,受工程条件限制,缓和曲线长度往往受限。另外受制梁工艺的影响,在云巴线路设计过程中应尽量避免竖缓重叠。过长的缓和曲线易对平、纵断面设计产生制约,不利于提高旅行速度。云巴线路结构与钢轮钢轨有明显区别,即便存在一定大小的未平衡超高时,所产生的超载也不会对轮轨结构产生较大的不利影响。因此,在缓和曲线长度受限时,建议在满足舒适度标准的前提下适当减小实设超高率,以达到提高通过速度的目的。下面以实例进行说明。
实例:半径R= 300 m,设计速度V= 60 km/h。
根据《广东省标准》,最大允许实设超高率8%,最大允许欠超高5%。根据式(12),h+hq≈9.4%。在一般情况下,为尽可能降低未被平衡的超高率,故取实设超高值为8%,代入式(11)可得LS= 50 m。在困难情况下,可将未被平衡的欠超高适当加大。取实设超高值为5%进行计算,代入式(13)可得31.3 m,此时,未被平衡的离心加速度为a= 0.44 m/s2<0.5 m/s2,未被平衡的离心加速度时变率b= 0.234 m/s3<0.35 m/s3,均满足要求。
5 结论及建议
(1)云巴的舒适度指标与TB 10098-2017《铁路线路设计规范》采用相同的指标,标准可相对提高或降低,以便于系统制式的推广。
(2)折返线、停车线、出入线等辅助线的最小曲线半径与道岔导曲线半径保持一致,取20 m;在一般情况下正线的最小曲线半径不宜小于100 m,困难条件下不宜小于30 m;车站的曲线半径设置应考虑屏蔽门安装的要求,最小曲线半径不宜小于300 m。
(3)云巴线路设计中,在缓和曲线长度受限的条件下,建议适当降低实设超高以提高线路上限通过速度。
