天津滨海新区轨道Z4线双线U型截面简支梁桥的自振特性分析

黄 欣，张京京，赵静波，石庆波，冀 伟,2

(1.中铁十八局集团有限公司， 天津 300222； 2.兰州交通大学， 甘肃 兰州 730070)

U型梁作为一种新型的桥梁结构，其主要由主梁和道床板组成，列车行驶在主梁之间的道床板上。相比于传统箱型截面梁式构件，U型梁因其桥梁高度小、降噪性能优异等优势，已成为铁路桥梁和城市轨道交通桥梁重要的形式之一。

国内外学者针对桥梁的动力特性方面做了大量的研究，聂建国等[1]利用势能驻值原理，综合考虑槽型梁弯曲、剪力滞效应以及扭转，推导出简支槽型梁在均布荷载作用下的解析解，并通过有限元软件进行验证；甘亚南等[2-3]通过研究剪力滞的方法，运用能量变分原理对槽型梁的动力特性进行了研究并与有限元结果进行对比，验证了该研究方法的有效性；周坚等[4-5]对剪力滞函数做了修正，利用余能原理推导出挠度的计算公式；倪元增等[6]通过构造翘曲位移函数，利用势能原理求解出应力以及挠度，并将结果与试验进行对比，验证了其正确性；宋晓东等[7]通过有限元模型以及薄壁杆件结构力学，考虑翘曲的影响，对U型梁的应力进行了深入的分析；雒敏等[8]利用空间板壳数值方法对单箱双室简支梁的剪力滞效应进行了分析，并将结果与有限元值进行了对比；Moon等[9]采用试验和有限元模拟相结合的方法对波形钢主梁组合箱梁的自振频率进行了参数化分析；冀伟等[10]利用能量变分法和Hamilton原理综合考虑剪力滞和剪切变形的影响，推导出波形钢主梁连续梁桥弯曲自振频率计算公式，并将计算结果与试验实测值以及有限元计算结果进行了对比；张云龙等[11]依据滑移理论和结构动力学思想，基于能量法推导出了考虑滑移效应组合梁的固有频率和振型；罗奎等[12-13]运用能量变分原理推导出波形钢主梁组合梁桥的单元刚度矩阵，利用Matlab软件编写出考虑剪切影响的该桥型的自振频率求解公式，并通过实测和有限元进行验证；Girhammar等[14]考虑层间滑移效应，采用变分法推导出了组合梁桥的振动频率公式；Feng等[15]用IAM方法对波形主梁组合梁桥的动力特性进行了系统的研究，并通过有限元软件对该方法的正确性进行了验证；陈卓异等[16]对4片波形钢主梁组合槽型梁进行两点对称加载，研究了截面的应力分布情况；柳春光等[17]基于简化辐射波浪法和混合法对大跨连续刚构在地震和波浪下的动力响应进行了分析；关孝文等[18]通过行车激励的方式对钢混叠合简支梁桥的动力性能进行了研究。

根据现有文献分析可知，对于U型梁的研究主要集中在静力特性方面，对动力特性的研究较少，且缺少相关的理论支持，因此本文运用能量变分原理对双线U型梁的竖向弯曲振动频率进行了研究，并建立ANSYS和MIDAS/Civil有限元模型进行对比分析，验证了理论计算结果的正确性和适用性。

1 工程背景

本文依托天津市滨海新区轨道Z4线一期工程项目，该结构主梁采用预应力混凝土U型组合连续梁结构，(35 m+50 m+35 m)双线U型连续梁梁长119.70 m，(30 m+50 m+30 m)双线U型连续梁梁长109.70 m，中支点截面中心处梁高4.89 m，中主梁较边主梁低0.2 m，跨中以及边跨直线段处梁高2.29 m，边支座中心线至梁缝中心线0.80 m，梁体沿着线路的中心线布置，U型截面梁横截面图如图1所示。

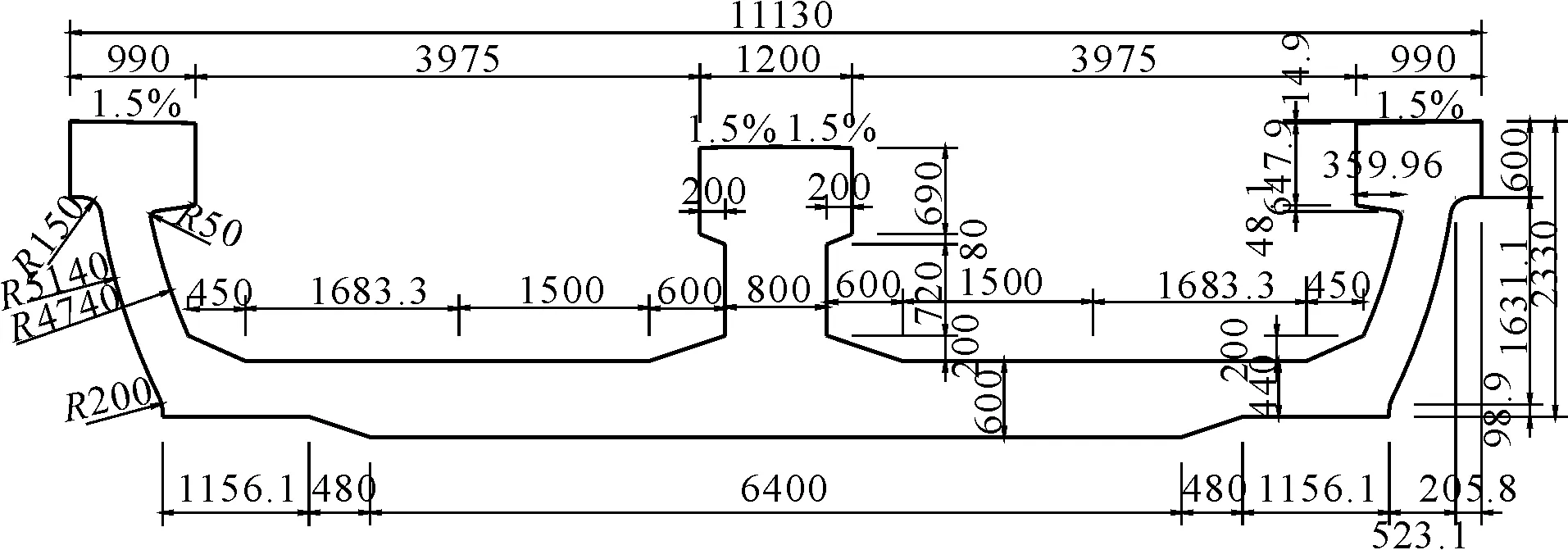
图1 U型梁横截面(单位：mm)

取边跨双线U型等截面为简支梁桥横截面，计算跨度取30.00 m，梁高2.49 m，桥梁全宽11.13 m，横断面布置为0.99 m边主梁+3.975 m行车道+1.200 m中主梁+3.975 m行车道+0.99 m边主梁=11.13 m。混凝土材料为C50，弹性模量Ec=3.45×104MPa，泊松比取0.2，重度取25.0 kN/m3。

2 方程的建立

2.1 能量变分法的基本假定

(1) U型梁在变形前后，均符合平截面假定。

(2) 忽略道床板由于剪力滞效应产生的横向应力[19-21]。

(3) 假定所有外荷载关于梁中心轴对称。

(4) 梁体材料只按混凝土考虑，忽略其他材料的影响。

双线U型截面简支梁桥横截面计算简图如图2所示，b为道床板长度的1/4长度，h1为截面的形心至道床板中心的长度，tb为道床板厚度，h为主梁高度，tf为主梁厚度，Ab为道床板面积，Af为主梁的面积，A为截面的总面积。

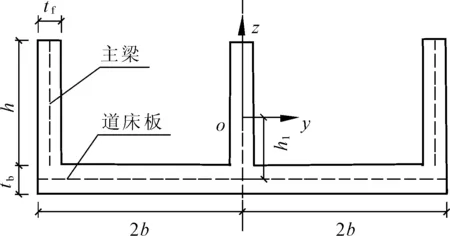
图2 1/2U型截面梁计算简图

研究该桥型的竖向弯曲振动频率时，需引入两个广义位移函数，即竖向位移函数ω和纵向位移函数v(x,y,t)：

(1)

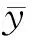
(2)

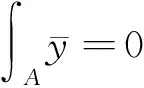
(3)

2.2 控制微分方程的建立

道床板应变能V1表达式为[22]:

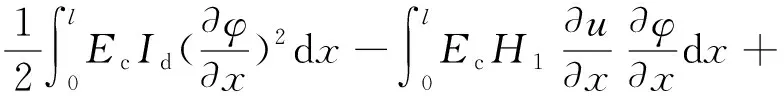
(4)

式中：Ec，Gc分别表示混凝土的弹性模量和剪切模量；Id表示道床板的惯性矩。H1，H2，H3的表达式为：

(5)

主梁应变能V2表达式为:

(6)

式中:If表示主梁的惯性矩。

双线U型截面简支梁桥在自由振动时的动能T为:

(7)

式中：m表示U型简支梁的单位长度质量。

利用Hamilton原理可得:

δ=δ(V1+V2-T)dt

(8)

将式(4)、式(6)和式(7)代入式(8)中，运用能量变分法的势能驻值原理可得到截面控制微分方程如式(9)—式(11)所示。

(9)

(10)

(11)

式中:I=Id+If,是双线U型梁截面惯性矩。

对式(9)求偏导可得:

(12)

(13)

(14)

对式(10)求偏导得:

(15)

(16)

将式(12)和式(13)代入式(15)可得:

(17)

将式(13)和式(14)代入式(16)可得:

(18)

对式(11)求三阶偏导可得：

(19)

将式(14)、式(17)和式(18)代入式(19)可得:

(20)

为计算式式(20)，引入自由振动时的竖向位移函数:

(21)

式中:ωn为U型梁自由振动时的圆频率；θn为U型梁自由振动时的初始相位角；Wn(x)为振型函数，可表示为：

Wn(x)=αnsin(nπx/l)

(22)

式中：常数αn[23]由初始边界条件决定，本文取αn=1。

根据式(20)、式(21)和式(22)和伽辽金法可得:

(23)

由式(20)可得U型梁自由振动时的表达式：

ωn=Θ·M

(24)

其中：

(25)

(26)

式中，n=1,2,3…;l为简支梁的跨度。

3 有限元模型

3.1 建立有限元模型

为了更准确的对比分析双线U型截面简支梁桥的竖向弯曲振动频率，采用ANSYS 19.0有限元软件和MIDAS/Civil有限元软件分别建立U型截面梁的三维实体模型。在ANSYS有限元模型中，主梁及道床板均采SOLID45实体单元模拟(见图3)，在MIDAS/Civil有限元模型中采用梁单元进行模拟(见图4)。双线U型截面简支梁桥的支座约束为：梁的一端采用固定铰支座，以约束横向、竖向及纵向三个方向的位移；梁的另一端采用滑动铰支座，以约束横向及竖向两个方向上的位移。

图3 ANSYS有限元模型

图4 MIDAS/Civil有限元模型

3.2 验证理论解析解

将本文竖向弯曲振动频率公式的计算结果与ANSYS有限元计算结果和MIDAS/Civil有限元计算结果进行分析对比，结果如表1所示。

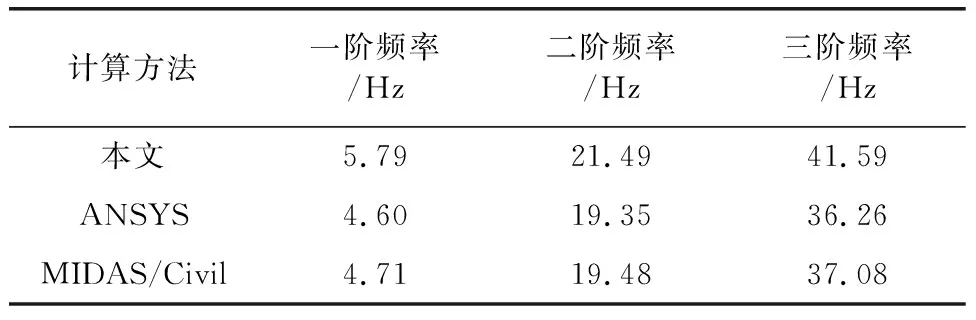
表1 不同方法下竖向弯曲振动频率比较

从表1可以看出，第一阶理论结果与ANSYS计算结果相对误差为6.56%，与MIDAS/Civil计算结果相对误差为4.32%；第二阶频率的理论解与ANSYS计算结果相对误差为9.17%，与MIDAS/Civil计算结果相对误差为6.23%；第三阶频率的理论解与ANSYS计算结果相对误差为11.13%，与MIDAS/Civil计算结果相对误差为9.43%。本文竖向弯曲振动频率计算公式计算结果与ANSYS有限元值的结果和MIDAS/Civil计算结果均吻合良好，精度较高，且随着结束的增大，计算误差也在增大，本文理论解析法更适宜求解低阶频率。

4 结构参数分析

4.1 宽跨比

为研究宽跨比对U型简支梁桥竖向弯曲振动频率的影响程度，其他条件与工程背景保持不变，仅改变计算跨度，分析其竖向弯曲振动频率。跨度分别取30 m、35 m、40 m、45 m、50 m，对应的宽跨比分别为0.322 4、0.276 3、0.241 8、0.214 9、0.193 4，由本文所推导的计算公式得到前三阶竖向弯曲振动频率如图5所示。

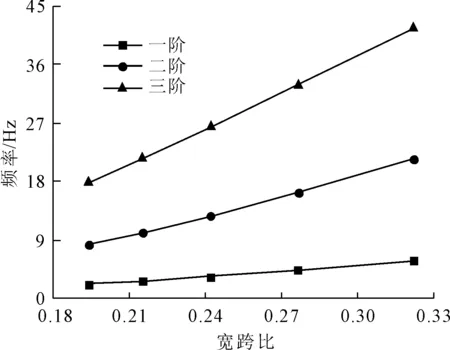
图5 宽跨比对竖向弯曲振动频率的影响

从图5可以看出，宽跨比会对双线U型简支梁桥的竖向弯曲振动频率产生影响，随着宽跨比的不断增大，竖向弯曲振动频率也逐渐增大，第一阶竖向弯曲振动频率最大增幅在35.03%；第二阶竖向弯曲振动频率增幅最高为31.85%；第三阶竖向弯曲振动频率增幅最高为26.62%；且随着阶数的不断升高，竖向弯曲振动频率的增幅在逐渐减小。

4.2 道床板厚度

为了研究混凝土道床板的厚度对双线U型简支梁竖向弯曲振动频率的影响，其他条件与工程背景保持不变，道床板厚度分别取：0.4 m，0.5 m，0.6 m，0.7 m，0.8 m进行对比分析。所求得的前三阶竖向弯曲振动频率的结果见图6所示。

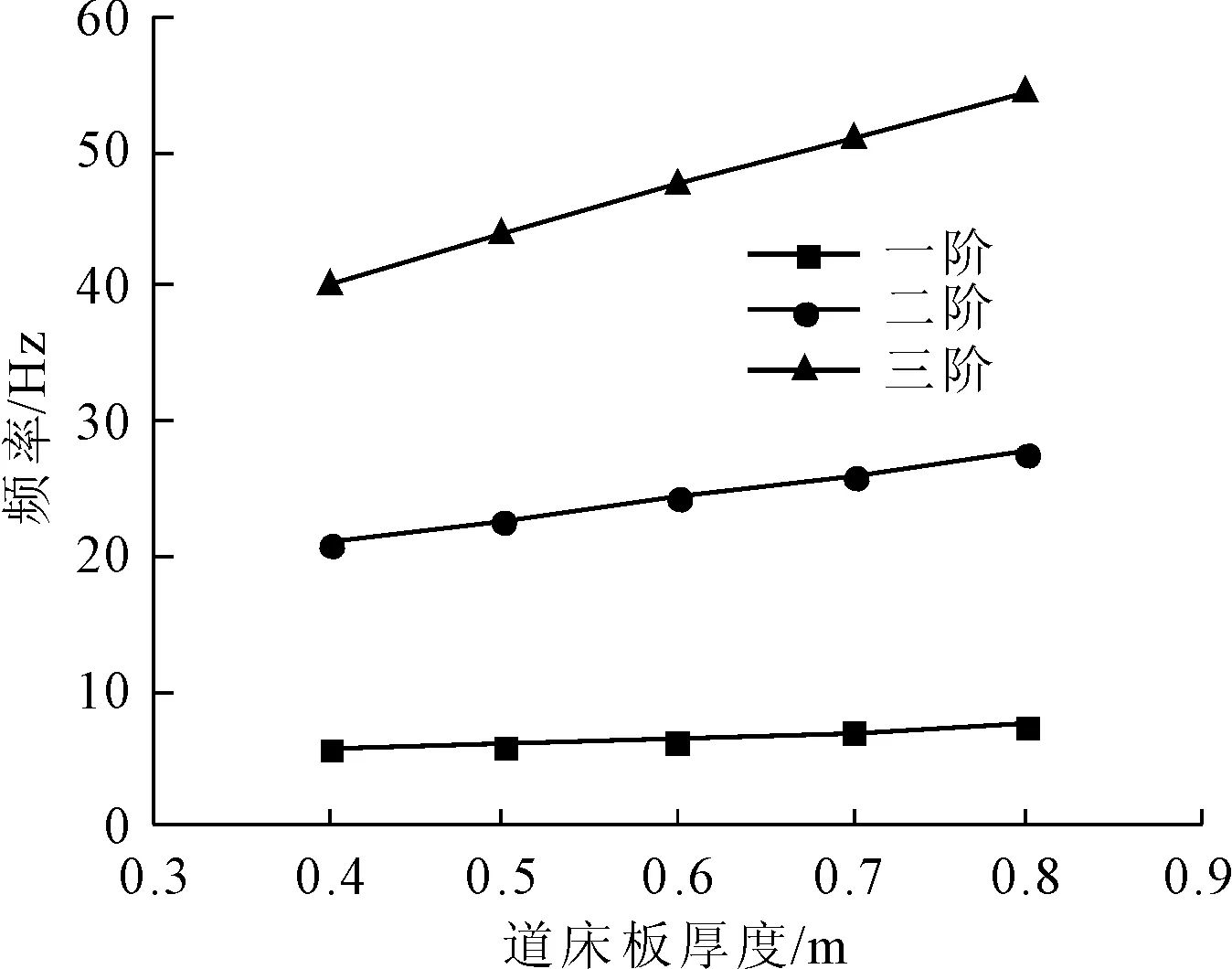
图6 道床板厚度对竖向弯曲振动频率的影响

从图6可以看出，道床板厚度的变化会对双线U型简支梁竖向弯曲振动频率产生影响，随着道床板厚度的不断增大，所求得的竖向弯曲振动频率在不断增大。第一阶竖向弯曲振动频率最大增幅为6.93%；第二阶竖向弯曲振动频率最大增幅为6.72%；第三阶竖向弯曲振动频率最大增幅为6.58%。且随着阶数的不断升高，竖向弯曲振动频率的增幅在不断减小。

4.3 高跨比

为研究高跨比对双线U型截面简支梁桥竖向弯曲振动频率影响程度，其他条件与工程背景保持不变，梁截面的高度分别取：2.1 m、2.2 m、2.3 m、2.4 m、2.5 m，其对应的高跨比分别为：0.070 0、0.073 3、0.076 7、0.080 0、0.083 3，由本文所推导的计算公式得到前三阶竖向弯曲振动频率如图7所示。

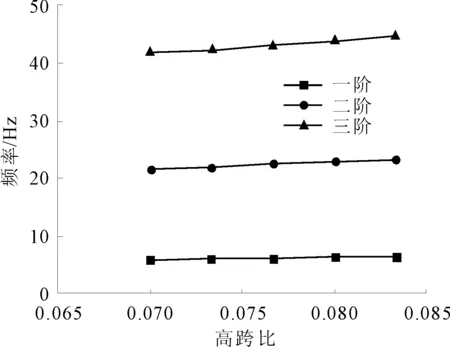
图7 高跨比对竖向弯曲振动频率的影响

从图7可以看出，高跨比的改变对双线U型简支梁竖向弯曲振动频率的影响比较小，影响幅度在2%左右，但整体上呈现增大的趋势。

5 结 论

(1) 利用能量变分法推导了双线U型截面简支梁桥竖向弯曲振动频率计算公式，发现竖向弯曲振动频率受多个因素影响，剪切变形会影响U型梁的竖向弯曲振动频率。

(2) 利用本文的竖向弯曲振动频率公式计算的结果与ANSYS结果和MIDAS/Civil结果吻合良好，验证了本文理论的正确性和适用性，且最大误差在10%左右，精度较高，可为类似桥型的竖向弯曲振动频率计算提供参考。

(3) 宽跨比会对双线U型截面简支梁桥的竖向弯曲振动频率产生较大影响，随着宽跨比的不断增大，竖向弯曲振动频率也逐渐增大，且对第一阶的影响最大，增幅为35.03%，随着阶数的增大，影响在逐渐减小。

(4) 道床板厚度的变化会对双线U型截面简支梁桥竖向弯曲振动频率产生较大影响，随着道床板厚度的不断增大，竖向弯曲振动频率在不断增大，且对第一阶的影响最大，增幅为6.93%，随着阶数的增大，影响逐渐减小；高跨比对双线U型简支梁竖向弯曲振动频率的影响较小，影响幅度在2%左右。