温度循环下能量群桩的热-力学特性数值分析

2021-07-21孙宇佳花永盛

水利与建筑工程学报 2021年3期

孙宇佳，花永盛，杨涛

(1.上海理工大学土木工程系，上海 200093；2.上海花样年房地产开发有限公司，上海 200000)

利用浅层地热的能量桩技术，克服了传统地源热泵技术中地埋管占地多和施工费高等缺点，不仅提高了换热性能而且节能环保，在世界各国的应用越来越多[1]。

国内外学者对于能量桩展开了一系列研究，已取得了较多有益成果。Laloui等[2]和Bourne-Webb等[3]分别在瑞士联邦理工学院和伦敦Lambeth学院进行了单能量桩现场测试，发现温度荷载引起的附加拉、压应力的数值较大。桂树强等[4]和路宏伟等[5]分别在河南信阳和江苏昆山进行了单能量桩热-力学响应的现场试验，研究了制热(冷)荷载或单个冷-热循环下单能量桩的桩侧阻力特性。一些学者[6-12]进行了砂土地基和黏土地基中单能量桩室内模型试验，研究了在冷-热循环与力学荷载共同作用下单能量桩和桩周土的热-力学响应，发现：(1) 桩头沉降随热循环产生累积，这种沉降累积在前几个热循环中完成；(2) 桩端约束对桩轴向应力和桩头竖向位移的影响较大；(3) 桩放热时地基土产生正超静孔压，桩吸热时地基土产生负的超静孔压；(4) 长期热荷载循环改变了桩-土界面的荷载传递特性。近年来兴起的多场耦合有限元数值模拟技术也用于单能量桩热-力学响应机理和长期热-力学特性的研究[13-19]。数值研究发现：(1) 温度荷载下桩-土相互作用主要取决于桩-土界面处摩阻力的发挥；(2) 桩头累积沉降桩是桩吸热时桩-土界面部分范围的剪应力达到其极限值所致；(3) 桩在放热时桩端约束对桩身应力的影响比桩吸热时要大；(4) 长期不平衡冷-热循环会影响热泵的运行效率。

能量桩总是以群桩的形式存在。单能量桩的研究无法反映能量桩之间热干扰效应。结合瑞士联邦理工学院校园储水池工程，Mimouni等[20]进行了力学荷载与温升荷载共同作用下桩-筏基础中西南角处三角形分布的4根端承能量桩热-力学响应试验。王言然等[21]进行了温升荷载下黏土地基中1×3能量群桩的热-力学特性现场试验。Peng等[22]进行了砂土地基中悬浮3×3能量桩-筏基础室内模型试验。Rotta等[23-24]采用三维有限元方法，对文献[20]中的能量群桩热-力学响应进行了数值模拟分析。从这些试验和数值模拟结果中可以发现：(1) 能量桩群的热-力学特性与单能量桩不同，能量桩群存在群桩效应;(2) 升温荷载下非能量桩的轴向压应力减小；(3) 筏板对能量群桩热-力学特性有较大影响。

较之单能量桩，能量桩群桩的工作机理要复杂得多，它受到群桩规模、能量桩数和布设方式、桩端约束、地基土种类等众多因素的影响。显然，现有的研究还仅仅是初步的，特别是饱和黏土地基中能量桩-筏基础热-力学特性的研究相对较少。有鉴于此，本文采用热-渗流-力三场耦合有限元法，模拟饱和黏土地基中悬浮7×7能量桩-筏基础中能量群桩的热-力学响应，研究力学荷载与长期冷-热循环共同作用下桩头沉降、桩身应力、地基土温度和地基土中超静孔压的变化和分布，为黏土地基能量桩-筏基础设计提供参考。

1 二维简化THM有限元模型

1.1 模型建立

饱和黏土地基中7×7能量桩-筏基础，桩的直径D=0.9 m，桩长Lp=20 m，桩间距s=3.6 m，正方形布置。正方形混凝土筏板厚度为0.5 m，边长为24 m。图1给出桩-筏基础平面图。

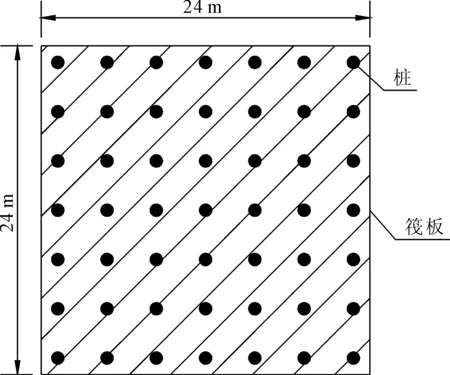
图1 能量桩-筏基础平面图

与砂土地基中能量桩-筏基础热-力学响应分析不同，饱和软土地基中能量桩-筏基础的热-力学响应是三维热-渗流-力(THM)三场耦合问题，采用三维三场耦合有限元分析非常复杂，数值计算也非常耗时。由于本文研究重点在于能量桩-筏基础的热-力学特性，将上述复杂的三维THM耦合问题简化为二维平面应变THM三场耦合问题进行分析。根据Dupray等[25]的方法，简化时需要进行如下换算：

(1) 将纵向7排空间不连续分布的能量桩简化为纵向连续分布的能量墙，墙的宽度等于桩的直径。根据变换前后竖向位移相等的原则，桩墙的弹性模量Eeq按下式计算：

(1)

式中：Ap和Ep分别为混凝土桩的截面积和弹性模量；L为筏板的纵向长度；n为纵向一排桩的数量。

(2) 考虑能量墙纵向热变形受到约束对其他方向热变形的影响，能量墙的线胀系数αeq按下式计算：

αeq=α(1+μ)

(2)

式中:α和μ分别为混凝土的线胀系数和泊松比。

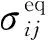
(3)

在二维能量桩-筏THM三场耦合有限元分析中，地基计算范围为80 m×40 m，即水平向取80 m，竖向取40 m。利用对称性，取一半区域建立有限元模型，见图2。模型的力学边界条件为：左、右边界竖向自由，水平向约束；下边界竖向和水平向均约束，上边界自由。模型的渗流边界条件为：左、右边界和下边界均不排水，筏板底面和地基表面排水。模型的热学边界条件为：左边界为对称轴，为热绝缘边界；右边界、下边界和地基表面均为恒温边界，数值为初始温度15℃。

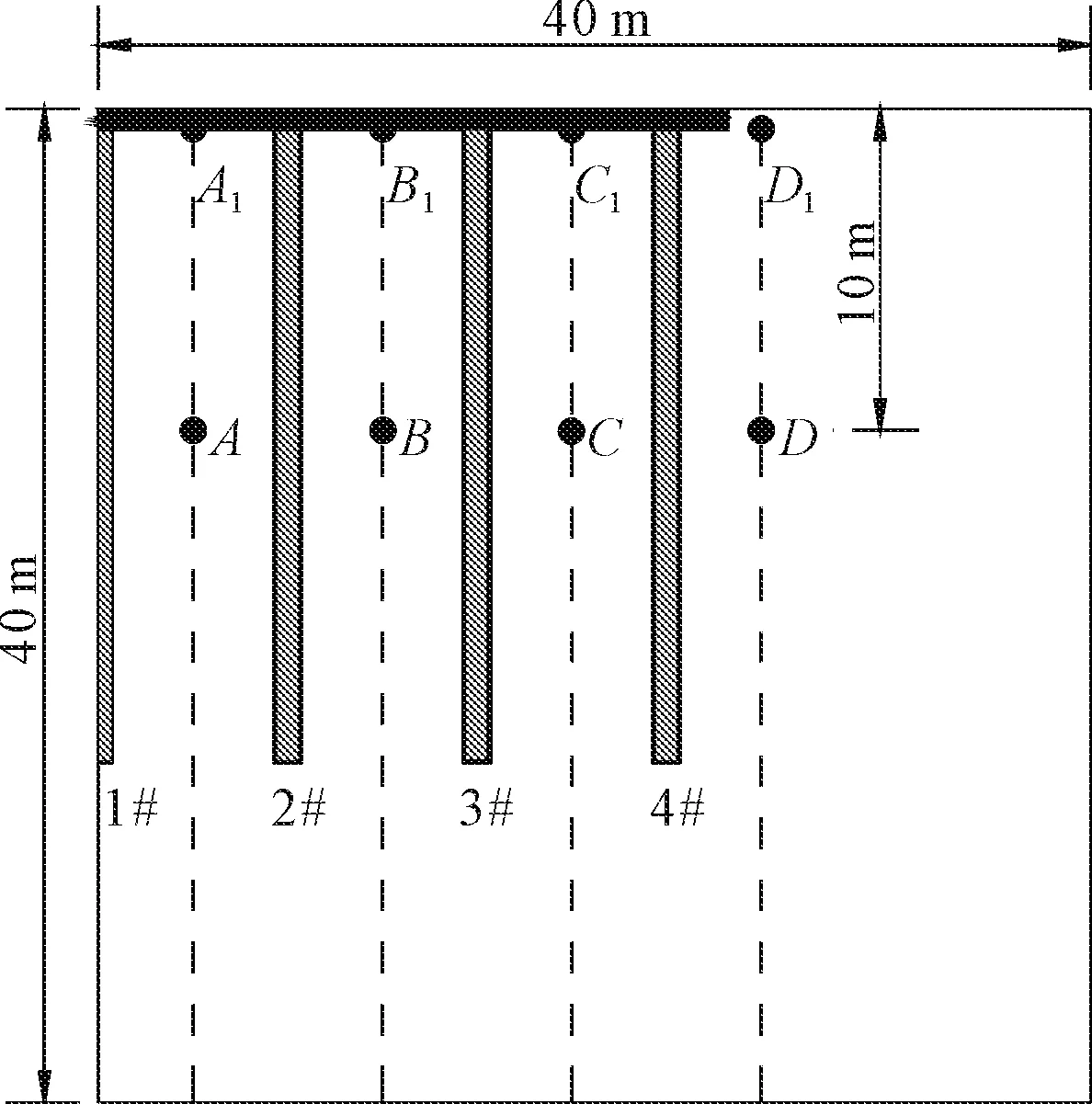
图2 2D有限元模型

在图2所示各排桩墙中，1#桩和4#桩分别为中桩和边桩，2#和3#桩都是内桩。A1、B1、C1和D1四个点位于桩顶平面，距地表0.5 m。A、B、C和D四个点均距地表10 m。A1A、B1B和C1C分别表示各桩间土中心线，D1D线在筏板以外，距4#边桩中心线1.8 m。

运用大型岩土工程软件PLAXIS 2D进行能量桩-筏基础THM三场耦合数值模拟计算。计算中桩采用热线弹性模型，地基土采用莫尔-库仑弹塑性模型。各材料的力学和热物性参数见表1。各材料均采用15节点三角形单元进行离散，离散后单元和结点数分别为4 025个和32 435个，有限元网格如图3所示。

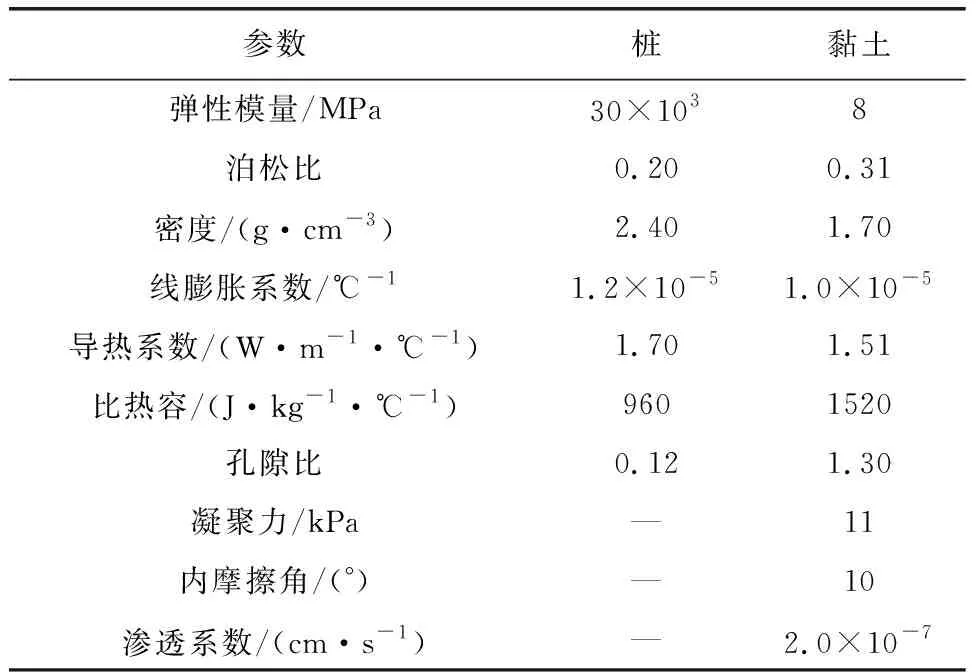
表1 材料热-力学参数

图3 有限元网格

在筏板上施加力学荷载，在能量桩上施加均匀分布的温度变化。筏板上均布荷载随时间线性施加，30 d后达到终值42 kPa，然后维持不变。为便于分析地基中温度荷载引起的超静孔隙水压力特性，待地基中力学荷载引起的超静孔压完全消散后在桩上施加温度荷载。能量桩上施加5个按正弦函数变化的冷-热温度循环，每个循环历经一年(360 d)时间，温度变化幅值为15℃。第一年中桩身温度变化曲线如图4所示，其表达式为：

(4)

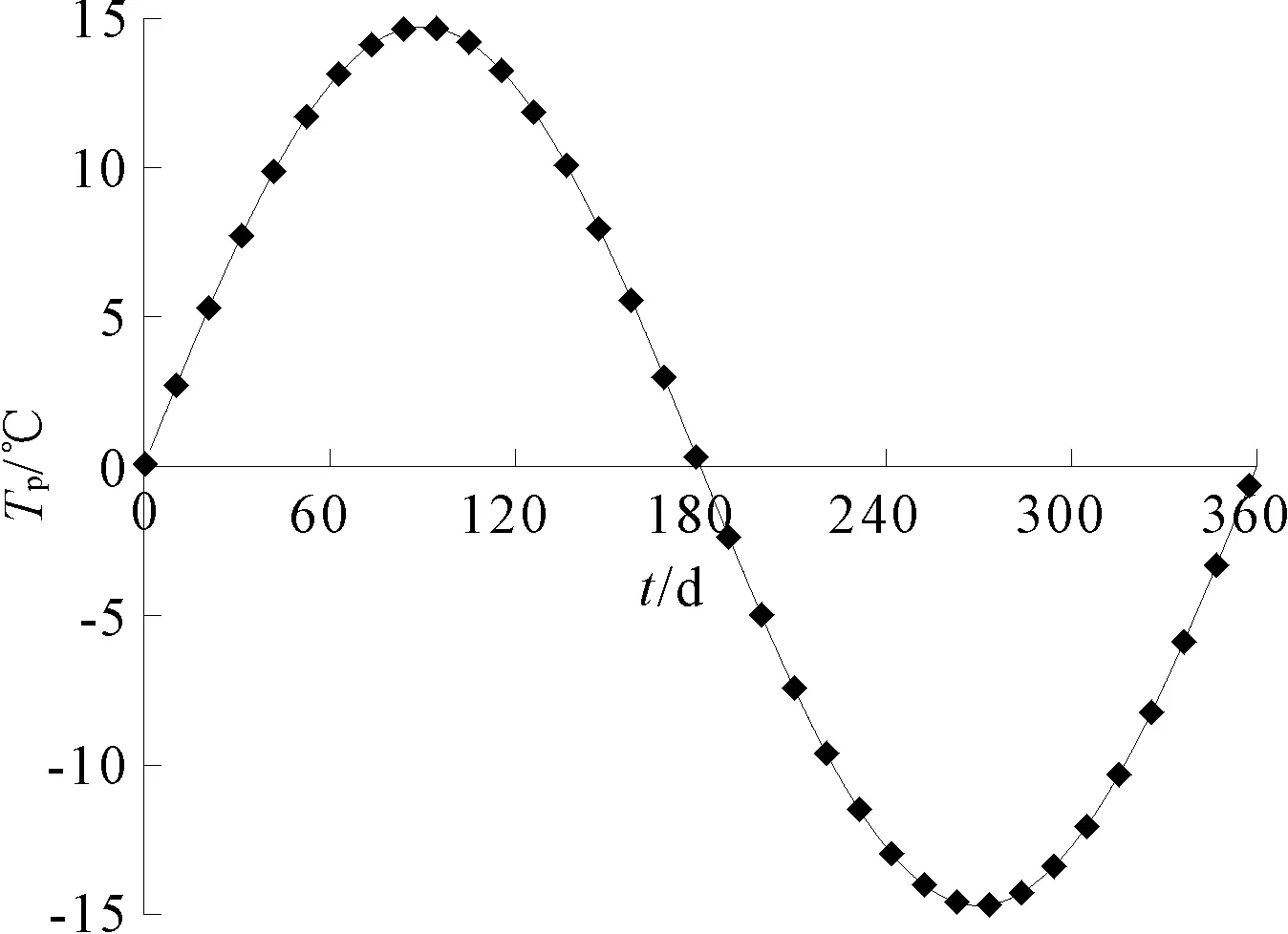
图4 冷-热循环中Tp-t曲线

1.2 有限元模型验证

Dupray等[25]利用前述简化二维有限元法分析了饱和黏土地基中7×15能量桩-筏基础的热-力学特性。桩长、直径和间距分别为20 m、0.8 m和7 m。筏板尺寸为117.0 m×51.6 m×0.5 m，其上均布荷载约为26 kPa。各材料初始温度均为11℃，能量桩承受5个一年内梯形分布的冷-热循环，最大吸热功率为245 W/m，最大放热功率为225 W/m。

地基土和能量桩均为线弹性模型，地基计算范围为151.6 m×70.5 m。采用与文献[25]相同的力学、孔压和热学边界条件，按本文前述方法建立能量桩-筏基础二维有限元模型，计算出一年内中心桩桩头竖向位移、中心桩侧9.5 m深处桩间土温度和热-力荷载引起的超静孔压随时间变化曲线与Dupray等[25]计算结果的比较见图5，图中正值桩顶位移表示桩头隆起，负值桩顶位移表示桩头沉降。

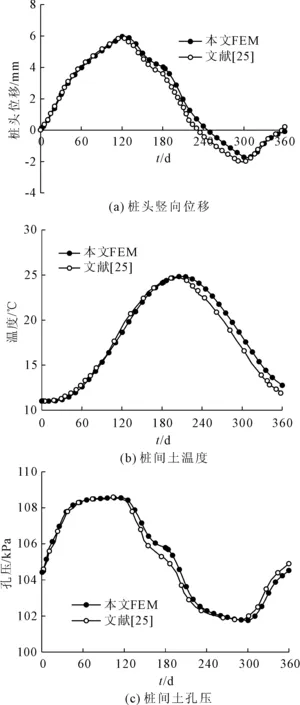
图5 与Dupray等数值结果的比较

由图5可见，本文有限元计算结果与文献[25]数值模拟结果有较好一致性，说明本文有限元模型能够用来进行能量桩-筏基础的二维THM三场耦合有限元数值分析。

2 能量桩-筏基础热-力学特性

2.1 群能量桩的热-力学响应

图6给出热-力学荷载共同作用下1#—4#能量桩桩头沉降随冷-热循环次数N变化曲线。由图6可知，各桩头沉降随温度循环的增加近似呈正弦曲线周期性变化，桩身温度最低时桩头沉降最大，桩身温度最高时桩头的沉降最小，中桩的沉降远大于边桩。各桩头沉降随温度循化而逐渐累积，1#—4#桩头累积沉降量分别为1.4 mm、1.5 mm、1.7 mm和2.1 mm，边桩桩头累积沉降量最大，中桩桩头累积沉降量最小。桩头沉降累积主要发生在第一个温度循环。此外，图6还表明，离筏板中心线越远，桩头竖向沉降的变化幅值越大，说明由温度荷载引起的边桩桩头的附加沉降(热-力荷载下的沉降减去力学荷载下的沉降)最大，中桩桩头的附加沉降最小。

图6 桩头沉降随温度循环变化曲线

图7给出热-力荷载下桩顶以下9.5 m处各能量桩轴向应力随温度循环变化曲线，负值表示压应力。从图7可知，各能量桩轴向压应力随温度循环近似按正弦曲线周期性变化。4#边桩的最大压应力和幅值最大，数值分别为259.3 kPa和79.8 kPa，1#—3#桩的最大压应力数值较为接近，分别为188.1 kPa、173.2 kPa和165.5 kPa，幅值分别为55.1 kPa、53.6 kPa和51.5 kPa。各能量桩的轴向应力不随温度循环而累积。

为得到各能量桩轴向应力分布特征，图8给出第5个冷-热循环中桩身温度最低(t=1 710 d)时各能量桩轴向应力沿桩长分布曲线。由图8可知，各桩轴向压应力沿桩长先增大后减小呈抛物线分布，4#边桩桩身压应力最大，3#桩的桩身压应力最小。1#—4#桩最大轴向压应力分别为155 kPa、137 kPa、117 kPa和242 kPa。

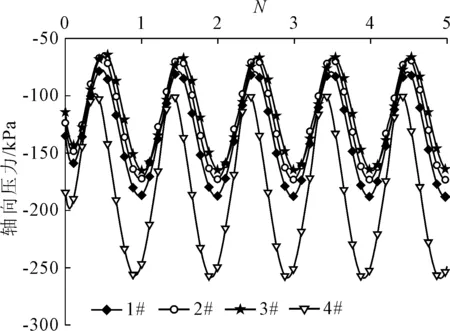
图7 能量桩轴向应力随温度循环变化曲线

图8 桩轴向应力沿桩长分布曲线(t=1 710 d)

2.2 地基土热-力学响应

图9给出地表下10 m处桩间土A、B和C以及筏板外D四个点的温度随温度循环变化曲线。由图9可知，这四个点的温度随温度循环近似呈正弦曲线变化。能量群桩内桩间土的A、B和C这三点的温度完全相同，在相同时刻达到其最高温度，数值均为26.6℃。筏板以外D点土的温度要低得多，其最高温度只有约21.1℃，较之桩间土减小了20.7%。计算还发现，土体的温度变化滞后于温度荷载的变化。例如，N=1时桩的温度在t=90 d时最高，而A(B和C)点和D点分别在t=140 d和t=146 d时才达到最大温升，分别滞后了50 d和56 d。

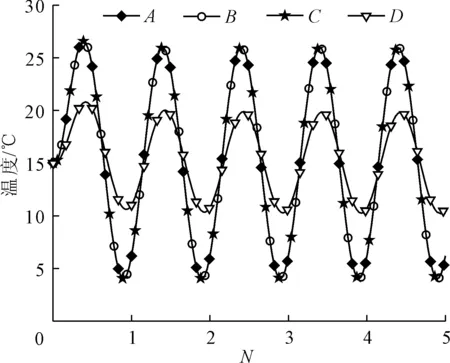
图9 地基土温度随温度循环变化曲线

图10给出了第5个冷-热循环中桩身温度最高时刻(t=1 530 d)桩间土中心线A1A、B1B、C1C三个截面和筏板以外D1D截面上温度沿地基深度分布曲线。由图10可以看出，A1A、B1B和C1C截面的温度不仅数值相同，而且除了桩两端附近外，在2.5 m～18.5 m深度范围内近似均布，平均值约21.6℃。筏板外侧土体的温度也有此特征，但数值明显低于桩间土，该范围内土体温度平均值约17.6℃。在桩端以下约深度4.3 m范围土体的温度略小于初始温度15℃，这是土体温度滞后于温度荷载的缘故。

图10 地基土温度沿深度分布曲线

图11给出A点的桩间土和筏板外D点地基土处由地基土温度变化引起的超静孔压随温度循环变化曲线。由于桩间土温度的变化相同，各相邻桩间土的超静孔压数值相等。由图11可知，升温引起正超静孔压，降温引起负的超静孔压，地基土超静孔压随温度循环呈正弦曲线周期性变化，超静孔隙水压力不随温度循环而累积。A点正超静孔压峰值约为29.1 Pa。筏板以外地基土的温度较低，超静孔压较小，正的峰值孔压仅为9.3 kPa。

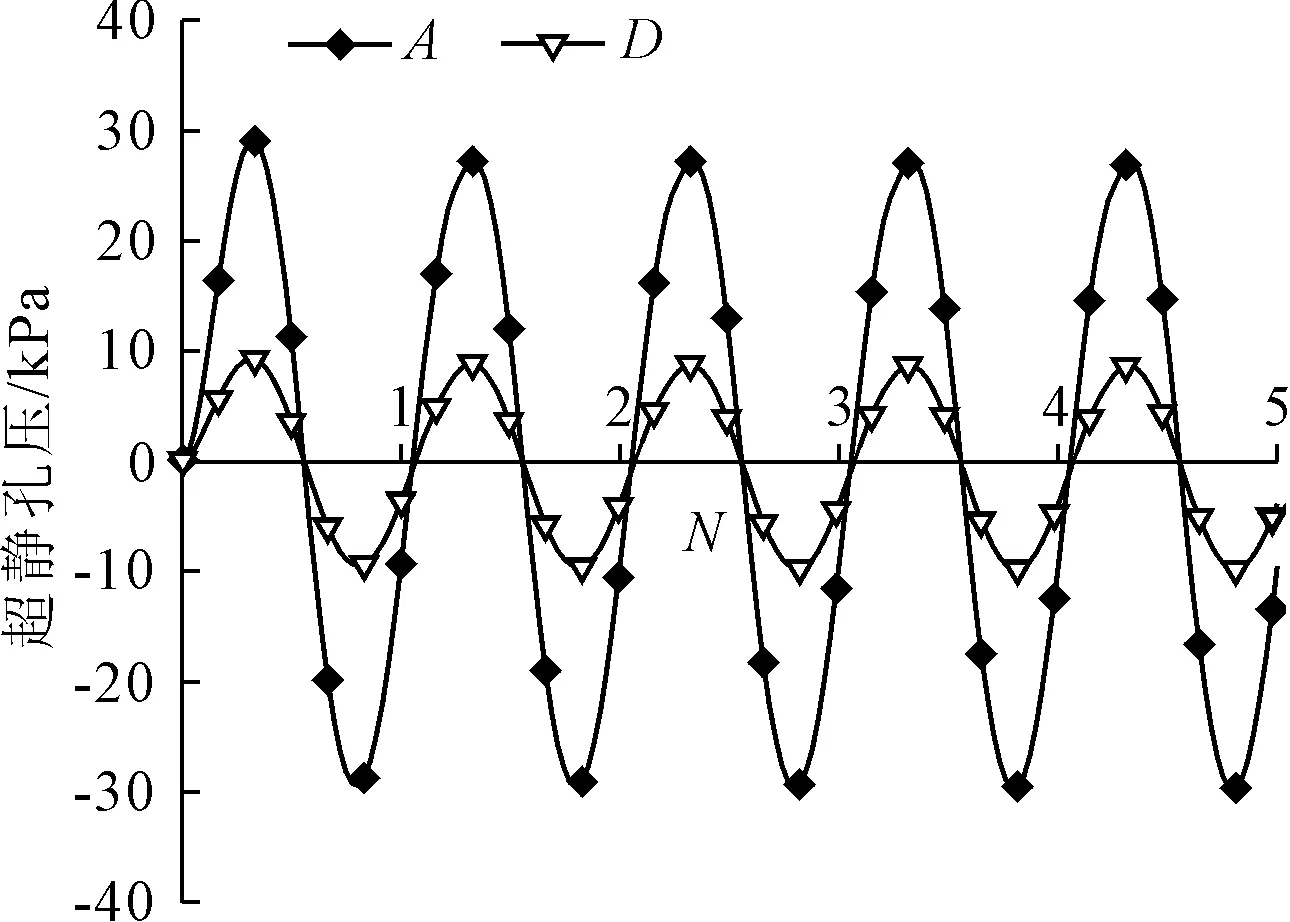
图11 地基土超静孔压随N变化曲线

2.3 群桩效应

为了研究温度荷载下能量桩-筏基础中的群桩效应，用有限元法计算出1#中桩在以下两种工况下第5个冷-热循环中温度最高时刻(t=1 530 d)的轴向应力分布曲线：工况1中群桩中只有1#中桩为能量桩，其他桩都是非能量桩工况，工况2中所有桩都为能量桩，计算结果如图12所示。从图12可以看出，升温荷载下 1#中桩为单能量桩(工况1)时其桩身压应力远大于所有桩都是能量桩(工况2)时它的压应力值。工况1下1#中桩最大压应力为250 kPa，工况2下1#中桩最大压应力为155.1 kPa，最大压应力下降了约38%。

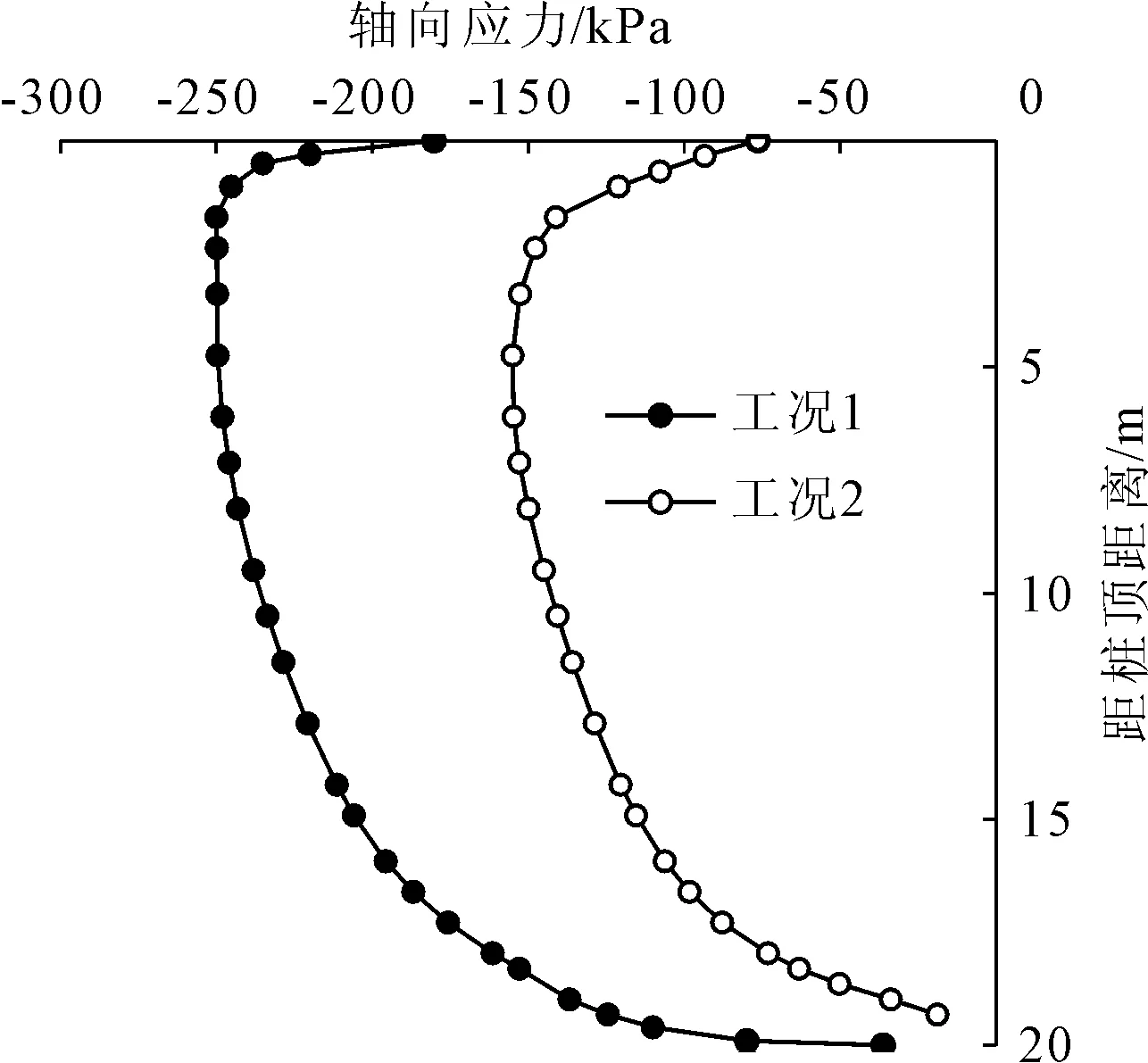
图12 两种工况下中心桩轴向应力分布曲线

表2给出这两种工况下各桩桩头的最大沉降Si(i=1～4)、筏板的平均最大沉降Sr和最大差异沉降△Sr。由于混凝土筏板刚度很大，取桩头最大沉降的平均值作为筏板平均最大沉降，取中桩与边桩最大沉降之差为筏板的最大差异沉降。从表2中可见，仅1#桩为能量桩时(工况1)筏板的最大沉降为48.6 mm，所有桩都是能量桩时(工况2)筏板最大沉降增大到53.1 mm，所有桩都是能量桩时筏板的最大沉降较大。筏板最大差异沉降则相反，所有桩都是能量桩时(工况2时)为4.9 mm，其数值为仅1#桩是能量桩(工况1)时的一半。上述计算结果表明，能量桩-筏基础具有明显的群桩效应，所有桩都是能量桩可减小单能量桩的轴向压应力，增大筏板的峰值沉降，减小筏板峰值差异沉降。