中字形变径水泥土搅拌桩复合地基固结分析

黄财明,杨 涛，盛志成

(上海理工大学 土木工程系，上海 200093)

目前，水泥土搅拌桩复合地基已成为世界各国处理软土地基最常用的一种方法。实践表明，无论采用“干法”和“湿法”施工，传统的水泥土搅拌桩(DCM桩)成桩质量都难以控制，导致其单桩和复合地基的竖向和水平向承载力均较低，复合地基呈现桩头压碎和桩身弯曲破坏等破坏模式。为解决这一问题，东南大学刘松玉教授科研团队提出了基于双向搅拌技术的新型水泥土搅拌桩-变径水泥土搅拌桩[1]。根据桩的扩径段所处位置，变径水泥土搅拌桩分为二种类型[2-3]：一是扩径段位于桩顶部的钉形搅拌桩，二是扩径段位于桩顶以下的中字形搅拌桩(CDCM桩)，也常称为“变径搅拌桩”以区别于钉形搅拌桩。

朱志铎等[4]和Yi等[5]通过现场标惯、取芯和载荷试验，发现钉形搅拌桩成桩质量、强度优于DCM桩，其复合地基和单桩的承载力都远大于DCM桩复合地基和DCM桩。吴加武[6]通过对实际工程的研究，证明了DCM桩作为一种海上软土地基加固体，对提高软土地基抗剪强度及地基承载力是有效可行的。刘松玉等[7-8]和Yi等[9]进行了钉形搅拌桩和DCM桩复合地基在路堤荷载下的现场和室内对比试验，发现：钉形搅拌桩分担的荷载远大于DCM桩，钉形搅拌桩复合地基的沉降、超静孔隙水压力和坡脚下地基土水平位移均小于DCM桩复合地基。曹洋等[10]通过有限元数值模拟，研究了路堤荷载下钉型水泥土搅拌桩的桩身受荷模式、桩体加固机理及稳定性。易耀林等[11-12]采用三维数值模拟方法，在路堤荷载下分析了悬浮钉形搅拌桩复合地基的竖向附加应力分布和沉降特性，较之DCM桩复合地基，钉形搅拌桩复合地基加固区压缩量和桩-土差异沉降都会变小，而下卧层沉降增大。Phutthananon等[13]利用轴对称有限元法，在等体积条件下研究了扩大头的桩身强度及几何尺寸对钉形搅拌桩破坏模式和竖向承载力的影响。

中字形变径搅拌桩适宜加固软土层位于地基中部的多层软土地基。易耀林等[14]通过现场取芯和载荷试验发现，中字形搅拌桩的强度远高DCM桩，其单桩极限承载力是DCM桩的3～5倍。刘松玉等[15]通过现场试验发现：路堤荷载下DCM桩复合地基与较大间距的中字形搅拌桩复合地基有相同的加固效果，后者更为经济。易耀林等[16]采用三维有限元法，研究了路堤荷载下中字形搅拌桩复合地基减小最终沉降的机理。研究发现：中字形搅拌桩加固可显著减小扩径段周围软土的压缩量，但扩径不会影响坡脚下地基土的水平位移。

尽管变径搅拌桩复合地基承载变形特性的研究已取得了较多成果，但其设计理论研究才刚刚开始。易耀林等[17]提出了计算钉形搅拌桩复合地基最终沉降的“广义承台法”。杨涛等[18-19]给出了计算端承和悬浮钉形搅拌桩复合地基固结度的解析计算式。此外，易耀林等[14]提出了中字形搅拌桩单桩承载力计算方法。尽管如此，目前还尚未有中字形搅拌桩复合地基固结计算方法的研究成果报道。有鉴于此，本文对此问题展开研究，目的是建立中字形搅拌桩复合地基固结解析解，并给出CDCM桩复合地基固结的影响因素。

1 固结模型及基本假定

图1所见为CDCM桩复合地基固结模型，z是竖向坐标，r是径向坐标。单桩影响区半径为re，上、下部小直径搅拌桩的半径均为rp1，长度分别为H1和H3，压缩模量分别为Ep1和Ep3，置换率为m=(rp1/re)2。扩径桩位于变径桩的中部，其长度和半径分别为H2和rp2，压缩模量为Ep2。中部扩径桩与小直径桩的桩径比为ρ=rp2/rp1，相应地，中部扩径桩置换率为mρ2。复合地基总厚度为H=H1+H2+H3。根据中字形搅拌桩各部分的长度，将复合地基加固区划分为上、中、下三层，其厚度分别为H1、H2及H3。kv1、kv2、kv3和Es1、Es2、Es3分别为三层加固区桩间土的竖向渗透系数及压缩模量。p(t)为施加在复合地基表面的均布荷载。

图1 轴对称固结模型

下面公式推导采用了如下基本假定：

(1) 桩间土完全饱和，土中水的渗流服从达西定律。

(2) 桩体不排水，荷载作用下内部无超静孔隙水压力产生。

(3) 扩径桩以下土体只发生向外的径向渗流。

(4) 等应变假定成立。

(5) 土中渗透系数和压缩模量为定值，不随固结过程变化。

(6) 由荷载引起的附加应力沿深度方向均布。

2 固结方程和定解条件

2.1 固结方程

根据文献[18]的研究，写出变中字形搅拌桩复合地基上、中、下加固区桩间土的固结方程：

(1)

(2)

(3)

(4)

2.2 定解条件

考虑PTIB边界(即底部不排水、表面排水)情况，则其定解条件如下：

(1)竖向边界条件：

(5)

(6)

(2)加固区分界面处孔压和水流连续条件如下：

①z=H1:

(7)

(8)

②z=H1+H2:

(9)

(10)

(3)变荷载作用的初始条件如下：

(11)

3 固结解析解

3.1 固结方程与定解条件的函数变换

直接在定解条件式(5)—式(11)下求解控制方程式(1)较为困难。为便于求解，参照Gong等[20]的方法进行如下的函数变换式：

(12)

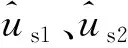
(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

3.2 固结解析解

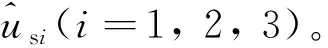
为使公式表述简洁，引入下面5个无量纲参数：

(21)

Ees1=(1-m)Es1+mEp1

(22)

Ees2=(1-mρ2)Es2+mρ2Ep2

(23)

Ees3=(1-m)Es3+mEp3

(24)

式中:Eesi(i=1, 2, 3)为第i加固区的复合压缩模量。

参照谢康和等[21-22]的研究，可以推导出中字形搅拌桩复合地基各加固区的平均孔压：

(25)

(26)

(27)

λn是以下特征方程的根：

Rn+d3ctg(μ3c3λn)Vn=0

(29)

(30)

Ani和Bni(i=1, 2, 3)按下面递推公式计算：

[An1Bn1]T=[1 0]T

(31)

(32)

(33)

(34)

(35)

(2) 单级加荷下的固结解析解。σ(t)为均布竖向附加应力随时间的变化曲线，荷载单级施加时，如图2所示，显然，有：

(36)

将式(36)代入式(25)再利用式(12)可推导出单级荷载下中字形搅拌桩复合地基桩间土的平均超静孔压：

图2 σ(t)-t曲线

① 0≤t≤t1：

(37)

②t≥t1：

(38)

(39)

利用式(12)计算出各加固区的超静孔压，代入式(34)和式(35)即可得到单级荷载下中字形搅拌桩复合地基的整体平均固结度如下：

(40)

(41)

4 算例验证

4 m高路堤下中字形搅拌桩复合地基的厚度为H=16 m，路堤土的重度为17 kN/m3。上、下部小直径桩段半径rp1=0.25 m，长度分别为H1=3 m和H3=9 m，扩径桩段的半径和长度分别为rp2=0.5 m和H2=4 m，扩径比ρ=2。单桩影响区半径re=1.2 m，小直径桩段置换率为m=0.04。

固结模型具有轴对称性，选图1的1/2建立有限元模型，如图3所示。限制模型左右边界法向位移，限制底部边界法向和切向位移，上部边界自由，允许排水。有限元模拟过程中采用线弹性模型模拟各材料，所用材料的具体参数见表1。压缩模量E和弹性模量E0间的近似转换利用式E0=(1+μ)(1-2μ)E/(1-μ)近似估算[23]，μ是泊松比。

图3 有限元网格

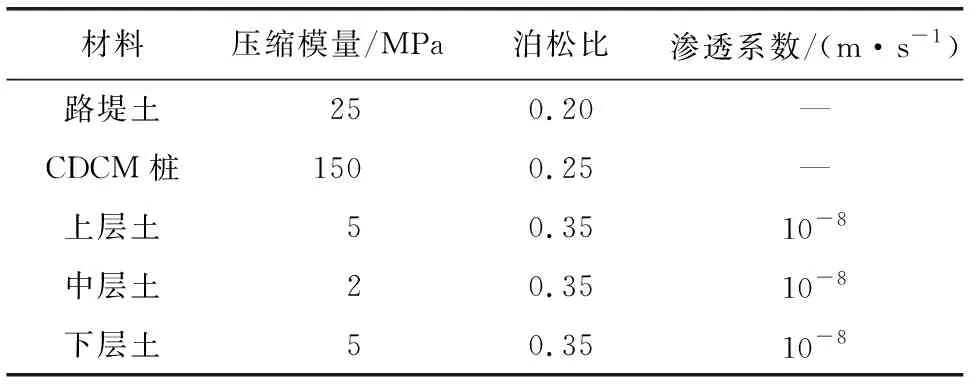
表1 数值模拟用的材料参数

采用大型有限元软件ABAQUS进行复合地基固结分析。路堤单级填筑，填筑时间t1=120 d。有限元分析中，分别选用CAX4(4结点4边形)和CAX4P(4结点孔压-应力耦合)单元对填土路堤、CDCM桩和桩间土进行网格划分处理，单元总数为2 164个，结点总数为2 335个。

图4比较了固结度解析解和有限元解获得的中字形搅拌桩复合地基按沉降定义的固结度Us随TE变化曲线，TE=cvt/H2为无量纲时间因数，cv=Eskv/γw为桩间土的固结系数，kv和Es为桩间土的竖向渗透系数和压缩模量。

图4 固结度解析解与FEM解的比较

从图4中解析解和FEM的固结度比较可知，二者结果间的差值较小，说明采用本文解析解得到的CDCM桩复合地基固结度解答计算精度满足要求。

5 复合地基固结性状分析

为研究中字形搅拌桩复合地基的固结性状，采用本文固结解析解进行参数影响分析。基准参数如下：复合地基厚度H=16 m，上、下部小直径桩的长度分别为H1=3 m和H3=9 m，半径均为rp1=0.25 m。中部扩径桩的长度和半径分别为H2=4 m和rp2=0.5 m。单桩影响区半径re=1.2 m，ρ=2。均质中字形搅拌桩的压缩模量为Ep1=Ep2=Ep3=Ep=150 MPa，桩间土压缩模量为Es1=Es3=5 MPa，Es2=2 MPa。各层桩间土的渗透系数kv1=kv2=kv3=10-8m/s。荷载p=68 kPa单级施加，加荷历时t1=120 d。

(1)桩身刚度影响。图5给出CDCM桩压缩模量Ep的变化对复合地基固结速率的影响，图中横坐标采用无量纲时间因数Tu=cv1t/H2。此外，考虑中部扩径桩段刚度大于小直径桩段刚度的情况，图6给出扩径桩段不同压缩模量Ep2下复合地基的固结度曲线。

图5 Ep对固结速率的影响

图6 Ep2对固结速率的影响

图5和图6表明，复合地基的固结速率随中字形搅拌桩和其中扩径桩段压缩模量的增加而增大，这说明整个中字形搅拌桩或其中部扩径桩的刚度越大，中字形搅拌桩复合地基的固结越快。比较这两幅图还可以发现，中部扩径桩刚度的增加对复合地基固结速率的影响较小。

(2)小直径段置换率的影响。图7给出中字形搅拌桩中小直径桩段的置换率m的变化对复合地基固结度曲线的影响，此时中段扩径桩的直径rp2=1.0 m保持不变。

图7表明，中字形搅拌桩复合地基的固结速率，随小直径桩段的置换率增加而增大，但其增加率逐渐减小，m≥0.04以后其数值的增加对复合地基固结速率影响很小。

(3) 扩径桩段几何尺寸和位置的影响。图8给出中部扩径桩段不同扩径比ρ下复合地基固结度曲线的比较，此时小直径桩段的半径rp1=0.25 m保持不变。从图8中可见，不同扩径比下的固结度曲线近乎重合，说明在扩径比ρ≤2.2范围内其数值的变化对复合地基固结速率没有影响。

图7 m对固结速率的影响

图8 ρ对固结速率的影响

图9给出扩径桩段长度H2的变化对复合地基固结度曲线的影响，计算中保持扩径桩段顶面距地表距离H1=3 m不变。从图9中可以发现，随着扩径桩段长度的增加，复合地基固结速率逐渐增大。

图9 H2对固结速率的影响

图10给出扩径桩段位置的变化对复合地基固结度曲线的影响，计算中扩径桩段长度H2=4 m保持不变。扩径桩的位置可用其顶面到地表的距离H1表示。当H1=0时，中字形搅拌桩变为钉形搅拌桩。从图10中可以发现，复合地基的固结速率随着扩径桩段位置的逐渐下移而增大，但增加的幅度不大。

图10 H1对固结速率的影响

6 结 论

建立了端承中字形变径水泥土搅拌桩复合地基固结解析解，利用固结度解析解获得了主要因素对复合地基固结速率的影响。主要结论如下：

(1) 数值算例表明，所建立的中字形搅拌桩复合地基固结解析解具有足够的计算精度。

(2) 中字形搅拌桩复合地基的固结速率随小直径桩段置换率、整个桩体压缩模量、扩径桩段长度和压缩模量的增加而增大。

(3) 中字形搅拌桩复合地基的固结速率随扩径桩位置的下移而略微增大。

(4) 扩径桩段直径的变化对中字形搅拌桩复合地基的固结速率没有影响。