基于模糊C-均值聚类算法的台区电压与用户关系辨识

2021-07-21曾顺奇吴杰康蔡志宏

四川电力技术 2021年3期

曾顺奇，吴杰康，李欣，蔡志宏

(1.广东电网有限责任公司广州供电局，广东广州 510000；2.广东工业大学自动化学院，广东广州 510006)

0 引言

近年来，随着中国城乡经济建设迅猛发展，用电负荷激增，有些小用户发展成为大功率用户，超过了线路本身预留的空间，导致台区电压在用电高峰出现欠压现象[1]。配电网网架结构的相对滞后和迅速增长的用电需求之间的矛盾越来越突出[2]，导致台区电压波动较大，严重影响用户用电体验并降低配电网供电可靠性，给供电公司带来了严峻的考验。针对以上问题，业界学者开展了针对性研究，例如：从原理上对低压问题产生的原因深入分析，得到电压偏低的原理[3]；构建多指标的台区低电压成因识别指标体系，建立基于支持向量机多分类器的台区低压成因识别模型[2]；通过人工排查、登记、数据预测和定期分析低电压，动态识别低电压[4]；采用改进粒子群优化(particle swarm optimization, PSO)算法优化电容配置，改善负荷接入配电网对电网造成的冲击[5]。

以上文献从低电压成因以及治理方案进行相关研究，但是充分利用大数据技术识别台区电压与用户用电行为之间关系相关研究较少。因此，提出一种新的方法辨识台区电压与用户的关系：通过智能电能表提供的海量用电数据，首先，利用插值法对数据采样过程中产生的缺值进行补全；然后，对其进行数据特征提取，通过主成分分析法(principal component analysis, PCA)进行数据降维，大大减少计算量，提高辨识的时效性和聚类的收敛性；最后，采用模糊C均值(fuzzy C-means, FCM)算法对用户进行分类，按照周期内用户用电有功值分为大、中、小3个等级用户，并结合皮尔逊相关系数分析各个等级用户在峰-谷-平区间对台区电压的影响水平，进而确定不同负荷等级用户与配电台区电压之间的关系。

1 台户关系

1.1 台户拓扑结构

配电网终端由变压器、配电箱和配有智能电能表的用户端组成。一般每一个智能电能表箱都有三相进线，由智能电能表箱分出A、B、C三相连接各个用户，一个智能电能表箱下可能存在单相用户，也有三相用户，这里只讨论单相下的所有用户。相与相之间电压互不影响，每一相只受该相所接用户的用电情况影响，具体的台户拓扑结构如图1所示。

图2为台户等值电路，图中Μ3点为变压器A相低压侧电压。通常低压侧的电压与用户用电功率、高压侧挡位和负荷功率有关。高压侧的挡位分别为±5%和0。由潮流计算可得Μ3点的电压：

图2 台户等值电路

VM3=VM1-ΔV

(1)

(2)

下面主要研究在台户关系中，不同用户的用电行为对应的峰-谷-平区间与导致变压器低压侧电压发生偏移二者之间的关系。

1.2 台户关系

一个台区下某一台变压器中一条单相线路连接了不同用电等级的用户，其中某一些用户的用电行为在峰-谷-平期影响变压器低压侧电压，使其产生波动。研究用户用电与台区变压器低压侧电压波动之间的关系是基于台区和用户的历史数据。用户有功功率数据由智能电能表获取，采集终端的时间分辨率为15 min，采集时长为7 d，共有672个用户侧有功功率数据点。从用电采集系统历史数据中获取并构建台区用户有功功率的数据矩阵X∈RN×D：

(3)

式中：X为N个用户在采集区间内D个采样点所组成的矩阵；xi,tj为台区用户i在tj时刻的有功功率测量值；N为台区下的用户总数；D为采样时段内台区用户有功功率的采样点数，即台区用户原始有功功率数据集的特征维度。X的列向量Xtj为台区用户在tj时刻的有功测量向量；X的行向量Xi为单个台区用户i在采集时段内的有功测量向量，其单位为kW。

假设以上N个用户均属于同一个台区下某个变压器的A相，按照D=96×7获取A相电压数据，构成变压器低压侧电压时间序列矩阵：

V=[vt1,vt2,…,vtD]

(4)

式中：V为变压器低压侧A相在采集周期内的电压向量；vtD为该相D时刻的测量电压值。

2 台户数据处理与修补

2.1 功率缺值修补的插值法

智能电能表采集数据时间跨度大，用户的原件安装、调试可能存在差异，加之停电或者采集失败等因素，往往容易导致采集到的电力数据出现缺失现象。由于同一用户有功数据与时间呈线性关系，可采用相邻点(tt-1,xi,t-1)与(tt+1,xi,t+1)估计中间点的值。假设xi,t=f(t)呈线性关系，通过已知的两点代入线性方程估算缺值xi,t。

2.2 台户数据的皮尔逊相关系数

应用皮尔逊相关系数分析负载与台区间电压的关系。现有台区D个时间点的电压数据：V=[v1,v2,…,vD]。由RN×D通过皮尔逊相关系数计算公式计算各个用户与台区电压之间的关联程度。

皮尔逊相关系数计算式为

(5)

式中：Ε(·)为该向量的期望值；cov(·)为两个向量的协方差；ρ(V,Xi)取值范围为[-1，1]，小于0时为负相关，大于0时为正相关，当且仅当V与Xi有严格线性关系时取±1。

表1为基于皮尔逊相关系数的相关强度估计，通过表1相关系数范围判断变量之间的相关强度。

表1 基于皮尔逊相关系数的相关强度估计

2.3 数据降维处理的主成分分析方法

在采集设备覆盖率和采集成功率较高的台区,采集的有功数据往往分布较为集中，但是采集数据大多精度不高而且存在噪声或者冗余。因此，不能简单使用加权平均法或者求和的方法进行用户等级区分。需要对采集到的数据特征进行进一步挖掘。可以采用PCA方法进行数据的特征提取和降维处理。经过降维处理后的数据，仍保留原始数据的分布特性。高维数据在数据分析中计算量大，时效性能不好，利用模糊聚类算法对用户等级分类时可能会出现维度灾难、计算量大、计算时间长等问题。通过PCA法缓解这些问题，尽可能解释变量具有相关性的高维数据集。通过计算数据的协方差矩阵cov(X)，寻找一个能反映出原有数据特征95%的特征矩阵，将原始高维空间过渡到低维空间，实际将数据映射到一个低维子空间，降维成一个线性无关的低维数据集。PCA具体分析过程可参考文献[10]。

PCA数据降维的具体步骤如下：

1)对原始数据矩阵X进行转置处理得到XT，得到的矩阵行表示每一个用户tj时刻的特征，共有D维特征。对XT零均值处理得到矩阵X′为

(6)

2)使用线性变换得到协方差矩阵为

(7)

3)通过求解|λI-R|=0得到特征值λ。最后计算特征值的累计贡献率[10]：

(8)

式中，βi为累计大于95%特征值组成成分(λ1,λ2,…,λk)。对数据进行分析后得到k值。同时得到特征值对应的特征矩阵UD×D=[u1,u2,…,uD 1]。提取前k个特征值对应的特征向量组成降维矩阵UD×k。降维矩阵Zn×k可表示为

Zn×k=Xn×DUD×k=

(9)

式中，Zn×k为用k维的数据表示原始D维数据。

Zn×k不仅降低了数据的冗余度，对提高用户分类速度有很大的作用。

3 用户分类

在台区电压与用户用电关系辨识中，不同用电等级的用户与台区电压具有不同的关联程度。假设有数据集X，把数据分为c类，对应就有c个类中心C1,C2,…,Cc。把每个样本j按照预设的类簇归类，得到用电等级分别为大、中、小3个等级的用户。根据皮尔逊相关系数的物理含义，对不同等级的用户分析其峰-谷-平期间对台区电压波动的影响，得出哪些用户在特定的用电期间与台区电压波动有较强的关联性。

3.1 模糊聚类分析

模糊聚类是在传统k均值硬聚类的基础上加上隶属度模糊概念的一种聚类分析方法。假设每个样本j属于某一类i存在隶属度uij的关系，由此构建FCM目标函数及其约束条件：

(10)

(11)

式中：m为一个隶属度的因子；n为所有样本个数。

式(11)为约束条件，说明一个样本属于所有类的隶属度之和恒为1。

3.2 模糊聚类中心

采用模糊聚类分析的方法，选取聚类中心个数c，把所有用户分为3类：大用户、中等用户及小用户。构建数据集的聚类中心：Ci={ci,1，ci,2,…,ci,k}(i=1,2,3)，其中ci,k为第i个聚类中心第k维的聚类中心特征值。

3.3 最优模糊聚类中心矩阵迭代计算

采用模糊聚类分析方法，通过迭代计算，确定模糊C-均值聚类矩阵的最优聚类中心，确定用户所属类簇。具体迭代步骤如下：

1)初始化：确定类别数C、隶属度因子m、迭代停止误差ε以及最大迭代次数(LOOP)。

2)初始化聚类中心P。

3)计算初始距离矩阵D。

4)按式(12)更新用户与聚类中心的隶属度。

(12)

式中，d(·)为样本点到样本中心的距离函数。若样本距离中心距离为0，隶属度设为1，即完全属于该中心，否则按照推导式子确定隶属度。

5)更新聚类中心。

(13)

6)重新计算距离矩阵，并计算目标函数值。

(14)

7)若达到最大迭代次数或者前后两次J的绝对差小于预设误差ε则结束，否则转步骤4。具体的模糊聚类迭代流程如图3所示。

图3 模糊聚类流程

4 实例仿真与分析

以广州某小区为实例，利用其配电系统用户用电历史数据，选取其所属台区某个变压器低压侧A相下91户在6月21日至6月27日间的历史用电有功数据，分辨率为15 min，共672个有功功率初值，相应地选取该变压器低压侧A相672个电压值。由于用电数据在采集过程中有缺值，利用插值法对空值进行估算补全。

4.1 数据特征分析

采用PCA对数据进行降维处理。经过多次数据仿真估算，验证了当采用63维PCA特征数据可以表达原始数据95%的特征贡献度，而且可以将聚类分析聚类结果偏差控制在1%以内。因此，选择把原始数据维度降为63维度，这样既可保持数据原始特征，又可以减少聚类整体计算时间。

维度选取为

(15)

式中：Sk,fron为前k个特征值组成的面积；Sall为所有特征值组成的总面积；ηk,ctb为前k个特征值特征贡献度。特征贡献度如图4所示。

图4 PCA的降维贡献度

4.2 用户的分类

采用插值法补全原始数据，共91户，672维特征值。采用模糊C-均值聚类结果如图5所示。由于用户之间存在用电行为相似度较高，其数据特征不明显，同一个用户在3个聚类中心隶属度比较时容易陷入某两个中心最优解，如图6所示。聚类迭代进行到第8代至第10代，目标函数在第8代陷入早熟、收敛，如图7所示。

图5 基于插值法的模糊聚类结果

图6 基于插值法的模糊聚类隶属度

图7 基于插值法的模糊聚类迭代次数

采用原始数据进行聚类的方法只能得到两类用户，几乎不能分辨出第3类用户。只有在用户数据量足够多才能分辨出第3类用户，但此时存在数据量冗余度高、计算量大、计算时间长等问题。

采用皮尔逊相关系数聚类方法，对用户用电与台区电压的关联程度进行聚类，能够区分出用户对于台区电压影响程度。

但是，皮尔逊相关系数仅仅反映的是某一户与台区的关联程度。由于数据具有高维特性，可能是某一些维度对此造成了较大的影响，并不能区分该用户等级，不能体现整体性，只能作为部分参考对象。皮尔逊相关系数仿真结果如图8至图9所示。

图8 基于皮尔逊法的模糊聚类结果

图9 基于皮尔逊法的模糊聚类迭代次数

考虑到数据维数较高、数据特征不突出容易陷入局部最优、聚类计算量大等原因，运用PCA法可以解决上述问题。采用PCA法可以提取原数据95%特征贡献度，用63维数据表示原始数据672维特征。

仿真结果说明，运用PCA法，迭代次数在35次左右，收敛时间一般可以控制在0.568 0～0.589 1 s。对比加权后从小到大排序，采用PCA聚类得到的用户等级，聚类偏差在4%左右，对应上面按照95%特征贡献度，负荷误差可接受范围整体误差在1%左右。PCA法仿真结果如图10至图12所示。

图10 基于PCA法的模糊聚类结果

图11 基于PCA法的模糊聚类隶属度

图12 基于PCA法的模糊聚类迭代次数

采用PCA法，确定大、中、小等级用户数目分别是28、33、30；相对误差率约为1%。而采用皮尔逊相关系数法，确定大、中、小等级用户的数目分别是33、15、43。

相对误差率计算式为

(16)

式中：ηre为聚类用户等级相对误差率；ncls为聚类类簇包含用户数；nset为实际应分类簇用户数；nz为总的用户数；ηpca为PCA特征贡献率。

表2为不同聚类方法的比较结果。从表2可见：1)采用基于插值法的模糊聚类，因用户之间数值相似度较高，发现某些粒子只能陷于某一个或者两个聚类中心之间，容易陷入早熟，聚类效果不好，小数据容易陷入早熟，大量数据聚类消耗时间长；2)采用基于皮尔逊相关系数的模糊聚类，聚类花费时间短，分类效果好，但是只能反映相关程度，体现某一个粒子与聚类中心的整体关联程度，不能体现各个时间点联系紧密程度，且对于用户等级的分类误差率较高，皮尔逊特征值聚类不适合用于用户等级分类，只适用于用户对于变压器低压侧电压影响度辨识；3)采用基于PCA法的模糊聚类，提取特征值聚类收敛时间短，分类效果好，相对误差率达1%，适合用于用户等级分类。

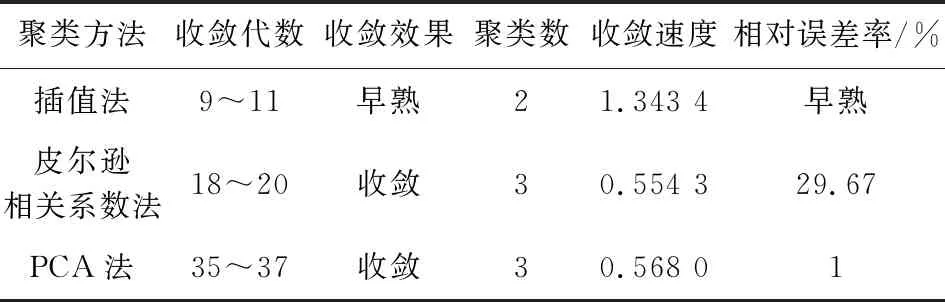
表2 不同聚类方法的比较

综上，在台区电压与用户用电关系辨识中，结合PCA特征值聚类法与皮尔逊相关系数，能找出既具有等级分化且有较高影响因子的用户，此类用户即是供电管理部门需要重点关注的对象。

4.3 用户用电行为分析

4.3.1 峰-谷-平荷期大用户用电行为分析

由用户聚类结果与皮尔逊相关系数，从大用户类簇中选取第85号、第86号用户，影响因子分别为-0.215 3和0.107 6。该用户的峰-谷-平负荷曲线如图13所示，第85号用户15:00 — 16:00处于用电低谷区间，此时变压器低压端电压基本保持在238 V以上；16:15以后用电功率逐渐到达峰值，变压器电压逐渐下降到235 V，该用户高峰区间一直持续到20:15，变压器低压侧电压保持235 V，电压波动范围3～4 V；22:15 — 00:00用电功率处于平荷区，此时变压器电压稳定在238 V。综合皮尔逊相关系数表与功率-电压仿真图，该用户的用电行为与变压器电压波动具有较强关系。大用户用电负荷曲线如图13所示。

图13 大用户在峰-谷-平期用电负荷特性

4.3.2 峰-谷-平荷期小用户用电行为分析

对于小用户，选取第26户为分析对象，皮尔逊相关系数为0.14且为小用户中相关系数最大的用户，对其进行关联性分析：结果显示该用户在17:15 —18:45处于用电低谷区，对比同时间段的第85号大用户用电功率正处于高峰，电压处于较低235 V；该用户在22:00 — 22:30处于用电高峰，但此区间变压器电压呈现上升趋势。综合皮尔逊系数及台户功率-电压仿真图，第26号小用户并不如第85号大用户与变压器电压波动具有较强的相关性，小用户用电负荷曲线如图14所示。

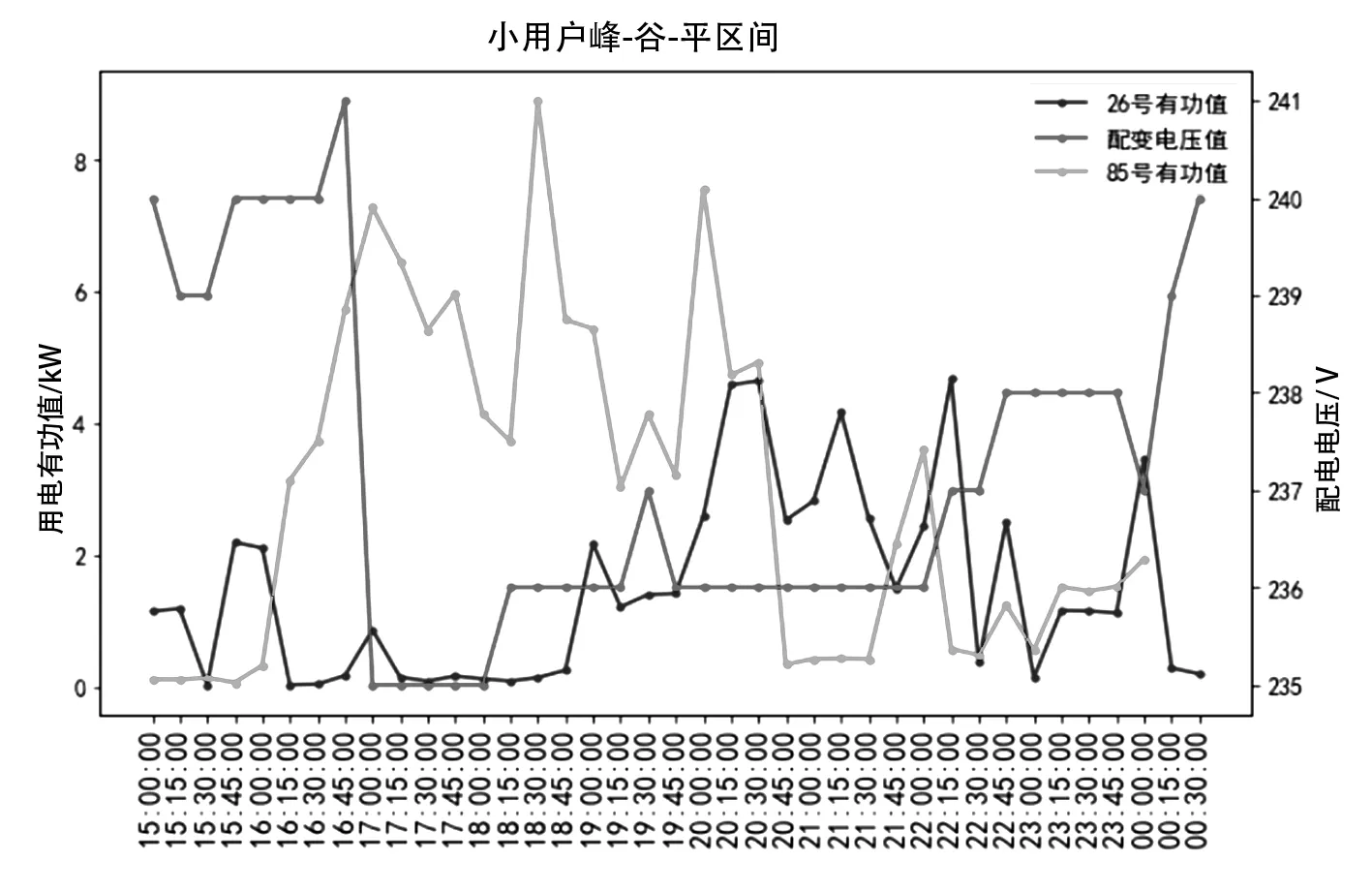
图14 小用户在峰-谷-平期用电负荷特性

在小用户类簇当中，依据皮尔逊相关系数选取用电行为相近的户号：5、7、18、26、27、37，这些都属于该台区下A相小用户。其皮尔逊相关系数保持在0.1左右，重新计算以上用户连成一片用电区域与变压器电压之间的皮尔逊系数为-0.203 2。由负荷曲线与电压曲线图15可知，在这一片用户中，15:00—16:00保持在用电低谷区，此时变压器电压保持240 V；18:00—18:45逐渐达到用电峰值，变压器电压同步下降到235 V；22:45—23:15为该片区域用电平荷期，变压器电压同时保持238 V。结合皮尔逊相关系数与该片区域峰-谷-平期有功功率、变压器电压的变化趋势，该区域用户用电行为与变压器电压波动具有较强的相关性。多用户用电负荷曲线如图15所示。