如何正确运用χ2检验——高维表资料优势比分析与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

为了分析来自病例对照研究设计的g×2×2表资料，需要完成以下4项任务：其一，检验各层2×2表资料的优势比是否满足齐性；其二，估计共同优势比的数值；其三，估计共同优势比的置信区间；其四，检验共同优势比是否等于1。本文将对后三项任务有关内容进行介绍。

1 高维表资料共同优势比分析的基本概念

1.1 高维表g×2×2表的表达模式

设高维表g×2×2表的表达模式如下，见表1。

表1 病例对照研究设计下g×2×2表的第h层2×2表资料的表达模式

1.2 高维表资料共同优势比的含义

在分析“病例对照研究设计”的二维表资料时，可以很方便地依据公式“OR=ad/bc”计算出优势比OR的数值。然而，对于“g×2×2表资料”，却无法直接计算出OR的数值。从概念上来说，似乎可以采取某种举措，将“g×2×2表资料”降维或压缩成一个“2×2表资料”。但事实上，这种理想的“2×2表资料”是无法直接呈现出来的。于是，统计学家通过统计学方法来体现出各层“2×2表资料”之间的“微小差别”，这就是求出各层“2×2表资料”的“权重系数wh”。通过它将各层“2×2表资料”进行加权平均，从而间接获得合并后的优势比OR的数值。在SAS/STAT的FREQ过程中，将其称为“common odds ratios”［1］，常译成“共同或普通或合并优势比”。

1.3 估计共同优势比的前提条件

基于“g×2×2表资料”计算共同优势比的前提条件是高维表资料应满足齐性，针对“优势比”，检验高维表资料是否满足齐性的检验方法有5种，分别是“Breslow-Day检验”“Breslow-Day-Tarone检验”“Q检验”“I2度量统计量及其不确定性限值”和“Zelen's精确检验”。

1.4 估计共同优势比及其置信区间的方法概述

SAS/STAT中的FREQ过程［1］采用3种方法估计共同优势比及置信区间，分别是：①校正的计算方法，Mantel-Haenszel估计法；②校正的计算方法，logit估计法；③基于条件分布的精确法。

2 高维表资料优势比分析及SAS实现

2.1 高维表资料优势比分析的具体算法

2.1.1 高维表资料优势比分析的具体内容

高维表资料优势比分析的具体内容包括以下4项［1］：其一，检验资料是否满足齐性要求；其二，估计共同优势比；其三，估计共同优势比的置信区间；其四，检验共同优势比是否等于1。

2.1.2 高维表资料共同优势比的点估计及置信区间估计

2.1.2.1 Mantel-Haenszel估计量

基于Mantel-Haenszel估计量（简称MH估计量）估计高维表资料共同优势比，见式（1）：

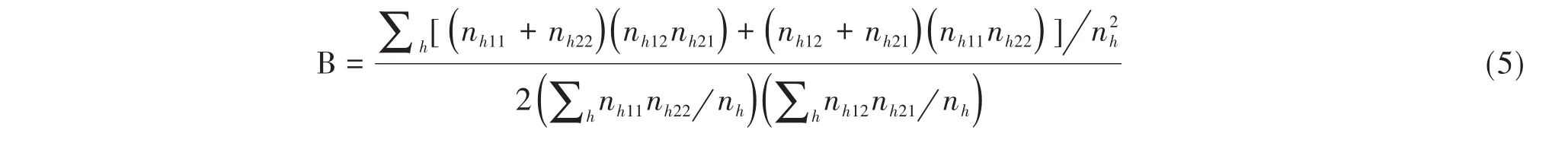
注意：当nh较小时，MH估计量不如logit估计量敏感。

2.1.2.2 Logit估计量

Woolf于1955年提出了logit估计量［1］，见下式：

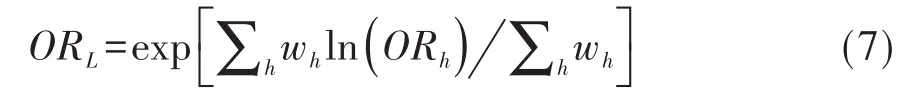
式（7）中，ORh是第h层的优势比，其100（1-α）%置信区间见下式：

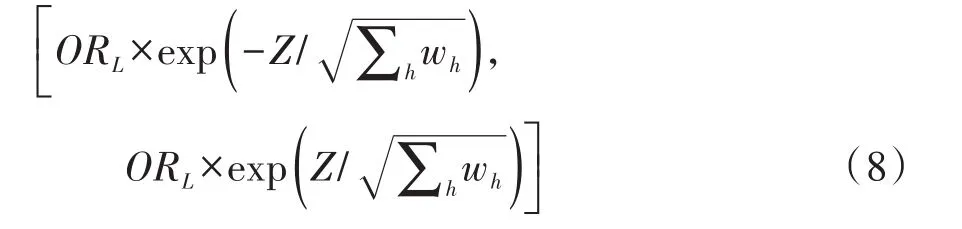
在式（7）和式（8）中，wh是第h层的权重系数，其定义见下式：

在式（9）中，Var［ln（ORh）］的定义见下式：

当第h层的表格中出现0频数时，在计算ORh和wh之前，需要给该层的所有格加上 0.5［1］。

2.1.3 高维表资料共同优势比的精确置信区间估计

假定所有各层2×2表的优势比是一个常数。精确置信限的构造原理：在各层2×2表的边际总数固定的条件下，基于S=∑hnh11的分布来构造精确置信限。精确置信区间的精度：Agresti于1992年指出，由于拟解决的问题是一个离散问题，所以，所构造的精确置信区间的“置信水平”不会恰好等于100（1-α）%，但至少是100（1-α）%。因此，所求得的置信限是保守的［1］。精确置信限算法的来源：SAS/STAT中的FREQ过程计算共同优势比的置信限是依据Vollset、Hirji和Elashoff于1991年提出的算法，还可参考Mehta、Patel和Gray于1985年发表的有关文献［1］。

算法的详细描述：在第h层2×2表的边际总数固定的条件下，让随机变量Sh代表第h层2×2表中（1，1）网格内的频数。给定行合计nh1·、nh2·，列合计nh·1、nh·2，Sh的下限与上限是 lh、uh，则它们的计算公式分别见式（11）和式（12）：

让s0代表所有q张表第（1，1）格上频数之和。通过迭代计算方法求解下列两个方程中的共同优势比置信限的下限值与上限值，φ1与 φ2，见式（16）、式（17）：

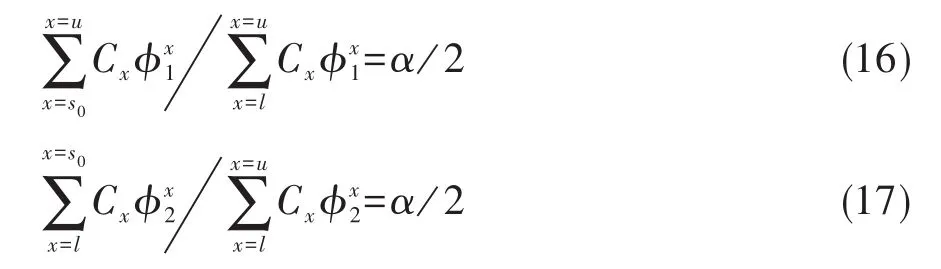
当观测结果的和s0等于下界l时，SAS/STAT中的FREQ过程就将置信限的下限设置为0，并基于显著性水平α来决定置信限的上限值；同理，当观测结果的和s0等于上界u时，SAS/STAT中的FREQ过程就将置信限的上限设置为∞，并基于显著性水平α来决定置信限的下限值。

2.1.4 高维表资料共同优势比是否等于1的精确检验

在运用SAS/STAT中的FREQ过程时，若在exact语句中使用了选项“COMOR”，该过程可以计算精确检验。设φ=1，在无效假设成立的条件下，S的条件分布变成如下形式：

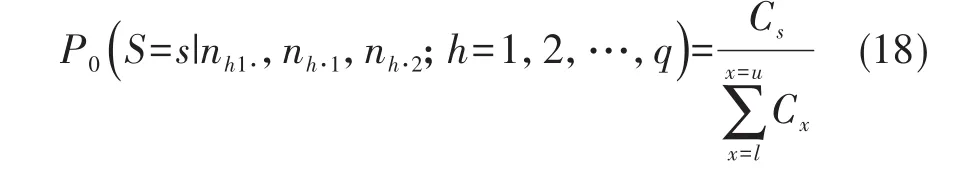
在无效假设成立且满足分层2×2表的边际固定的条件下，这个精确检验的点概率就是观测和s0出现的概率，这个概率可以用P0（s0）表示。在无效假设成立的条件下，S的期望值由下式定义：

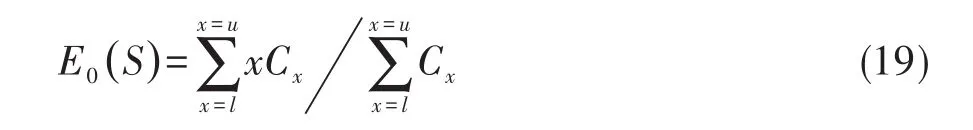
单侧精确概率P值（记为P1）可从条件分布P0（S≥s0）或P0（S≤s0）计算得到，取决于观测结果的和s0大于还是小于E0（S），分别见下式：

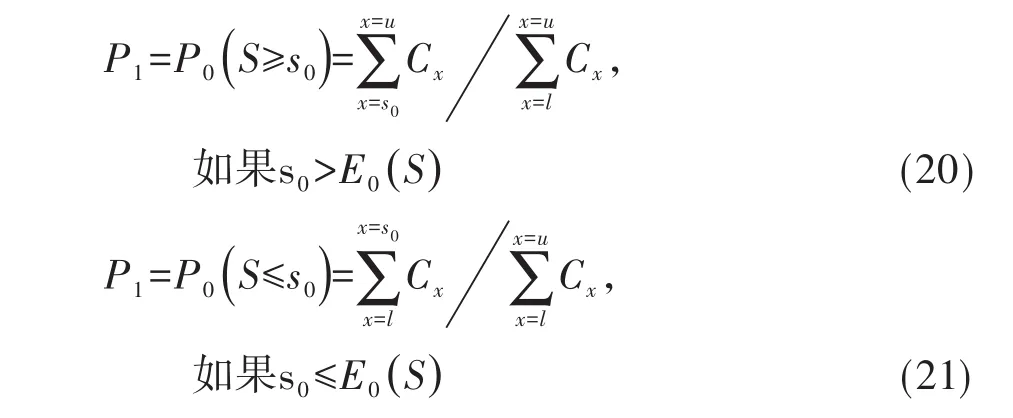
基于下面3种定义，可分别计算出双侧精确概率P值（记为P2）。

定义1：双侧概率为单侧概率的2倍。若该值超过1，将其设置为1。见下式：

定义2：双侧概率为所有小于等于观测结果的和s0的点概率的概率之和，求和范围是s的所有可能取值，即l≤s≤u，公式如下：

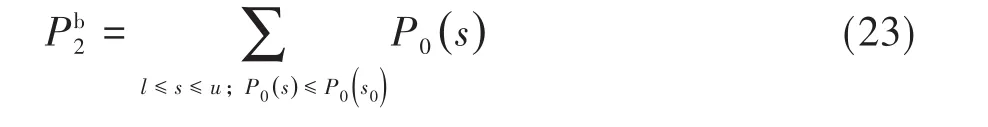
定义3：双侧概率为单侧P值与分布的对侧尾端（与期望值等距）相对应的面积之和，计算公式如下：

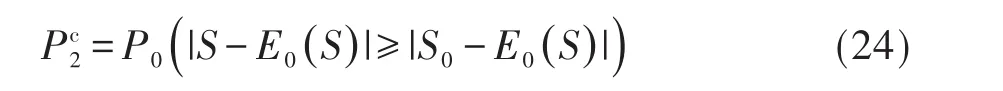
2.2 高维表资料优势比分析的SAS实现

2.2.1 问题与数据

【例1】文献［2］提供了如下资料，试对5项研究的共同优势比进行分析。见表2。

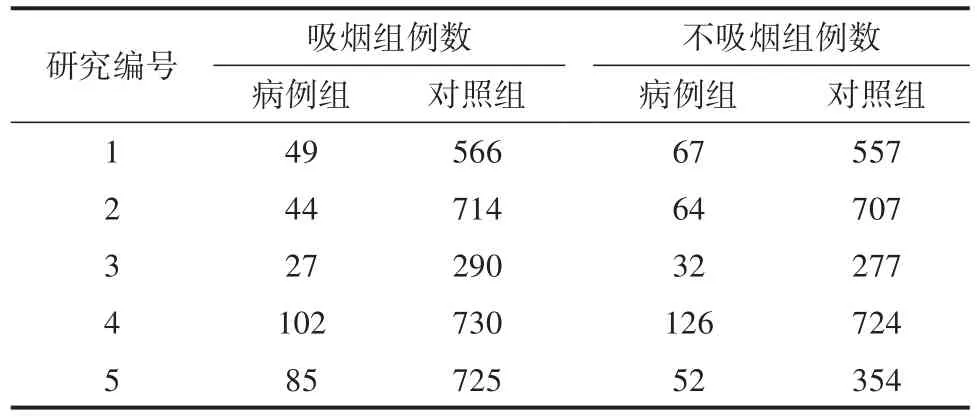
表2 吸烟与肝细胞癌关系的5项病例对照研究结果

【例2】文献［2］提供了如下资料，试对6项研究的共同优势比进行分析。见表3。

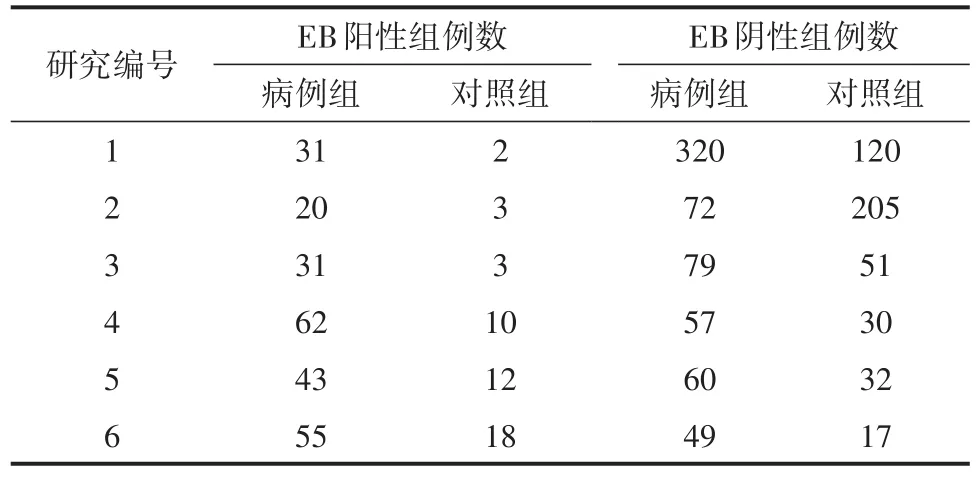
表3 鼻咽癌与EB病毒感染关系的6项病例对照研究结果

2.2.2 共同优势比分析的SAS实现

【例3】沿用例1中的“问题与数据”，试对5项研究的共同优势比进行分析。

【分析与解答】设所需要的SAS程序如下：

【程序说明】“exact语句”中的选项“eqor”要求对各层优势比OR是否满足齐性进行Zelen's精确检验；选项“comor”要求对共同优势比进行精确检验。

【SAS输出结果及解释】

以上输出的是“普通优比和相对风险”的计算结果，其中，“普通优比”也叫做“共同优比”。实际上，就是基于“Mantel-Haenszel法”和“logit法”计算出来的校正“共同优比”的估计值及其95%置信区间。在本例中，因95%置信区间不包含1，说明共同优比与1之间的差别具有统计学意义。

此处原本是各层2×2表优比齐性检验结果，结果显示，此资料满足齐性（这部分计算结果在本期“科研方法专题”的《如何正确运用χ2检验——高维表资料齐性检验与SAS实现》中已经呈现了，限于篇幅，此处从略）。关于共同优比的估计和置信区间的计算，直接利用前面的“校正计算结果”即可。但在SAS/STAT的FREQ过程中，还可采取精确计算法，以获得更加可靠的计算结果如下：

以上输出的是共同优比的点估计值及其精确置信区间，因95%置信区间不包含1，说明共同优比与1之间的差别具有统计学意义。

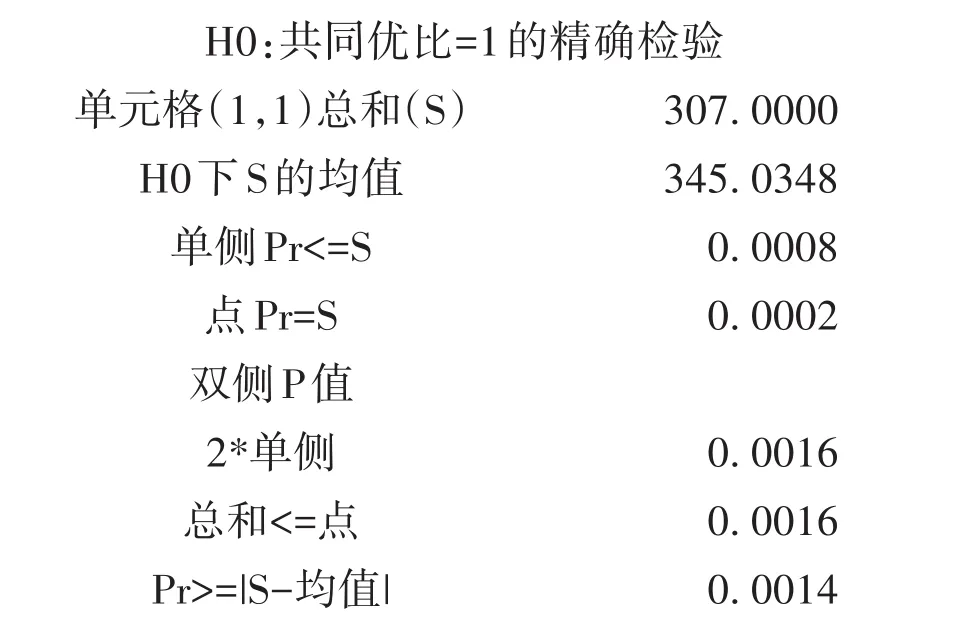
以上输出的是关于共同优比是否等于1的精确检验结果。其中，“S=307”是高维表资料中各层2×2表中第（1，1）格上频数之和；“SH0=345.0348”是 H0（即“共同优比=1”）成立条件下推导出各层2×2表中第（1，1）格上频数之和；点概率P（S=307）=0.0002，与其对应的单侧概率为0.0008；与其对应的双侧概率P2有3个，分别基于不同的定义而算得，即基于定义1，得=0.0016；基于定义2，得=0.0016；基于定义3，得=0.0014。

【结论】无论是基于单侧检验还是双侧检验，所得P值都小于0.01，说明应拒绝H0（即“共同优比=1”），接受H1（即“共同优比≠1”）。因优比的点估计值为0.7836（MH法），说明吸烟组的优势（odd值）小于不吸烟组的优势（odd值）；更明确的专业结论是：吸烟者患肝细胞癌的风险小于不吸烟者患肝细胞癌的风险（注意：这个结论与临床专业知识不相符，具体原因可能是原始资料中存在过失误差，有待进一步核实）。

【例4】沿用例2中的“问题与数据”，试对6项研究的共同优势比进行分析。

【分析与解答】设所需要的SAS程序如下：

【SAS输出结果及解释】

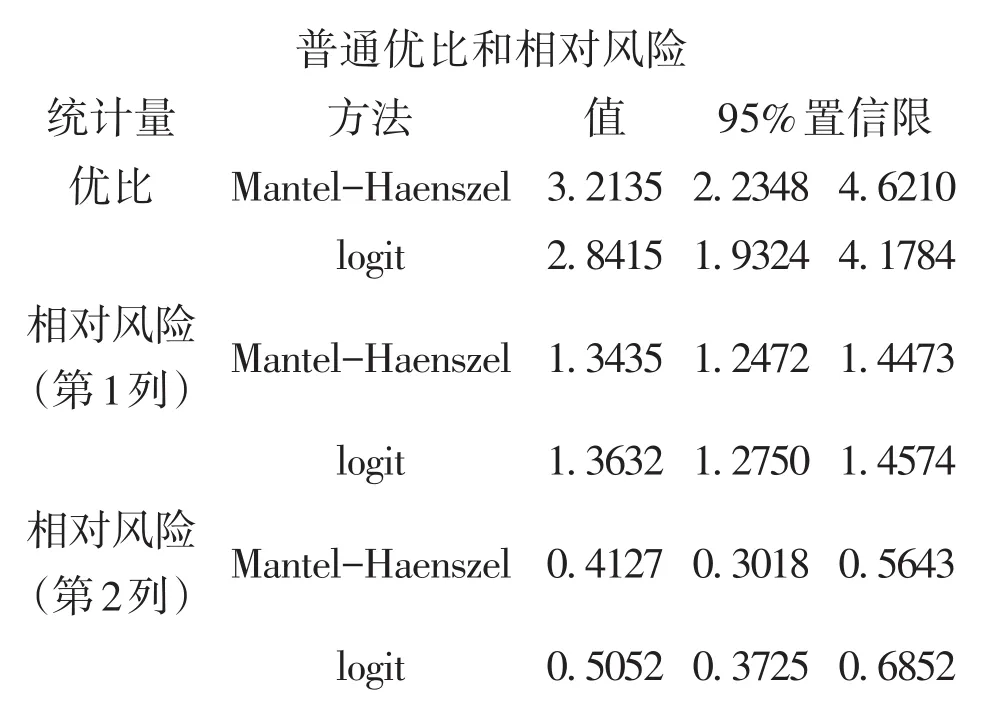
以上输出的是“普通优比和相对风险”的计算结果，其中，“普通优比”也叫做“共同优比”。实际上，就是基于“Mantel-Haenszel法”和“logit法”计算出来的校正“共同优比”的估计值及其95%置信区间。在本例中，因95%置信区间不包含1，说明共同优比与1之间的差别具有统计学意义。

此处原本是各层2×2表资料优比齐性检验结果，结果显示，此资料不满足齐性（这部分计算结果在本期“科研方法专题”的《如何正确运用χ2检验——高维表资料齐性检验与SAS实现》中已经呈现了，限于篇幅，此处从略）。关于共同优比的估计和置信区间的估计，通常的做法是基于随机效应模型推导出的公式进行计算。而在SAS/STAT的FREQ过程中，采取精确计算法，输出结果如下：

以上输出的是共同优比的点估计值及其精确置信区间，因95%置信区间不包含1，说明共同优比与1之间的差别具有统计学意义。

以上输出的是关于共同优比是否等于1的精确检验结果。其中，“S=242”是高维表资料中各层2×2表中第（1，1）格上频数之和；“SH0=201.3895”是 H0（即“共同优比=1”）成立条件下推导出各层2×2表中第（1，1）格上频数之和；点概率P（S=242）＜0.0001，与其对应的单侧概率＜0.0001；与其对应的双侧概率P2有3个，分别基于不同的定义而算得，即基于定义1，得＜0.0001；基于定义2，得＜0.0001；基于定义3，得＜0.0001。

【结论】无论是基于单侧检验还是双侧检验，所得P值都小于0.0001，说明应拒绝H0（即“共同优比=1”），接受H1（即“共同优比≠1”）。因优比的点估计值为3.2135（MH法），说明EB阳性组的优势（odd值）大于EB阴性组的优势（odd值）；更明确的专业结论是：EB阳性者患鼻咽癌的风险大于EB阴性者患鼻咽癌的风险。

3 讨论与小结

3.1 讨论

欲基于g×2×2表资料求共同优势比，需要先检验资料是否满足齐性要求，即检验各层2×2表资料所对应的优势比是否相等。常规的做法［2-8］如下：若资料满足齐性要求，可基于固定效应模型推导出的公式估计优势比及其置信区间；若资料不满足齐性要求，可基于随机效应模型推导出的公式估计优势比及其置信区间。然而，在SAS/STAT的FREQ过程中，若资料满足齐性要求，可通过CMH χ2检验方法给出校正的计算结果，包括“校正的共同优势比的点估计值”及其“校正的95%置信区间”；若资料不满足齐性要求，可通过各层2×2表中（1，1）网格内的频数的条件分布来构造计算公式，可求得“共同优势比的精确点估计值”“精确95%置信区间”以及“共同优势比是否等于1”的精确单侧概率和精确双侧概率。

3.2 小结

本文对g×2×2表资料进行了优势比分析，其全部内容包括“各层2×2表资料齐性检验”“共同优势比的点估计和置信区间估计”和“共同优势比是否等于1的假设检验”。从计算的角度来看，内容涉及“校正算法”和“精确算法”。通过两个实例，演示了基于SAS软件实现优势比分析的内容，并对结果进行了解释，做出了统计和专业结论。