如何正确运用χ2检验——高维表资料统计分析方法概述
2021-07-20胡纯严胡良平
胡纯严 ,胡良平 ,2*
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu927@163.com)
在医学资料中,结果变量为定性变量的情形很常见。最常见的有如下3种情形:①结果变量为二值变量,例如“死亡与存活”“治愈与未治愈”和“复发与未复发”;②结果变量为多值有序变量,例如“治愈、显效、好转、无效、死亡”和“优、良、中、差”;③结果变量为多值名义变量,例如某种基因的类型为“AA、AB、BB”,某种疾病的类型为“慢性、亚急性、急性”。当仅考察一个原因变量时,收集到的资料常被整理成二维列联表(简称为二维表)形式[1-2];当考察的原因变量的个数≥2时,收集到的资料常被整理成高维列联表(简称为高维表)形式(参见本文中的表1~表4)。分析高维表资料的统计方法主要有两大类,第一类为广义差异性分析,第二类为回归分析。本文将概括介绍高维表资料的种类和有关实例及其相应的统计分析方法。
1 高维表资料的种类及实例
1.1 二值结果变量的高维表资料及其实例
【例1】文献[3]呈现了如下资料,为研究阿司匹林对心血管事件发生的预防作用,研究者收集了满足要求的7项临床随机对照试验资料,见表1。
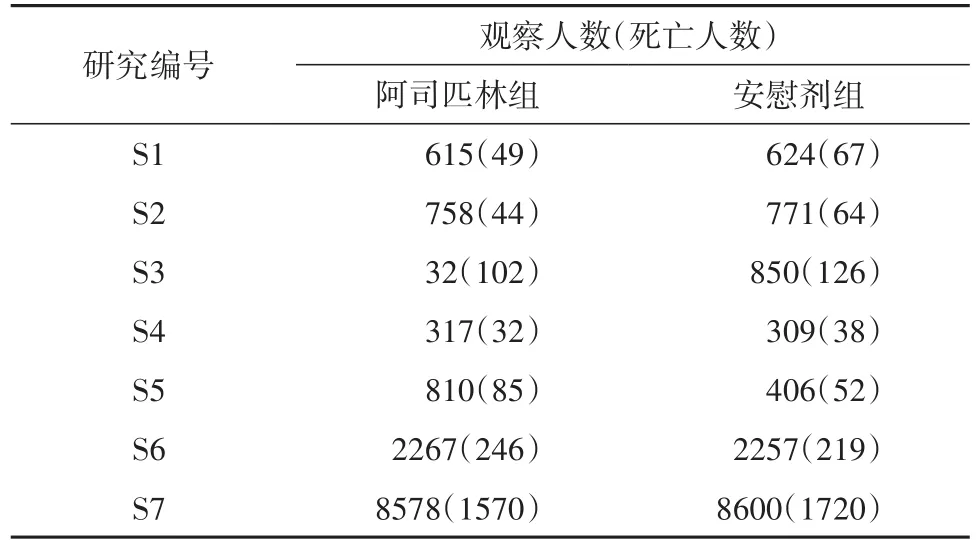
表1 阿司匹林预防心肌梗死后死亡的7项随机对照试验研究结果
1.2 多值有序结果变量的高维表资料及其实例
【例2】假设某研究者为了研究“甲、乙两种治疗方法对不同病程和不同病情的某病患者的治疗效果”,收集到如下资料,见表2。
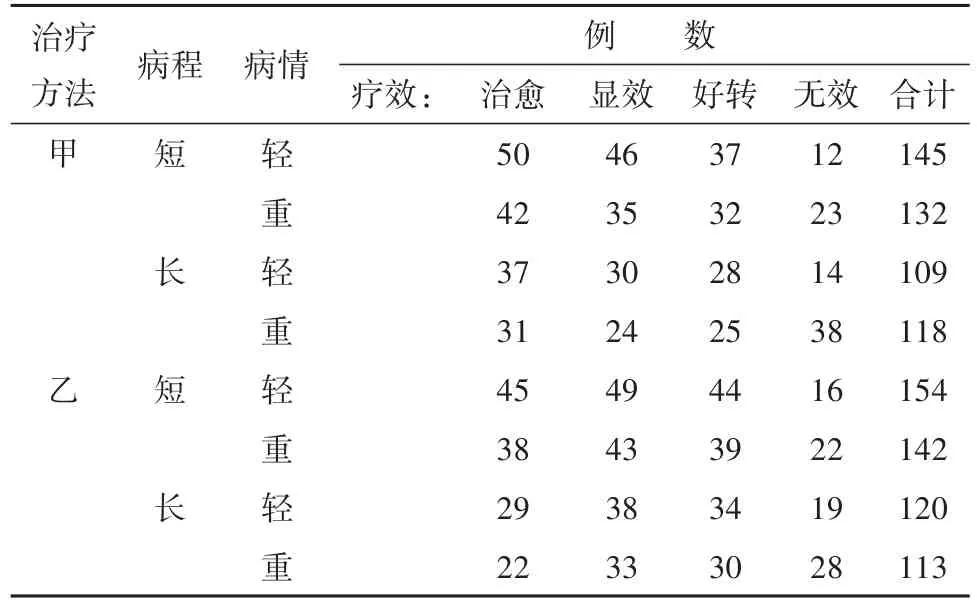
表2 甲、乙两种治疗方法对不同病程和不同病情的患者治疗效果
1.3 多值名义结果变量的高维表资料及其实例
【例3】假设某研究者为了研究“细胞分化程度和细胞染色与恶性肿瘤组织类型之间的关系”,收集到如下资料,见表3。
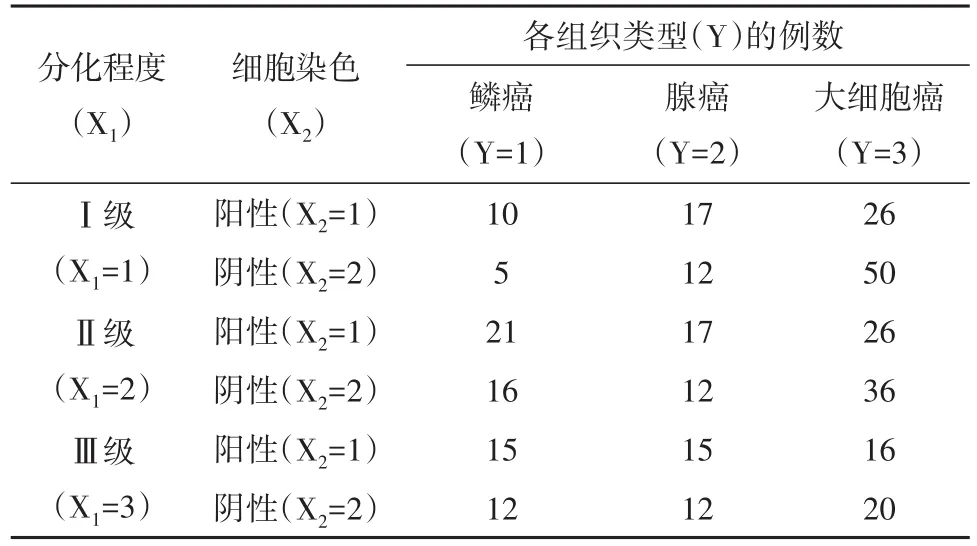
表3 细胞分化程度和细胞染色与恶性肿瘤组织类型之间的关系
1.4 特殊的高维表资料及实例(简称为“人-时间数据”)
【例4】某研究探讨乙型肝炎病毒(HBV)感染对健康的影响,在原发性肝癌高发区江苏省海门市进行前瞻性队列研究,对研究对象进行流行病学调查,调查结果见表4。
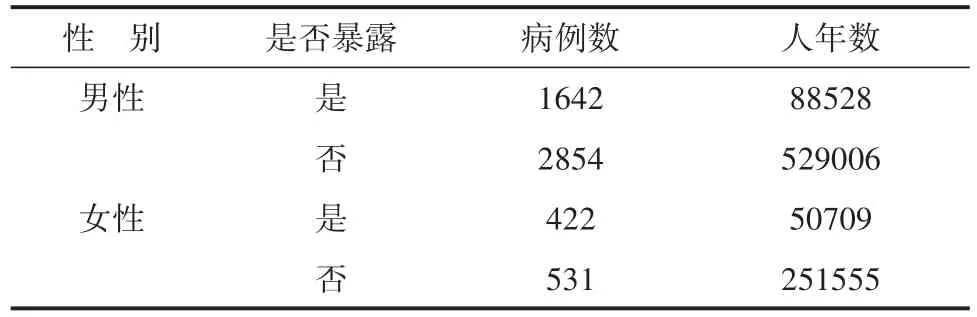
表4 1993年-2003年调查人群的死亡情况
【说明】之所以说表4资料具有特殊性,是因为表中各行上除了提供“病例数”之外,还提供了“人年数(即各组中全部受试者所经历的年数之合计值)”,而不是“阴性例数”,也不是“总例数”。分析表4资料,需要对“人年数”进行特殊处理,因篇幅所限,本文不予赘述,可参阅文献[4]。
2 分析高维表资料的两类统计分析方法简介
2.1 两类统计分析方法概述
高维表资料的统计分析方法主要有两大类,第一类为广义差异性分析,内容包括“加权χ2检验”“CMHχ2检验”和“Meta分析”;第二类为回归分析,内容包括“对数线性回归模型分析”“Logistic回归模型分析”“Probit回归模型分析”和“离散选择模型分析”。这两类分析方法的区别在于:第一类方法是将多因素降维成单因素问题,属于“基于分层后单个检验统计量的构造及实现”,其结果比较单一;而第二类方法是直接构建定性因变量依赖多因素及其交互作用项变化的回归模型,并采用多种复杂的统计分析方法估计和检验模型中的参数,其结果比较丰富,而且可以更加全面地挖掘资料所蕴含的信息。
2.2 广义差异性分析方法
2.2.1 加权χ2检验
在分析二维表资料时,为了检验表中两属性变量之间是否独立,可采用Pearson'sχ2检验、校正的Pearson'sχ2检验和似然比χ2检验。然而,在分析高维表资料时,以上方法均不能直接使用,需要按一个定性变量的各水平或多个定性变量的水平组合进行分层,当各层都是“2×2表资料”时,就可按特定的公式求出各层的权重系数,并进行“加权合并计算”,这就是“加权χ2检验[5]”。
2.2.2 CMHχ2检验
在分析二维表资料时,CMHχ2检验实际上包含了三种检验,即“两属性变量之间的独立性检验(H1:一般关联)”“两有序变量之间的相关性检验(H1:非零相关)”和“定性原因变量各水平下定性结果变量的平均秩之间的差异性大小的秩和检验(H1:行评分均值差异)”;而在分析高维表资料时,首先要对资料进行分层,再进行“合并计算”。CMHχ2检验的结果与前面提及的三种检验结果类似,具体地说,若分层后,各层都是“2×2表资料”时,三种检验结果是完全相同的;若分层后,各层都不是“2×2表资料”时,三种检验结果中,“H1:非零相关”与“H1:行评分均值差异”的检验结果相同,而“H1:一般关联”的检验结果与前两种的检验结果是不同的[6]。
2.2.3 Meta分析
对三维表资料进行Meta分析的任务有以下4项:①弄清定性资料来自队列研究设计还是病例对照研究设计。②选定拟分析的效应指标,例如,队列研究设计时,其效应指标有“相对危险度(RR)”或“危险率差(RD)”;病例对照研究设计时,其效应指标有“优势比(OR)”。③检验各层(即各研究项目)的“2×2表资料”之间是否满足齐性。具体地说,对于队列研究设计资料而言,就是检验各层“相对危险度(RR)”之间是否相等或各层“危险率差(RD)”之间是否相等;而对于病例对照研究设计资料而言,就是检验各层“优势比(OR)”之间是否相等。④计算“合并后资料”的“效应指标(RR或RD或OR)”的估计值及其置信区间。在进行前述两步计算时,都必须依据“齐性检验”结果来选择具体方法。
传统算法体系的解决方案:在常规的统计学教科书[3,7-8]和用于 Meta分析的统计软件(例如 Review Manager软件[9])中,都采取如下策略:第一步,针对不同的“效应指标[(RR或lnRR)或RD或(OR或lnOR)]”构造不同的检验统计量Q,检验各层2×2表资料是否满足齐性要求;第二步,若“分层2×2表资料”满足齐性要求,则采取基于“固定效应模型”导出的公式进行特定效应指标估计和置信区间估计,若“分层2×2表资料”不满足齐性,则采取基于“随机效应模型”导出的公式进行特定效应指标估计和置信区间估计。
SAS算法体系的解决方案:在SAS/STAT的FREQ过程中[6],只出现了关于“各层优势比(OR)”齐性检验的方法,没有给出关于“相对危险度(RR或lnRR)”或“危险率差(RD)”齐性检验的方法。优势比齐性检验的具体方法有以下四种[6]:“Breslow-Day检验”“Q检验”“计算I2度量统计量及其95%置信区间”和“Zelen’s精确检验”。在SAS/STAT的FREQ过程中[6],没有明确提及“固定效应模型”与“随机效应模型”的概念,只要在“tables语句”中增加了选项“CMH”,于是,在SAS输出结果中,就会输出“普通优比和相对风险”(或称为“共同优比和相对风险”)的计算结果,具体内容如下所示:
在上面输出的结果中,第1列为“统计量”,有“优比”和“相对风险”两种,相对风险又分为两种计算结果,分别基于“分层2×2表”的“第1列”和“第2列”计算所得。若研究者将自己所关心的结局(例如:死亡)放置在表中第1列上,就看“相对风险(第1列)”所在的行;否则,就看“相对风险(第2列)”所在的行。无论是哪一种统计量的估计值和置信区间,SAS都基于两种方法(即“校正的Mantel-Haenszel法”与“校正的logit法”)进行计算并输出相应的结果。通过比较发现,它们可以被视为基于“固定效应模型”计算的“估计值及95%置信区间”。
下面输出结果中的“精确置信限”可以被视为基于“随机效应模型”计算的“共同优比估计值及95%置信区间”。

值得一提的是,在SAS/STAT的FREQ过程中,尚未给出与“共同相对危险度(即按分层因素进行合并计算的相对危险度)”对应的精确检验方法,也就是说,当对队列研究设计高维表资料进行Meta分析时,若“分层2×2表”资料不满足齐性要求时,需要基于随机效应模型导出的公式并借助SAS语言编程实现完整的计算[10]。
在使用SAS/STAT的FREQ过程中,只要在“tables语句”中增加了选项“commonriskdiff(test=mh cl=(k mh mr score newcombe newcombemr))”,于是,SAS输出结果就会呈现基于6种算法得到的“共同危险率差(RD)”的估计值及95%置信区间:
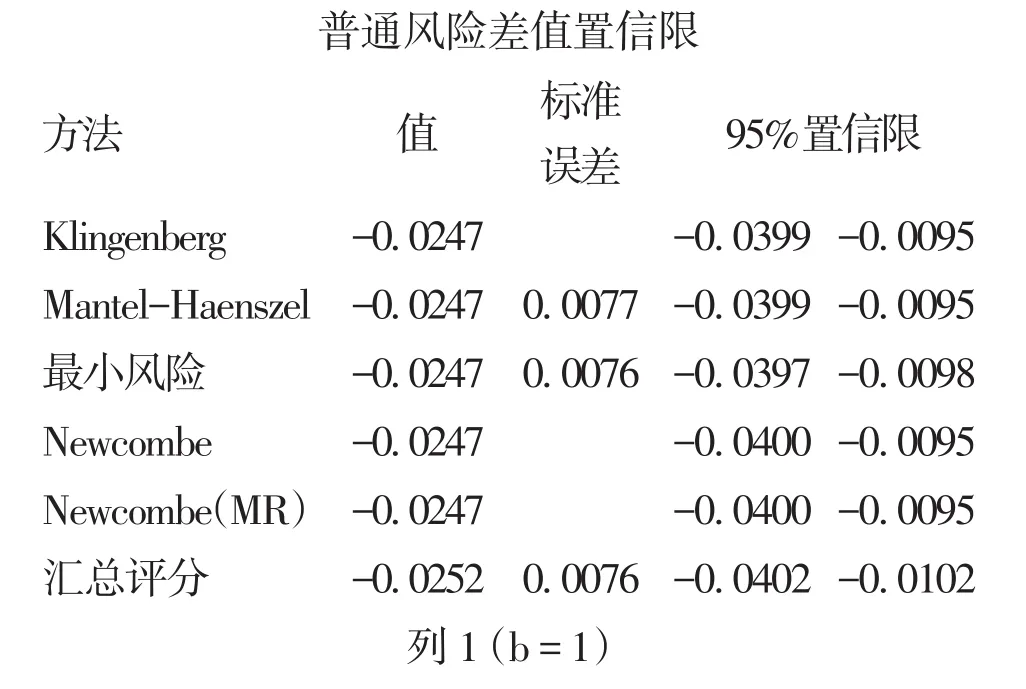
在上面的输出结果中,第1列是6种计算方法的名称,第2列为普通风险率差(RD)的估计值,最后2列为其95%置信区间的下限值与上限值。其中,最后一行上的“汇总评分法”也叫做“General variance-based 法”[7]。在这 6 种方法中,哪些是与“固定效应模型”对应的方法、哪些是与“随机效应模型”对应的方法,有待深入研究。
2.3 回归分析
2.3.1 对数线性回归模型
对数线性回归模型不仅可以解决χ2检验所能解决的变量间是否存在关联的问题,还可以解决χ2检验难以分析的多个变量间交互效应的问题。其分析过程是:先构建列联表中各网格中频数的对数(设为因变量)与多个分类变量(视为自变量)间关系的模型,然后用一定的统计方法(常用加权最小二乘方法和最大似然方法估计模型中的参数,并使用迭代法进行计算,如Newton-Raphson迭代法)以实际频数拟合模型、估计模型中的参数,并进行参数的假设检验。
2.3.2 Logistic回归模型
依据定性结果变量的不同类型,Logistic回归模型有3种,即二值结果变量的一般多重Logistic回归模型(包括配对设计资料和非配对设计资料两种情形)、多值有序结果变量的累计多重Logistic回归模型和多值名义结果变量的扩展(或称为多项)多重Logistic回归模型。在前述的几种情形下,依据资料的实际情况,还可以将它们分别扩展成为“带随机效应的多重 Logistic回归模型”[6]和/或“多水平多重Logistic回归模型”[11]。
2.3.3 Probit回归模型
Logistic回归模型与Probit回归模型都是用于分析定性(二值或多值的)响应变量与自变量之间的关系。它们之间最大区别在于:Probit回归分析中响应变量不再是二值变量,而是介于0~1之间的百分比变量。Probit回归分析中采用的关联函数为Probit函数,响应变量取值为1的概率如式(1)所示:
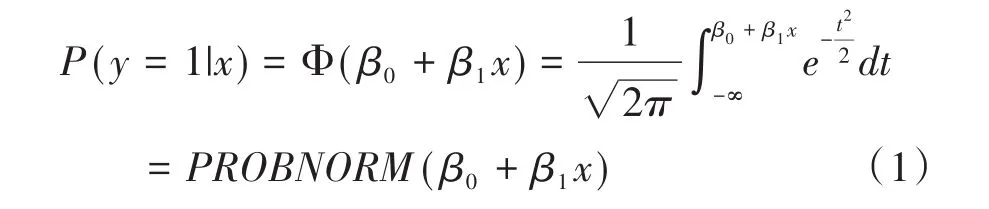
这个函数实际上就是标准正态分布曲线下分位数函数u=PROBIT(P)的反函数。式(1)中的β0+β1x就相当于这里的u。在医学研究中,此回归模型常用于估计药物或毒物的半数致死量[6]。
2.3.4 离散选择模型
统计学家在“效用最大化”的假设之下推导出离散选择模型。依据结果变量的表现形式,离散选择模型可分为以下两类。
第一类,当结果变量为有序变量(也被称为“偏好评分值”)时,此时的离散选择模型就是“结合分析中的回归模型”[10],见式(2):

在式(2)中,Y表示某种属性组合下被评对象的总效用,即轮廓的总效用。a为截距,v为属性变量各水平的分值效用,x为取值为0或1的哑变量,当它代表的属性水平出现,则x=1,否则x=0。
若模型中属性水平的分值效用的差值(最大效用与最小效用之差)越大,则该属性的相对重要性越高。一般用百分比的形式来描述各属性的重要性,见式(3):
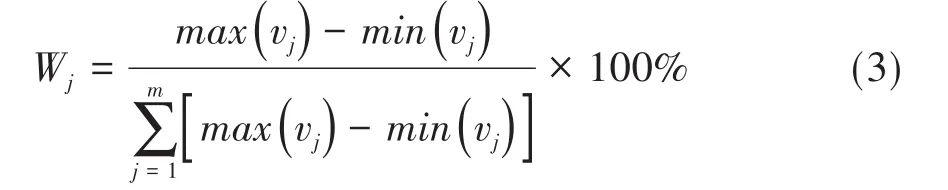
在式(3)中,m表示属性个数,Wj表示第j个属性的相对重要性,max(vj)和min(vj)分别表示第j个属性各水平中最大和最小的分值效用。
第二类,当结果变量为多选一(即从多项被选项目中选择一项,选中的项标记为1,其他未被选中的项一律标记为0)时,此时的离散选择模型(可进一步划分为“Logit模型”“Nested logit模型”和“Probit模型”)比较复杂[6],限于篇幅,不予赘述。
以上两类模型的适用场合如下:一类物品是否被顾客所青睐,取决于其自身多个属性变量的水平组合以及顾客自身的条件和偏好。例如,假设考虑小轿车的三个属性:车身(分为长、短)、耗油量(分为多、少)、价格(分为高、低),总共有2×2×2=8种型号的小轿车可供顾客选择。让某位顾客来挑选时,他或她有两种表达意愿的方式:其一,依次给这8种型号的小轿车打一个“分值(1~8分)”,分值越大,代表顾客越喜欢。此时,可选择前述提及的第一类离散选择模型;其二,仅从这8种型号的小轿车中选择一种,但参与选择的顾客人数至少应大于8,此时,可选择前述提及的第二类离散选择模型。
3 讨论与小结
3.1 讨论
处理高维表资料时,人们常会犯以下两种错误。
其一,将高维表资料简单地压缩成二维表资料,并直接对其进行统计分析,这样做很容易得出错误的结论。例如,采用CMH χ2检验分析一个关于“A、B两个诊所护理量多和护理量少所对应的婴儿死亡率的资料[12]”,所得结果如下:共同相对危险度为RR=1.1078,其95%置信区间为[0.3996,3.0707](Mantel-Haenszel法)、[0.3980,3.0662](logit法)。因置信区间包含1,说明护理量少与护理量多的婴儿死亡率接近相等;若对该资料中的A、B两个诊所进行简单合并,得到的四格表资料如下:

用CMH χ2检验分析上述简单合并后的四格表资料,得到的结果如下:
相对危险度为RR=2.7311,其95%置信区间为[1.1100,6.7198](Mantel-Haenszel法)、[1.1100,6.7198](logit法)。因置信区间不包含1,说明护理量少与护理量多的婴儿死亡率之间的差别具有统计学意义,前者的死亡率为5.35%、后者的死亡率为1.90%。显然,两个死亡率之间的差距被人为地夸大了。究其原因,不难发现:诊所A与诊所B的四格表资料之间不满足齐性,而且诊所B中“护理量多”的人数(25人)比诊所A中“护理量多”的人数(297人)少了很多。以致于简单合并后的资料中,原本死亡率高(8.00%)的诊所B中“护理量多”的那一行数据在合计中的“贡献或权重”很小,从而导致“护理量多”的合计栏中婴儿死亡率“下降”(这可能是一种假象)了很多。
其二,采用回归模型(对数线性模型除外)分析高维表资料时,人们常忽略因素之间的交互作用项。在使用Logistic回归模型和Probit回归模型时,使用者很少会把因素之间的交互作用项纳入回归模型中,因为统计学教科书中几乎都忽视了这一点。事实上,在有些实际问题中,因素之间的交互作用是不可忽视的,不将其纳于回归模型,可能会降低回归模型对资料的拟合效果。有时,可能会得出不符合实际的结论。
3.2 小结
本文以高维表形式呈现了三种常见的和一种特殊的多因素定性资料及实例,即“二值结果变量的高维表资料及其实例”“多值有序结果变量的高维表资料及其实例”“多值名义结果变量的高维表资料及其实例”和“人-时间数据及实例”;概括介绍了分析高维表资料的两类统计分析方法,即“广义差异性分析简介”和“回归分析简介”;最后,还讨论了处理高维表资料时常犯的两类错误,即“将高维表资料简单地压缩成二维表资料”和“基于回归模型分析时常忽略因素之间的交互作用项”。
