合成部队电子对抗能力灰色关联评估方法
2021-07-20范纪松董惠勤
范纪松,任 辉,董惠勤
(1.陆军工程大学训练基地,江苏 徐州 221004;2.空军勤务学院,江苏 徐州 221000)
0 引言
电子对抗是使用电磁能等技术手段,控制电磁频谱,削弱或破坏敌方电子信息设备、系统、网络等作战效能发挥,同时保护己方电子信息设备、系统等作战效能正常发挥的作战行动。战场合同作战电子对抗支援行动样式复杂,对其能力进行建模和综合评价是一个难题。目前,合成部队下辖作战支援电子对抗力量,战役战术力量结构与属性也有所调整。因此,对合成部队电子对抗能力进行建模和评估具有较强的现实意义,也是一项比较复杂的系统工程。
目前综合评价方法运用比较广泛的有层次分析、模糊综合评判、数据包络分析、人工神经网络、灰色系统等方法。运用现代综合评价方法对电子对抗装备和行动能力模型进行评估,这方面的研究资料主要有:文献[1]采用层次分析法建立数学模型,对机载电子对抗能力进行了评估和分析;文献[2]建立并规范化电子对抗行动计划的评价指标,将语言评价信息转化为三角模糊数,进而获得计划的综合评价值;文献[3]利用灰色层次分析法,对水声对抗系统进行效能评估;文献[4]围绕雷达、通信、光电等电子装备和系统的工作性能及作战效能,就评估方法、评估准则和评估指标体系三大方面进行了详细介绍。但电子对抗评估领域尚未形成一套公认的理论体系和实施标准。另外,随着电子对抗技术和装备的快速发展,尤其是新体制装备的出现,新战术战法的应用,以及电磁环境复杂程度加剧,电子对抗评估领域面临新的挑战和需求。本文针对新体制下合成部队电子对抗能力建模和评估难度大的问题,重点从行动内容的角度,提出了合成部队电子对抗能力灰色关联评估方法。
1 电子对抗能力评价体系
结合合成部队电子对抗任务,按照电子对抗行动的内容来划分,电子对抗能力评价体系可以分为电子对抗侦察能力、电子干扰能力、电子防御能力[5]3个要素,以及12个三级指标,如图1所示。
2 多层次灰色关联评估方法
灰色系统理论所要考察和研究的是对信息不完备的系统,通过已知信息来研究和预测未知领域,从而达到了解整个系统的目的。1982年,我国著名学者邓聚龙教授首先提出灰色系统理论。他的研究对象是“部分信息已知,部分信息未知”的“贫信息”不确定系统。灰色系统理论主要是利用已知信息来确定系统的未知信息,使系统由“灰色”变为“白色”。该理论最大的特点是对样本量没有严格的要求,与其他统计和评价方法相比,不要求样本服从任何分布。
关联分析是灰色分析、评价和决策的基础。灰色关联分析(grey relational analysis)提供了一种定量分析两个数列集之间相互关联程度的方法。这里采用灰色关联分析评价电子对抗能力的基本思路是:以理想合成部队电子对抗能力各指标值作为参考数列X0的各实体X0k,被评价部队的各指标作为比较数列Xi的各实体Xik,求关联度ri。关联度越大,说明被评价部队指标与理想状态越相似,其电子对抗能力越强;反之,则能力越弱。因此,关联度的大小顺序,就是被评价部队电子对抗能力强弱的次序。
其评价步骤[6-7]如下:
步骤1 确定参考数列
设i为评价单位的序号,i=1,2,…,m;k为评价指标的序号,k=1,2,…n;vik为第i个评价单位的第k个指标的评价值。参考数列应该是一个理想的比较标准,可以以各指标的最佳或最劣值构成参考数列,也可根据评价目的选择其他参照值。这里取每个指标的最佳值的vok参考数列Vo的实际数据,则有:
Vo=(vo1,vo2,…,von)
(1)
式(1)中,vok=Optimum(vik),i=1,2,…,m;k=1,2,…,n。
对一个由m个单位,n个指标的系统,有下列矩阵:
(2)
选取的参考数列为:Vo=(vo1,vo2,…,von)。
步骤2 指标值无量纲化处理
系统各因素物理意义不同,数据量纲也不相同,不便于比较,需要对各指标值进行无量纲化处理。vik为原始指标值,xik无量纲化指标值,处理的目标是为了使各指标数值可横向比较,处理方法如下:
① 初值化
(3)
初值化方法适用于有一定趋势现象的无量纲化,比如呈稳定增长趋势的数列,通过初值化处理,可使增长趋势更加明显。
② 均值化
(4)
一般说来,均值化方法比较适合于没有明显升降趋势现象的数据处理。
③ 区间化
(5)
三种方法不宜混合、重叠作用,在进行系统因素分析时,可根据实际情况选用其中一个。
进行规范化处理后,得:
(6)
步骤3 计算数列之间关联系数
把无量纲化后的数列Xo=(xo1,xo2,…,xon)作为参考数列,Xi=(xi1,xi2,…,xin)(i=1,2,…,m)作为比较数列,分别计算每个比较数列与参考数列对应元素的关联系数:
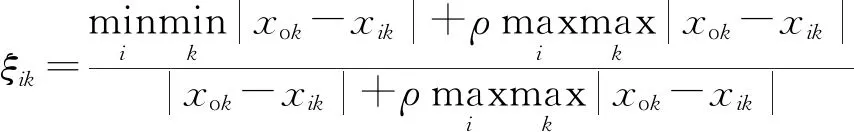
(7)
式(7)中,ρ是分辨系数,ρ∈[0,1],用来削弱Δ(max)过大而使关联系数失真的影响。人为引入这个系数是为了提高关联系数之间的差异显著性。
计算所有关联系数ξik,可得到下列关联系数矩阵:
(8)
步骤4 计算单层关联度
系统各指标的重要性不同,因此单层关联度计算用权重乘关联系数。根据专家调查法、层次分析法法得到某一层的各指标相对于上层目标的权重为:
W=(ω1,ω2,…,ωn)
(9)
R=(ri)1×m=(r1,r2,…,rn)=WET
(10)
步骤5 计算多层最终关联度并排序
计算第k层各指标的关联系数,分别得到它们所属的上一层(即k-1层)各指标的关联度;然后把这一层所得到的关联度作为关联系数,继续计算得到第k-2层各指标的关联度,以此类推,直到求出最高层指标的关联度。
对关联度ri(i=1,2,…,m)大小进行排序,由于采用最优数列作为参考数列,因此关联度的大小顺序即为电子对抗能力优劣次序。
3 实例分析
如图1所述合成部队电子对抗能力指标体系由三层指标组成:第一层目标层,电子对抗能力(B);第二层要素层,包括电子对抗侦察能力(B1)、电子干扰能力(B2)、电子防御能力(B3);第三层指标层,共12个指标。
3.1 确定指标体系各层次权重及综合权重
电子对抗能力各层次指标,依据遂行不同的任务,其权重是不一样的。考虑在一般的合同战斗中,利用专家调查法、层次分析(AHP)赋权[8-9]。层次分析法分值如表1所示。

表1 1~9标度法描述Tab.1 Description of 1~9 sign method
根据表1所述1~9标度法的量化标准,按照各自的重要程度,构造判断矩阵A和Ai(其中i=1,2,3)。
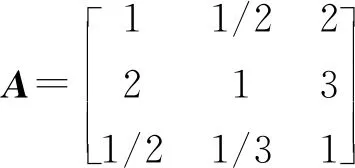
(11)
(12)
(13)
(14)
经过一致性检验,4个判断矩阵CR值分别为0.008、0.02、0.02、0.000 4,均满足CR<0.1,判断矩阵具有一致性,具体层次分析法的过程在这里省略,直接给出结果,各层次单层权重分别为:
合成部队电子对抗能力下一级指标权重:
WB=(0.297 0,0.539 6,0.163 4)
(15)
电子对抗侦察能力下一级指标权重:
WB1=(0.428 7,0.147 2,0.230 3,0.193 7)
(16)
电子干扰能力下一级指标权重:
WB2=(0.428 7,0.147 2,0.230 3,0.193 7)
(17)
电子防御能力下一级指标权重:
WB3=(0.262 7,0.141 3,0.455 0,0.141 1)
(18)
因此,底层指标综合权重如表2、图2所示。从图2中也可以直观地看到,综合权重“电子干扰能力”权重相对较高,“电子防御能力”相对较低;对于合成部队电子对抗行动能力而言,在三级指标中,“通信干扰”所占的权重最大。
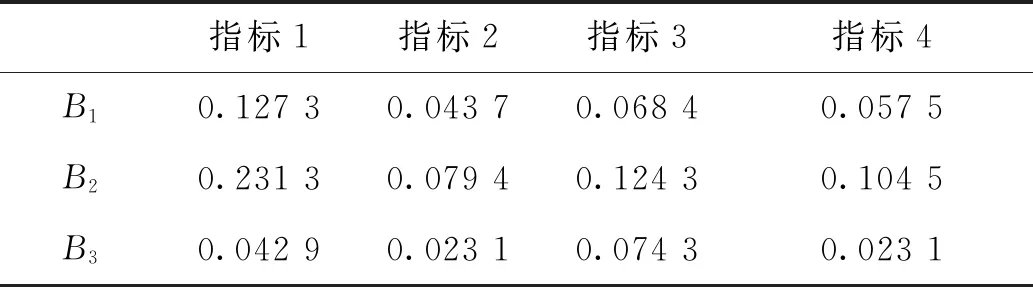
表2 综合权重表Tab.2 Comprehensive weight table
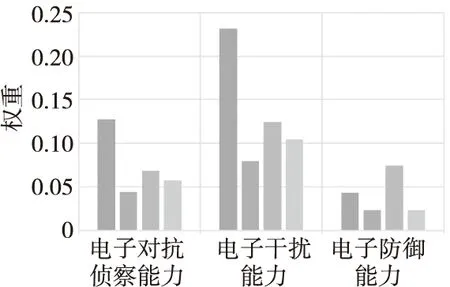
图2 综合权重分布图Fig.2 Comprehensive weight distribution
3.2 确定评价指标的值
电子对抗能力模型的指标类型复杂,量化取值困难。以“通信干扰”性能指标为例,我们可以采集对抗训练或演练中,节点干扰率来表示“通信干扰”性能。节点干扰率是指在一定时间内,敌方战术互联网节点遭我方干扰的程度。节点干扰率越大,干扰效果越好。具体指标为遭干扰节点数量占展开工作节点数量的比率。
设遭干扰的节点数量为Ni,展开工作的节点数量为Nr,则节点干扰率可表示为:
(19)
根据节点干扰率的大小,再进行无量纲化处理。
对于难以定量化处理的指标,例如,“指挥控制”、“机动性能”等,采取结合专项演训数据评估打分的方式得到指标评分,如将指标划分为“优秀”、“良好”、“及格”、“不及格”四级制;[9,10]分为“优秀”,[7,9)分为“良好”,[6,7)分为“及格”,[0,6)分为“不及格”。
其具体评价指标值的过程省略,为便于后期统一衡量,指标值经规范化处理到0~10之间[10-11]。
以4个合成部队的电子对抗能力模拟数据(V1,V2,V3,V4)为例,如表3所示。合成部队V1的特点是通信对抗训练水平高,因此指标B11、B21、B31数值较高;合成部队V2的特点是雷达对抗能力较强,指标B12、B22、B32数值较高;合成部队V3的特点是光电对抗能力较为突出,指标B31、B32、B33数值较高;合成部队V4的特点是各方面比较均衡,没有太突出的指标,也没有短板。参考数列取vok=Optimum(vik),如表3中所示。
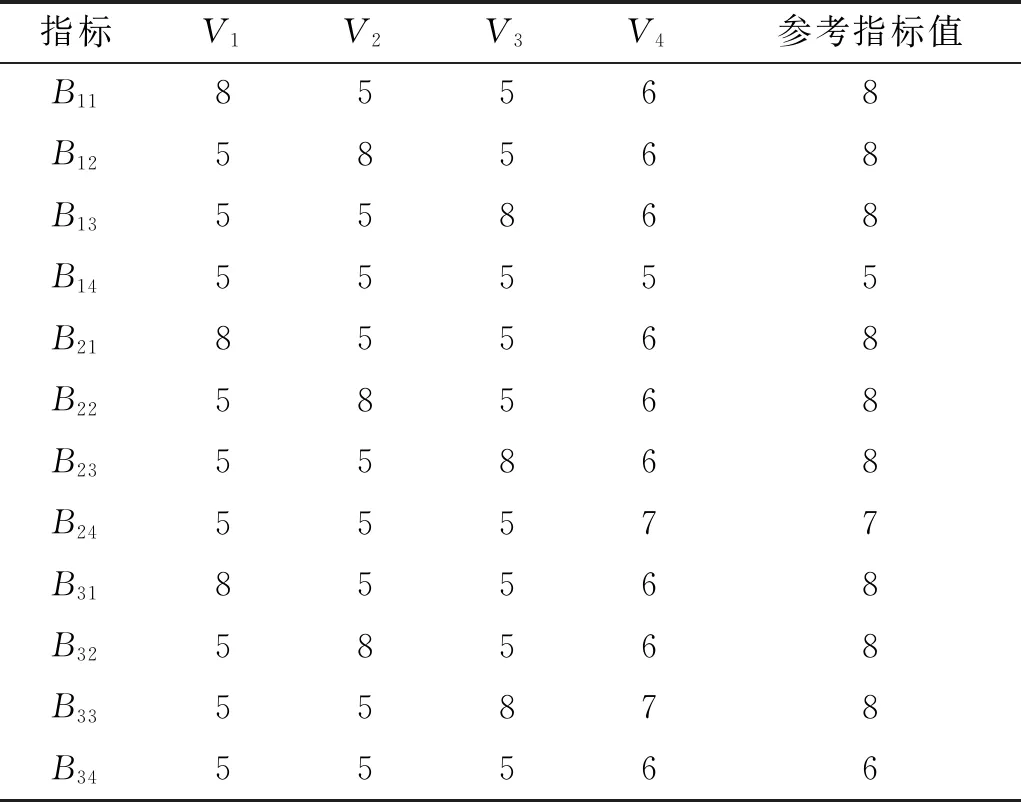
表3 电子对抗能力各指标模拟值与理想值Tab.3 Simulation value and ideal value of each index of electronic countermeasure capability
3.3 计算单层关联度
根据式(8),取分辨系数ρ=0.5,计算得各指标与参考数列的关系系数ξik(i=1,2,…,m;k=1,2,…,n)值列于表4中。
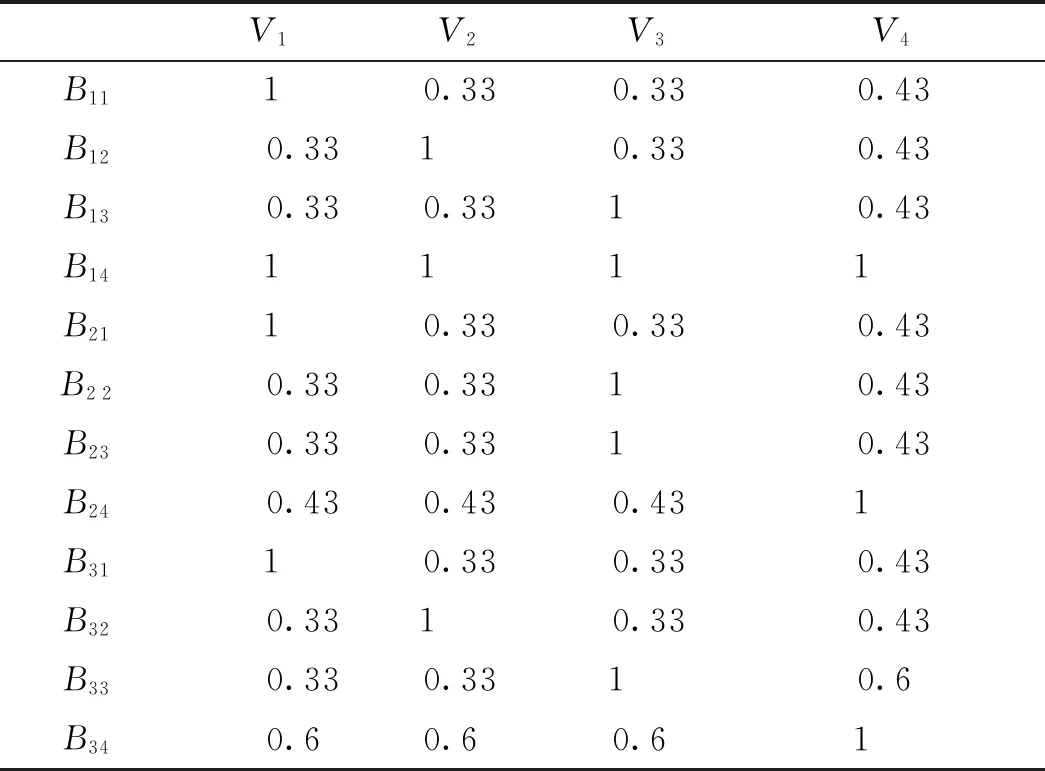
表4 各指标与参考数列关联系数(ξik)表Tab.4 Correlation coefficient of each index and reference series
3.4 多层结构关联度合成
利用公式R=WET可以得到第二层指标的关联度矩阵:
(20)
进一步可求得最高层指标B的关联度,用第一层权重矩阵WB乘以第二层关联度矩阵RBx。
RB=WBRBx=(0.656,0.485,0.566,0.547)
(21)
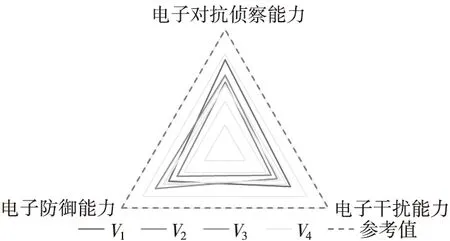
图3 第二层指标关联度雷达图Fig.3 Radar chart of the second level index correlation degree
电子对抗能力排序,总体上四个部队关联度相差不大。按照RB中最终关联度大小,可得到合成部队V1、V2、V3、V4电子对抗能力优劣次序为V1>V3>V4>V2。该结论显示,在该评估体系下,通信对抗水平较高的的合成部队V1,综合评价优于光电对抗能力较为突出的合成部队V3,优于综合指标较均衡的合成旅V4,优于雷达对抗水平较高的合成旅V2。
4 结论
本文提出了合成部队电子对抗能力灰色关联评估方法。首先构建了陆战场电子对抗能力指标体系,而后结合灰色理论与层次分析法(AHP)赋权,对合成部队电子对抗能力进行了综合评价,最后进行了实例分析验证。实例分析证明,该方法能够为合成部队电子对抗能力评估、考核提供理论支撑和依据,下一步还将进一步进行数据实践。与过去的模型和方法相比操作简单、适用性强、结论科学,便于对多个单位电子对抗能力进行分析比较评判。对合成部队电子对抗能力建设发展、科学化考核评估具有重要的理论意义和实际价值。针对具体行动完善电子对抗能力指标体系与改进综合评价方法。
