基于粒子群遗传算法的三轴磁通门误差校正
2021-07-20吕俊伟陶荣华
迟 铖,王 丹,吕俊伟,陶荣华
(1.海军潜艇学院遥感所,山东 青岛 266001;2.山东华宇工学院,山东 德州 253000)
0 引言
磁通门磁力仪作为一种磁场三分量测量仪器,具有灵敏度高、体积小、价格相对较低的优点,在地磁导航、铁磁性目标探测[1-3]等领域得到了广泛的应用。然而在磁通门磁力仪实际的制造过程中,受加工技术工艺的限制,磁通门磁力仪的三个测量轴存在三轴非正交、灵敏度不一致、零点偏置等误差,使得磁场的测量值与实际值之间存在着较大的误差,严重影响磁通门磁力仪的测量精度,因此磁通门磁力仪在使用前首先需要对其进行误差校正。
目前国内外的学者在磁通门磁力仪的误差校正方面开展了大量的研究,常见的方法主要分为矢量校正和标量校正两大类。矢量校正[4-5]需要利用高精度的三轴无磁转台提供磁通门磁力仪实时的姿态,该方法实现过程较为复杂,因此仅适用实验室条件下对磁通门磁力仪进行校正;标量校正[6-11]通过将磁通门磁力仪放置于匀强磁场中,通过测量不同姿态下的数据后进行拟合得到校正参数,该方法不需要高精度的辅助测量仪器,且操作简单,因此是目前较为常用的校正方法。文献[8]提出了一种利用简化模型对误差进行校正的方法,但是该方法的校正精度不高;文献[9]通过对校正参数进行两次非线性转换,然后利用线性最小二乘法实现对校正参数的估计,但是该方法的转换过程复杂;文献[10]提出了一种基于蚁群算法的三轴非正交误差校正方法,但未考虑三轴灵敏度不一致和零点漂移等误差;文献[11]提出了一种利用遗传算法来求解校正参数的误差校正方法,但是该方法受初始参数的影响较大。本文针对目前磁通门磁力仪误差校正方法中存在的校正精度不高和受初始参数影响较大的问题,提出了基于粒子群遗传算法的三轴磁通门误差校正方法。
1 磁通门磁力仪的误差模型
磁通门磁力仪的误差主要包括三轴非正交误差、灵敏度误差和偏置误差。三轴非正交误差指的是实际磁通门磁力仪的各个测量轴之间不是完全正交的,建立如图1所示的坐标系。
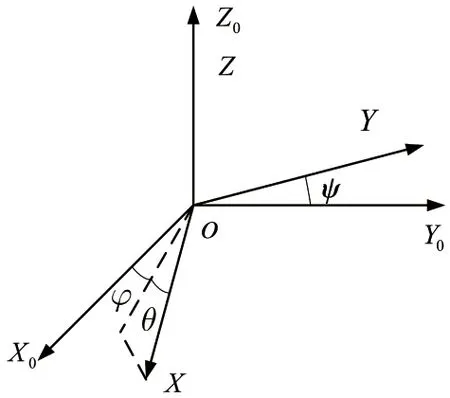
图1 三轴非正交误差示意图Fig.1 Schematic diagram of the model of three axial non-orthogonal error
O-X0Y0Z0为理想的三轴正交坐标系,O-XYZ为磁通门磁力仪实际的测量坐标系。假设测量轴OZ与坐标轴OZ0重合,且指向一致,将坐标系O-XYZ沿着OZ轴旋转,使得测量轴OY与Y0OZ0在同一个平面上,测量轴OY与坐标轴OY0之间的夹角为ψ,测量轴OX与X0OY0平面之间的夹角为θ,测量轴OX在X0OY0平面的投影与坐标轴OX0之间的夹角为φ。灵敏度误差指的是磁通门磁力仪的三个测量轴的灵敏度不一致导致的误差,假设三个测量轴OX、OY、OZ的灵敏度分别为kx、ky、kz。偏置误差指的是当磁通门磁力仪放置于磁场强度为0 nT的环境中时,三个测量轴仍会输出小的偏移量,假设三个测量轴的偏置为b=[bx,by,bz]T。
综合考虑磁通门磁力仪的三轴非正交误差、灵敏度误差和偏置误差,得到磁力仪的测量值与实际值之间满足的关系如下:
Bm=SCNOB+b+ε
(1)
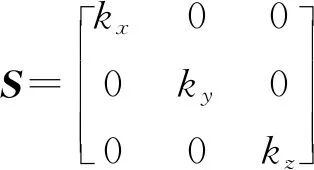
2 基于粒子群遗传算法的磁通门误差校正
2.1 磁通门磁力仪误差校正模型
根据式(1),磁通门磁力仪的误差模型可以简化为如下形式:
Bm=CB+b+ε
(2)
式(2)中,C=SCNO为综合误差矩阵,相对于磁力仪的误差而言,磁力仪的测量噪声可近似忽略不计,因此误差模型可以简化成如下形式:
B=C-1(Bm-b)
(3)
式(3)即为磁通门磁力仪的误差校正模型,由式(3)可得,只要求得C-1与b便可以实现将磁通门磁力仪的测量值转换成磁场的实际值,实现对磁通门磁力仪的误差校正。
目前的标量校正指的是,将磁通门磁力仪放置于一个均匀的磁场中,则磁场总场为一个定值,根据误差校正模型式(3)可得:
BTB=(Bm-b)T(C-1)TC-1(Bm-b)=const
(4)
通过改变磁通门磁力仪的不同姿态,则可以获得多组测量值,通过标量磁力仪可以监测背景磁场的总场值,则根据式(4)可以拟合求出需要校正的各个参数。
2.2 基于粒子群遗传算法的校正参数求解
1995年,Kermey和Ebethart博士根据鸟群寻找食物的行为,提出了粒子群算法[12-13],粒子群算法的核心体现在单个追踪粒子通过自身的先前经验和共享集体最优信息来实现向最优空间搜索。传统的粒子群优化算法具有搜索速度快的优点,但是容易陷入局部最优,因此本文将粒子群遗传算法应用到磁通门磁力仪的误差校正中,从而实现全局最优解的搜索。
首先进行粒子位置和速度的初始化参数设置,磁通门磁力仪的误差校正问题相当于9个校正参数的求解问题,因此位置和速度都是9维空间。假设粒子群中共有m个粒子,xi=(xi1,xi2,…,xi9)为第i个粒子当前的位置矢量,位置矢量中每列代表的参数分别为kx、ky、kz、bx、by、bz、ψ、φ、θ,vi=(vi1,vi2,…,vi9)为第i个粒子当前的速度矢量。粒子的位置矢量即为优化问题的潜在解,通过适应度函数f(x)来描述粒子的位置的好坏。磁通门磁力仪误差校正的适应度函数为:
(5)
式(5)中,Be指的是地磁场的模,可通过标量磁力仪测量得到;N为磁通门磁力仪的测量姿态数。通过式(5)可得,当校正后的磁场值与地磁场的模之间的差值越小,表示校正后的值与地磁场越接近,因此校正效果越好。
pi=(pi1,pi2,…,pi9)为第i个粒子的历史最优位置,个体最优位置由下式进行更新计算:
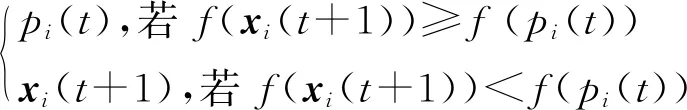
(6)
式(6)中,t代表迭代的次数。全局最优位置p(t)定义为群体中所有粒子目前所经历过的所有状态中的最优位置,则:
g(t)=min{f(p1(t),f(p2(t),…,f(pm(t)}
(7)
粒子通过自己的个体最佳位置和种群的全局最佳位置决定下一步的飞行方向和距离。粒子的位置和速度根据以下的公式进行更新:
vi(t+1)=ωvi(t)+c1r1(pi(t)-xi(t))+
c2r3(gi(t)-xi(t))
(8)
xi(t+1)=xi(t)+vi(t+1)
(9)
式(8)、式(9)中,ω为惯性因子,c1和c2为加速因子,r1和r2是[0,1]之间的随机数。
上述为传统的粒子群算法,该算法可以快速收敛得到误差校正参数,但是容易陷入局部最优解,因此本文采用粒子群遗传算法对校正参数进行求解,具体做法如下:每次迭代后将粒子按照适应度值由小到大进行排序,为保证适应度较优的粒子个体能存活下来,将适应度较优的前一半粒子直接进入下一次迭代,将适应度较差的后一半粒子进行交叉和变异操作,来防止进入局部最优,提高算法的全局搜索能力。
3 仿真分析
为了验证本文所提方法的有效性,设计仿真实验进行验证,仿真实验条件设定为假设将磁通门磁力仪放置于均匀的地磁场中,地磁场的总场大小为51 800 nT,三轴磁通门磁力仪的各个误差参数如表1所示。

表1 误差参数表Tab.1 Error parameters
磁通门磁力仪的精度为0.1 nT,仿真时在磁通门磁力仪的三个测量轴上分别加入方差为0.1 nT的高斯白噪声,选取200个姿态下的磁力仪测量数据,磁通门的原始测量数据如图2所示。由图2可得,未校正前磁通门磁力仪的测量值误差较大,在均值为51 800 nT的地磁场中,测量的磁场总场最大偏差值可达到1 862.8 nT,不同状态下磁场总场的波动峰峰值为3 511 nT,因此需要对原始测量数据进行校正后才能使用。
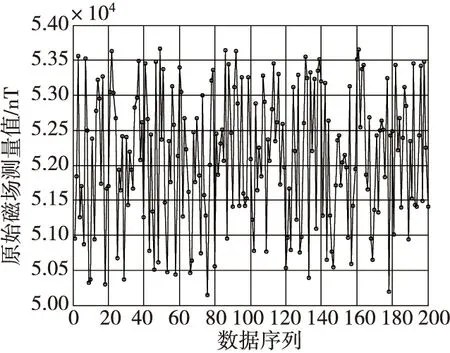
图2 磁通门磁力仪的原始测量值Fig.2 Raw data measured by fluxgate magnetometer
本文利用粒子群遗传算法(PSO-GA)和传统粒子群算法(PSO)分别进行校正参数的求解。同时为了将本文方法与现有校正方法进行对比,增加了文献[8]提出的线性化校正方法的校正效果作为对比。
粒子群遗传算法(PSO-GA)的参数设定为,粒子群的数目为1 000,迭代次数为100,加速因子c1取1.5,加速因子c2取1.8,惯性因子ω取0.8。仿真结果如表2所示。表2为利用粒子群遗传算法和传统粒子群算法得到的误差校正参数。
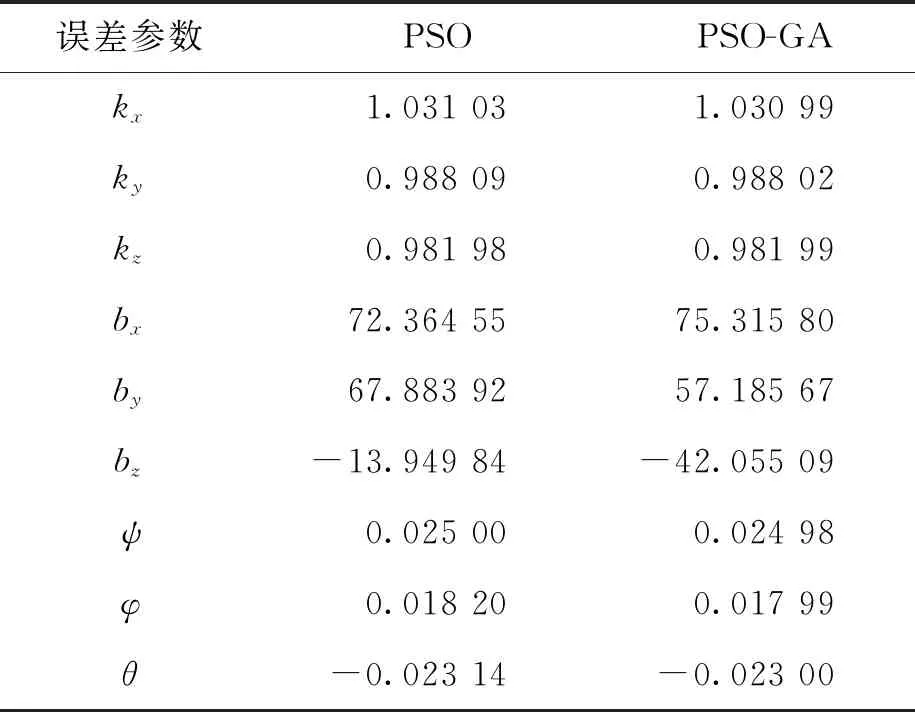
表2 误差参数估计值表Tab.2 Estimate value of error parameters
由表2可得,PSO-GA算法计算得到的参数估计误差较小,对bx的相对估计误差最大,为0.42%;PSO算法计算得到的偏置误差参数值误差较大,对bz的相对估计误差最大,为66.8%。图3给出了PSO和PSO-GA两种算法在历次迭代中适应度值的变化,可用于对比两种算法的收敛性能。
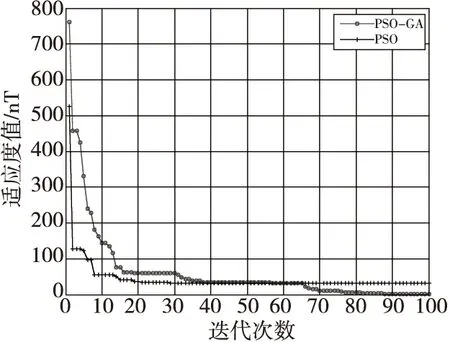
图3 PSO和PSO-GA两种算法在历次迭代中适应度值变化Fig.3 The fitness value variation of PSO and PSO-GA algorithm
由图3可知,总共迭代次数为100次,传统的粒子群算法在初期收敛较快,但是未收敛到最小值,且在算法计算的后期便不再进行优化;而粒子群遗传算法从迭代的初期就迅速收敛,并且在算法后期也继续收敛,直到达到较小的适应度值,因此可以看出PSO-GA可以增加算法的全局最优搜索能力。
图4为不同校正方法对磁场总场校正前后的对比图。由图4可得,三种方法均能实现对磁通门磁力仪的误差校正,但是文献[8]的线性化校正方法由于忽略了二阶小量,因此校正的误差较大,校正后的磁场总场最大偏差为1 019.6 nT,磁场总场的波动峰峰值为1 335 nT;而PSO-GA算法与PSO算法的校正效果较好,PSO算法对磁场测量值进行校正后的磁场总场最大偏差可达30.5 nT,磁场总场的波动峰峰值为60.4 nT;PSO-GA算法的计算效果更好,校正后的磁场总场最大偏差为1.2 nT,磁场总场的波动峰峰值为2.1 nT,因此基于PSO-GA算法可以提高磁通门磁力仪误差校正的精度。

图4 磁场总场校正前后对比图Fig.4 Comparison of total magnetic intensity before and after calibration
为了更直观地显示三种校正方法的校正效果,我们将磁场三分量的校正值与实际值之差进行比较,结果如图5—图7所示。
由图5—图7可得,PSO-GA算法与PSO算法的校正结果均优于文献[8]校正方法的校正结果,且文献[8]中对于Z分量的校正效果较差,校正值与实际值最大的偏差可达-1 019 nT。而PSO-GA算法的各分量校正值与实际值最大的偏差为-1.4 nT。

图5 X分量校正值与实际值之差对比图Fig.5 Comparison of difference between calibrated X outputs and actual outputs
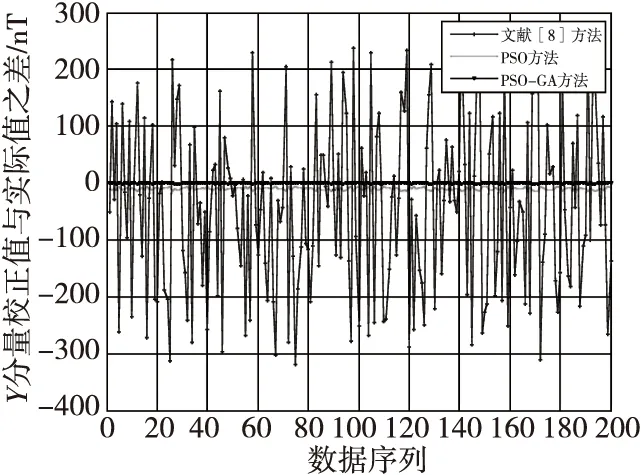
图6 Y分量校正值与实际值之差对比图Fig.6 Comparison of difference between calibrated Y outputs and actual outputs

图7 Z分量校正值与实际值之差对比图Fig.7 Comparison of difference between calibrated Z outputs and actual outputs
定义均方根误差的计算公式:
(10)
式(10)中,Bi为磁场的实际值,Bci为磁场的校正值。则根据式(10)得到不同校正方法的均方根误差如表3所示。
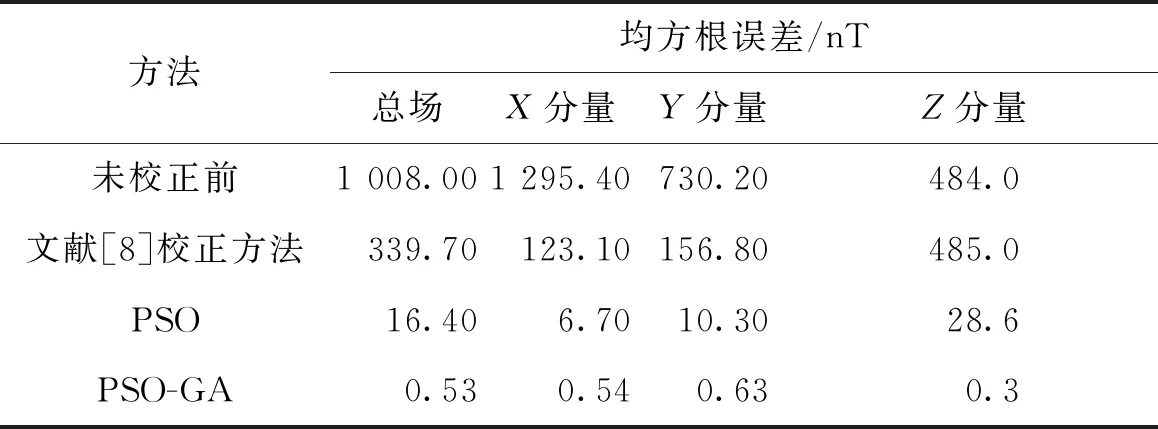
表3 校正前后的均方根误差对比表Tab.3 Comparison of root-mean-square errors before and after calibration
由表3可得,由于文献[8]中对误差模型线性化时假设Z轴的灵敏度为1,因此通过校正结果来看,Z轴的校正误差较大。而本文提出的PSO-GA校正方法,校正后的均方根误差与仿真实验时加入的高斯白噪声在同一量级,因此得出PSO-GA校正方法可以实现对磁通门磁力仪的精确校正。
4 结论
本文提出了基于粒子群遗传算法的磁通门误差校正方法。该方法首先在分析误差产生机理的基础上建立了误差校正模型,随后利用粒子群遗传算法来求解校正参数,该算法通过对粒子群中的适应度较差的粒子进行交叉、变异操作来增加算法的全局最优搜索能力。分别利用传统粒子群算法和粒子群遗传算法对磁通门磁力仪的误差进行了校正仿真实验。仿真实验结果表明,与传统的粒子群优化算法相比,基于粒子群遗传算法的误差校正能快速地收敛,且具有较强的全局最优搜索能力,可以实现对磁通门磁力仪的高精度校正。
