基于MHMM的导引头伺服机构机械故障智能诊断

罗进海, 张 乐, 马辉辉, 朱 骏, 蒋会明

(1.上海理工大学,上海200093;2.上海无线电设备研究所,上海201109)

0 引言

随着现代科技的迅速发展,机械设备逐渐朝着复杂化、精密化和高度自动化方向发展,其运行可靠性与安全性问题得到了研究学者越来越多的关注。导引头伺服机构是导弹实现目标跟踪和视线轴稳定功能的重要执行机构,对于实现和保障导弹既定性能起重要作用[1]。导引头伺服机构结构精细、复杂、易损,服役环境恶劣,机械结构的任何微小故障都有可能降低导弹性能,引发难以估计的后果。因此,导引头伺服机构机械故障诊断具有迫切的工程需求与重要的实际意义。

导引头伺服机构运行工况复杂,伺服机构的监测信号具有强非线性、非平稳与强噪声干扰的特点。基于传统的时频域分析的故障诊断方法遭遇重重阻碍,基于机器学习的方法成为解决该问题的主要途径。隐马尔可夫模型(hidden Markov model,HMM)作为一种时序统计概率模型,具有隐状态链与观测序列链双重随机属性,在设备状态监测和早期微弱故障诊断领域应用广泛。“机械故障发于内,而形于外”,机械设备的微小故障状态虽然难以直接从其外在表现,如振动、声音和温度等变化来判断,但却是其外在表现发生微不可见的变化的根本原因。这与隐马尔可夫模型具有的观测序列链与隐状态链的双链属性在本质上是相通的。因此,HMM非常适合用于导引头伺服机构机械故障的智能诊断。

OCAK等[2]提取轴承运行状态振动信号特征值矩阵,构建 HMM 实现故障诊断。PURUSHOTHAM等[3]将离散小波变换和HMM相结合,成功实现轴承的多故障分类。DONG等[4]将隐半马尔可夫模型用于泵的故障诊断和寿命预测研究。刘韬等[5]提出基于核主成分分析和耦合隐马尔可夫模型的轴承多通道融合故障诊断方法。袁洪芳等[6]则将HMM与改进距离测度法相结合,有效识别齿轮箱轴不对中、断齿、磨损等多种故障模式。

本文针对导引头伺服机构多通道监测数据特点,引入多链隐马尔可夫模型(multi-chain hidden Markov model,MHMM)。基于 MHMM 的多观测序列链、单隐状态链的动态网络结构,同步智能提取多通道数据所蕴含的多维统计特征规律,实现对机械设备故障状态的精确表征,并基于伺服机构机械故障试验数据验证所提方法的有效性。

1 基本原理

特征提取方法和机器学习方法涉及机械故障智能诊断的关键步骤与核心理论。针对导引头伺服机构监测信号的特点,结合多测点多通道采样的工程实际,引入基于时域统计特征的特征提取方法和多链隐马尔可夫模型这一统计概率模型。

1.1 时域统计特征提取

时频域信号处理与特征提取技术的发展为监测信号特征提取提供了丰富的途径。然而,导引头伺服机构监测信号强非线性、非平稳和强噪声干扰的特点,导致时频域特征的提取受到噪声、工况等非线性因素与多参数优化方法的制约。因此,计算简单的时域统计特征提取方法在工程实际中常被作为表征设备运行状态的监测指标。

工程中常用的时域统计特征分为两类:有量纲参数指标和无量纲参数指标。其中,典型的有量纲参数指标(如均值、标准差、方根幅值、均方根值、峰值)对数据变化极其敏感,但会受到设备运行工况的干扰;而无量纲参数指标(如峭度指标、波形指标、峰值指标、脉冲指标、裕度指标)具有对信号幅值及频率变化不敏感的特点[7]。在10个常用的时域统计特征中,峰值、峭度指标、波形指标、峰值指标、脉冲指标等对机械设备的早期冲击故障比较敏感,而均方根值和波形指标等则可以实现对机械设备退化过程的稳定表征。本文在导引头伺服机构机械故障智能诊断中,将有量纲及无量纲参数指标共同作为故障特征进行提取,各特征参数计算公式如表1所示。

表1 时域统计特征计算公式

1.2 MHMM基本原理

导引头伺服机构运行工况复杂,测试干扰因素众多,即使是同一种故障状态也常常表现出不同的外在征兆。因此,仅依靠单一通道监测数据难以得到准确的诊断结果。为此,本文基于多链马尔可夫模型来智能融合多通道数据,获得监测数据所表征的底层特征规律,为导引头伺服机构机械故障诊断提供可靠依据。

HMM是一个典型的统计概率模型,具有符合Markov性质的隐状态链和随机分布的观测值序列链的双随机链结构。通常,典型的HMM可以表示为

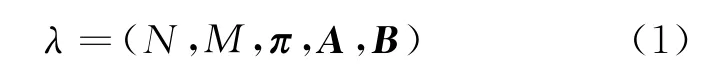
式中:N为模型的隐状态数目,记模型的N个隐状态为S1,S2,…,S N,q t∈{S1,S2,…,S N}为t时刻模型所处的状态;M为每个隐状态可能的观测值数目,记M个观测值为v1,v2,…,v M,t时刻的观测值为o t,则有o t∈{v1,v2,…,v M};π={πi,1≤i≤N}为初始状态概率向量,其中πi=P(q t=S i),P(·)表示概率分布函数;A=[a i,j]为状态转移概率矩阵,其中a i,j=P(q t+1=S j|q t=S i),1≤i,j≤N;B=[b j,k(o t)]为观测值概率矩阵,其中b j,k(o t)=P(o t=v k|q t=S i),1≤j≤N,1≤k≤M。

由于工程中实际采集到的多为连续信号的离散值,因此常采用混合高斯分布(Gaussian mixed model,GMM)来拟合不同状态下的观测值概率。另外,导引头伺服机构采样数据涉及多通道采样,需采用多观测值序列的MHMM来拟合观测数据的分布规律。MHMM的贝叶斯网络结构如图1所示,其中,C为观测序列的链条数,T为最大时刻。

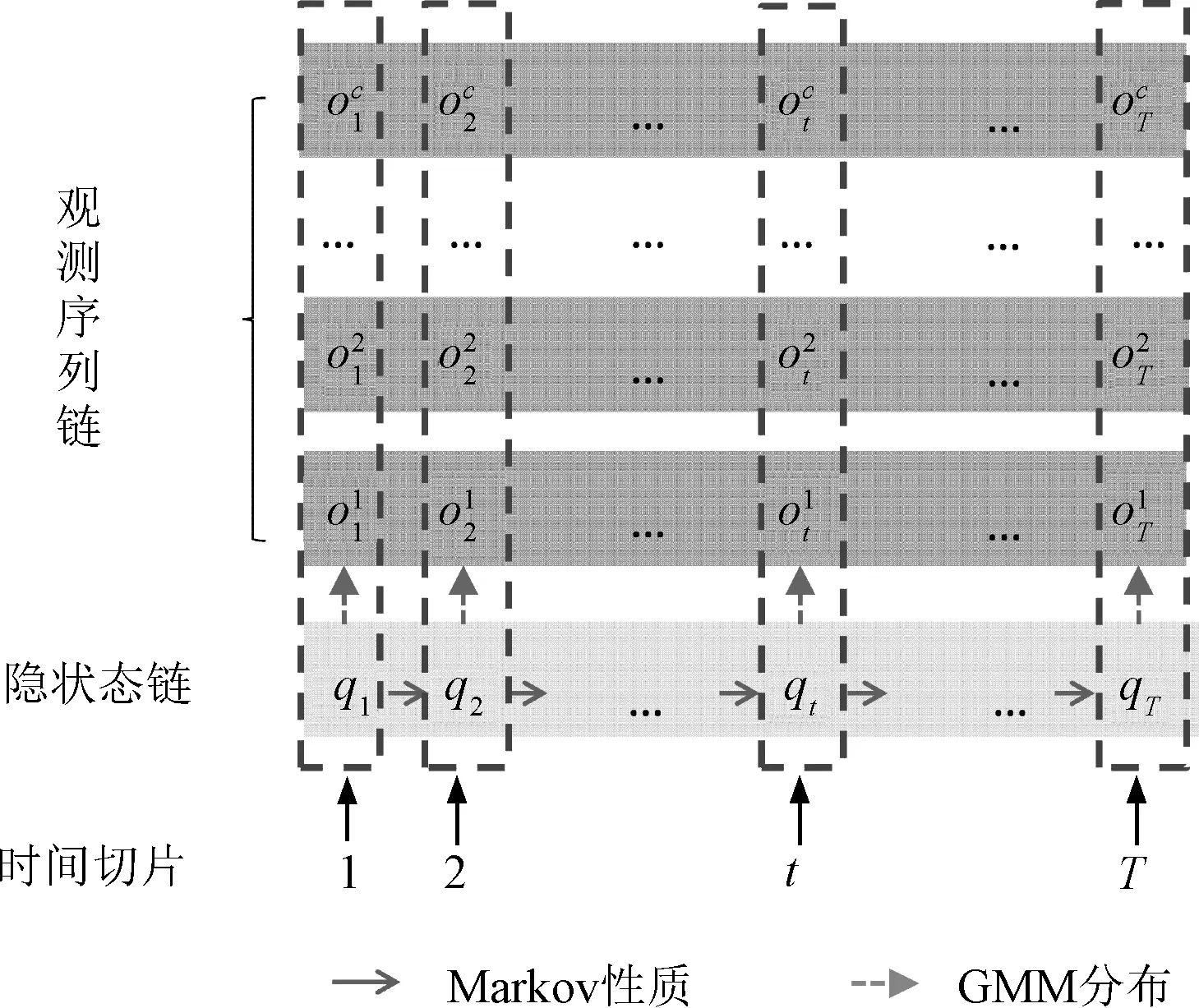
图1 MHMM的贝叶斯网络结构图

图1中,MHMM包含观测序列链与隐状态链两部分,其中观测序列链由多条组成。每个隐状态下的多元观测序列服从GMM分布,隐状态链具有Markov性质,每一个时间切片内的多通道数据依赖于同一个隐状态参数。这与设备的故障机理是相通的,虽然不同通道对设备状态的表征不同,但是他们都是设备同一个故障状态的表征。因此,MHMM具有多通道信息融合的能力,非常适合用于导引头伺服机构机械故障的多通道融合诊断。另外,MHMM应用中所涉及的3种经典算法在文献[8]中已有详细说明,此处不再赘述。

2 基于MHMM的多通道融合智能故障诊断

故障诊断是一个模式识别的过程,它将采集的数据或提取的特征映射为设备的故障类型。基于MHMM的多通道融合故障诊断分为离线训练和在线测试两大部分,具体包含数据采集、特征提取、MHMM训练以及故障诊断等4个基本步骤,对应故障诊断流程如图2所示。其中,λi(i=1,2,…,I)为训练得到的 MHMM,I为模型数量;为待测设备在模型λi中的输出似然概率。

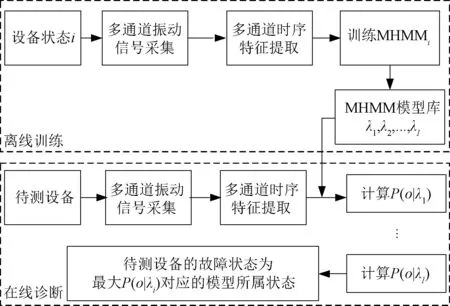
图2 基于MHMM的多通道融合智能故障诊断流程

在离线训练时,针对每一种设备状态(正常与各种故障状态)分别训练一个MHMM模型,具体步骤为:

a)数据采集,分别通过多个传感器采集每种故障状态下的多通道振动信号;

b)特征提取,将信号划分为多个时窗信号,针对每个时窗信号分别提取时域统计特征向量,构建多通道振动信号特征向量序列,得到MHMM训练所需的多通道观测序列集;

c)HMM训练,基于Baum-Welch算法将提取的多通道特征向量序列输入到MHMM中进行参数估计,将得到的每种故障状态的MHMM参数存入模型库中。

在在线故障诊断环节,首先对待测设备进行数据采集和特征提取,得到多通道时序特征向量序列,将其输入到模型库中的各个MHMM中,计算各模型的输出似然概率,其中输出最大似然概率的模型对应的故障状态即为待测设备故障状态。

3 工程案例分析

由于导引头伺服机构的精密紧凑性,包含多级齿轮传动的内置平台相对齿弧回转的俯仰通道易形成损伤。基于正常机构(指结构完好的机构)和局部损伤机构的采样数据,验证基于隐马尔可夫模型的导引头伺服机构机械故障智能诊断方法的有效性。

3.1 试验介绍

分别对两套相同型号的导引头伺服机构进行随机振动试验,其中一套为正常机构,一套为局部损伤机构。导引头伺服机构简化模型如图3(a)所示。试验时,方位通道锁死,在预定回路状态下对伺服控制系统输入三角波信号,分别驱动伺服机构内置俯仰框和齿弧,使俯仰通道以绕水平面±40°的三角波形式运动。试验中的三角波信号主频率分别设为0.2,0.3,0.4,0.5,0.6,1.0 Hz,6种伺服控制信号频率对应6种工况,采样频率设为1 024 Hz。在俯仰框传动链末级,采用Co-Co-80振动数据采集器采集振动信号,测点位置如图3(b)所示。共布置6个测点同步采样,其中测点1、4和5向下,测点2和3向左,测点6位于轴向。正常机构俯仰通道转至下极限位置时有异响,可能在末级扇齿处有焊线时掉落的焊锡,方位通道齿弧处发现焊锡。

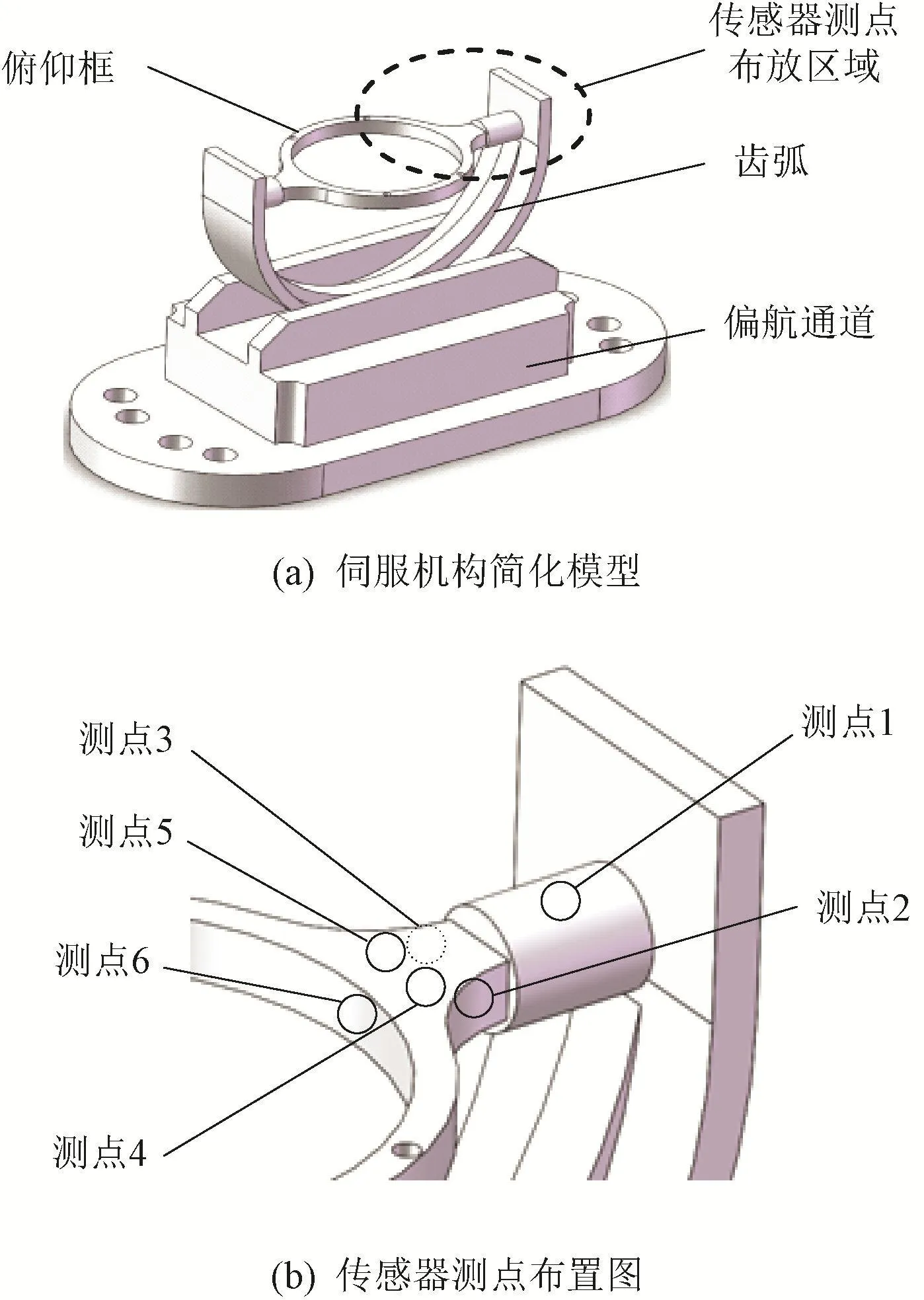
图3 伺服机构简化模型及传感器测点布放区域

3.2 数据分析

图4为正常机构0.2 Hz工况下测点1振动数据的时频域图。正常机构的主特征频率是转频及其二倍频,其中二倍频处的较大振幅对应正常机构俯仰通道转至下极限位置处的异响情况。

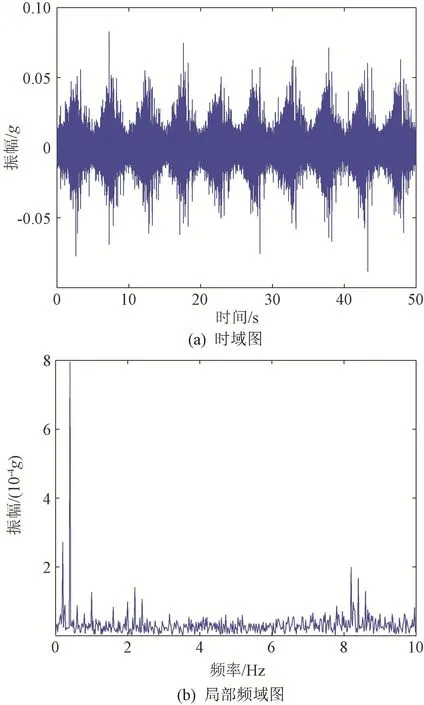
图4 正常机构0.2 Hz工况测点1振动时频域图

图5为局部损伤机构0.2 Hz工况下测点1振动数据的时频域图。局部损伤机构的振动频谱呈现为转频及其多阶倍频,难以从频谱图中找到对应的故障频率成分。经典的时频分析方法,如经验模态分解[9]或变分模态分解[10]等,亦难以有效地提取出所需固有模态。因此,直接基于信号分析的故障诊断方法难以实现对导引头伺服机构故障的有效诊断。

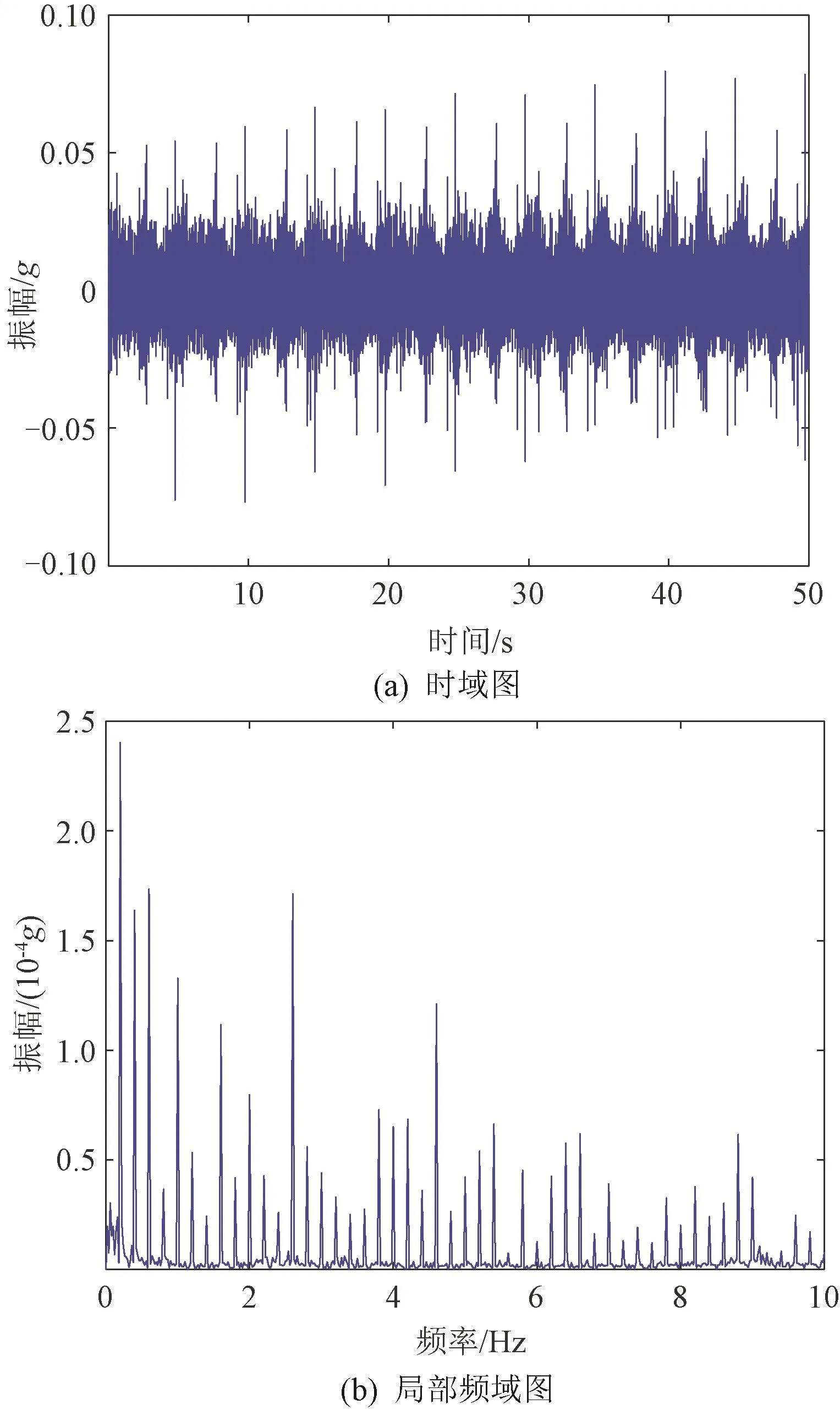
图5 局部损伤机构0.2 Hz工况下测点1振动时频域图

3.3 智能诊断结果分析

在多通道信号特征提取环节,首先,将正常机构和局部损伤机构的多通道振动信号分别进行分段处理,每个采样通道的每次采样分为10个时窗;然后,针对每个时窗分别提取10个常见时域统计特征;最终形成6个通道10个连续时窗的10维时域统计特征向量库。试验中针对正常机构和局部损伤机构分别提取了100个样本,各随机选取50个样本作为训练数据集,剩余50个作为测试数据集。基于离线训练流程,采用训练数据集为每种工况下的正常状态和局部损伤状态分别构建模型,建立导弹伺服机构故障状态模型库。

将6种工况下的测试数据集分别输入故障状态模型库,将其中输出似然概率最大的模型所对应的故障状态作为被测机构所处的故障状态。6种工况下局部损伤机构采样数据在故障状态模型库中的测试结果如图6所示。在所有工况下,测试数据在两种不同故障状态模型下的输出似然概率差异十分明显,诊断结果与真实情况相符。将正常机构测试数据输入到模型库中进行测试,同样得到正确分类。结果表明,在不同工况下,正常机构数据及局部损伤机构数据的诊断准确率都可以达到100%,本文所提方法可以有效实现不同工况下正常机构与局部损伤机构的智能诊断。

为进一步验证基于MHMM的多通道融合故障诊断方法的有效性,基于6个测试通道数据分别做故障诊断。同样50%数据用于模型训练,50%数据用于模型测试。不同工况下基于单通道采样数据的平均诊断准确率如表2所示。

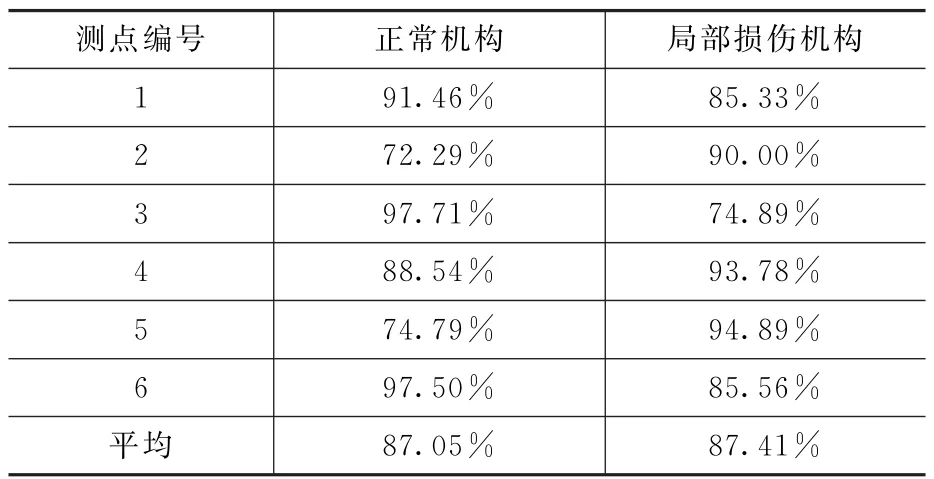
表2 单通道采样数据平均诊断准确率

由表2可知,利用不同测点的传感器数据单独进行测试时,故障诊断的准确率波动较大。且由于正常机构俯仰框转至下极限位置会有异响,在使用单传感器测试时结果易受到干扰,导致诊断准确率偏低。而MHMM的多链动态网络结构使其可以同步智能提取多通道观测数据链背后所隐藏的统计规律,实现多通道信号的智能融合,有效降低单个通道中的干扰因素,提高智能诊断的正确率。

4 结论

针对导引头伺服机构结构局部损伤难以基于传统时频域信号分析方法进行有效诊断的问题,提出一种基于多链隐马尔可夫模型的多通道特征融合机械故障智能诊断方法。MHMM具有多观测序列链、单隐状态链的动态网络结构,能够同步智能提取多通道数据所蕴含的多维统计特征规律,实现对机械设备故障状态的精确表征。基于MHMM的伺服机构机械故障智能诊断方法实现了对导引头伺服机构正常与局部损伤状态的有效诊断。同时,通过多通道信号融合前后对比试验,验证了所提方法的优越性,为导引头伺服机构健康状态监测与智能诊断应用提供了有效途径。