开关磁阻电机自抗扰调速优化控制研究

王琴剑，戴跃洪

（1.电子科技大学航空航天学院，四川成都，611731；2.电子科技大学航空航天学院，四川成都，611731）

0 引言

开关磁阻电机（switched reluctance motor,SRM）是一种最具潜力、高效节能的机电一体化产品，其结构简单、运行可靠及效率高的特点使此类电机在工农业生产等各领域迅速得到了广泛的应用。由于SRM转子的双凸极结构并且其步进电磁场长期运行在饱和与非线性状态，很难得到简单、统一的数学模型和解析式。因此SRM调速系统是一个便参数、非线性、强耦合的时变复杂系统[1]。适用于线性系统的经典PID（比例-积分-微分）控制不能很好的应用在开关磁阻电机的调速系统。文献[2]介绍了一种模糊PID的控制策略，但其控制效果依赖模糊规则的建立，建立模糊规则需要作者有丰富的调试经验。文献[3]介绍了一种基于在线柔性神经网络的控制方法，虽然能够达到足够的动态和静态稳定性，但实际的驱动控制器可能并不具备足够的算力，这种方法只能停留在实验室阶段。

自抗扰控制（active disturbance rejection control,ADRC）技术是有中科院韩京清研究院在经典PID控制的基础上改进后形成的一种新型控制方法[4]。相较于传统的PID控制，ADRC引入了跟踪微分环节来对系统进行滤波和跟踪，引入了现代控制论中的状态观测器来对系统中的状态进行在线调整，使得系统具有更低的超调，更快的响应速度，以及更强的适应性和抗干扰能力。目前已经广泛的应用于机床、电力系统、电动汽车等领域。但ADRC控制参数较多，参数整定麻烦，于是涌现除了很多针对ADRC的优化算法。文献[5]通过系统辨识技术得到SRD大致的传递函数，然后使用文献[6]所提供的方法对参数进行取值并进行调试，这种方法的优点是简单高效，缺点也很明显，精度太低，无法得到最优的参数。文献[7]提出了基于强化学习的自抗扰控制参数在线整定，这种方法可以得到最优的参数，但由于在线学习在控制环需要时间成本，加上一般的电机驱动器算力不够，系统的快速性可能会比较差。

本文采用非线性ADRC设计SRM速度环控制器，利用混沌粒子群算法来对自抗扰控制器进行在线调优，并通过仿真对控制效果进行验证。

1 开关磁阻电机调速系统

■1.1 开关磁阻电机调速系统

本文所采用的开关磁阻电机调速系统的结构如图1所示。

图1 开关磁阻电机调速系统

该系统主要包括速度环控制器、直接转矩控制器、功率变换器、开关磁阻电机、转矩检测、角度检测、速度计算这6个部分组成。参考速度信号输入后，和速度传感器检测得到的速度信号做差，得到速度环控制器的输入，速度控制器输出参考转矩，参考转矩与转矩检测器测得的实际转矩进行做差，将差和角度传感器得到的当前角度信号作直接转矩控制器的为输入，得到多路脉冲调制(pulse width modulation,PWM)信号，功率变换器依照PWM信号输出电压，驱动电机。

■1.2 开关磁阻电机数学模型

开关磁阻电机是一种双凸极电机，它的定子和转子都是由硅钢片叠压而成，其运行原理遵循“磁阻最小原理”—磁通总要沿着磁阻最小的路径闭合。其第k相的电压方程如式（1）所示：

其中磁链 为电流ki和转子位置角θ的函数，

将（2）带入（1）可得：

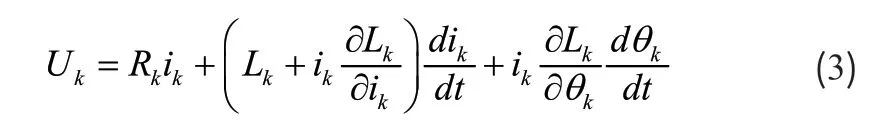
转子的机械方程为：

转子机械方程和电压电流方程是由磁储能Wf和磁共能Wfc联系起来，在任意一点的瞬时合成转矩为：

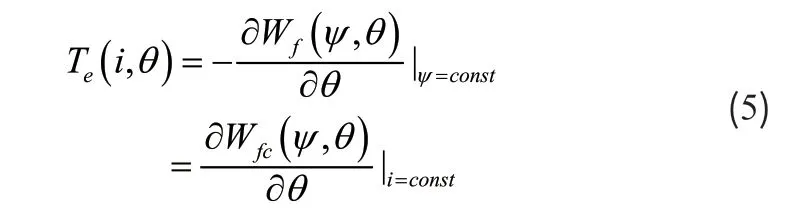
2 控制系统设计

■2.1 自抗扰控制的基本原理

自抗扰控制器(ADRC)是针对一类非线性不确定系统提出的一种非线性控制器，它是将现代控制理论对控制系统的认识和现代信号处理技术相结合，并汲取经典PID算法精华而构造的新型控制器[9]。

以二阶系统为例，ADRC组成如图2所示。

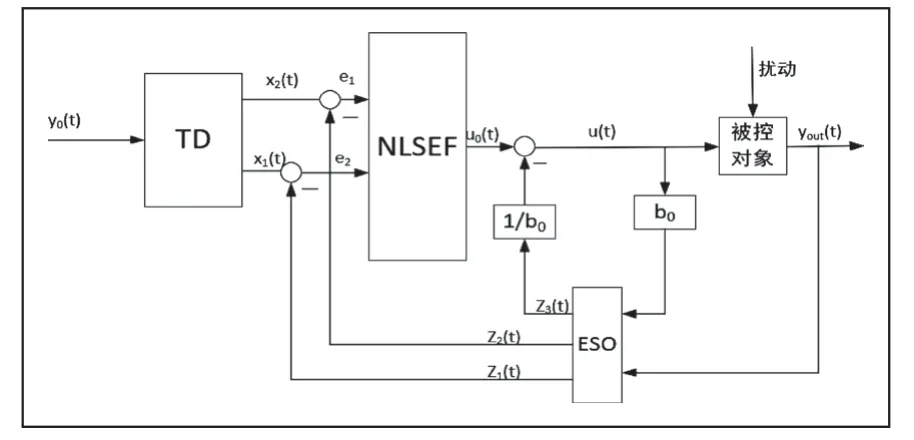
图2 自抗扰控制器结构图

由图2可知，自抗扰控制器由跟踪微分（tracking differential,TD）器、非线性状态误差反馈（nonlinear state error feedback,NLSEF）器、扩张状态观测（expand state observer,ESO）器组成。跟踪微分器包括跟踪和微分两部分，跟踪表示安排过渡过程，使信号的变化存在一定的惯性，实现对输入信号的跟踪。微分环节主要作用是得到输入信号的各阶导数，得到信号的变化趋势。ESO的主要作用是对系统的状态和被控对象的不确定性及外部扰动进行估计。在NLSEF中，将传统PID中的“线性和”以“非线性组合”的方式进行替代，从而得到类非线性PID，以此提高系统的控制质量。

■2.2 转速环节中的ADRC

图1描述了SRM的调速系统，其中的速度环控制器可以使用ADRC。SRM的转矩方程如式（6）所示：

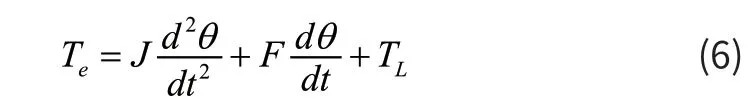
将式（6）进行变形可得：

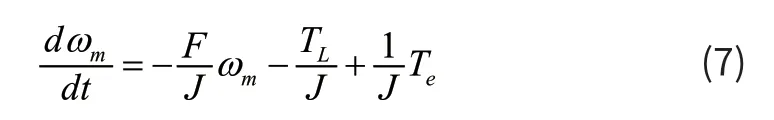
可进一步将式（7）转换成如下状态方程形：

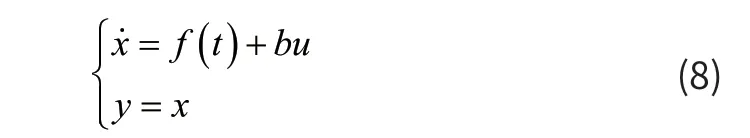
TD的形式为：

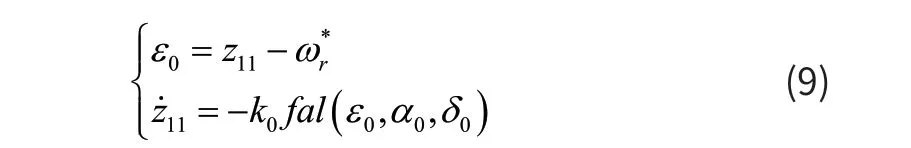
ESO的形式为：

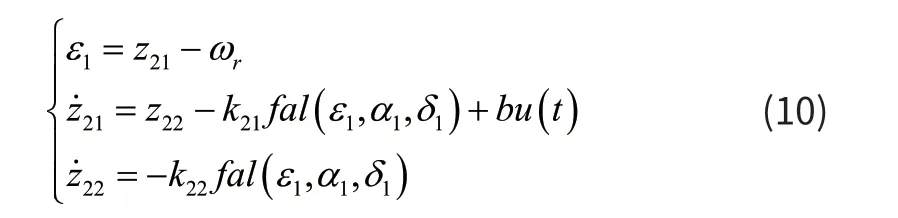
NLSEF的形式为：

函数fal如见式（7）：

由以上可知，对自抗扰控制器的参数，除了k21，k22，k3需要调试外，其它的控制器参数都可以设置成固定参数，选取e为10，α为0.1，δ为0.01。本文中采用混沌粒子群算法对以上参数进行优化。

■2.3 混沌粒子群算法

粒子群优化算法（Particle Swarm Optimization）源于对鸟群捕食行为的研究。粒子群优化算法的核心是利用群体中的个体对信息的共享而使得整个群体的运动在问题求解空间中产生给你从无序到有序的演化过程，从而获得问题的最优解。粒子群算法虽然简单，但是算法在迭代进化过程中存在的随机性不能保证例子能够收敛到全局最优位置，往往存在粒子过早陷入极值的现象。在粒子群中引入混沌模块可以丰富粒子种群的多样性、提高粒子全局搜索能力，形成混沌粒子群优化算法。在混沌粒子群不再重复经理空间的全部状态，克服了陷入局部最优的值的弱点，提高了优化算法的效率[9-11]。

在本文中，混沌粒子群优化算法中使用逻辑方程构造混沌序列：

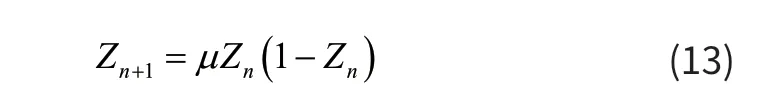
式中，μ—控制参数，当μ=4时处于完全混沌状态，对于任何初始值Z0，时间序列 Z0,Z1,… ,Zn都可以通过迭代计算确定。

将控制系统输出的转速差 e(t)绝对值的积分作为混沌粒子群算法的目标函数，也就是常用的绝对误差积分准则（IAE），即：

式中，t0为被控对象运行的时间，一般情况下，我们希望J越小越好。

本文需要调试的参数是ESO中的k21,k22和NLSEF中的，具体的寻优流程如下：

步骤1：初始化粒子群算法中的参数

步骤2：随机初始化粒子群中粒子的位置，这里的位置所表示的含义就是待整定的参数，计算每一个粒子的J值，并得到全局最小J值的粒子位置，称为全局最优位置，以及每个粒子的历史最优位置。

步骤3：迭代计算并更新粒子的当前位置和速度：

其中，下标k表示第k次迭代，i表示第i个粒子，d表示粒子的第d维，g表示全局最优值，V表示速度向量，P表示最优值向量，包括全局最优和历史最优，X表示位置向量， ω ,c1,r1,c2,r2表示权值，可调。

步骤4：将粒子混沌优化到所有的最佳位置，对于混沌变量所经历的每个个体最优解计算其适应度，根据适应度值得到全局最优位置并替换当前全局最优位置。

步骤5：当达到最大迭代时间或解决方案不再改变时停止搜索，否则返回到步骤3。

混沌粒子群自抗扰开关磁阻电机调速控制的原理图如图3所示。

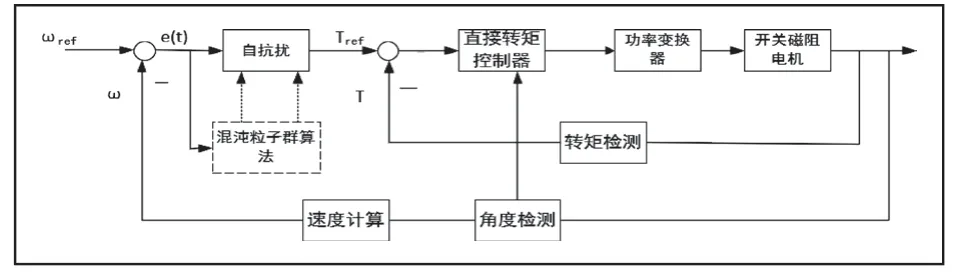
图3 整体控制原理图

3 仿真研究与分析

■3.1 仿真模型的建立

在Matlab上搭建仿真图，对控制效果进行仿真试验，验证基于混沌粒子群自抗扰控制器的性能与PID控制器的性能以及常用自抗扰控制器的性能的调速效果进行比较。

本次选用Matlab自带的6/4型开关磁阻电机，其中的主要参数：电阻值R=0.05Ω，转动惯量J=0.05kg·m·m，粘性阻力系数F=0.02N·m·s。选用的PI控制器Kp=2.3，KI=40，常规ADRC中k21=200，k22=10000，k3=100。选用的混沌粒子群的粒子群大小为20，迭代次数为50次。采样时间为0～0.5s。

■3.2 仿真结果

混沌粒子群算法的优化曲线如图4所示，最优个体适应值如图5所示，最优个体适应值越来越小，说明累计误差越来越小，算法在向较优的方向进行收敛，当进行到17次左右的时候，最优适应值以及各参数值基本不再变化，这里取beta1=6000，beta2=3343，K=1987作为CPSO_ADRC的参数。

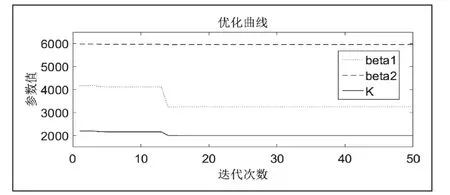
图4 混沌粒子群算法优化曲线

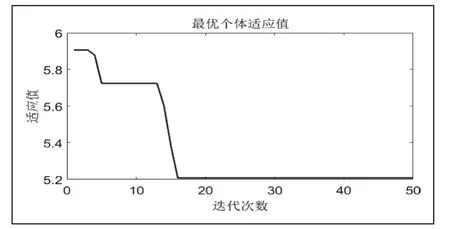
图5 混沌粒子群算法最优适应值曲线

将得到的CPSO_ADRC与传统PID控制器进行比较，设置启动速度为500r/min，启动负载转矩TL为8N·m，在t=0.25s时将转矩突变至15N·m，得到的结果如图6所示。

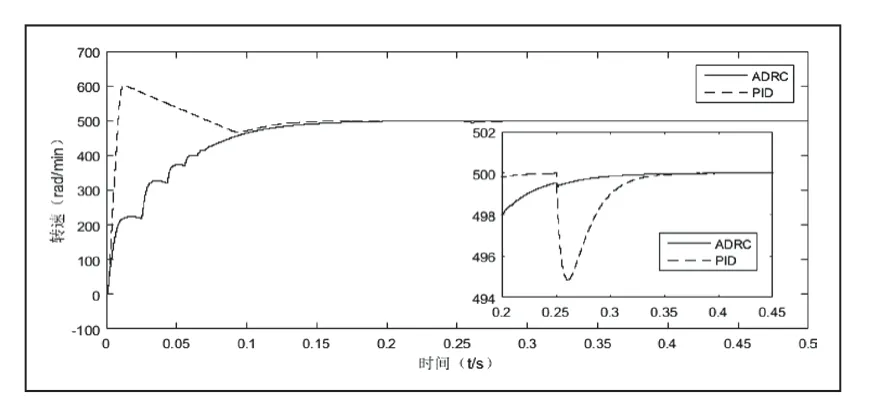
图6 CPSO_ADRC与PID对比图

显然，CPSO_ADRC控制器几乎没有超调现象产生，启动速度与PID控制器相当，都在t=0.1s左右处完成启动。在t=0.25s时转矩发生了突变，CPSO_ADRC几乎没有发生速度的变化，而PID控制器则从500r/min降落到了495r/min左右，说明CPSO_ADRC相比于PID有更强的抗干扰能力。

将得到的CPSO_ADRC与常规ADRC控制器进行比较，设置启动速度为500r/min，启动负载转矩TL为8N·m，在t=0.4s时将转矩突变至15N·m，得到的结果如图7所示。

图7 普通ADRC控制和CPSO_ADRC控制对比图

由上图可知，CPSO_ADRC在0.1s时就完成了启动，常规ADRC则需要到0.3s才能完成启动，说明CPSO_ADRC要比常规ADRC的启动速度快。在t=0.5S时转矩发生了突变，CPSO_ADRC几乎没有发生速度的变化，而常规ADRC控制器则从499r/min降落到了497r/min左右，说明CPSO_ADRC相比于常规ADRC有更强的抗干扰能力。

4 结束语

本文使用ADRC作为开关磁阻电机的速度环，利用混沌粒子群算法实现对ADRC的参数进行调整。这样即发挥了自抗扰控制不依赖被控对象精准模型的特点，又避开了其难以调整参数的弊端。通过对基于混沌粒子群自抗扰控制的开关磁阻电机模型进行仿真并与PID控制和普通自抗扰控制进行对比可知：这种控制策略有良好的静态和动态效果，并有较强的抗干扰能力。因此该种方法非常适合应用于开关磁阻电机这类非线性严重、扰动多的控制对象。