火星EDL过程动力学仿真平台

唐明章 王奇 黄伟 钱凯

火星EDL过程动力学仿真平台

唐明章1王奇1黄伟1钱凯2

（1 北京空间机电研究所，北京 100094）（2 北京东方创达软件有限公司，北京 100089)

“进入、减速、着陆（Entry，Descent，Landing，EDL）”火星的过程是实现整个火星探测任务最为重要的阶段之一，着陆成功与否直接决定探测任务的成败。文章对火星探测器自身气动减速阶段、降落伞弹射拉直阶段、降落伞开伞充气阶段、降落伞全张满减速阶段等EDL关键过程分别建立探测器进入段六自由度动力学模型、降落伞理想拉直过程动力学模型、降落伞开伞充气过程动力学模型、物伞及弹性吊挂组合系统着陆过程动力学模型。并在此基础上研制相应的动力学仿真软件模块，将各模块按照EDL过程进行集成，实现模块间数据传递，形成火星EDL全过程动力学仿真系统。最后对“火星探路者”EDL过程进行了动力学仿真分析，校验了系统的有效性和可行性。该平台可用于火星EDL全过程动力学性能的分析与预测。

火星探测 进入、减速、着陆动力学 仿真分析 软件设计

0 引言

2020年7月23日，我国首颗火星探测器“天问一号”发射升空。经历10个月太空之旅后，于2021年5月15日成功着陆火星乌托邦平原南部预选着陆区。

探测器从进入火星大气层至着陆主要经历三个阶段：大气进入段（Entry）、降落伞减速段（Descent）和着陆段（Landing），这三个阶段就是火星的“进入、减速、着陆（EDL）”过程。火星EDL过程是整个火星探测任务最为关键的环节[1-2]，着陆成功与否直接决定探测任务的成败。

整个火星EDL过程持续6～8min。此间探测器将经受严酷的峰值过载、峰值动压以及恶劣的气动加热环境的考验。另外，探测器进入初始状态参数和进入过程中火星复杂多变的环境参数直接影响探测器的着陆精度。因此对探测器和降落伞组成的物伞系统，在火星EDL过程中的动力学性能进行预测与分析有着非常重要的工程意义。文献[3-4]以“火星探路者”为研究对象，建立了物伞系统工作过程的动力学模型，系统地研究了舱伞系统减速下降过程的运动学特性和动力学特性。对于EDL全过程动力学的仿真研究，美国宇航局喷气推进实验室已开发专业仿真软件DSENDS[5-6]。国内，文献[7]对伞降过程中物伞系统建立了六自由度模型，并在此基础上对火星EDL过程进行了虚拟环境下的展示。文献[8]在降落伞减速阶段采用九自由度动力学模型，建立了火星EDL动力学集成仿真框架，实现了EDL过程的三维显示。

本文对物伞组合体着陆过程建立了精度更高的十二自由度动力学模型，同时对火星EDL其它关键过程分别建立了探测器进入段六自由度动力学模型、降落伞理想拉直过程动力学模型、降落伞开伞充气过程动力学模型。并开发相应的动力学仿真软件模块，将各模块集成实现EDL全过程动力学仿真集成软件。通过对“火星探路者”EDL过程的仿真分析验证了软件的有效性和可行性。

1 EDL过程动力学建模

1.1 进入段六自由度动力学模型

进入段从探测器进入火星大气层开始，到降落伞开伞时结束。进入段探测器受气动力和火星引力作用，探测器质心运动方程

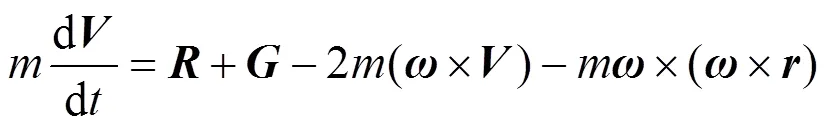
式中为探测器质量；为探测器速度；为时间；为火星地心至探测器质心的矢径；为火星自转角速度；为探测器气动力；为探测器所受火星引力。将式（1）中各矢量投影至航迹坐标系下即可建立进入段航迹坐标系下的质心动力学方程[9]。

在探测器坐标系下建立绕质心的转动方程[10]：

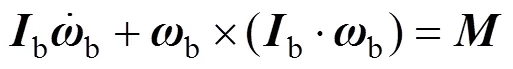
1.2 降落伞开伞过程动力学模型

降落伞拉直过程是由引导伞将折叠于伞包内的降落伞按序拉出的过程，也是降落伞开伞过程的第一步。本文采用Wolf[11]提出的理想拉直动力学模型：即在拉直过程中，伞衣和伞绳从伞包按序连续拉出，并且认为在拉直过程中回收物和引导伞遵循同一弹道倾角。

降落伞充气过程是指从伞系统全长拉直到伞衣第一次充满为止的整个工作过程。充气过程异常复杂，在很短时间内降落伞外形、质量分布等急剧变化。同时降落伞各部分力学特性也发生剧烈而复杂变化。目前尚无完整的理论模型对充气过程进行精确的计算和分析，通常采用经验模型来计算[12]。

1.3 物伞组合体着陆过程动力学模型

物伞系统是一个多体系统，动力学建模时可对物、伞分别建立刚体六自由度模型，形成十二自由度的组合系统。物伞之间由弹性吊带连接，通过平衡法可求得吊带系统在每个瞬时的约束力。

1.3.1 降落伞及探测器动力学模型

物伞组合体着陆过程中对降落伞模型做如下假设：

1）降落伞处于充满状态，且伞衣保持轴对称形状不变；

2）伞衣的压心与几何中心重合；

3）用附加质量表示降落伞非定常运动产生的流体附加力和附加力矩；

4）忽略尾流对降落伞的影响。

在降落伞坐标系建立六自由度运动方程如下所示

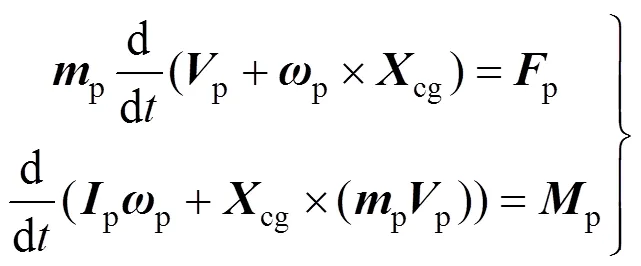
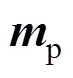
1.3.2 吊挂系统模型

降落伞与探测器之间通过弹性吊挂系统相连。图1为常用的两种吊挂连接方式，为伞绳交汇点，1、2、…、为吊挂系统与探测器连接点，下标为自然数。图1（b）吊挂中间有一个中间自由点，与伞绳交汇点由吊带连接。

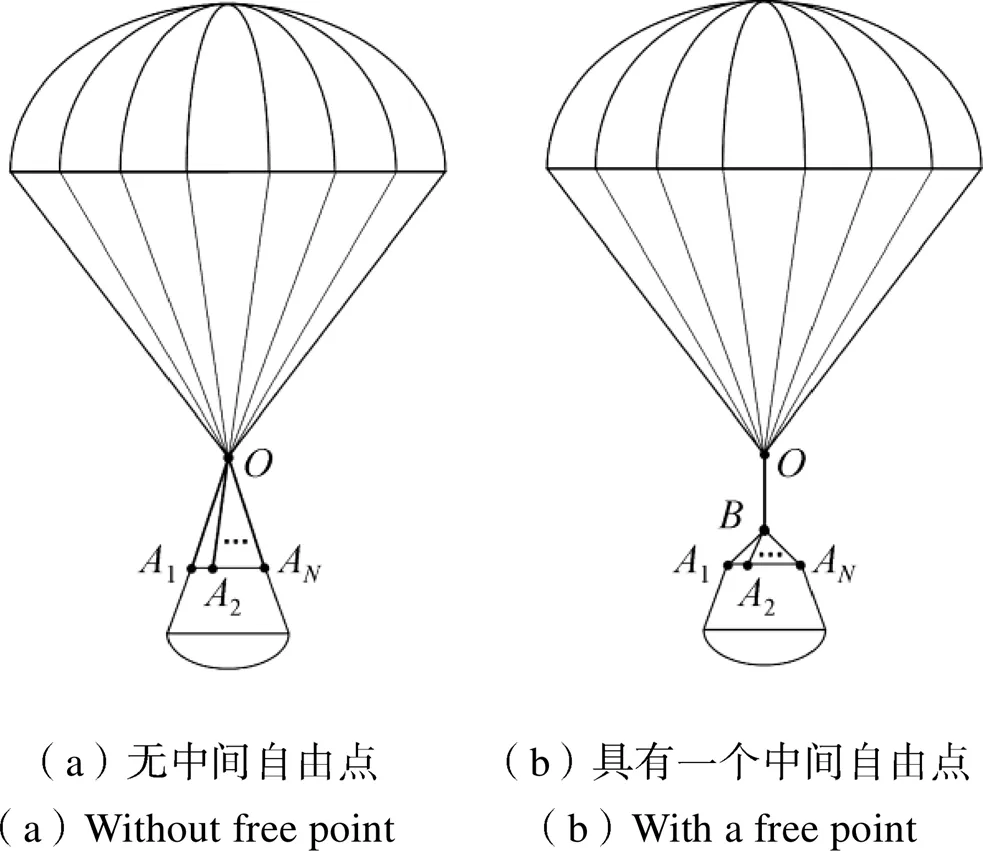
图1 吊挂结构示意

吊挂系统约束力的求解通常有小质量点法和“平衡法”两种方法。小质量点法将吊挂系统中间节点视为一个节点，由于中间节点质量很小，容易使运动方程出现刚性，严重限制了积分时间步长。故本文采用“平衡法”求解吊挂系统中伞绳、吊带、连接带的约束力。

1）对于无中间自由点的吊挂连接方式，在伞绳交汇点建立力的平衡方程

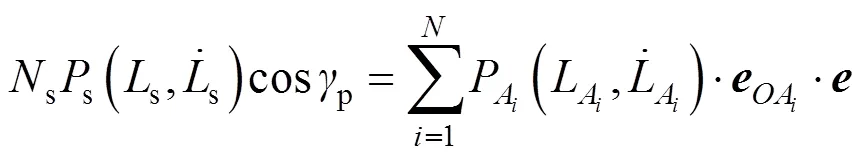
2）对于有中间自由点的吊挂结构，分别在和点建立平衡方程[15-16]

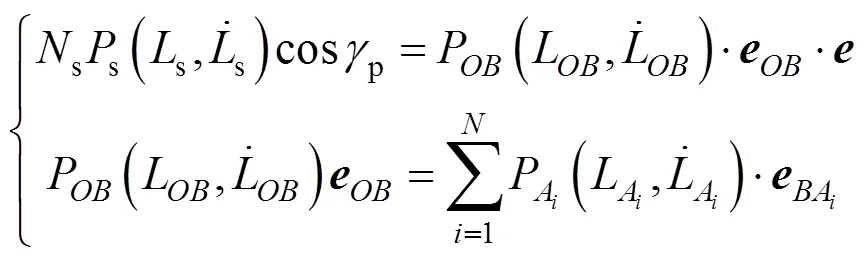
2 火星EDL动力学仿真系统设计

2.1 系统架构

系统总体架构采用三层架构设计，即界面层、业务逻辑层、数据访问层。

界面层指与用户交互的界面，用于接收用户输入的数据和显示处理后用户需要的数据。它包括进入段弹道计算参数输入界面、降落伞拉直及开伞过程计算界面、物伞着陆过程计算界面、动力学及运动学数值结果和时程曲线显示界面等等。

业务逻辑层是界面层和数据访问层之间的桥梁，实现业务逻辑。它包括进入段六自由度弹道分析、降落伞拉直及开伞充气过程动力学分析、物伞组合体着陆过程动力学分析及后处理模块。

数据访问层是实现对数据的增、删、改、查功能。将数据操作结果提交给业务逻辑层，同时保存业务逻辑层的数据。系统涉及数据包括：地球大气数据、火星大气数据、探测器模型数据、减速伞模型数据、探测器及降落伞气动数据、风场数据等等。

孩子的感冒与成人有所不同，这是他们的身体特点所决定的。小儿肺脾常不足，而心肝相对有余，所以感受外邪之后，也容易影响心肝脾的正常功能，造成感冒夹滞、夹惊、夹痰3种表现：

2.2 系统模块组成

依据EDL过程不同阶段将系统分为4个动力学仿真子模块及1个后处理模块，共5个子模块，如图 2所示。其中，4个动力学仿真模块为：再入六自由度动力学仿真模块、降落伞弹射拉直过程动力学仿真模块、降落伞充气过程动力学仿真模块、物伞组合体着陆过程动力学仿真模块。

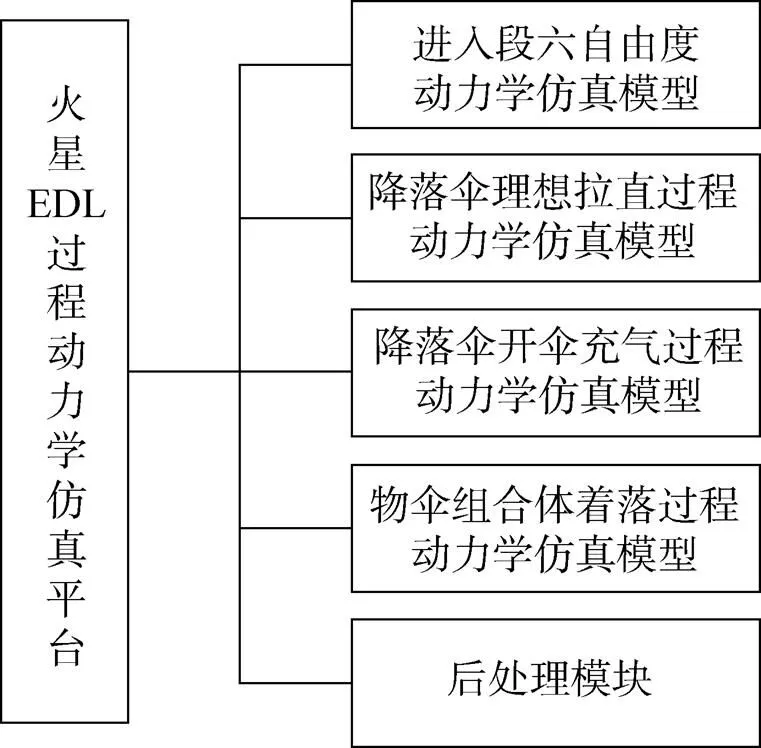
图2 系统模块组成

2.3 系统流程

系统流程如图3所示。首先给定探测器进入段初始状态参数：经度、纬度、高度、速度、飞行路径角、速度方位角、角速度、姿态角等。启动进入段六自由度动力学模块进行弹道积分计算，得到每一瞬时探测器的状态参数。当达到开伞条件时，停止当前模块的仿真任务。并启动下一个仿真模块，即调用降落伞弹射拉直过程动力学仿真模块进行仿真计算，仿真的初始状态参数从上一个模块的末端状态参数获取。其余模块的执行与此类似。

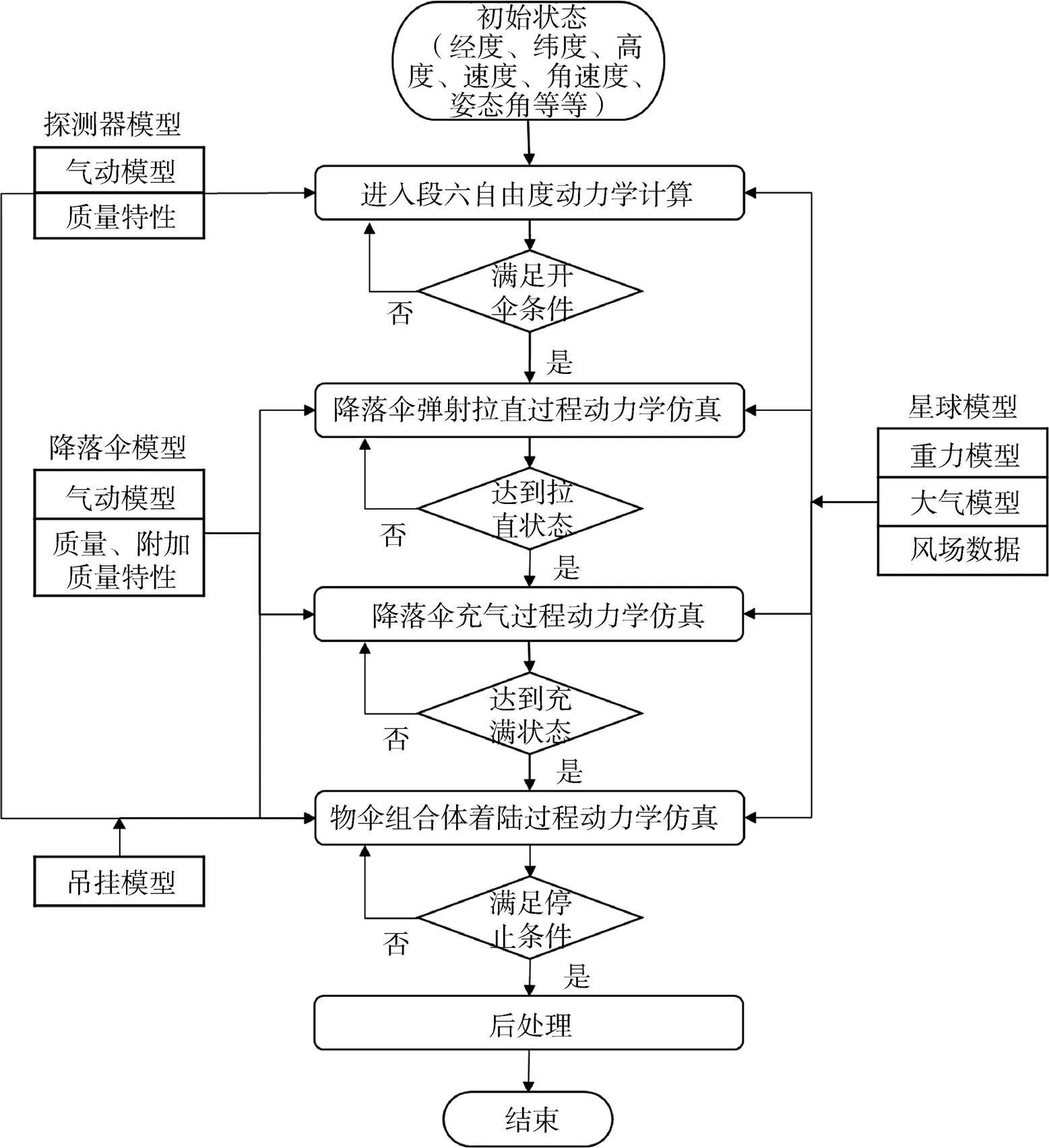
图3 系统流程及模块调用示意

动力学仿真模块执行中均需要调用星球模型：火星重力模型、大气模型、风场数据模型，以及飞行器模型。飞行器模型包括：气动模型、质量及附加质量特性模型。飞行器类型包括探测器、降落伞和物伞组合体三种，其中物伞组合体着陆动力学仿真模块还需调用吊挂模型。

3 “火星探路者”EDL过程仿真计算

3.1 进入段六自由度模块验证

以“火星探路者”探测器为研究对象，采用文献[17-19]数据对进入段六自由度模型进行验证。“火星探路者”气动性能数据来自文献[20]，仿真初始状态参数如表1所示。

表1 弹道初始条件

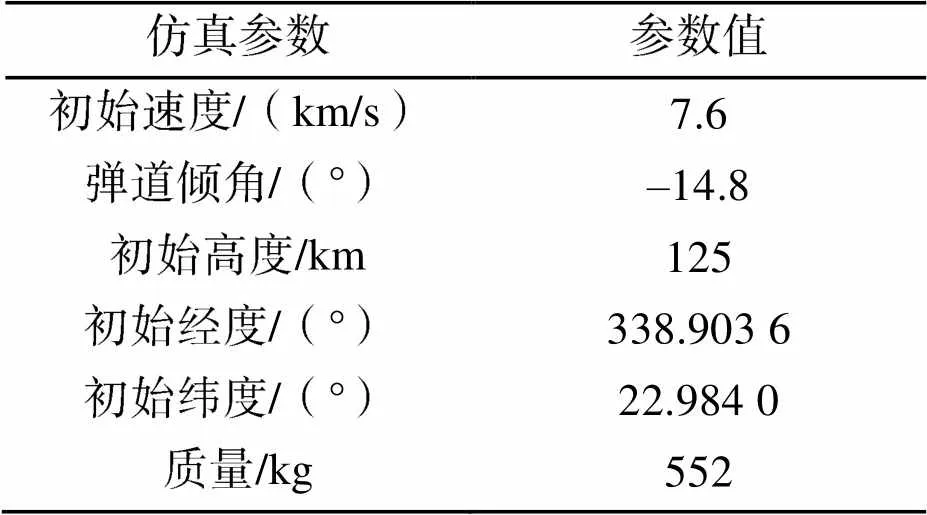
Tab.1 Initial conditions of trajectory

图4给出了探测器高度—速度变化关系与文献[18]仿真结果的对比，可以看到本文仿真结果与文献仿真结果一致。图4中，在60km高度以上，由于大气密度较低，气动减速不明显。主要减速段在60km高度以下。

3.2 物伞组合体动力学模块验证

物伞组合体模型由“火星探路者”号探测器、盘缝带伞和弹性吊挂组成，如图5所示，其中盘缝带伞参数见文献[21]，吊挂系统考虑有中间自由点和无中间自由点两种模型，连接带参数见文献[14]。

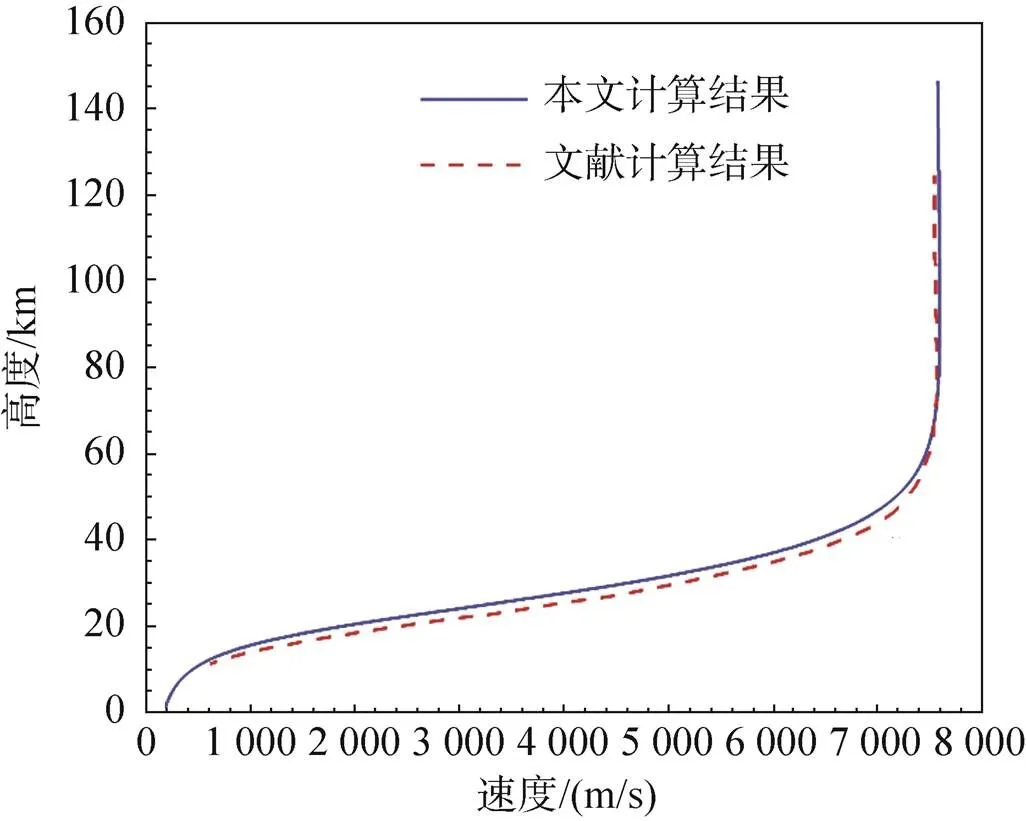
图4 进入段高度速度曲线

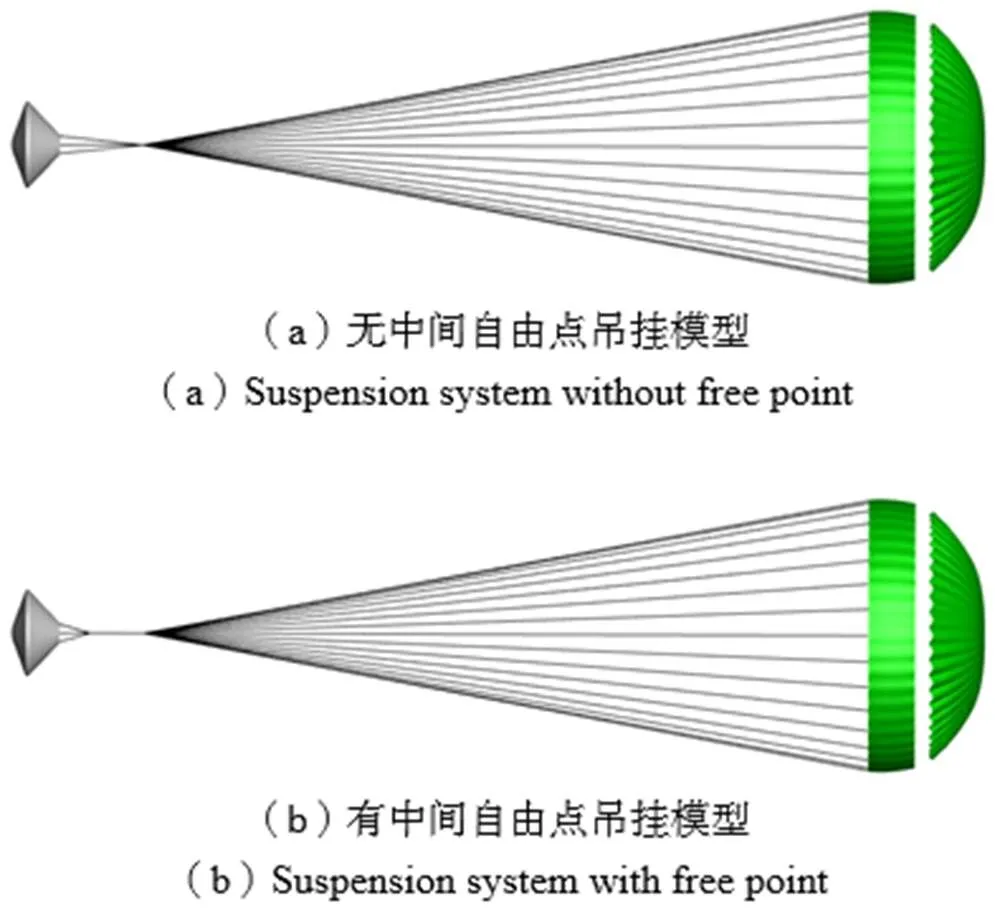
图5 物伞组合体及吊挂模型示意

本文以表2作为初始状态，进行物伞组合体动力学仿真计算，并与文献[21]结果进行对比验证。

表2 仿真初始条件

Tab.2 Initial conditions of simulation

文献[21]同时给出了计算结果和加速度计测量数据的处理结果。图 6为本文探测器高度随时间的变化计算结果与文献的对比，可以看到，本文仿真结果与文献仿真结果一致，但与文献中的测量数据存在一定的偏差。文献指出误差可能是由于仿真用的大气模型和火星实际大气参数存在一定的差异。另外，吊挂系统为物、伞之间的内部约束，不影响物伞系统整体运动。图 6中可以看到，两种吊挂模型下，探测器高度随时间变化曲线几乎是重合的。

图7为探测器下降速率随时间的变化。同样，由于吊挂系统为内部约束，图中两种吊挂模型对应的探测器垂直下降速率曲线几乎重合。在前10s，本文结果、文献结果、测量数据之间相差不大。10s之后出现较大的偏差，总体上垂直速度的计算结果要大于测量结果，这也与图6中高度仿真结果比测量结果下降更快相一致。与文献仿真结果的偏差可能是由于本文吊挂系统参数、降落伞结构和性能参数等与文献存在差别所致。

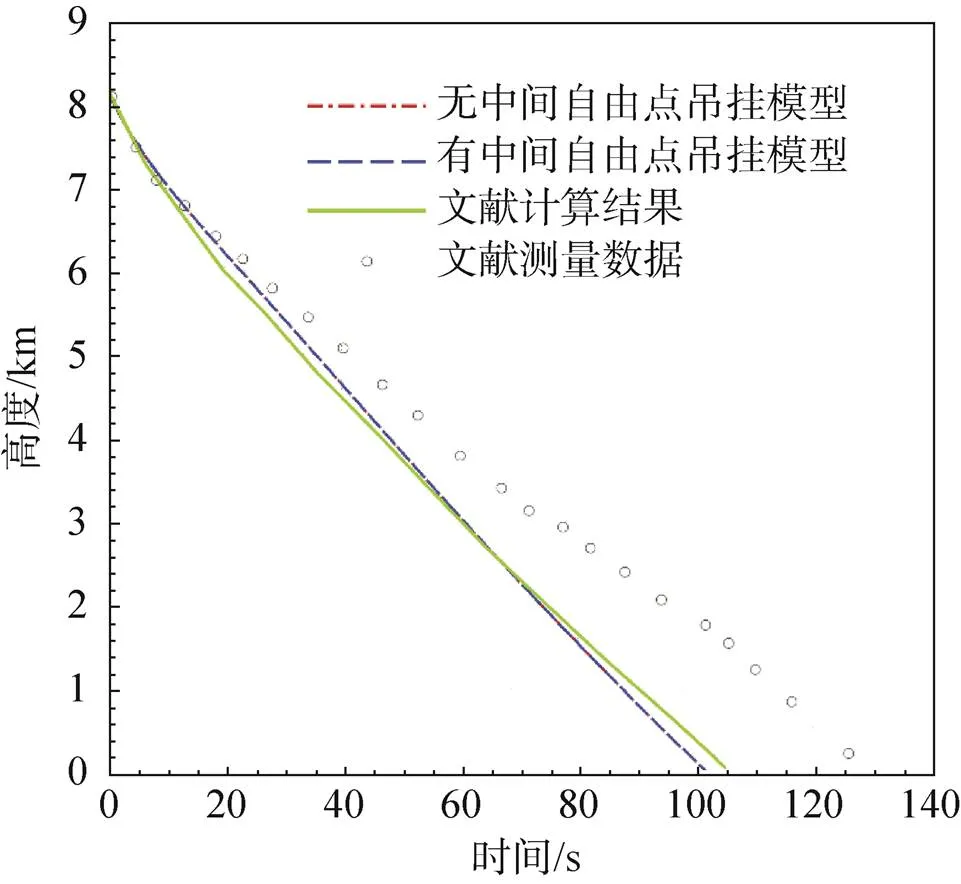
图6 探测器高度随时间的变化

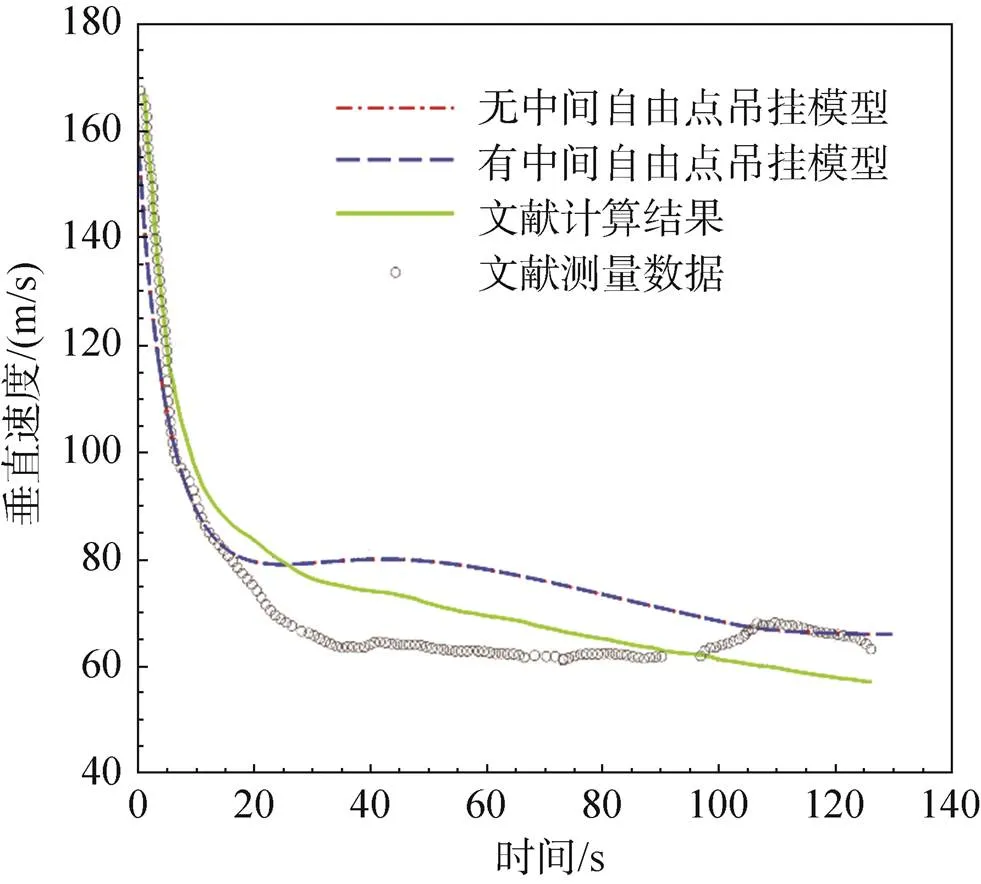
图7 探测器垂直下降速度随时间的变化

3.3 火星EDL全过程动力学仿真

进入段初始状态参数见表1。降落伞充气过程阻力面积随时间的变化参见文献[22]。物伞组合体模型与3.2节相同。

利用本文所建立的动力学模型，通过给定的进入段初始状态，可获得EDL全过程的动力学和运动学特性。其中图8为探测器高度随时间的变化关系。图9为探测器速度随时间的变化关系。两者变化趋势均与文献[18]一致。

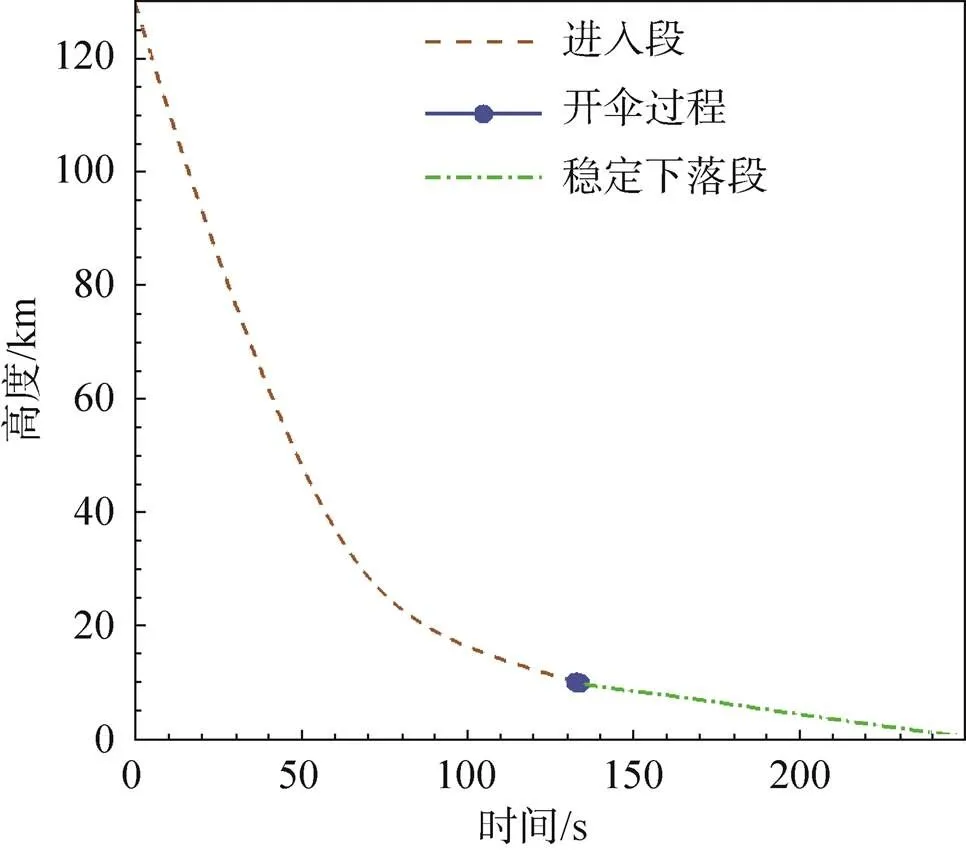
图8 高度随时间的变化

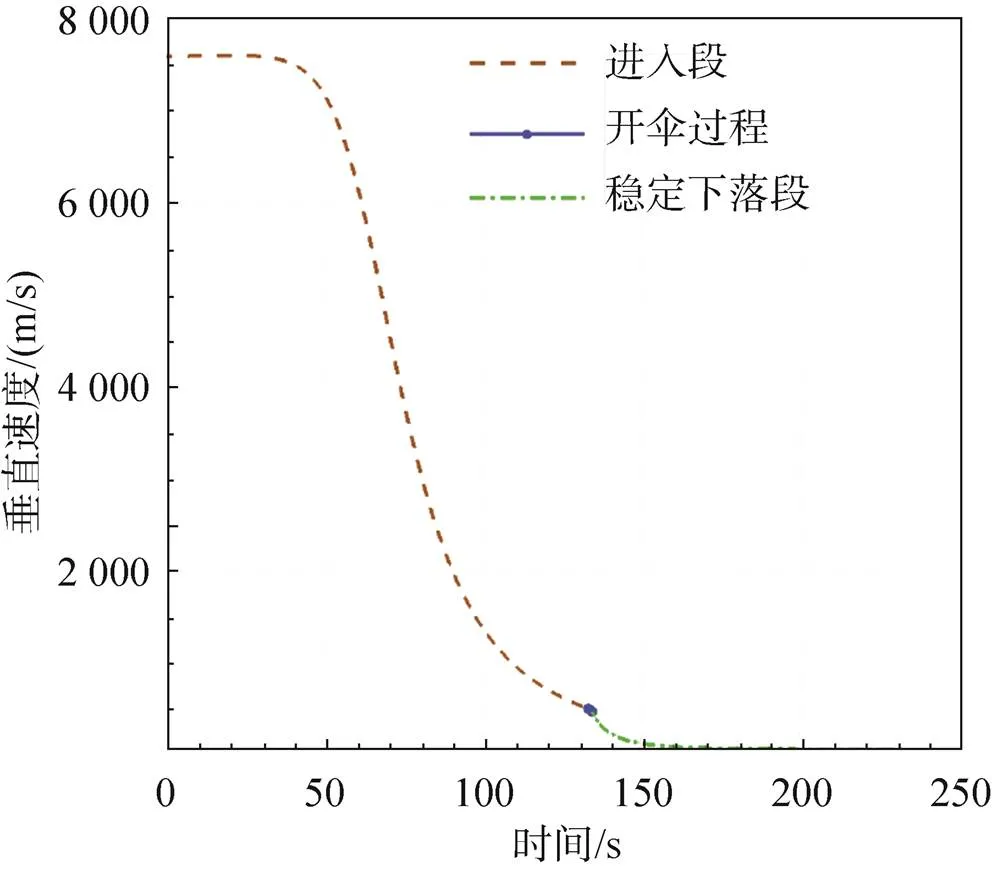
图9 速度随时间的变化

图10为探测器加速度随时间的变化关系。图中，最大过载在进入段69.4s，最大过载值为17.18n，对应的飞行速度为176.36m/s。这与文献[23]中最大过载17.3n，及对应飞行速度169.5m/s非常接近。另外，本文开伞过程最大过载8n，文献中开伞过程最大过载不到6n。这一差异可能是由于充气过程中阻力面积的变化与文献不同导致。

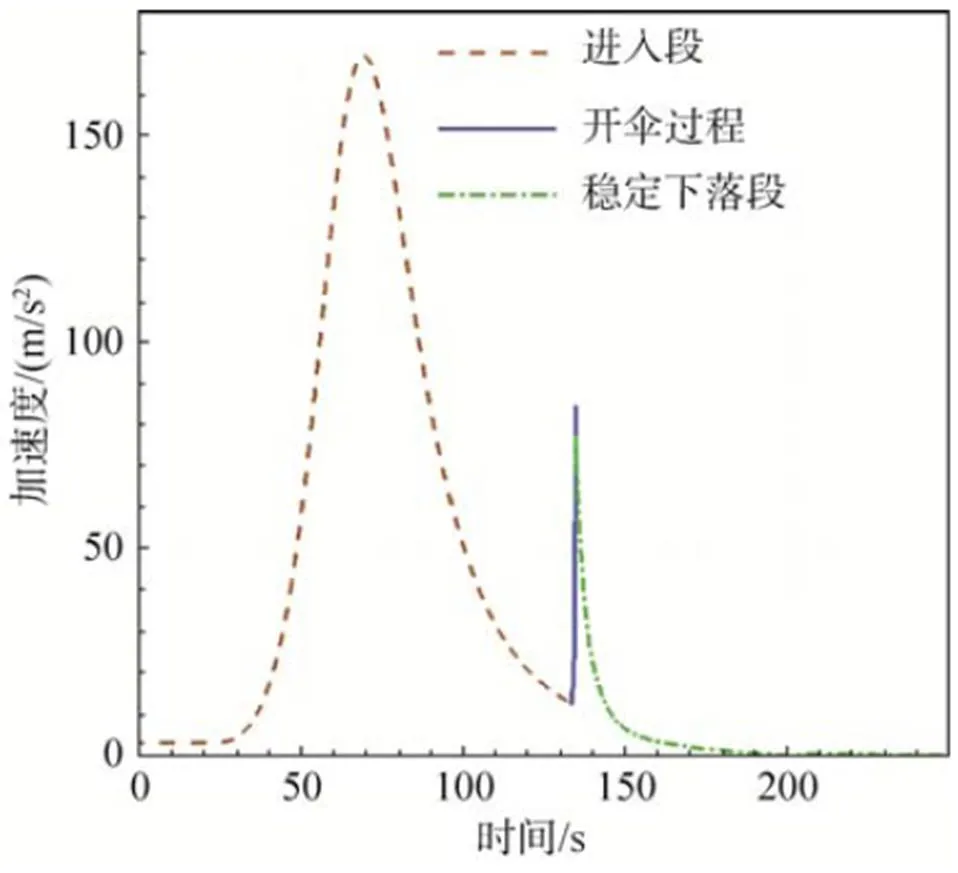
图10 加速度随时间的变化

以上分析表明，本文所开发的动力学集成软件可以对火星EDL全过程动力学特性进行有效地预测与分析。

4 结束语

本文对火星EDL过程不同阶段，分别建立了进入段六自由度动力学模型、降落伞拉直和充气过程动力学模型、物伞组合体着陆过程动力学模型。并开发了相应的动力学仿真软件模块，将各模块集成形成火星EDL全过程动力学仿真软件系统。通过对“火星探路者”和盘缝带伞组成的系统在火星EDL过程中的动力学特性进行仿真分析，验证了软件的有效性和可行性。

本文所研制动力学软件可用于火星EDL过程动力学特性的预测与分析。

[1] 饶伟, 孙泽洲, 孟林智, 等. 火星着陆探测任务关键环节技术途径分析[J]. 深空探测学报, 2016, 3(2): 121-128.

RAO Wei, SUN Zezhou, MENG Linzhi, et al. Analysis and Design for the Mars Entry, Descent and Landing Mission[J]. Journal of Deep Space Exploration, 2016, 3(2): 121-128. (in Chinese)

[2] BRAUN R D, MANNING R M. Mars Exploration Entry, Descent, and Landing Challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.

[3] 王海涛, 郭鹏, 程文科, 等. 伞舱系统在火星环境中的运动特性分析[J]. 航天返回与遥感, 2010, 31(1): 28-33.

WANG Haitao, GUO Peng, CHENG Wenke, et al. Analysis of Motion Characteristic of Parachute-vehicle System in Mars Environment[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(1): 28-33. (in Chinese)

[4] 鲁媛媛, 荣伟, 吴世通. “火星探路者”舱伞系统动力学特性仿真研究[J]. 中国空间科学技术, 2018, 38(2): 67-74.

LU Yuanyuan, RONG Wei, WU Shitong. Dynamic Characteristics Simulation Analysis for Parachute-vehicle System of Mars Pathfinder[J]. Chinese Space Science and Technology, 2018, 38(2): 67-74. (in Chinese)

[5] BALARAM J, AUSTIN R, BANERJEE P, et al. DSENDS a High-fidelity Dynamics and Spacecraft Simulator for Entry, Descent and Surface Landing[C]//IEEE Aerospace Conference, March 9-16, 2002, Big Sky, MT, USA.

[6] CAMERON J M, JAIN A, BURKHART P D, et al. DSENDS: Multi-mission Flight Dynamics Simulator for NASA Missions[C]//American Institute of Aeronautics and Astronautics AIAA SPACE, July 25-27, 2016, Long Beach, California, USA.

[7] 沈刚辉. 火星探测伞降段精确建模与EDL过程Unity3D仿真实现[D]. 北京: 北京理工大学, 2016.

SHEN Ganghui. The Precise Model of Parachute and Unity3D Simulation in Mars EDL[D]. Beijing: Beijing Institute of Thchnology, 2016. (in Chinese)

[8] 张青斌, 丰志伟, 马洋, 等. 火星EDL过程动力学建模与仿真[J]. 宇航学报, 2017, 38(5): 443-450.

ZHANG Qingbin, FENG Zhiwei, MA Yang, et al. Modeling and Simulation of Mars EDL Process[J]. Journal of Astronautics, 2017, 38(5): 443-450. (in Chinese)

[9] VINH N X. Optimal Trajectories in Atmospheric Flight[M]. New York: Elsevier Scientific Publishing Company, 1981.

[10] 赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997.

ZHAO Hanyuan. Reentry Dynamic and Guidance of Aircraft[M]. Changsha: National University of Defense Technology Press, 1997. (in Chinese)

[11] WOLF D . A Simplified Dynamics Model of Parachute Inflation[C]//American Institute of Aeronautics and Astronautics 4th Aerodynamic Deceleration Systems Conference , May 21-23, 1973, Palm Springs, CA, USA.

[12] 张青斌, 唐乾刚, 彭勇, 等. 飞船返回舱降落伞系统动力学[M]. 北京: 国防工业出版社, 2013.

ZHANG Qingbin, TANG Qiangang, PENG Yong, et al. Dynamics of Parachute-capsule Recovery System[M]. Beijing: National Defense Industry Press, 2013. (in Chinese)

[13] 熊菁, 秦小波, 程文科. 降落伞系统附加质量的研究[J]. 中国空间科学技术, 2002, 7(4): 32-38.

XIONG Jing, QIN Xiaobo, CHENG Wenke. The Added Mass Research in Parachute System[J]. Chinese Space Science and Technology, 2002, 7(4): 32-38. (in Chinese)

[14] 刘涛, 许望晶, 滕海山, 等. 射伞火箭开伞过程动力学仿真与分析[J]. 航天返回与遥感, 2020, 41(4): 45-54.

LIU Tao, XU Wangjing, TENG Haishan, et al. Dynamic Simulation and Analysis of Parachute Deployment Using a Propelling Rocket[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(4): 45-54. (in Chinese)

[15] 宋旭民, 彭勇, 程文科, 等. 一种新的吊挂系统建模方法[J]. 中国空间科学技术, 2005, 10(5): 57-61.

SONG Xumin, PENG Yong, CHENG Wenke, et al. A Novel Modeling Method of Suspension System[J]. Chinese Space Science and Technology, 2005, 10(5): 57-61. (in Chinese)

[16] 宋旭民, 秦子增, 程文科, 等. 具有倒“Y”型吊挂的降落伞系统动力学建模[J]. 国防科技大学学报, 2005, 27(5): 103-106.

SONG Xumin, QIN Zizeng, CHENG Wenke, et al. The Dynamic Model of a Parachute System with the Inverted “Y” Suspension[J]. Journal of National University of Defense Technology, 2005, 27(5): 103-106. (in Chinese)

[17] SPENCER D A, BLANCHARD R C, BRAUN R D. Mars Pathfinder Entry, Descent, and Landing Reconstruction[J]. Journal of Spacecraft and Rockets, 1999, 36(3): 357-367.

[18] BRAUN R D, POWELL R W, ENGELUND W C, et al. Mars Pathfinder Six Degree-of-freedom Entry Analysis[J]. Journal of Spacecraft and Rockets, 1995, 32(6): 670-676.

[19] DESAI P N, SCHOENENBERGER M, CHEATWOOD F M. Mars Exploration Rover Six-degree-of-freedom Entry Trajectory Analysis[J]. Spacecraft and Rockets, 2003, 43(5): 1-5.

[20] MOSS J N, BLANCHARD R C, WILMOTH R G, et al. Mars Pathfinder Rarefied Aerodynamics: Computations and Measurements[J]. Journal of Spacecraft and Rockets, 1999, 36(3): 330-339.

[21] WITKOWSKI A. Mars Pathfinder Parachute System Performance[C]//15th Aerodynamic Decelerator Systems Technology Conference, June 8-11, 1999, Toulouse, France.

[22] EDWARD J F. System Design Overview of the Mars Pathfinder Parachute Decelerator Sub System[C]//14th AIAA Aerodynamic Decelerator System Technology Conference, June3-5, 1997, San Francisco, CA, USA.

[23] DAVID A S, ROBERT D B. Mars Pathfinder Atmospheric Entry: Trajectory Design and Dispersion Analysis[J]. Journal of Spacecraft and Rockets, 1996, 33(5): 670-676.

Mars EDL Process Dynamic Simulation Platform

TANG Mingzhang1WANG Qi1HUANG Wei1QIAN Kai2

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Beijing Dongfang Chuangda Software Co., Ltd, Beijing 100089, China）

Mars EDL process is one of the most important stages in Mars exploration mission, whether the landing on Mars’s surface is successful, determines the success or failure of the mission. This paper concerns about the major dynamic phases in EDL process: entry, parachute deployment, parachute inflation and parachute-payload steady descent. The dynamic models are developed to describe the dynamic phases, which include entry 6-DOF dynamic model, parachute deployment and inflation dynamic model, multi-body dynamic model with elastic coupling. Correspondingly the computational modules based on dynamics are developed. The modules are integrated in sequence of EDL process, the data transfer between these modules is implemented. Finally, the integrated software system is used to simulate the dynamic of Mars Pathfinder’s EDL whole process. The results indicate that the software can be applied to effectively predict and analyze the dynamics of Mars EDL process.

Mars exploration; Entry, Descent, Landing (EDL) dynamics; simulation; software design

V11；V445

A

1009-8518(2021)03-0032-09

10.3969/j.issn.1009-8518.2021.03.004

2021-03-05

国家重大科技专项工程

唐明章, 王奇, 黄伟, 等. 火星EDL过程动力学仿真平台[J]. 航天返回与遥感, 2021, 42(3): 32-40. TANG Mingzhang, WANG Qi, HUANG Wei, et al. Mars EDL Process Dynamic Simulation Platform[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(3): 32-40. (in Chinese)

唐明章，男，1981年生，2006年获中国空间技术研究院飞行器设计专业工学硕士学位，高级工程师。研究方向为航天器进入，减速及着陆技术研究。E-mail：tangmz.cast@foxmail.com。

（编辑：陈艳霞）