固体废物腐蚀性测定（玻璃电极法）的不确定度分析

刘玮娜

摘 要：本文按照《固体废物 腐蚀性测定 玻璃电极法》（GB/T 15555.12—1995）中的方法测定固体废物的腐蚀性，并从测量重复性、天平称量、水的体积、标准缓冲溶液和pH计所带来的不确定度五方面分析其不确定度。经计算得知，对固体废物腐蚀性测定（pH值测定）的不确定度影响最大的是量筒和测量重复性。所以，在测定时可通过使用高精度的量筒以及增加平行试样的次数来降低标准不确定度。

关键词：固体废物;pH;不确定度

中图分类号：Z27文献标识码：A文章编号：1003-5168（2021）07-0028-03

Evaluation of Uncertainty in Solid Waste Glass Electrode Test（Method

of Corrosively）

LIU Weina

（Henan Zhengzhou Ecological Environment Testing Centre，Zhengzhou Henan 450000）

Abstract： In this paper， the corrosivity of solid waste was determined according to the method in Solid waste-Glass Electrode Test-Method of Corrosively （GB/T 15555.12—1995）， and the uncertainty was analyzed from five aspects： measurement repeatability， balance weighing， water volume， standard buffer solution and pH meter. The calculation shows that the most important influence on the uncertainty of solid waste pH determination is the measuring cylinger and the repeatability of measurement. Therefore， the standard uncertainty can be reduced by using a high precision measuring cylinger and increasing the number of parallel sampies.

Keywords： solid waste;pH;uncertainty

測量不确定度含义是指表征赋予被测量值分散性的非负参数[1]。每项检测过程中均会引入测定不确定度，为保证检测结果准确，需要核实数值的可接受性。测定的数据有效性与不确定度存在一定关系，因此，测定数据结论中要引入相关不确定度的数据分析[2]。

本分析报告中的实验按照《固体废物 腐蚀性测定 玻璃电极法》（GB/T 15555.12—1995）标准进行，测试了试样的腐蚀性，即pH值，并分析其不确定度。

1 方法原理及操作流程

1.1 原理

电池结构组成包括两部分：一是作为指示电极的玻璃电极，二是作为参比电极的饱和甘汞电极。在25 ℃条件下，氢离子活度变化10倍，电动势偏移59.16 mV。仪器直接显示pH数值。同时，pH计上有温度补偿装置，可以进行温度校正。仪器校准选用的标准缓冲溶液的pH值应与被测样品的pH值接近[3]。

1.2 操作流程

测定前，要进行仪器校准。选用与样品pH值相差≤2个单位的两个缓冲溶液进行校准。第一步，用第一个缓冲溶液检测后，取出电极，用装有无二氧化碳水的洗瓶冲洗干净，同时，用滤纸吸干水分。再浸入第二个缓冲溶液进行检测，当校核无问题时方可测定样品。

第二步，称取100 g样品，放入浸取用的容器中，用1 000 mL量筒量取1 000 mL无二氧化碳水，并加入容器中。再将其垂直固定在振荡器上，振荡频率设定为110次/min，振幅设定为40 mm，在室温下振荡8 h，静置16 h。经过滤装置进行固液分离，过滤后及时测定滤液的pH值。

第三步，将样品转移至洁净的烧杯中，放在磁力搅拌器上，烧杯中加入转子，将电极插入烧杯中，并以一定的速度缓慢搅拌使溶液均匀，最后等待读数稳定后记录样品pH值[3]。

2 建立数学模式

根据《固体废物 腐蚀性测定 玻璃电极法》（GB/T 15555.12—1995）实验方法原理，本篇论文中实验测定的pH值即为酸度计的仪器读数值。建立的数学模型如式（1）所示：

pH=pH仪器                             （1）

式中，pH为样品的pH值（实验测定的pH值是酸度计的仪器读数值）;pH仪器为酸度计测量多次测量的算数平均值。

3 结果与讨论

3.1 不确定度主要来源

按照数学模型和方法原理的要求，测量pH的不确定度由以下五部分构成：①测量重复性[U1];②天平称量引入的标准不确定度[U2];③1 000 mL量筒引入的标准不确定度[U3];④标准缓冲溶液引入的标准不确定度[U4];⑤pH计读数引入的标准不确定度[U5]。

3.2 测量重复性的不确定度

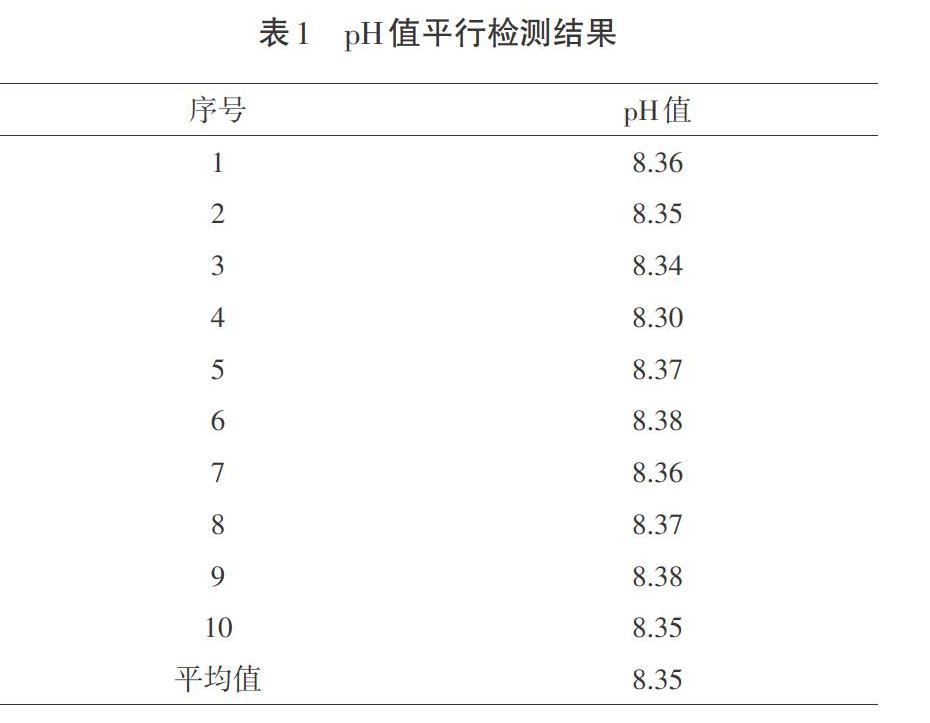
本次实验平行检测10次，分析重复性所引入的不确定度，检测结果如表1所示。重复性引入的标准不确定度为[Urep]，计算公式如式（2）所示[4]。

[Urep=i=1nxi-x2nn-1]=0.008                     （2）

式中：[xi]指测定的pH值;[x]指测定的pH平均值;[i]指测定次数;[n]指测定总次数。

自由度[V1]=10-1=9，重复性产生的相对标准不确定度为[U1]，计算公式如式（3）所示。

[U1=UreppH=0.001]                             （3）

3.3 天平称量的不确定度

3.3.1 分析天平校准产生的不确定度。实验采用天平的最大容许误差为±0.1 g，按照均匀分布模型，[K]=[3]，校准天平时引入的不确定度为[Um1]，计算公式如式（4）所示。

[Um1=2×0.132]=0.082 g                      （4）

3.3.2 分析天平分辨率产生的不确定度。实验采用的分析天平是数显式模式，分辨率为0.1 g，依据均匀分布模型，[K]=[3]，该项因素引入的不确定度为[Um2]，计算公式如式（5）所示。

[Um2=0.123]=0.029 g                           （5）

综合两项因素计算得出样品质量产生的不确定度[Um]，计算公式如式（6）所示。

[Um=0.0822+0.0292]=0.087 g              （6）

综上，样品质量引入的相对标准不确定度为[U2]，计算公式如式（7）所示。

[U2=U（m）m]=0.000 87 g                       （7）

3.4 水体积的不确定度

3.4.1 量筒校准引入的不确定度。用1 000 mL的量筒量取1 000 mL无二氧化碳水，容量误差为±5 mL[依据《常用玻璃量器》（JJG 196—2006）[5]]，根据均匀分布模型，[K]=[3]，因此，该项因素引入的不确定度为[Uv1]，计算公式如式（8）所示。

[Uv1=53]=2.89 mL                      （8）

3.4.2 温度对水体积的影响引入的不确定度。量筒的校准温度是20 ℃，倒入无二氧化碳水后，温度变化为±2 ℃，水的体积收缩系数为2.1×10-4，因此该项因素所引入的不确定度为[Uv2]，计算公式如式（9）所示。

[Uv2=1 000×2×2.1×10-43]=0.24 mL      （9）

综合两项因素计算得出水体积产生的不确定度为[Uv]，计算公式如式（10）所示。

[Uv=2.892+0.242]=2.90 mL                  （10）

綜上，影响水体积的各项因素带来的相对标准不确定度为[U3]，如式（11）所示。

[U3=U（v）v]=[2.901000]=0.002 9 mL                  （11）

3.5 缓冲溶液的不确定度

标准缓冲溶液不确定度的两项影响因素包括标准物质的纯度、容量瓶。容量瓶不确定度的影响因素包括校准、温度两部分。

3.5.1 标准物质纯度产生的不确定度。标准溶液的允差为±0.01pH，其自身纯度产生的不确定度为[Up]，计算公式如式（12）所示。

[Up=0.013]=0.005 8                        （12）

3.5.2 校准产生的不确定度。容量瓶规格为250 mL，经翻阅《常用玻璃量器》（JJG 196—2006）[5]，该规格的容量允差为±0.15 mL，按照均匀分布模型，[K]=[3]，则由该项因素引入的不确定度为[Uv1]，计算公式如式（13）所示。

[Uv1=0.153]=0.087 mL                    （13）

3.5.3 温度影响产生的不确定度。容量瓶的校准温度为20 ℃，倒入无二氧化碳水后，温度变化为±2 ℃，水的体积收缩系数为2.1×10-4，因此该项因素所产生的不确定度为[Uv2]，计算公式如式（14）所示。

[Uv2=250×2×2.1×10-43]=0.061 mL    （14）

综合两项因素计算得出容量瓶产生的不确定度为[Uv]，计算公式如式（15）所示。

[Uv=0.0872+0.0612]=0.11 m           （15）

综上，以上三项因素引入的相对不确定度为[U4]，计算公式如式（16）所示。

[U4=UPpH2+UVV2]=0.000 82         （16）

3.6 pH计的不确定度

3.6.1 pH计校准产生的不确定度。查阅检定证书，pH计的扩展不确定度是[U]（[k]=3）=0.01，因此，该项因素产生的不确定度为[UpH1]，计算公式如式（17）所示。

[UpH1=0.013]=0.003 3                   （17）

3.6.2 pH计分辨率产生的不确定度。实验采用的pH计分辨率为0.01，那么该项因素引入的不确定度为[UpH2]，计算公式如式（18）所示。

[UpH2=0.0123]=0.002 9                    （18）

则以上两项因素合成 pH计产生的不确定度为[UpH]，计算公式如式（19）所示。

[UpH=0.003 32+0.002 92]=0.004 4    （19）

综上，以上因素引入的相对标准不确定度为[U5]，计算公式如式（20）所示。

[U5=UpH14]=0.000 31                  （20）

3.7 合成相对标准不确定度

综上所述，合成相对标准不确定度如式（21）所示。

[U*pH/pH=U12+U22+U32+U42+U52=0.003 3]（21）

3.8 扩展不确定度[UpH]

取包含因子[k]=2（近似95%置信概率），则

[UpH=k×U*pH=2×0.003 3×8.35=0.06]  （22）

报告的扩展不确定度是根据合成标准不确定度乘以包含因子[k]=2得到，它达到的置信概率近似为95%。

4 结果表示

本实验条件下，归纳各不确定度，得到试样的pH值為8.35±0.06。其中，0.06为它的扩展不确定度，计算时使用的包含因子[k]为2，其给出了大约95%置信水平。不确定度各分量值如图1所示。

5 结论

为评估固废pH值测定的不确定度，主要研究了测量重复性、天平称量、水的体积、标准缓冲溶液和pH计所带来的不确定度。经计算得知，对固体废物腐蚀性测定（即pH值测定）的不确定度影响最大的是量筒和测量重复性。所以，在测定时可通过使用高精度的量筒以及增加平行试样的次数来降低标准不确定度。

参考文献：

[1]国家质量监督检疫检验总局.测量不确定度评定与表示：JJF 1059.1—2012[S].北京：中国标准出版社，2012.

[2]中国合格评定国家认可委员会.检验和校准实验能力认可准则：ISO/IEC17025：2017[S].北京：中国标准出版社，2018.

[3]国家环境保护局，国家技术监督局.固体废物 腐蚀性测定 玻璃电极法：GB/T 15555.12—1995[S].

[4]上海市计量测试技术研究院.常用测量不确定度评定方法及应用实例[M].北京：中国计量出版社，2001：45.

[5]国家质量监督检验检疫总局.常用玻璃量器：JJG 196—2006[S].北京：中国标准出版社，2006.