“工字型”平面不规则钢结构的弹塑性时程分析研究

石若利，李其伦

（云南大学建筑与规划学院，昆明 650500）

0 引言

钢材作为一种新型的建筑材料与混凝土相比主要表现在有以下几个优点：一是强度高，自身重量轻，抗震作用更好。二是钢铁材料的材质均匀，强度高，延展性强，钢材建筑的强度、刚度和稳定性容易达到要求，且密封性好。三是现场工人易于操作，步骤简单，许多组件可以在工厂预制完成，整体成本降低很多[1]。与传统的混凝土施工步骤相比，钢结构建筑省去了模板、拆模等工序，并且可以直接在工厂预制大部分构件，节省了人力资源和施工周期，降低了早期投资成本。四是钢材是一种循环利用的材料，不仅可以节约资源，还能更好地保护环境。

与传统的钢筋混凝土框架结构相比，钢结构同样具有重量轻、施工方便、节省资源等特点，钢结构房屋相比钢筋混凝土建筑有更灵活的布置，有更良好的延性和塑性变形性能。此外，钢结构还具有良好的抗震性能，提高了房屋的安全性[2]。由于不规则建筑的质量和刚度在水平方向上不是均匀分布的，在遭遇地震时结构刚度突变，在突变处的扭转现象目前已经得到了足够的重视和研究。李斌等[3]通过比较“工字型”平面不规则钢结构在多次地震波下的时程响应，验证了在试验中水平双向使用反应谱法计算公式的合理性。庄金钊等[4]通过对三种不规则钢框架结构在地震作用下的弹塑性分析，得到了不规则钢结构模型从三维转化为二维模型的方法。钱稼茹等[5]对位于北京商业中心的一些建筑的不规则钢筋混凝土框架模型进行了抗震试验研究，提出了不规则框架采用“强主柱弱主（次）梁、强次柱弱次梁、强主梁弱次柱”的抗震设计理念，对该框架进行弹塑性分析，提出适当提高主框架柱正截面承载力等抗震建议。以某俱乐部建筑为例，王玉华等[6]探讨了不规则框架结构的设计方法，阐述了结构体系、节点的计算分析结果和关键部位例如基础的设计[7]。为了研究平面不规则钢结构的抗震性能，以“工字型”钢框架为研究对象，对结构在3种不同地震波作用下进行了动力弹塑性时程分析，研究了结构的位移，包括顶层位移和最大层间位移，以及层间位移角和底部剪力，并对钢结构的薄弱环节进行分析，为研究抗震提供理论依据。

1 研究领域与方法

1.1 研究领域

运用弹塑性时程分析方法研究结构的抗震性能，根据美国太平洋地震研究中心（PEER）的介绍，选取了三种地震波，分别是El Centro波、Taft波和人工波，通过建立“工字型”平面不规则钢结构模型，对结构进行线性时程分析和非线性时程分析，研究其在三种地震波下的动力响应，评估结构的抗震性能。

动力弹塑性时程分析的内容包括结构的顶层位移、最大层间位移，以及层间位移角和底部剪力，并对钢结构的薄弱处进行分析。

1.2 模态分析法

模态分析法也叫振型叠加法，是一种常用的动力分析方法，它是动力分析的基础，包括反应谱分析和时程分析两种[8]。

三维地震运动的模态方程如下所示：

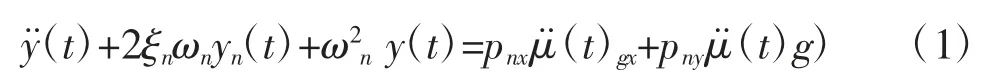
式（1）中，n是振型阶数。

1.3 反应谱分析法

反应谱方法有几个假设：结构是弹性反应，反应可以叠加；无土结的相互作用；质点的最大反应即为其最不利反应；地震是平稳随机过程，是一种拟静力方法。

其中单向水平地震响应，公式如下：

式（2）、（3）中，Sj为第j阶振型地震作用标准值效应，Sk为第k阶振型地震作用标准值效应，ρjk为固定阻尼的交叉模态系数，λT≤1.0。

双向地震作用的扭转效应，按照下列公式中的较大值确定：

1.4 时程分析法

时程分析法是对结构物的运动微分方程直接进行逐步积分求解的一种动力分析方法。由时程分析可得到各个质点随时间变化的位移、速度和加速度动力反应，进而计算构件内力和变形的时程变化。其在地震作用下运动方程为：

1.5 多遇地震下的弹性时程分析

从理论上讲，如果反映谱分析所用的反映谱是时程分析分析时用的地震波所产生的反映谱，而分析又限于弹性阶段，两者几乎没有差别，因为反映谱分析取足够的模态时只是忽略了影响很小的高阶效应；但是如果结构进入非弹性阶段，只有用时程分析。

反应谱分析法相比静力法在分析结构的地震响应方面有明显的优势，但这种方法实质还是一种拟静力方法，只能近似估算结构动力反应的最大值[9]。时程分析方法是一种相对比较精细的方法，不但可以考虑结构进入塑性后的内力重分布，而且可以记录结构响应的整个过程，计算结果更接近于结构真实动力响应。这种方法能反映出结构每一步的位移，速度和加速度，通过动力方程求解结构的基本响应。随着科技和计算机技术的不断发展，时程分析法的速度也大大提高，动力时程分析得到了更为广泛的发展和应用[10]。

2 数据处理

2.1 计算模型

本研究以一“工字型”钢建筑为研究对象建立有限元分析模型，建筑共16层，第1层层高4.5 m，其余层高均为4 m；本建筑的横向跨径和纵向跨径均为6 m；建筑总高度为60.5 m，抗震等级为二级，基本地震加速为0.10 g度，地震分组为第一组，场地为二类，特征周期为0.35 sec，且周期的折减系数为0.85。

主要的构件有：梁YB-H250×200×10×14，柱子设计支撑为YB-H350×300×12×18。下面是该结构的XY方向的平面图（图1）以及结构的3D图像（图2），结构截面尺寸（表1）。

表1 结构截面尺寸Table1 Section size of structure

运用ABAQUS有限元分析软件对钢框架模型进行抗震分析，得到其抗震的反应谱分析结果和时程分析结果，总结出其抗震规律[11]。

建立三维杆系模型，柱采用传统梁单元（B31），梁采用铁木辛柯梁单元（B32），考虑其横向剪切变形，梁柱通过节点几何连接成整体模型。该模型共有18 648个节点，12 060个单元，采用隐式算法对结构进行模拟计算，为了使计算结果更加精确，同时采用减缩积分对模型进行网格划分，最终得到的有限元模型如图1、图2所示。

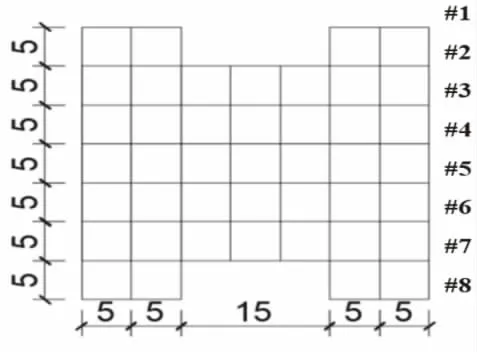
图1 结构平面图Fig.1 Structure plan

图2 有限元模型Fig.2 Finite element model

2.2 地震波的选取

结构时程分析一般要进行多遇地震下的线性分析和罕遇地震下的非线性时程分析，在进行时程分析前，应先选择合适的地震波是很重要的一步，在这里根据我们国家《建筑抗震设计规范》GB50011-2010的规定来选取地震波

地震波一般可以分为体波和面波，其中体波是我们经常需要考虑分析的。体波又可以分为二种类型，一种是横波，一种是纵波[12]。根据《建筑抗震设计规范》GB50011-2010，对于非常不规则结构，在进行完反应谱分析之后，一定要进行结构时程分析[13]。一般情况下要选用3组不同的地震波进行时程分析，有些特殊情况下要多选几组进行分析。在本研究中选取的是来自于美国太平洋地震研究中心（PEER）网站上的El Centro波、Taft波、人工波，这3种地震波的地震加速度记录分别如图3、图4、图5所示，这是为了更好地研究不规则钢框架结构的抗震性能，在综合考虑本建筑以及地震波选取原则的基础上[14]选取的。

图3 El Centro波Fig.3 El Centro wave

图4 Taft波Fig.4 Taft wave

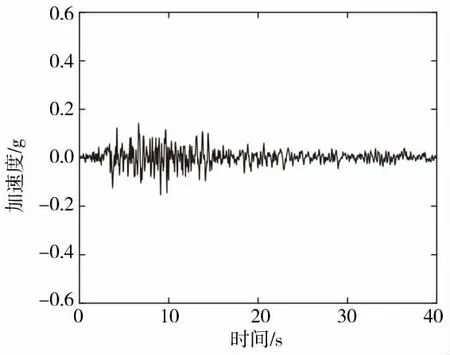
图5 人工波Fig.5 Artificial wave

3 结果

3.1 El Centro地震波下结构弹塑性时程分析

为了判断工字型平面结构的翼缘的平面扭转效应，研究了结构1层、8层、16层在1#、4#柱间El Centro地震波下的平面扭转的时程响应（图6），可以看出随着楼层的增高平面扭转角越来越大，但是即使16层的平面扭转幅度也是很小的，因此可以忽略工字型结构的平面扭转效应，取4#柱位置计算的最大弹性层间位移（如表2所示）。

表2 El Centro工字型结构最大弹性层间位移Table 2 Maximum elastic interlayer displacement of El Centro I-shaped structure

从表2可以看到，在El Centro地震波时程分析中，钢建筑模型在结构第三层的横向楼层位移最大，为12.2 mm。从三层到十六层，随着模型楼层的增大，横向层间位移逐渐减小，在十六层出现最小值为1.6 mm。建筑模型的层间位移角最大值出现在第三层到第五层，为0.0030 rad，当结构模型楼层随着从第五层到第十六层楼层数的增大，横向层间位移角逐渐减小，在十六层出现最小值为0.0004 mm。随着楼层数的增大，建筑模型的结构顶层位移逐渐增大，在结构第十六层达到最大值，为131.0 mm。通过表中数据，我们可以总结出在El Centro地震波时程分析下，钢建筑结构的层间位移角、横向层间位移、结构顶层位移随着楼层增加变化的趋势。同时结构模型的层间位移角、横向层间位移、结构顶层位移的最大值都小于国家规范《建筑抗震设计规范》GB50011-2010中规定的限值，满足要求[15]。

3.2 三种地震波下钢结构的模拟分析

从表2可以看到，在El Centro地震波时程分析中，钢建筑模型在结构第16层的结构顶端位移最大，为131.0 mm，第3、4、5层（共三层）的层间位移角最大，为0.0030 rad。El Centro波、Taft波、人工波三种地震波作用下的各楼层扭转角对比曲线如图6所示，从图中可以看出在在地震波作用下，时间第5sec左右，第16层的结构扭转角最大，随着时间的推移，结构的扭转角趋于稳定。

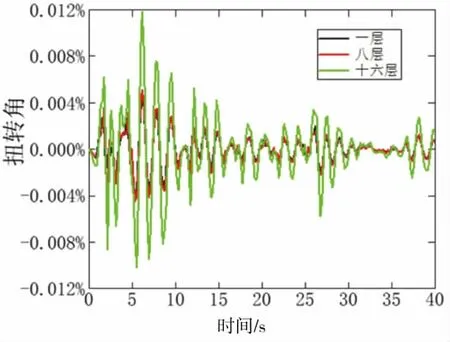
图6 楼层扭转角Fig.6 The torsion angle of the floor

从图7、图8可以看出，工字型平面不规则钢框架结构各层的最大位移随着地震震级的增强不断增大；在不同地震波下各层相对地面位移均随着楼层数的增高而增大，但是增长程度不同，人工波对结构的影响最大，El Centro波其次，Taft波影响最小；随着震级增强，各层位移也在增大，但都满足建筑抗震设计规范中关于多层钢架的最大弹性层间位移限值的要求[16]。在三种地震波作用下，最大层间位移都出现在了结构第3层，表明第3层为该建筑抗震的薄弱层。

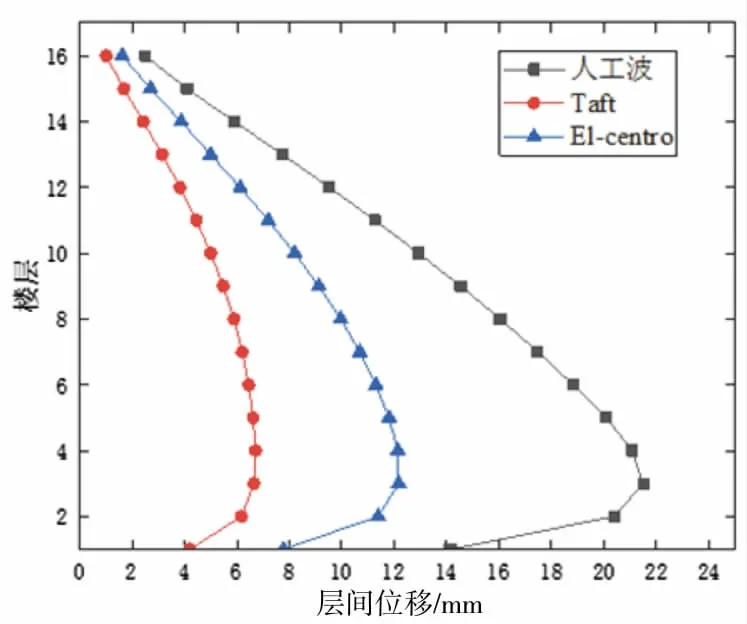
图7 不同地震波下各层层间位移对比曲线Fig.7 Comparison curves of interlayer displacements of each layer under different seismic waves

图8 不同地震波下各层相对地面位移对比曲线Fig.8 Comparison curve of relative ground displacement of each layer under different seismic waves

3种不同地震波作用下建筑结构的层间位移角变化规律如图9所示，从图可以看出，在第3、4、5层中结构的层间位移角相对最大，且最大值出现在第3层，所以第3、4、5层为该建筑结构的薄弱环层。3种不同地震波作用下建筑结构的基底剪力对比曲线如图10所示，从图可以看出，人工波对结构模型基底剪力的影响最大、ElCentro波其次，Taft波影响最小。随着时间的推移，三种地震波对结构的影响趋于稳定。从图9、图10综合来看，人工波对结构模型层间位移角和基底剪力的影响最大，El Centro波其次，Taft波影响最小。

图9 不同地震波下层间位移角Fig.9 Interlayer displacement angle under different seismic waves

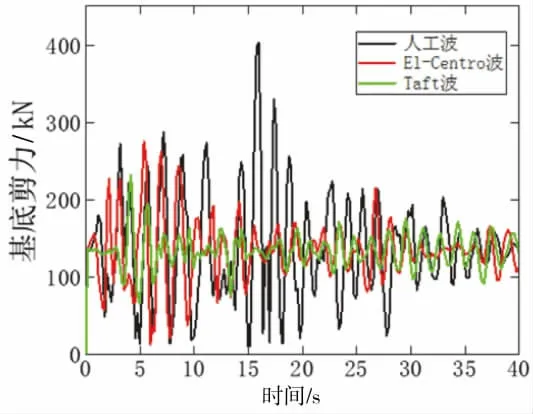
图10 不同地震波下基底剪力对比曲线Fig.10 Comparison curves of basement shear forces under different seismic waves

不同地震波下的弹塑性时程分析比较结果如表3所示。

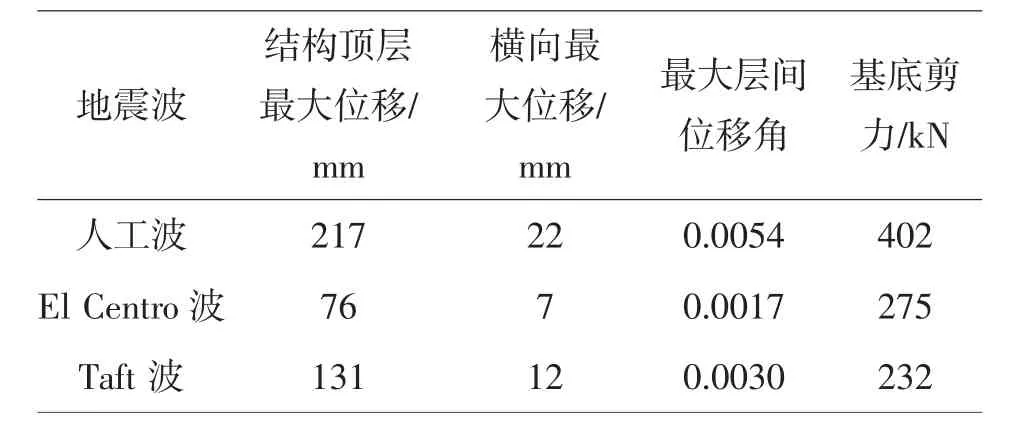
表3 不同地震波下的弹塑性时程分析比较Table 3 Comparison of elastoplastic time history analysis under different seismic waves

在人工波、El Centro波、Taft波对“工字型”平面不规则钢结构进行弹塑性时程分析中可以得出以下结论：随着地震震级的增强，结构各层的层间位移、位移角和各层剪力逐渐增大，且均满足我国规范《建筑抗震设计规范》GB50011-2010的要求。结构顶层最大位移之比为人工波：El Centro波：Taft波=2.8：1：1.7，结构最大层间位移角之比为人工波：El Centro波：Taft波=3.1∶1∶1.7，结构基底剪力之比为人工波：El Centro波：Taft波=1.71：1.17：1。在整个钢框架建筑结构中，第3、4层的层间位移和层间位移角均相对较大，故可以作为该“工字型”形平面不规则钢结构的薄弱部位，这为多层不规则钢框架结构的抗震设计与分析提供了借鉴[17]。

4 讨论

本文主要介绍了时程分析方法的原理和“工字型”平面不规则钢框架结构在三种地震波的作用下结构内部的地震响应的特征[18]。

通过对一栋总共有16层“工字型”的钢结构建筑进行时程分析得到如下的结论：

（1）“工字型”不规则钢结构具有较大的横向刚度和纵向刚度。从ABAQUS建模分析中获得的数据，可以看出该钢结构有些楼层层间位移和层间位移角会稍大，但仍满足规范要求。因为地震造成的建筑修复费用很高，甚至能达到建造费用的百分之八十[19]，而该钢结构的安全等级较高，在强震作用下发生受到严重损害或倒塌的概率较低，所以不论从安全角度还是经济角度，“工字型”不规则钢结构在抗震性能上都比较可靠。

（2）在地震作用下的非线性时程分析的结果均符合抗震规范要求[20]。在整个钢框架建筑结构中，第3、4层的层间位移和层间位移角相对较大，是“工字型”平面不规则钢结构的薄弱的地方，可以通过适当增加柱的截面尺寸或者增加配筋等方法提高柱的刚度。从总的分析结果来看该结构具有较大的刚度和良好的整体稳定性，结构进入弹塑性设计阶段后，符合结构对延性的要求。

5 结论

本文应用ABAQUS有限元分析软件建立了一个三维杆系模型对“工字型”平面不规则钢框架进行模拟，对钢框架结构在3种不同地震波（Elcentro波、兰州波、Taft波）作用下进行了动力弹塑性时程分析。通过对分析结果的对比，我们可以得到结论，结构模型在这3种地震波作用下产生的横纵楼层最大位移、最大层间位移角、最大基底剪力都较小，且都小于或等于国家规范《建筑抗震设计规范》GB50011-2010中的规定值，满足规范要求。这说明“工字型”平面不规则钢框架结构模型整体的刚度比较大，整体的抗震能力比较强。在3种地震波作用下，位于结构内部的地震响应存在一些差异，最明显的差异是结构模型在3种地震波作用下层间剪力随着楼层增加变化的趋势，其中结构模型受到El Centro波的影响最大，而受到Taft波的影响最小。建筑结构中柱的应力自下而上不断变化，在整个钢框架建筑结构中，第3、4层作为该“工字型”形平面不规则钢结构的薄弱部位，在实际工程中应当注意对薄弱部位进行抗震设计的加强。