基于机械比能理论的煤岩可钻性分级方法

谢志江，常 雪，杨 林，皮阳军

(1.重庆大学 机械工程学院，重庆 400044；2.重庆大学 机械传动国家重点实验室，重庆 400044；3.重庆大学 汽车工程学院，重庆 400044；4.中煤科工集团重庆研究院有限公司，重庆 400039)

瓦斯抽采是煤矿瓦斯灾害防治的主要技术手段，煤矿钻机是瓦斯抽采作业的关键技术装备，对于防治瓦斯灾害具有非常重要的意义[1]。现阶段，煤矿钻机的智能化程度还相对较低，在钻孔作业的过程中仍需要人工操作[2-3]。因此，提高煤矿钻机的自动化、智能化程度，实现钻进过程的自适应，是煤矿钻机的未来发展方向[4]。

煤岩地质信息在线识别是煤矿钻机自适应钻进的基础，也是实现钻孔作业无人化、自动化的先决条件。近年来，国内外诸多学者针对地层识别开展了深入的研究。S.S.Peng 等[5]提出一种通过监测钻压力变化来识别顶板锚固钻孔过程中空区和破碎区的方法。刘少伟等[6]、李鑫涛[7]研究发现，在顶板锚固孔施工过程中，不同的岩石类型会得到不同的动力响应，提出了依据推力、转速、钻进速度、扭矩等参数曲线的变化来获取所钻地层的分层信息。张幼振等[8]采用核模糊C 均值聚类算法对钻进过程中的钻压力、转速和钻进速度等参数进行训练，达到识别含煤地层岩性的目的。

综上所述，由于煤矿钻机钻孔施工过程中可采集的随钻参数十分有限，近年来的研究成果普遍采用钻进参数作为评价岩石可钻性的综合指标。然而Z.Q.Yue 等[9]通过实验发现，以钻进参数作为岩石可钻性的评价指标存在较大的随机性。因此，笔者提出一种以机械比能为分级指标，结合极限学习机的煤岩可钻性分级方法。同时，对钻进参数和机械比能这两种可钻性评价指标的分级准确率进行对比，来进一步检验所提方法的可行性与有效性。

1 分级指标及算法

1.1 机械比能

机械比能是岩石可钻性分级中最早使用的一项能量指标，最初主要用于地质钻探、石油钻井等领域中选择钻头和确定生产定额。经过几十年来诸多学者的不断优化和发展，机械比能在监测钻头工作状态、评估钻头工作效率、优化钻头结构等方面也发挥了重要的作用[10-11]。

1965 年，R.Teale[12-13]首次在岩石钻进中提出机械比能(Mechanical Specific Energy，MSE)的概念。其物理意义为单位时间内开挖单位体积岩石所需的功。定义式为：

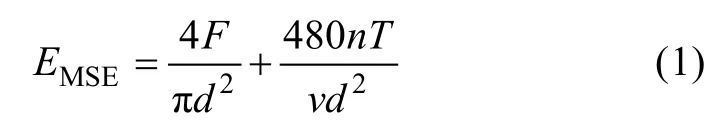
式中：EMSE为机械比能，GPa；F为钻压力，kN；d为钻头直径，mm；n为钻头转速，r/min；T为钻头扭矩，kN⋅m ；v为钻进速度，m/h。

1996 年，徐济银等[14]通过钻进实验得到了扭矩与钻压力之间的转换关系，如下式所示：

最后，结合以上两式就得到了计算更为方便的机械比能计算公式：

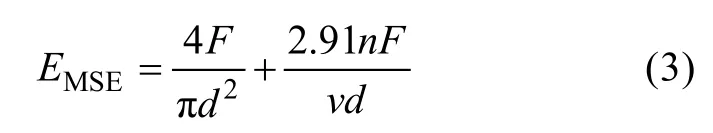
1.2 极限学习机

极限学习机(Extreme Learning Machine，ELM)是由南洋理工大学Huang Guangbin 等[15]于2006 年提出的一种新的单隐含层前馈型神经网络[16]。ELM的特点是在训练时随机选择输入层与隐含层之间的权值，在训练过程中仅改变隐含层与输出层之间的输出权值，缩短了调整网络结构参数的时间。除此之外，与传统神经网络的迭代训练过程所不同的是，ELM 将训练过程转化为线性方程组的求解，从而获得唯一的最优解[17]。大量学者的研究成果表明，ELM 的训练速度和泛化性能在单层前馈神经网络算法中均是最好的[18-20]。

该算法的主要原理如下：对于给定的训练数据集（{xi,ti）|xi∊R n,t i∊R m,i=1,…,N}和激励函数g(⋅)，ELM 算法可以简述为以下几个步骤：

①根据数据集的维数确定隐含层神经元的个数L：

式中：m、n分别为输出层和输入层的维数；a为[1,10]之间的常数；

② 随机产生权值和阈值（ai,bi）,i=1,2,…,N；

③根据选定的激励函数计算隐含层输出矩阵H；

④ 求解输出权值矩阵β=H↑⋅T；其中，H↑为H的Moore-Penrose 广义逆矩阵；T为输出矩阵。

2 PDC 钻头破岩仿真模型

研究瓦斯抽采钻孔施工过程中PDC 钻头与岩石之间的相互作用规律，可以采用钻进实验或计算机仿真来开展相应的研究工作。通过钻进实验可以得到较为可靠的结果，但实验研究无法观察到钻头破岩的微观过程。除此之外，为了研究钻进参数与岩石可钻性之间的相互作用规律，需要做大量重复性的破岩试验，时间周期较长，且破岩试验属于破坏性实验，需要耗费巨大的人力、物力，受实验设备和时间的限制，通过钻进实验所获取的数据往往十分有限。而计算机仿真则可以突破上述因素的限制，且具有很高的可重复性。基于此，本次采用ABAQUS 有限元分析软件建立PDC 钻头破岩仿真模型，对PDC 钻头破岩过程进行仿真分析。

2.1 基本假设条件

由于本文主要研究PDC 钻头破岩过程中钻进参数、机械比能与煤岩可钻性之间的相互关系，为便于分析，忽略部分次要因素，作如下假设：

①仿真中的煤及岩石材料为均质、各向同性；

② 由于PDC 钻头的硬度和强度远高于煤和岩石，故将钻头设置为刚体；

③岩石模型周围及底部属于井眼远场部分，地层为硬干地层，岩石孔隙压力为零。

2.2 材料强度准则及失效判据

采用Drucker-Prager 准则作为材料的强度准则，该准则是在Mohr-Coulomb 准则和Von-Mises 准则基础上扩展和推广而得[21]。

岩石失效的塑性应变判据为：

2.3 几何模型及材料参数

选取煤矿钻孔施工中常用的50ZTPN34 型三翼内凹PDC 钻头（图1a）参与仿真，由于钻头模型较复杂，故采用C3D10M 四面体单元进行网格划分。岩石模型（图1b）采用计算效率高、稳定性好的C3D8R 六面体单元进行网格划分，并采用沙漏控制和单元删除功能。

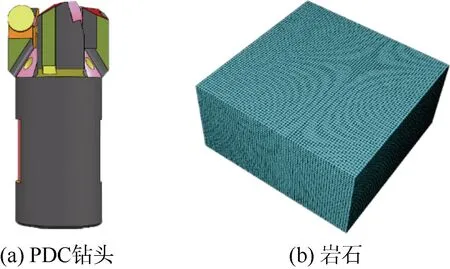
图1 钻头与岩石的三维模型Fig.1 3D model of PDC drill and rock

选取煤、泥岩、砂质泥岩和砂岩这4 种煤矿钻孔施工过程中最常见的材料参与仿真。部分材料参数见表1。

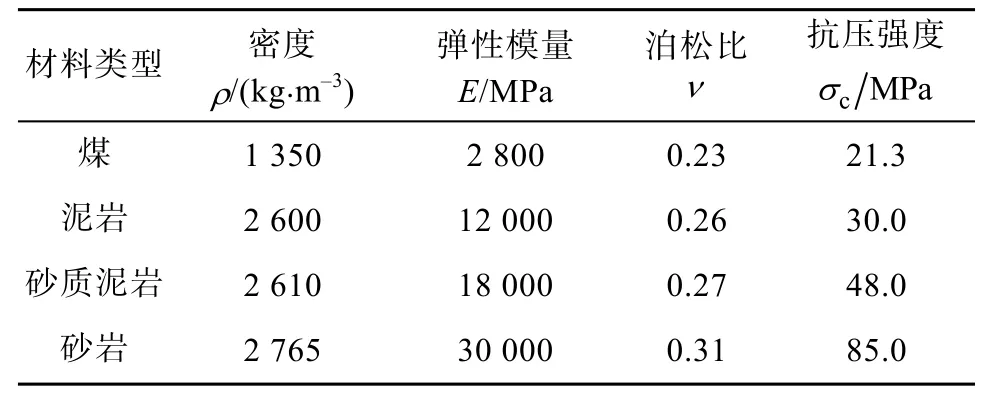
表1 仿真材料参数Table 1 Simulation material parameters

3 仿真结果及分析

在钻机和钻具相同的情况下，钻进速度和机械比能就仅与材料类型、钻头转速和钻压力有关。因此，本文将从材料类型、钻头转速和钻压力3 个方面研究钻进速度和机械比能的变化规律，并制定了如下仿真方案，共40 组仿真：

①研究材料类型、钻进参数与机械比能之间的变化规律。为避免仿真结果的偶然性，设定2 组钻进参数，分别钻进煤、泥岩、砂质泥岩和砂岩这4种材料，共8 组仿真。

② 研究钻头转速、钻进速度与机械比能之间的变化规律。固定钻压力，逐级改变钻头转速（60、80、100、120 r/min），分别钻进4 种材料，共16 组仿真。

③研究钻压力、钻进速度与机械比能之间的变化规律。固定钻头转速，逐级改变钻压力（5、10、15、20 kN），分别钻进4 种材料，共16 组仿真。

3.1 材料类型

设定2 组不同的钻进参数来分别钻进四种材料，其中，第一组钻进参数为：钻压力为5 kN、钻头转速为60 r/min。第二组钻进参数为：钻压力为10 kN、钻头转速为80 r/min，结果如图2—图4 所示。PDC 钻头只有在压入岩石一定深度后才能对岩石产生切削作用，因此，图2、图3 中线段A 之前为钻头压入岩石的过程，仔细观察可以发现，在这一阶段，钻头压入不同材料时的深度也有所差异，反映出抗压强度的不同。综合图2、图3 可知，钻头钻进不同材料时的位移–时间曲线呈现出不同的斜率，这反映出钻进速度的差异。由图4 可知，随着材料硬度的增加，钻进速度逐渐降低，机械比能逐渐增大。除此之外，当钻进参数相同时，不同材料的钻进速度和机械比能均有较大的区分度。当钻进参数不同时，不同材料的机械比能仍具有较高的区分度，但此时第二组钻进参数下钻进砂岩时的钻进速度与第一组钻进参数下钻进煤时的钻进速度较为接近，因此，仅以钻进速度作为可钻性评价指标可能会出现误判。

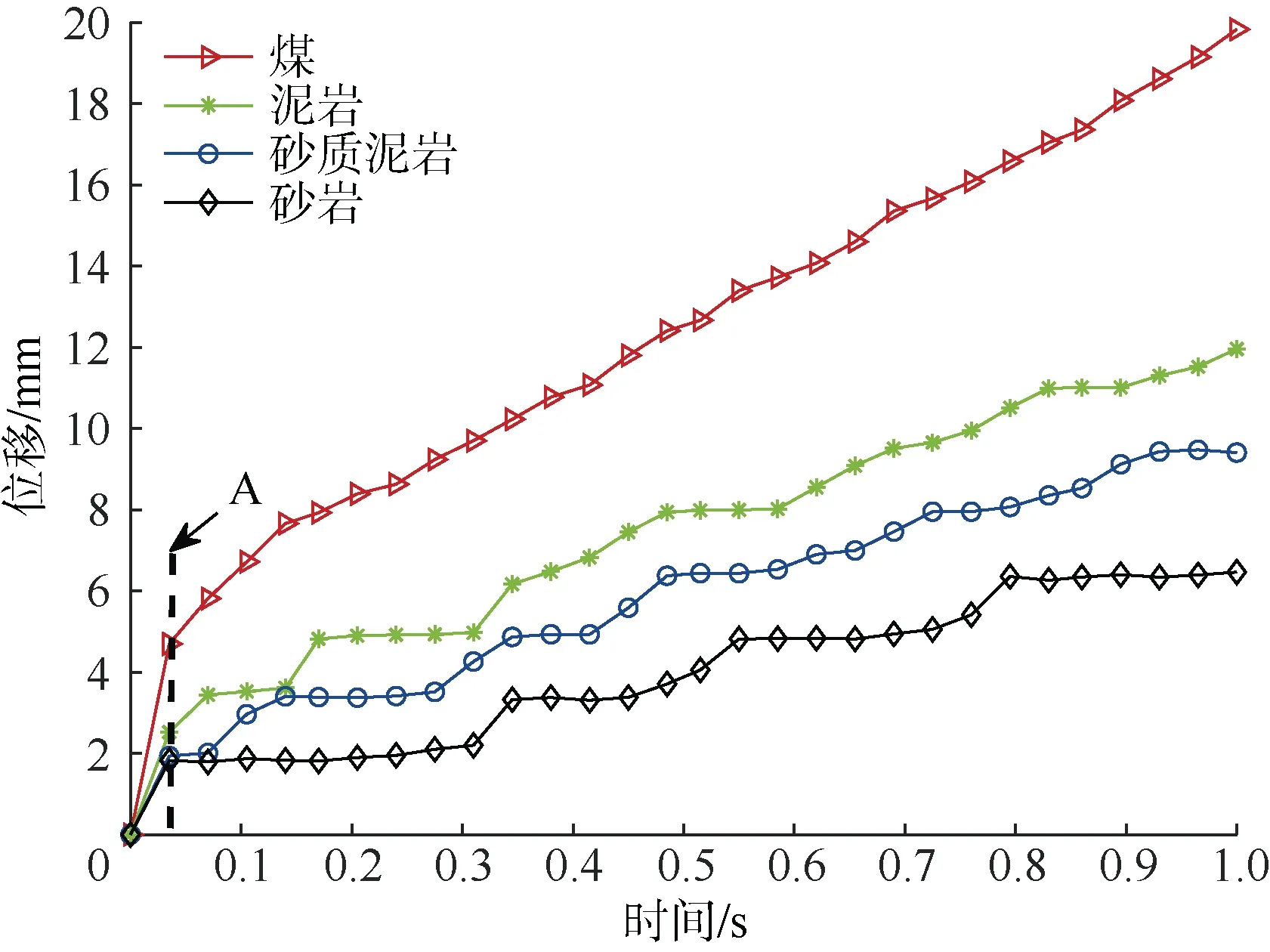
图2 第一组钻进参数下钻进不同材料的位移–时间曲线Fig.2 Displacement-time curves of drilling different materials under the first set of drilling parameters

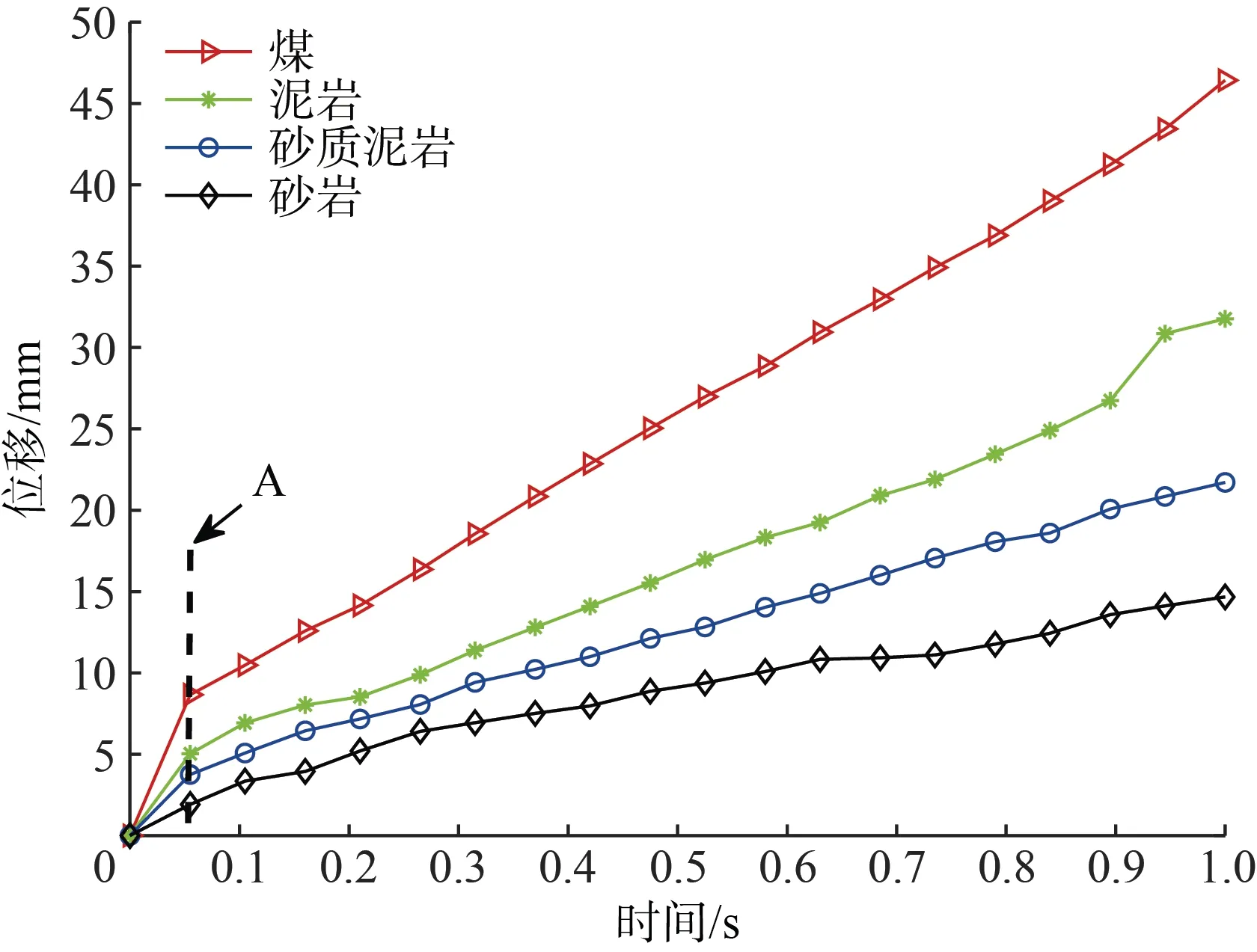
图3 第二组钻进参数下钻进不同材料的位移–时间曲线Fig.3 Displacement-time curves of drilling different materials under the second set of drilling parameters

图4 两组钻进参数下钻进不同材料时的钻进速度与机械比能Fig.4 Drilling speeds and MSE when drilling different materials under two sets of drilling parameters

3.2 钻头转速

固定钻压力为5 kN，逐级改变钻头转速，分别钻进4 种材料，仿真结果如下图所示。综合图5 中钻进4 种材料时的位移–时间曲线可知，由于岩石的硬度及破碎难度高于煤，因此，在钻进岩石时的位移–时间曲线中出现了“进尺台阶”现象[22]，且岩石越硬、钻头转速越低，该现象越明显，这一结果与马德坤[23]、林铁军等[24]的室内钻进实验结果相一致。由图6 可知，随着钻头转速的逐级递增，钻进速度也随之增大，但不同材料钻进速度的增长幅度不同，材料越硬，增长幅度越小。由图7 可知，钻头转速增大时机械比能也会随之升高，这是因为增加钻头转速虽然可以提高破岩效率，但也使得单位时间内摩擦所消耗的能量增加，最终引起机械比能的变化。

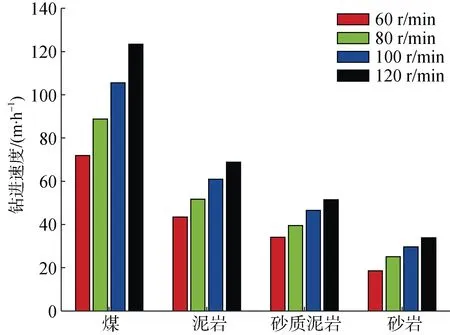
图6 不同转速下钻进4 种材料时的钻进速度Fig.6 Drilling speeds when drilling four materials at different rotation speeds

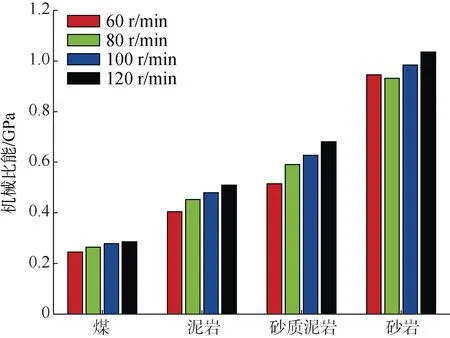
图7 不同转速下钻进4 种材料时的机械比能Fig.7 MSE when drilling four materials at different rotation speeds

3.3 钻压力

固定钻头转速为60 r/min，逐级改变钻压力，分别钻进4 种材料，仿真结果如下图所示。由图8可知，随着钻压力的增大，钻头钻进不同材料时的位移–时间曲线逐渐趋于平滑，“进尺台阶”现象也逐渐减弱。由图9 可知，随着钻压力的增大，钻进速度也不断增大，因此，在排屑状况良好的情况下，增大钻压力可以提高钻孔效率。由图10 可知，对于煤及泥岩、砂质泥岩等较软的岩石，当增大钻压力时，机械比能会有略微增大并最终稳定在一定范围内，这是由于钻压力增大时，虽然会使钻头与岩石之间的摩擦力增大，但也使钻头与岩石之间的接触更紧密，从而提高破岩效率。但对于较硬的岩石，如砂岩，当钻压力增大时，机械比能会逐渐降低，结合钻进砂岩时的位移—时间曲线可知，在钻压力较小时，钻头仅在岩石表面刮切了极小的一层，无法高效破岩。当钻压力增大时，钻头与岩石之间的接触状况得到改善，破岩效率得到了提高，机械比能也逐渐降低。因此，在钻进硬岩时需要设置较大的钻压力。

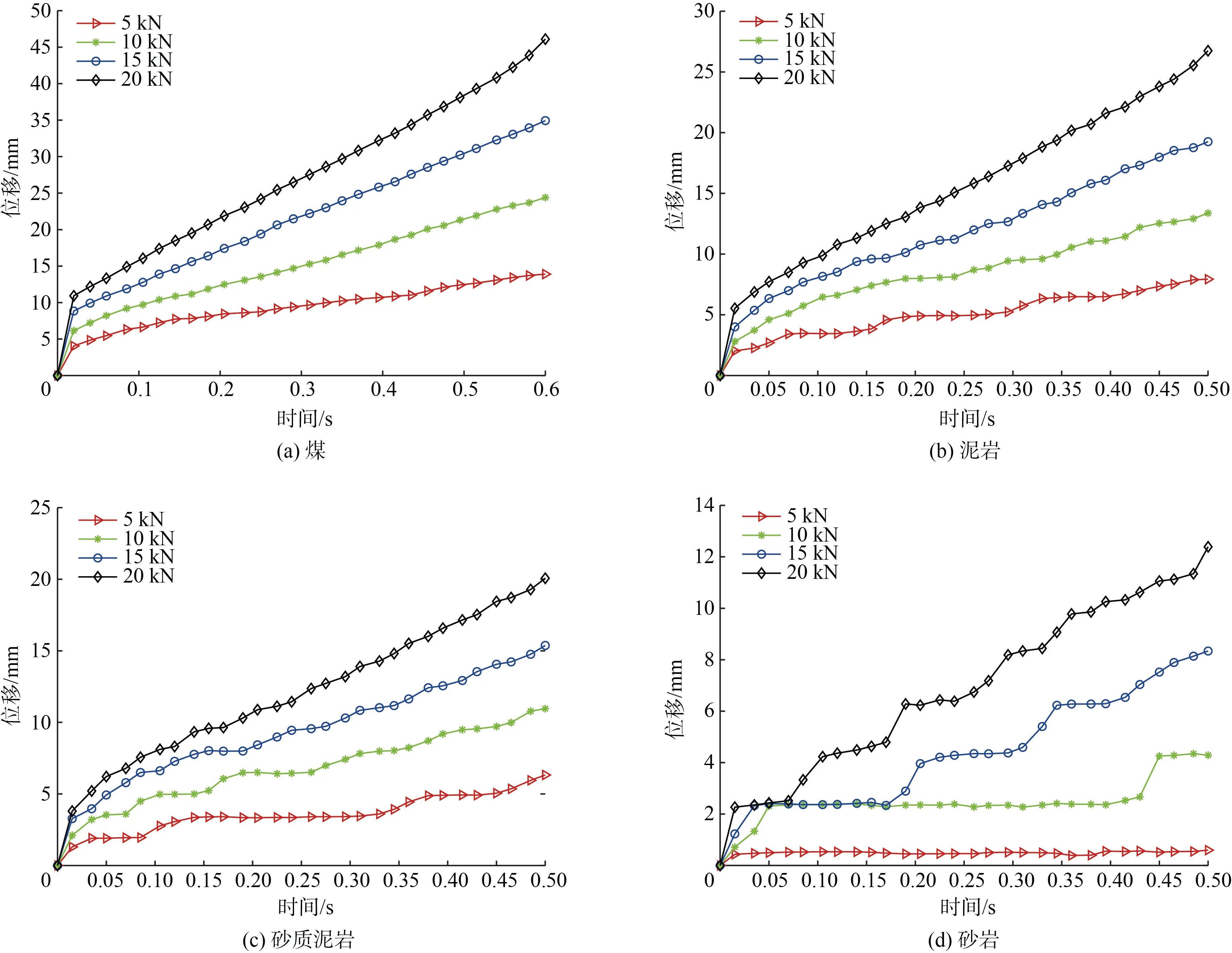
图8 不同钻压力钻进不同材料时的位移–时间曲线Fig.8 Displacement-time curves when drilling sandstone under different drilling pressures

图9 不同钻压力下钻进4 种材料时的钻进速度Fig.9 Drilling speeds when drilling four materials under different drilling pressures

图10 不同钻压力下钻进4 种材料时的机械比能Fig.10 MSE when drilling four materials under different drilling pressures

4 基于ELM 的煤岩可钻性分级

通过ABAQUS 仿真，共获得40 组包含钻压力、钻头转速、钻进速度等钻进参数和机械比能的PDC 钻头破岩仿真数据，限于篇幅，仅列出部分数据(表2)。依据破碎的难易程度将煤和岩石的可钻性分为4 级，其中煤属于1 级，砂岩属于4 级，即破碎难度越大，可钻性级别越高。

为了对比钻进参数和机械比能这两种可钻性指标的分级准确率，分别将表2 中钻进参数和机械比能作为样本输入 ELM，以可钻性等级作为输出。在MATLAB 中，随机抽取表2 中20 组数据作为训练样本，并将全部数据作为测试样本。同时为避免分级结果的偶然性，在同一台电脑上分别对2 个不同输入层的ELM 神经网络算法运行10 次，记录每次的分级准确率及运行时长。由图11 可知，对于同一种神经网络算法，以机械比能作为煤岩可钻性分级指标时的分级准确率保持在90%以上，远高于以钻进参数作为可钻性分级指标时的准确率，这是由于钻压力、钻头转速和钻进速度这3 个钻进参数与煤岩可钻性之间的映射关系并不唯一，存在较大的随机性。对于同一种神经网络算法，当采用不同的输入数据时，其运行时间无明显差异。

图11 分级准确率与运行时间Fig.11 Classification accuracy and running time

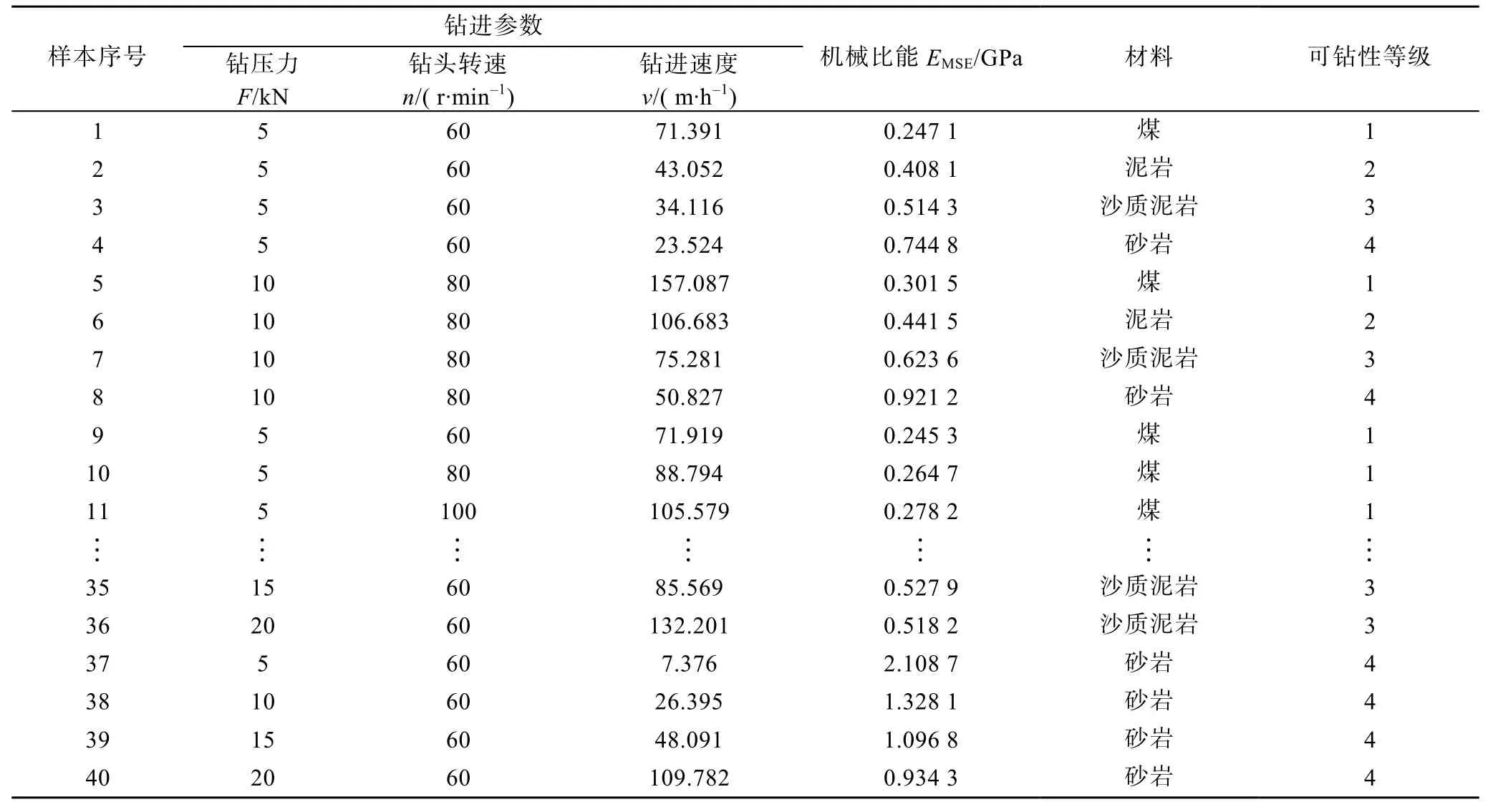
表2 部分仿真数据Table 2 Part of the simulation data

5 结论

a.当钻进参数相同时，不同材料的钻进速度和机械比能均具有较大的区分度；当钻进参数变化时，钻进速度则会出现较大的随机性，而机械比能则仍保持较高的区分度。

b.采用机械比能作为可钻性分级指标时的分级准确率高于以钻进参数作为可钻性分级指标时的分级准确率，分级结果可以为钻机调整钻进参数提供依据。

c.不同材料的机械比能随钻进参数的变化呈现出不同的规律，因此，研究机械比能与钻进参数之间的相互关系可以为优化钻进参数、提高钻孔效率提供理论指导。